基于图模型方法的Granger因果性检验∗
2016-05-25魏岳嵩
魏岳嵩
(淮北师范大学数学科学学院,安徽淮北 235000)
1 引言
由观测数据确定系统变量间的因果关系是系统辨识的重要内容.自从1969年Granger[1]提出Granger因果性概念以来,Granger因果性已经成为衡量系统变量间动态关系的重要依据,在神经网络、金融经济等众多领域都有着广泛应用[2,3].近年来,利用图模型方法研究系统变量间的Granger因果性得到了诸多学者的关注.利用图模型方法研究变量间的Granger因果性首先由Dahlhaus和Eichler[4]提出,Eichler[5,6]对其作了进一步的研究,建立了Granger因果图,并讨论了Granger因果图的Markov性.魏岳嵩等[7]给出了一种基于信息论的多维时间序列Granger因果图结构的辨识方法.本文以此为基础,进一步讨论该方法中所涉及的统计量的渐近分布及估计问题,并利用该方法分析国际主要股市之间的因果关系.
2 多维时间序列Granger因果图
设X(t)=(X1(t),X2(t),···,Xn(t))T,t∈Z,是定义在概率空间(Ω,F,P)上的n维随机过程,V={1,2,···,n}为相应的指标集.对V的任意子集A,以XA={Xa,a∈A}表示XV=X(t)的多变量子过程,(t)={X(s),s<t}表示在时刻t之前该随机过程的信息集.G=(V,Ed,Eu)表示顶点集为V的混合图,其中Ed⊆{(u,v)∈V×V|u/=v}为有向边集,而Eu⊆{(u,v)∈V×V|u/=v}为无向边集.
定义1(Granger因果性)[7]设A和B是V的不相交子集,XA和XB是XV的相应子过程,XV(t)表示在时刻t的所有有关V的信息集:
1)如果XB(t)⊥,则称XA是XB关于XV的非Granger原因(符号⊥表示独立关系);
2)如果XB(t)⊥XA(t)(t),XV{A,B}(t),则称XA和XB关于XV是非即时因果的.
定义2(Granger因果图)[7]设X(t)=(X1(t),X2(t),···,Xn(t))T,t∈Z,是定义在概率空间(Ω,F,P)上的n维平稳随机过程,如果以下条件成立,则以{X(t)}各分量序列为顶点集V={1,2,···,n}的混合图G=(V,Ed,Eu)称为Granger因果图:
1)对任意i,j∈V且i/=j,有

2)对任意i,j∈V且i/=j,有

对于以上所定义的Granger因果图G,要判断变量A和B之间是否存在相应的有向边A→B,只需判断XB(t)和关于是否条件独立,这里考虑利用信息论中的条件互信息来度量变量间的条件独立性.
设(X,Y,Z)是连续型随机向量,随机变量X的熵H(X)以及X和Y的联合熵H(X,Y)分别为

其中fX,Y(x,y)为联合概率密度,fX(x)为相应的边际概率密度函数.在已知随机变量Z的条件下,随机变量X和Y之间的条件互信息为

其中fX,Y|Z(x,y|z),fX|Z(x|z)和fY|Z(y|z)分别为相应的条件密度.
由定义易知,对于随机向量(X,Y,Z),有
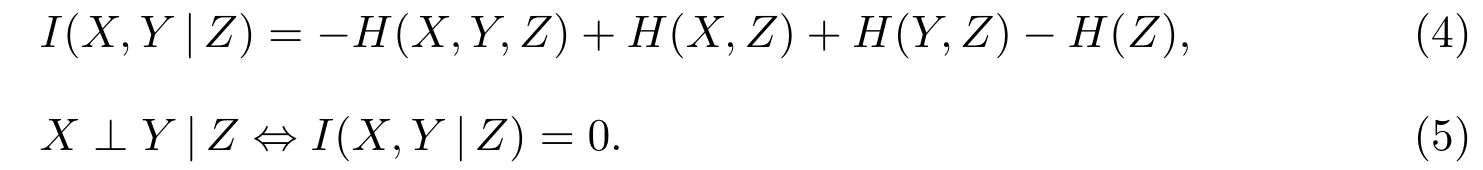
由定义2和条件互信息的定义可直接得出:
定理1若G=(V,Ed,Eu)是Granger因果图,则

定理1从理论上说明可以借助条件互信息来判断时序变量之间是否存在Granger因果关系或即时因果关系.由于条件互信息是条件独立的一个无界度量,在实际应用中设定合适的门限值相对比较困难,因此考虑条件互信息的一个变化形式.
定理2若G=(V,Ed,Eu)是Granger因果图,则
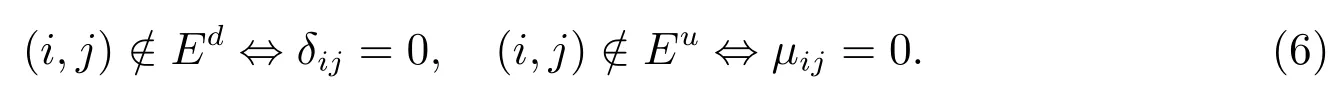
证明 由定理1及δij和µij的定义直接可得.
3 条件互信息的估计
利用信息论方法确定变量间的因果关系涉及条件互信息的估计问题.估计互信息和条件互信息的方法有很多种,如插件估计法、计算距离估计法、极大似然估计法等.当前最直接并被广泛使用的是基于对观测空间的分割来进行的非参数估计法.Butte和Kohane[8]通过由观测空间的分割所得到的直方图来估计相应的概率分布,然而该方法对于高维空间的估计效果不好.在此基础上,Daub等[9]提出了一个广义的直方图估计方法,利用B-样条函数去分配数据点到分割区间中.
本文采用非参数方法估计条件互信息.在混沌系统分析中,关联积分C(X,ε)是表征确定性过程动态特征的重要手段,它的估计相对直接.随机变量X的关联积分定义为
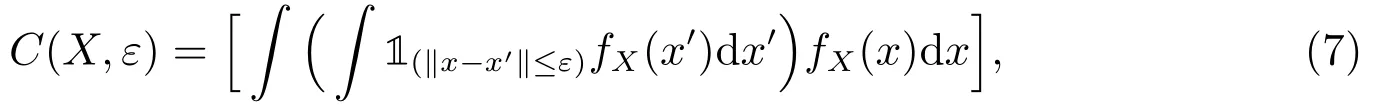
其中ε为选择的带宽,1(·)为示性函数,|是上确界范数.由于关联积分是核函数的期望值,即E(1‖X−X′‖≤ε),因此,可由U-统计量得到它的估计为

Prichard和Thdiler[10]指出:对较小的ε值,关联积分和熵之间存在关系H(X)≈−ln[C(X,ε)],因此,若以分别表示关联积分
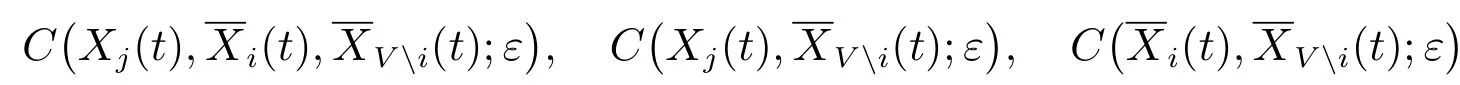
和的简写形式,以分别表示关联积分
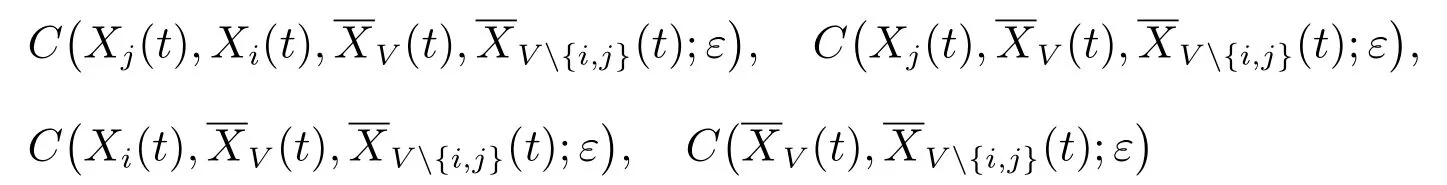
的简写形式,则相应的条件互信息估计为
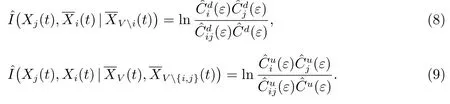
于是δij和µij的估计为

定理3设X1t,X2t,···,Xnt,t∈Z,为独立同分布序列,则δij(ϵ)和ij(ϵ)的渐近分布为
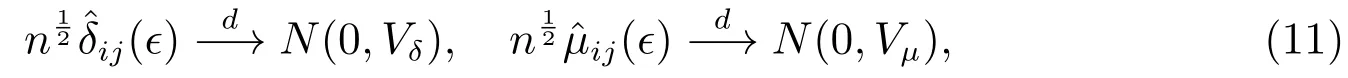
其中n为序列长度,表示依分布收敛,Vδ和Vµ为渐近方差
其中K(ε)是由下式给出的标准化因数,

证明 先证.同理可证.
对于U统计量

令

则g(ε)和都是U统计量函数.由于关联积分中核函数1(Xt,Xs)是有界的,且其值在0和1之间,满足Denker和Keller[11]中定理1的矩条件.另外,在平稳性和条件独立假设下,弱相依条件也总是满足.因此当n→∞时,分别依概率收敛到和Cd(ε),从而当n→∞时,g(ε)和δij(ε)依概率收敛到0.
令Dk,Gk,k=1,2,3,4分别表示D和G的k阶偏导数在样本值Cd(ε))上的取值.对于任意满足=0的光滑函数H,由Denker和Keller[11]定理1,将H在处泰勒展开并取极限可得

其中所有的偏导数Hi,i=1,2,3,4,在上计算,表示依分布收敛.令H分别取D和G,并记

则由式(12)有,其中

式(15)中的极限可以直接求期望得到.结合式(13)有

其中
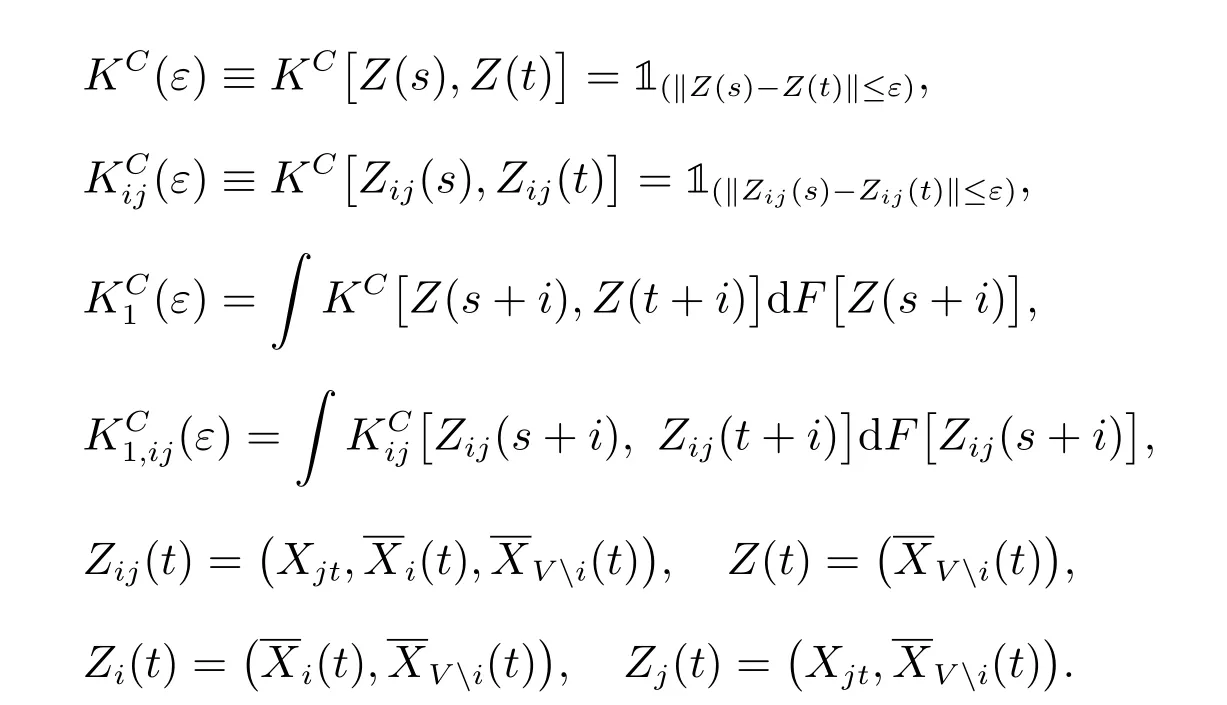
因此
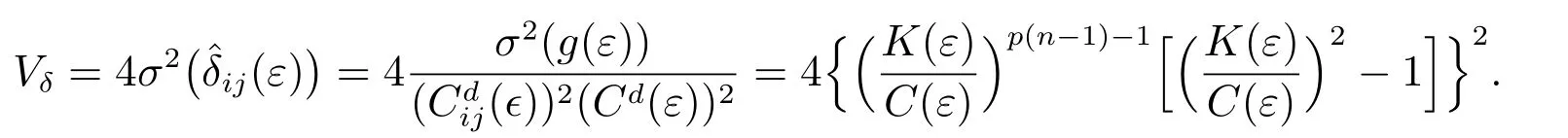
利用关联积分估计信息论变量涉及到如何选取带宽ε,这里以Gauss变量为例,分析带宽ε对估计准确性的影响.为了比较,也利用B-样条估计法估计条件互信息的大小.
假设(X,Y,Z)是零均值的三维Gauss随机变量,且分别满足以下的协方差阵
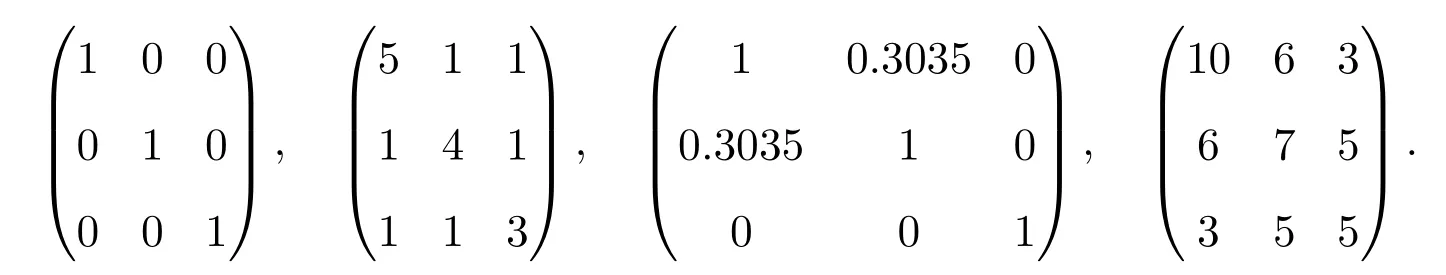
对于每一个Gauss分布,分别生成样本容量为100,200,300,400,500,1000的样本,并按上述方法计算各种样本容量下的条件互信息的估计值N(X,Y|Z).在每一种样本容量下重复进行实验1000次,在该样本容量下的条件互信息的估计值N(X,Y|Z)取其平均值.表1给出的是不同方法的估计结果.
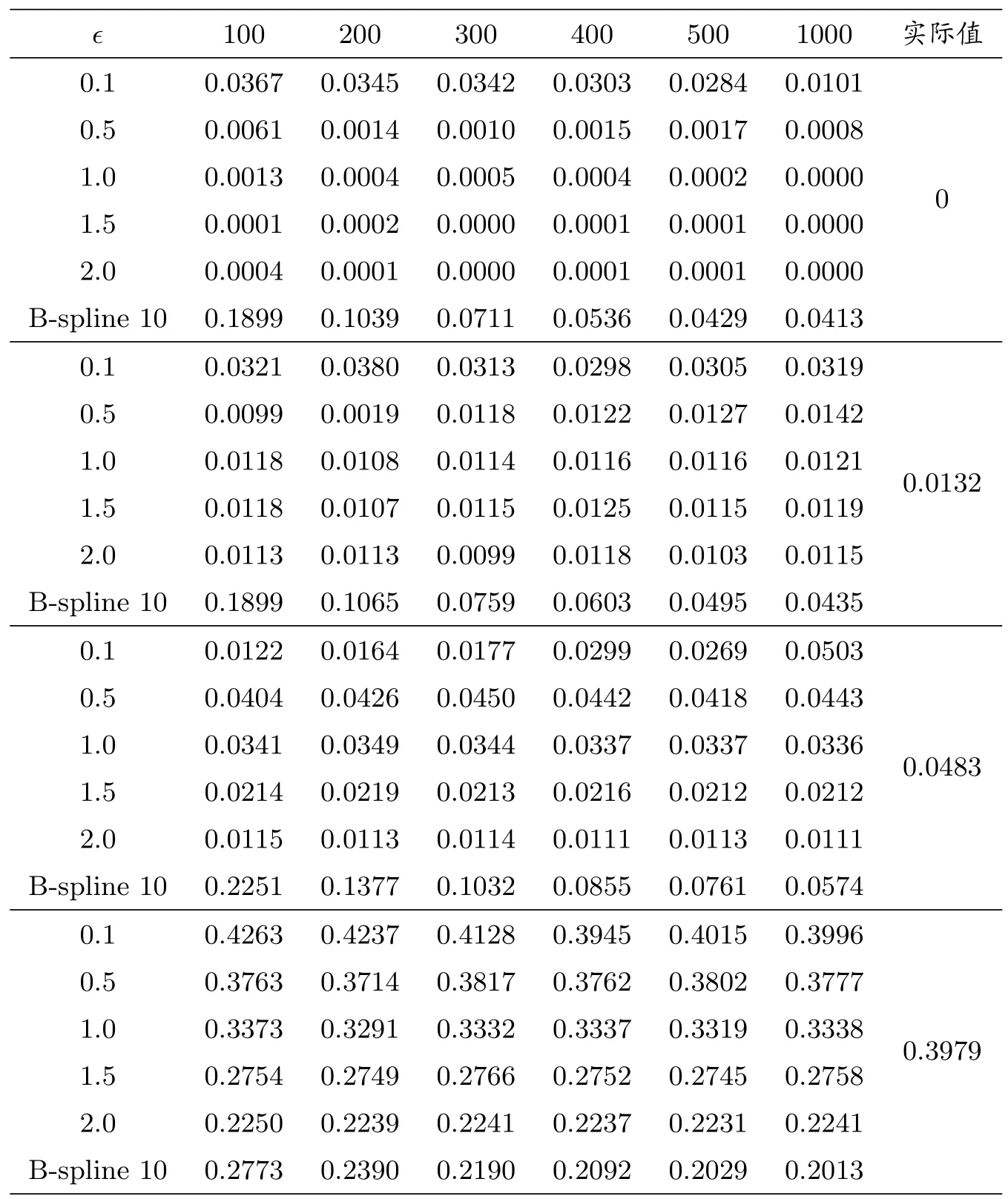
表1:选取不同带宽所得条件互信息估计值
这里在计算ˆC(·)时,事实上利用的核密度估计方法,其中使用Heaviside函数作为核函数,在实际应用中也可考虑选取其它不同的核函数,如Gauss核、多项式核函数、Epanechnikov核等.根据核方法中带宽选择的经验法则,选取了常用的几种带宽:0.1,0.5,1.0,1.5及2.0.从实验结果可以发现,即使这种比较粗略形式的核密度估计法也明显优于B-样条估计法,利用关联积分方法得到的条件互信息的估计值明显更接近于真实值.从表1中结果可以发现,整体而言,带宽选取为0.5和1.0的结果明显优于其它带宽选择所得结果.当样本量较小时,应选取较大的带宽,当样本量较大时,可适当选取较小的带宽.模拟结果显示,当带宽选取较大(如1.5和2.0)时,估计量增加负的偏差.当带宽选取较小(如0.1)时,由于样本的稀疏所造成估计量的方差较大,此时估计的结果不好.此外,随着样本容量的增加,估计值更加接近于真实值.
4 Granger因果图结构的辨识
定理3给出了估计量的极限分布,但在实际中为了避免得到统计量近似分布所需的一些复杂计算,可以利用置换检验法来判定原假设ˆδij(ϵ)=0和ˆµij(ϵ)=0是否成立.选取置换检验法也源于它的检验过程简单易行,且关联积分的估计量ˆC是次序统计量的函数,对置换后的时间序列保持相同的极限分布.该检验过程可由以下步骤形成:
步骤1计算时间序列的检验统计量,i,j∈{1,2,···,n},i/=j;
步骤2随机置换时间序列得置换序列;
步骤3计算置换序列的检验统计量;
步骤4重复步骤2和步骤3B次;
步骤5计算单边p值
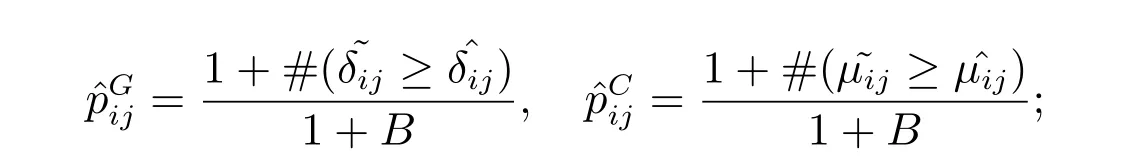
步骤6对于选定的显著性水平α,如果,则拒绝Granger非因果性的原假设;如果,则拒绝非即时因果性的原假设.
5 国际主要股市Granger因果性分析
考虑美国道琼斯工业平均指数(The Dow Jones Industrial Average,简记为DJI)、英国金融时报普通股指数(The Financial Times Ordinary Shares Index,简记为FTSE)、日经225股票指数(The Nikkei 225 Stock Index,简记为N225)、香港恒生股票指数(The Hang Seng Stock Index,简记为HSI)、上海证券交易股票指数(The Shanghai Stock Exchange Composite Index,简记为SSEC)之间的因果关系.这里使用的是2001年12月4日至2006年7月11号之间每日调整后的收盘价,数据源自雅虎金融数据库.以Pi(t),i=1,2,3,4,5,表示t日第i个股票指标的收盘价,股市收益率
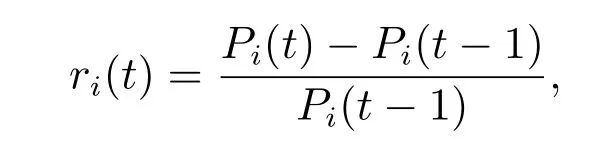
所分析的变量为r(t)=(r1(t),r2(t),r3(t),r4(t),r5(t))T.利用所给的信息论方法分析它们之间的因果关系,所得到的Granger因果图,见图1.

图1:DJI、FTSE、N225、HIS和SSEC每日收益率Granger因果图
从图1中可以得到一些有趣的结论.首先,可以发现DJI是FTSE、N225、HSI和SSEC的共同原因,这和当前对全球股市间关系—美国股市对其它股市有着深刻的影响这一常识性理解相吻合.其次,虽然SSEC受DJI、FTSE和HSI变化的直接影响,但是它仅仅对HSI产生直接影响,这说明随着中国经济的发展,中国股市和世界主要股市间的关系越来越紧密,受世界其它主要股市的直接影响也越来越大.然而,由于我国股市形成的较晚,因此它对除香港股市之外的其它股市的直接影响较小.此外,令人惊异的是,作为亚洲的主要股票市场,SSEC和N225之间不存在直接的因果关系.和SSEC相比,HSI和其它主要股票市场间的关系更加紧密,HSI对DJI、FTSE、SSEC和N225都有着直接影响,而且HSI对其它股票市场的变化也更加敏感,甚至N225的变化也对其产生直接影响,出现这种现象的主要原因可能与香港股市形成较早而且相对比较健全有关.
参考文献:
[1]Grange C.Investigating causal relations by econometric models and cross-spectral methods[J].Econometrica,1969,37(3):424-438
[2]Puente-Ajovín M,Sanso-Navarro M.Granger causality between debt and growth:evidence from OECD countries[J].International Review of Economics&Finance,2015,35(1):66-77
[3]Montalto A,Stramaglia S,Faes L,et al.Neural networks with non-uniform embedding and explicit validation phase to assess Granger causality[J].Neural Networks,2015,71(3):159-171
[4]Dahlhaus R,Eichler M.Causality and graphical models in time series analysis[C]//In Highly Structured Stochastic Systems,Oxford:University Press,2003:115-137
[5]Eichler M.Granger causality and path diagrams for multivariate time series[J].Journal of Econometrics,2007,137(2):334-353
[6]Eichler M.Graphical modelling of multivariate time series[J].Probability Theory and Related Fields,2012,153(2):233-268
[7]魏岳嵩,田铮,陈占寿.向量自回归模型Granger因果图的条件互信息辨识与应用[J].控制理论与应用,2011,28(7):979-986 Wei Y S,Tian Z,Chen Z S.Identification and application about Granger causality graph of vector autoregressive model using conditional mutual information[J].Control Theory&Application,2011,28(7):979-986
[8]Butte A J,Kohane I S.Mutual information relevance networks:functional genomic clustering using pairwise entropy measurements[J].Pacific Symposium on Biocomputing,2000,6(12):418-429
[9]Daub C O,Steuer R,Selbig J,et al.Estimating mutual information using B-spline functions-an improved similarity measure for analysing gene expression data[J].BMC Bioinformatics,2004,5(12):1-12
[10]Prichard D,Theiler J.Generalized redundancies for time series analysis[J].Physica D,1995,84(3):476-493[11]Denker M,Keller G.On U-statistics and von-Mises statistics for weakly dependent processes[J].Probability Theory&Related Fields,1983,64(4):505-522
