基于SCAD的压缩感知阈值迭代算法的收敛性分析∗
2016-05-25张会张海勾明
张 会 张 海 勾 明
(1-西北大学数学学院,西安 710069;2-中国科学院数学与系统科学研究院应用数学研究所,北京 100190)
1 引言
压缩感知[1,2]是一种全新的稀疏信号重构技术.它能在完全重建的前提下,以远小于传统的奈奎斯特采样的方式获取信息.其本质是利用信息表示的稀疏性,将采样与压缩合并进行的信息获取方式.压缩感知的意义在于突破传统的采样方式,以更经济的形式获取信息,从而为高复杂性信息的获取、处理与应用带来可能.近年来在信号处理、图像处理和统计机器学习及其它多个领域获得广泛应用[3,4].
压缩感知的数学描述为:假设有一个有限长度的信号x,x∈RN,该信号在某一下可表示为x= Ψs,这里Ψ =(θ1,θ2,···,θN),s称为基的系数,s至多有k个非零元素(k为s的稀疏度).对于此信号,通过测量矩阵Θ来对x进行观测(测量),假定得出的观测值为y,y∈Rp,即满足

通常称Φ=ΘΨ,Φ∈Rp×N为传感矩阵,当k,p,N−→∞时,
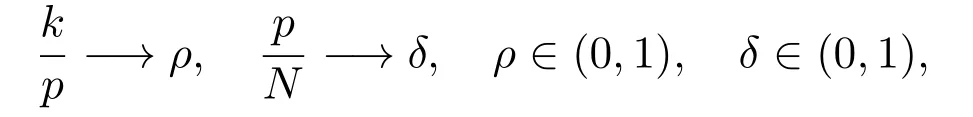
ρ是稀疏性的一种度量,δ是欠采样的比例.我们希望从观测数据y恢复稀疏未知向量s,进而恢复信号x.此问题从数学上可建模为下述L0问题个正交基

其中‖s‖0为L0范数,表示向量s的非零分量的个数.上述问题往往对应于一个NP难问题,基于此,通常将其转化为L1问题来求解

从而将一个NP难问题通过凸松弛求解.至此后,许多研究者关注于这类问题的研究[5-7],这一思想也成为当今流行的稀疏信号重建策略.
在特征提取研究中,Fan和Li[8]提出了SCAD变量选择方法,应用于高维数据处理.在统计的意义下,Fan和Li证明了SCAD具有变量选择的稀疏性,无偏性和连续性,并证明了SCAD具有好的理论性质,满足所谓的Oracle性质.因为其良好的统计性质,SCAD自提出后引起广泛关注.为研究在更少采样下信号重建工作,文献[9]将非凸的SCAD罚函数引入压缩感知问题的研究,研究表明基于SCAD的信号重建策略与现有方法相比较,在没有噪声影响时,具有很好的稀疏信号重建能力;而当有观测有噪声时,具有更好的稳健性.
经典地,求解压缩感知算法包括:OMP类算法,如OMP[10,11]、CoSaMP[12]、Subspace pursuit[13]、StOMP[14]、ROMP[15]等;重迭代算法,如The reweightedl1-minimization[16]、IRLS[17,18]等.OMP类算法主要用于求解问题(2),此类算法在信号稀疏度比较大时收敛速度很快.重迭代算法主要用于求解问题(3).OMP类算法是一种阈值迭代算法,阈值迭代算法可以高效、快速、精确求解压缩感知问题.因此,对阈值迭代算法的研究很有价值.文献[19]分析了凸阈值迭代算法以及非凸阈值迭代算法的收敛性.我们在文献[9]给出了高效的阈值迭代算法,但未给出其收敛性分析.本文是文献[9]工作的延续,基于SCAD的压缩感知阈值迭代算法,从理论上分析其收敛性,给出其收敛到稀疏解的充分条件,并证明其收敛速率达到指数阶.
进一步,众所周知,在稀疏信号重建问题中,稀疏性与欠采样的权衡很重要,快速迭代算法是解决稀疏信号重建问题的一种算法,但是该算法在稀疏性与欠采样的权衡方面效果很差,不能完全重建稀疏信号.Donoho等人[20]研究发现,基于逼近Belief Propagation算法改进的AMP算法的时间复杂度远远低于Belief Propagation算法,同时通过实验验证了基于AMP改进的Soft阈值迭代算法在稀疏性与欠采样的权衡方面较原阈值迭代算法有很大的改善,新方法在稀疏性与欠采样的平衡方面与凸优化相当,估计稀疏向量能力有很大的提高.为进一步提高SCAD阈值迭代算法重建稀疏信号的能力,本文研究基于AMP改进的SCAD阈值迭代算法,给出基于AMP改进的SCAD阈值迭代算法,并证明其收敛性.
2 基于SCAD的压缩感知阈值迭代算法
本节首先给出基于SCAD的压缩感知阈值迭代算法.对于一个有限长度的信号x∗,s∗为x∗在正交基下的系数,Φ为传感矩阵,基于SCAD的压缩感知的数学模型为

其中

我们在文献[9]中给出了SCAD阈值函数的形式,SCAD阈值迭代算法可表示为
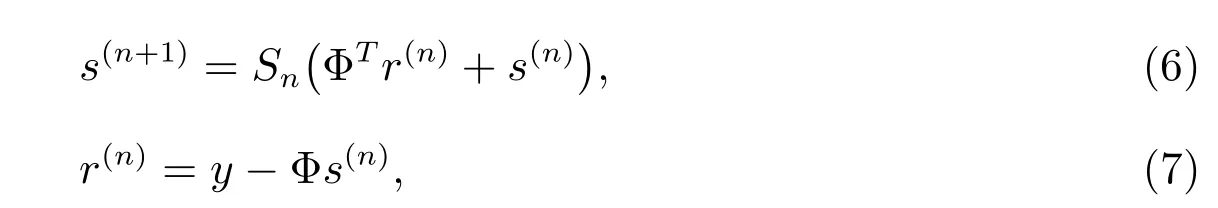
这里Sn(·)是SCAD阈值函数,s(n)是第n次迭代的估计值,r(n)是第n次迭代的残差,ΦT是Φ的转置.
记ϕi为Φ的第i列向量,s(i)为s的第i个元素,J为指标集.定义

s(i)的主动集(若s的元素s(j)通过阈值,则把s(j)放入集合I中(即j∈I),集合I就称为主动集)记为I(i),s∗的主动集记为I∗,k为s∗的稀疏度(即s∗至多有k个非零的元素).Φ的相关性记为
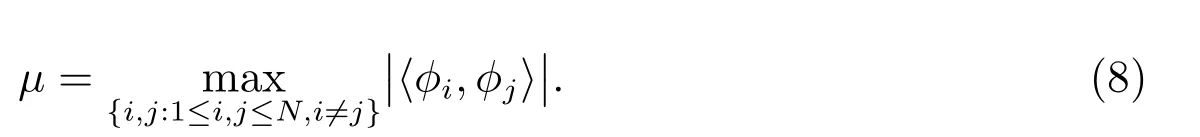
定理1假定,且对任意的1≤i<k,都有

成立,则SCAD阈值迭代算法至多需要步就能恢复重建稀疏信号s∗,并且当t≥L时,有

且对任意的j,有
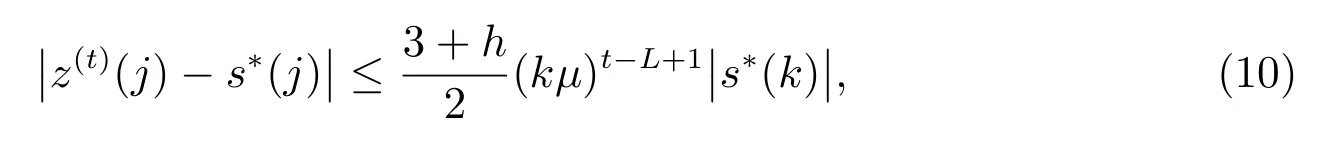
其中

这里c为大于零的常数.
注1稀疏信号s∗的稀疏度k通常不会很大,传感矩阵Φ的相关性µ的大小可以控制,因此,假定是可行的.
注2定理1表明SCAD阈值迭代算法只需有限步就可以找到正确的主动集,并且SCAD阈值迭代算法一旦找到正确的主动集,就能以指数阶的速率收敛到精确解.
3 定理1的证明
本节给出定理1的证明.记

这里s∗是最优值,s(i)是第i步的估计值,z(i+1),w(i)的第j个元素记为z(i+1)(j),w(i)(j),不失一般性,我们假设s∗的元素按绝对值大小递减排列(即s∗的前k个元素非零,且|s∗(1)|≥|s∗(2)|≥···≥|s∗(k)|≥0),迭代初始值选为s(0)=0.为了证明定理1,我们需要以下三个引理.
引理1假定,则s∗的最大元素s∗(1)在第1步迭代后进入主动集中,并且对任意的j,有

证明

上式第三个等式成立是由于我们假设迭代初始值为零(即s(0)(j)=0),则就有I(0)为空集,上式第四个不等式成立是由于当j∈I∗I(0)时,w(0)(j)=s∗(j),且有|s∗(j)|≤|s∗(1)|.这里我们只考虑s∗的最大元素s∗(1)在第1步迭代后是否进入主动集中,对于1<i≤k不做讨论.当i>k时,有

由于假设,所以有kµ<1−kµ,故
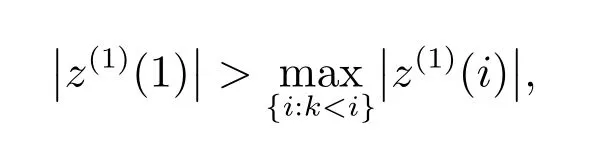
因此,s∗的最大元素s∗(1)在第1步迭代后进入主动集中,并且有
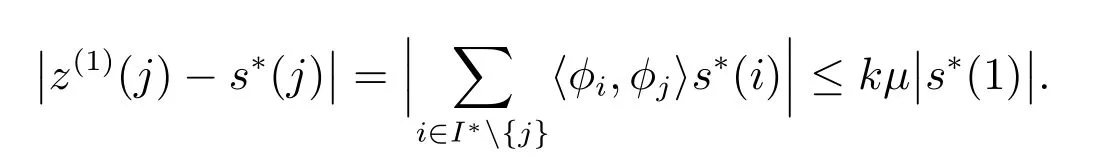
引理2假定当r<k时,在第m步迭代后s∗(1),s∗(2),···,s∗(r)都在主动集中,并且对任意的j,有

如果,则在第m+n步迭代后,s∗(1),s∗(2),···,s∗(r)仍在主动集中,并且对任意的j,有

证明 我们用数学归纳法证明这个引理,首先证明,当n=1时结论成立.

上式第二个不等式成立是由于当j∈I(m)时,w(m)(j)=s∗(j)−z(m)(j),我们假定当r<k时,在第m步迭代后s∗(1),s∗(2),···,s∗(r)都在主动集中,即{1,2,···,r}⊂I(m),故当j∈I∗I(m)时,w(m)(j)=s∗(j),并且|s∗(j)|≤|s∗(r+1)|.下面我们将证明s∗的前r个元素在主动集中.当i∈{1,2,···,r}时
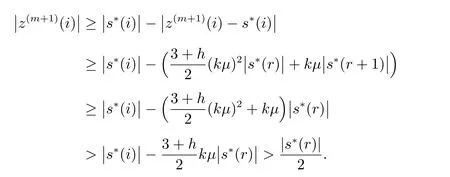
上式第四个不等式成立是由于有下面事实成立,令fs=α+α2+···+αs+βαs+1,若β(1−α)>1,则对任意的s有fs<βα成立,取s=1即可得到第四个不等式.当i>k时

因此,s∗的前r个元素在主动集中.从而n=1时结论成立.
接下来,我们假定第m+n步迭代结论成立,证明第m+n+1步迭代结论成立,与n=1时证明过程类似有

易得
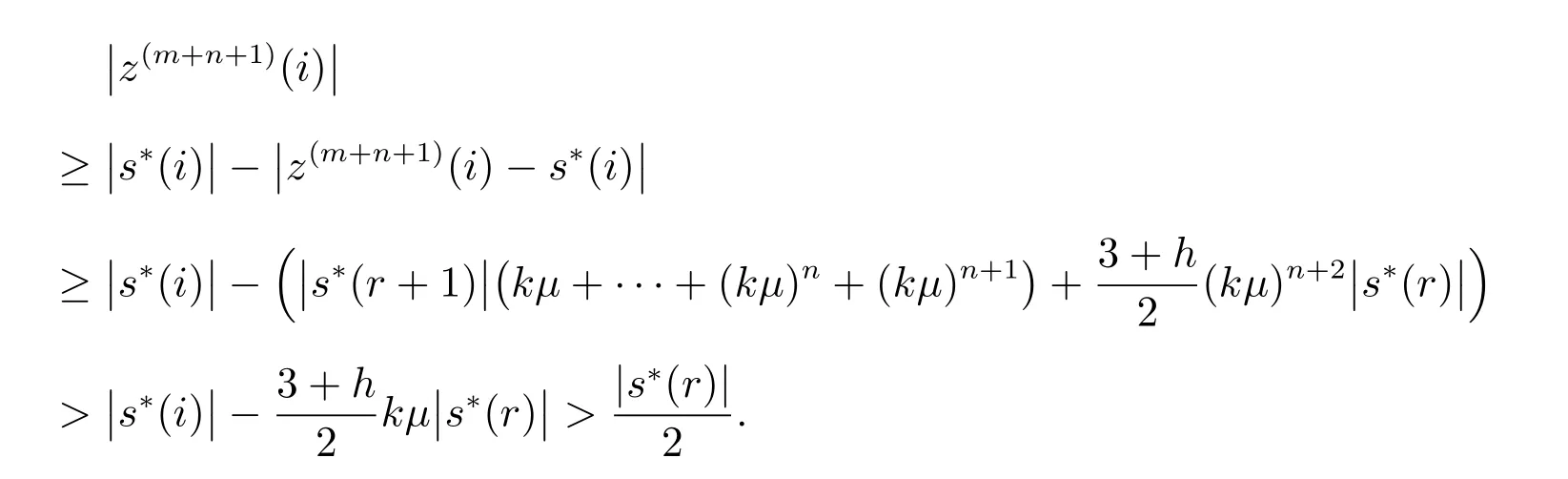
当i>k时
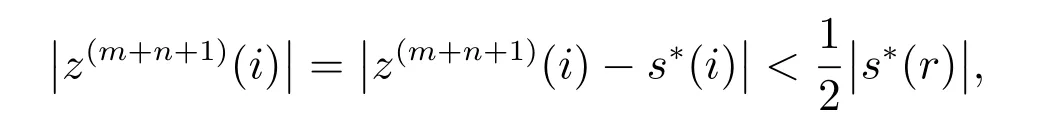
由于

因此,s∗的前r个元素在主动集中,从而第m+n+1步迭代结论成立.
引理3假定,当r<k时
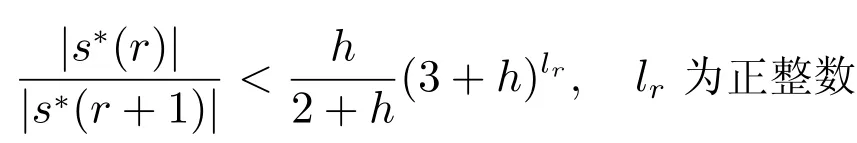
成立,并且在第m步迭代后s∗(1),s∗(2),···,s∗(r)都在主动集中,如果对任意的j,有

那么,再经过lr步迭代后,s∗(r+1)将进入主动集中,并且对任意的j,有

证明 令n=lr,由引理2可得
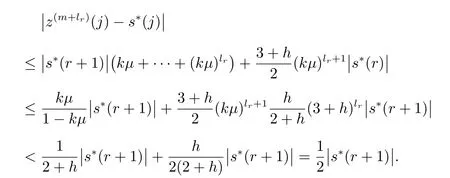
同引理2证明,得
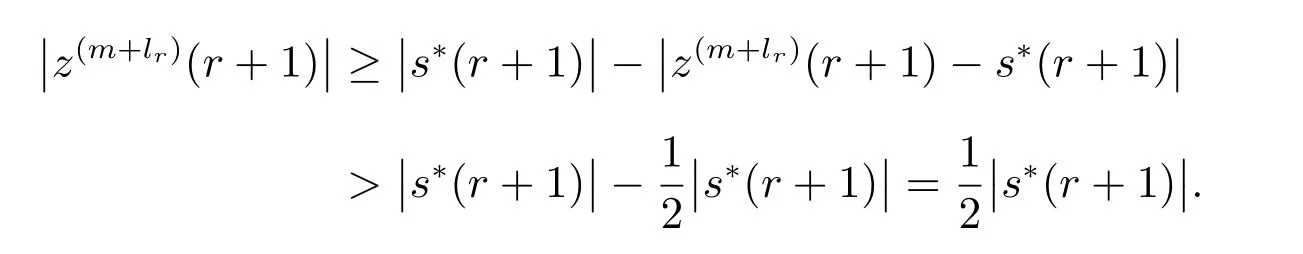
当i>k时

由于
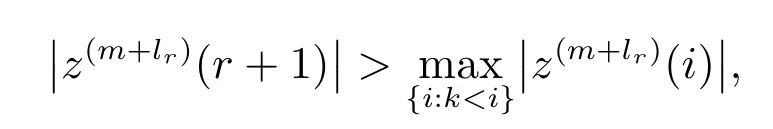
所以在第m+lr步迭代后,s∗(r+1)在主动集中.下面我们给出算法的误差界,对任意的j,有
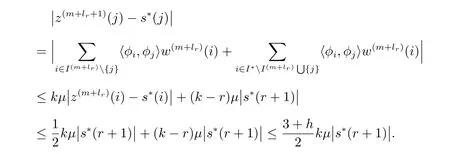
定理1的证明我们仍采用数学归纳法证明.由引理1、引理2、引理3得,当迭代步数i=1时,由引理1可知s∗的最大元素被找到,假定s∗(1),s∗(2),···,s∗(r)在主动集中,则由引理2可知这些元素将会一直在主动集中,由引理3我们知道经过lr步迭代后,s∗(r+1)将进入主动集中,并且再多迭代一步,估计值的每个元素与最优值的误差界小于

这个过程可以重复进行,故SCAD阈值迭代算法至多需要步就能恢复重建稀疏信号s∗.最后,我们证明当s∗的所有元素在主动集中时,迭代估计值与最优值的误差以指数阶的速率趋于零,证明如下,我们假定在第m步迭代后s∗(1),s∗(2),···,s∗(k)都在主动集中,并且对任意的j,有

如果,则在第m+n步迭代后s∗(1),s∗(2),···,s∗(k)仍在主动集中,并且对任意的j,有

与引理2类似,我们采用数学归纳法证明.假设第m+n步迭代结论成立,即在第m+n步迭代后s∗(1),s∗(2),···,s∗(k)仍在主动集中(即I∗⊂I(m+n)),并且对任意的j,有
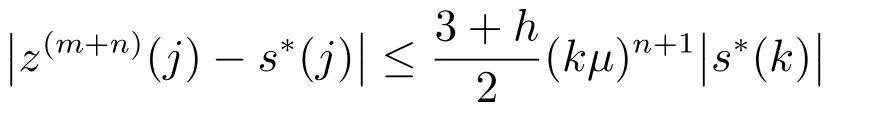
成立,那么在第m+n+1步迭代后,由引理2可知s∗(1),s∗(2),···,s∗(k)仍在主动集中,并且对任意的j,我们有
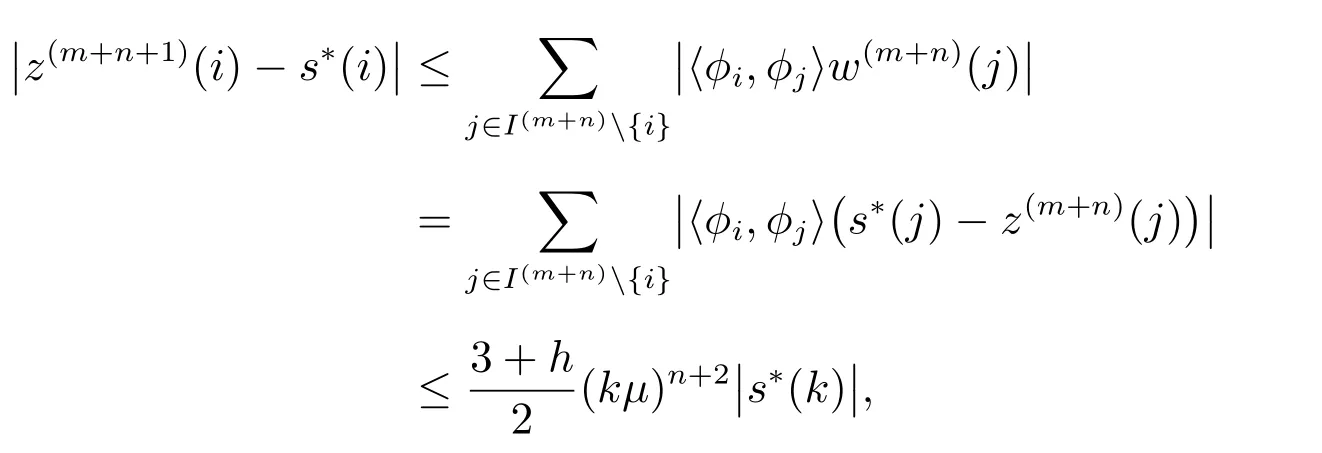
故第m+n+1步迭代结论成立,从而结论成立.我们知道经过L步迭代后s∗(1),s∗(2),···,s∗(k)都在主动集中,故取m=L,m+n=t,则可以得到

从而定理得证.
4 基于AMP改进的SCAD阈值迭代算法
如引言所述,迭代算法能够快速求解稀疏信号重建问题,但是该算法在稀疏性与欠采样的权衡方面效果很差,不能完全重建稀疏信号,SCAD阈值迭代算法也存在这方面不足.为进一步提高SCAD阈值迭代算法重建稀疏信号的能力,本文研究基于AMP改进的SCAD阈值迭代算法.本节首先给出基于AMP改进的SCAD阈值迭代算法,然后对其算法收敛性开展研究.
给定初始值s(0)=0,基于AMP改进的SCAD阈值迭代算法可表示为

这里,对于一个向量
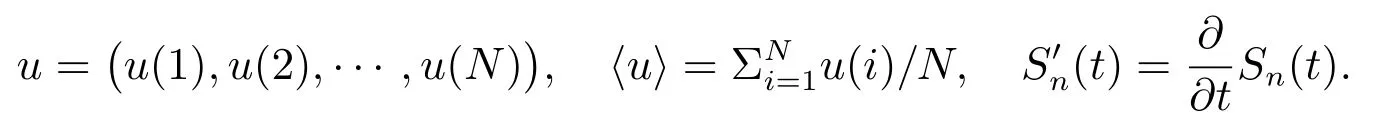
从而可得
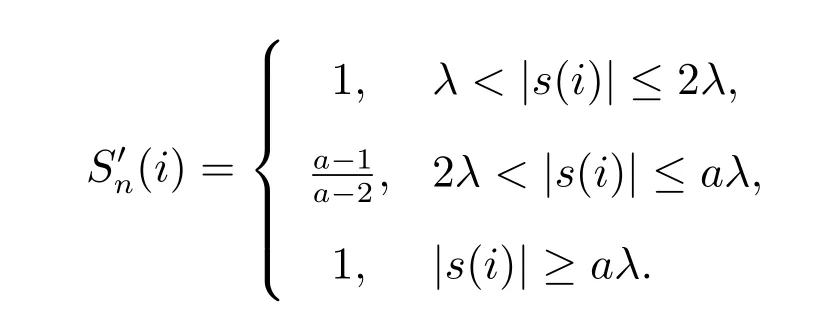
对于不可导的点,以该点的次导数作为其导数,所以

记

一般情况下,k远小于p,所以e<1.
定理2假定kµ<ε(ε为正数),且对任意的1≤i<k,都有

成立,则基于AMP改进的SCAD阈值迭代算法至多需要+1步(li为正整数)就能恢复重建稀疏信号s∗,并且当t≥L时,有

且对任意的j,有

注3定理2表明基于AMP改进的SCAD阈值迭代算法只需有限步就可以找到正确的主动集,并且迭代估计值与真实值的误差有界.
5 定理2的证明
本节给出定理2的证明.首先,记

为了证明定理2,我们需要以下几个引理.
基于AMP改进的SCAD阈值迭代算法与SCAD阈值迭代算法第一步迭代相同,所以由引理1可得若,则s∗的最大元素s∗(1)在第1步迭代后进入主动集中,并且对任意的j,有

引理4假定,则在第n+1歩迭代后,s∗(1)仍在主动集中,并且对任意的j,有

证明 我们用数学归纳法证明这个引理,首先证明当n=1时结论成立.

令ε(1)1=,若ε1≤ε(1)1,则
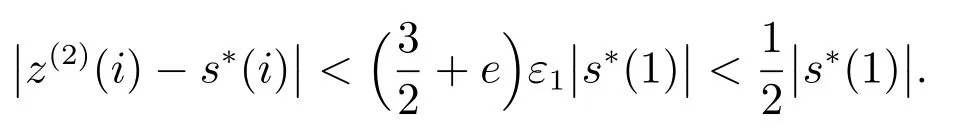
下面我们将证明s∗的第1个元素仍在主动集中.当i=1时

当i>k时

由于

因此,s∗的第1个元素仍在主动集中.从而n=1时结论成立.
接下来,我们假定n<t时结论成立,证明n=t时结论成立,与n=1时证明过程类似,我们有

由于e<1,所以存在,令

若ε1≤ε(t)1,则

易得

当i>k时
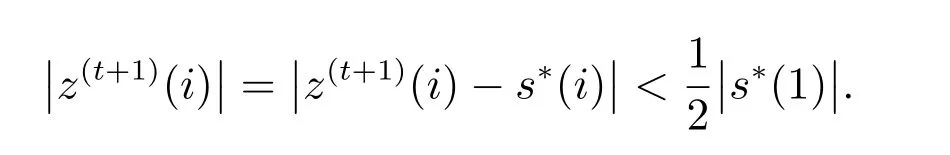
由于
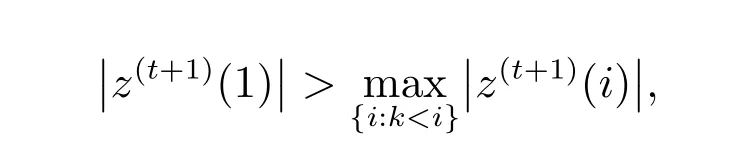
因此,s∗的第1个元素仍在主动集中,从而第t+1步迭代结论成立.令
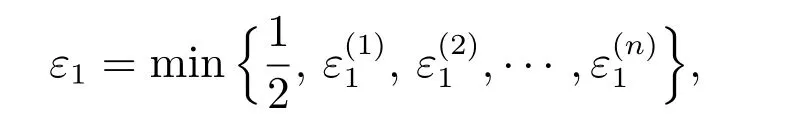
引理结论成立.
引理5假定

成立,那么再经过l1步迭代后,s∗(2)将进入主动集中,并且对任意的j,有

证明令n=l1,由引理4可得

同引理4证明,得
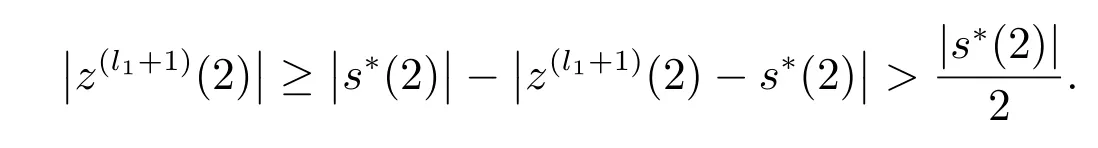
当i>k时

由于

因此,s∗的第2个元素在主动集中,并且对任意的j,有

令

可得若kµ<ε(1)2,则对任意的j,有

从而引理成立.
引理6假定kµ<ε2≤ε(1)2,则在第l1+n+1歩迭代后,s∗(1),s∗(2)仍在主动集中,并且对任意的j,有

证明 我们用数学归纳法证明这个引理,首先当n=1时,由引理5的证明可得,若kµ<ε(1)
2,则有

下面我们将证明s∗的第2个元素仍在主动集中.当i=2时
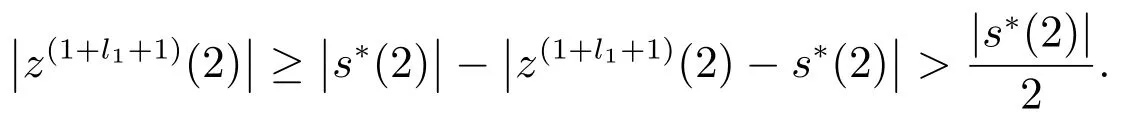
当i>k时

由于

因此,s∗的第2个元素仍在主动集中.从而n=1时结论成立.
接下来,我们假定n<t时结论成立,证明n=t时结论成立,与n=1时证明过程类似,有

令

若ε2≤ε(t)2,则
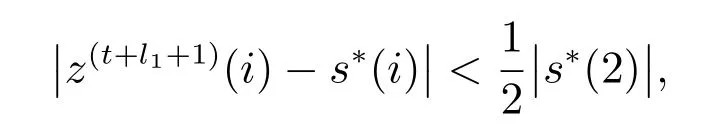
易得

当i>k时

由于

因此,s∗的第2个元素仍在主动集中,从而第t+l1+1步迭代结论成立.令ε2=,引理结论成立.
引理7假定
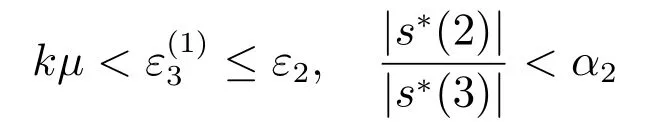
成立,那么再经过l2步迭代后,s∗(3)将进入主动集中,并且对任意的j,有

证明 令n=l2,由引理6可得

令
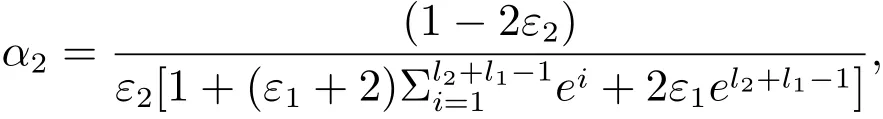
可得

同引理6证明,得

当i>k时
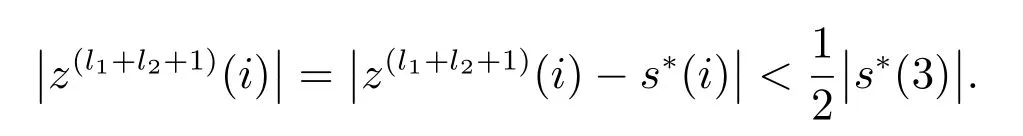
由于

因此,s∗的第3个元素在主动集中,并且对任意的j,有

可得若kµ<ε(1)3,则对任意的j,有

从而引理成立.
定理2的证明由引理4、引理5、引理6、引理7,依此类推可以得到ε1,ε2,···,εk(ε1≥ε2≥···≥εk),α1,α2,···,αk−1,以及l1,l2,···,lk−1.若ε≤εk,则当kµ<ε(ε为正数),且对任意的
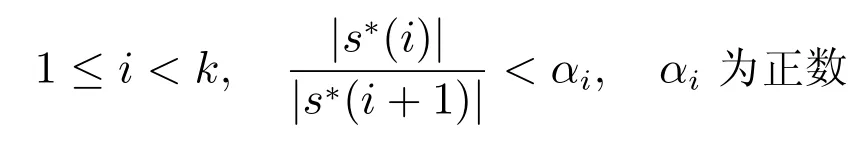
成立时,基于AMP改进的SCAD阈值迭代算法至多需要步(li为正整数)就能恢复重建稀疏信号s∗,并且当t≥L时,令就有I∗⊂I(t),且对任意的j,有

从而定理得证.
6 结论
压缩感知是一种全新的稀疏信号重构技术,其本质是利用信息表示的稀疏性,将采样与压缩合并进行的信息获取方式,开展其快速重建算法研究有着重要的意义.阈值迭代算法是一种高效、快速、重建精度高的求解压缩感知问题的算法.基于非凸罚函数的压缩感知是近期研究热点之一.本文研究基于SCAD罚函数的阈值迭代算法的收敛性,证明了在信号稀疏度和传感矩阵的相关性满足一定条件的情况下,SCAD阈值迭代算法至多需要有限步就能精确重建稀疏信号,并且一旦找到精确解,其迭代估计值与最优值的误差以指数阶的速率趋于零.从而从理论上为基于SCAD罚函数的阈值迭代算法提供了支撑.由于快速迭代算法在稀疏性与欠采样的权衡方面效果很差,而AMP算法在稀疏性与欠采样的权衡方面有很大的改善,重建稀疏信号能力有很大的提高.因此,本文研究基于AMP改进的SCAD阈值迭代算法,并证明其收敛性.本文结果可推广到其它非凸阈值迭代算法.
参考文献:
[1]Candes E,Romberg J,Tao T.Stable signal recovery from incomplete and inaccurate measurements[J].Communications on Pure and Applied Mathematics,2006,59(8):1207-1223
[2]Donoho D.Compressed sensing[J].IEEE Transactions on Information Theory,2006,52(4):1289-1306
[3]Euder H G.On compressive sensing applied to radar[J].Signal Processing,2010,90(5):1402-1414
[4]Majumdar A,Ward K.Compressed sensing of color images[J].Signal Processing,2010,90(12):3122-3127[5]Chen S,Donoho D,Saunders M.Atomic decomposition by basis pursuit[J].SIAM Journal on Scientific Computing,1998,20(1):33-61
[6]Tibshirani R.Regression shrinkage and selection via the lasso[J].Journal of the Royal Statistical Society,1996,58(1):267-288
[7]Xu Z B,Zhang H,Wang Y,et al.Lregularizer[J].Science in China:Information Sciences,2010,53(6):1159-1169
[8]Fan J Q,Li R Z.Statistical chanllenges with high dimensionality:feature selection in knowledge discovery[OL].arXiv preprint math/0602133,2006
[9]张海,梁勇,徐宗本,等.基于SCAD罚函数的有噪压缩感知集[J].数学学报,2013,56(5):767-776 Zhang H,Liang Y,Xu Z B,et al.Compressive sensing with noise based on SCAD penalty[J].Acta Mathematica Sinica,2013,56(5):767-776
[10]Pati Y,Rezaifar R,Krishnaprasad P.Orthogonal matching pursuit:recursive function approximation with application to wavelet decomposition[C]//Signals,Systems and Computers,1993,1993 Conference Record of the Twenty-Seventh Asilomar Conference on IEEE,1993:40-44
[11]Tropp J,Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2007,53(12):4655-4666
[12]Needell D,Tropp J A.CoSaMP:iterative signal recovery from incomplete and inaccurate samples[J].Applied and Computational Harmonic Analysis,2008,26(3):301-321
[13]Dai W,Milenkovic O.Subspace pursuit for compressive sensing signal reconstruction[J].IEEE Transactions on Information Theory,2009,55(5):2230-2249
[14]Donoho D L,Tsaig Y,Drori I,et al.Sparse solution of underdetermined systems of linear equations by stagewise orthogonal matching pursuit[J].IEEE Transactions on Information Theory,2012,58(2):1094-1121
[15]Needell D,Vershynin R.Signal recovery from incomplete and inaccurate measurements via regularized orthogonal matching pursuit[J].IEEE Journal of Selected Topics in Signal Processing,2010,4(2):310-316[16]Candes E,Wakin M B,Boyd S.Enhancing sparsity by reweightedL1minimization[J].Journal of Fourier Analysis and Applications,2008,14(5):877-905
[17]Gorodnitsky I F,Rao B D.Sparse signal reconstruction from limited data using FOCUSS:a reweighted minimum norm algorithm[J].IEEE Transaction on Signal Processing,1997,45(3):600-616
[18]Daubechies I,Devore R,Fornasier M,et al.Iteratively reweighted least squares minimization for sparse recovery[J].Communications on Pure and Applied Mathematics,2010,63(1):1-38
[19]Zeng J S,Lin S B,Xu Z B.Sparse solution of underdetermined linear equation via adaptively iterative thresholding[J].Signal Processing,2014,97:152-161
[20]Donoho D L,Maleki A,Montanari A.Message passing algorithms for compressed sensing[J].Proceedings of the National Academy of Sciences,2009,106(45):18914-18919
