A Balanced Finite Element Method of Least-squares Formulation for Singularly Perturbed Reaction-diffusion Problems∗

QIU Chang-xin,ZHAO Wei-jia,SONG Li-na

(School of Mathematics and Statistics,Qingdao University,Qingdao 266071)

1 Introduction

Consider the singulary perturbed linear reaction-diffusion problem

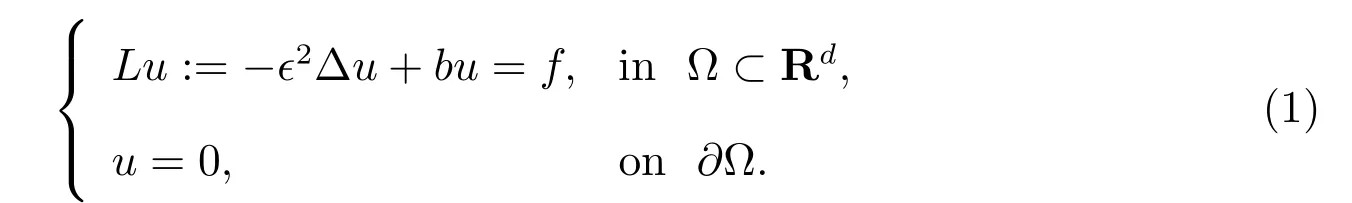
The domain Ω is bounded with(whend≥2)Lipschitz-continuous boundary∂Ω,and the parameterϵsatisfies 0＜ϵ≪1.candfare continuous functions in,0＜b0≤b≤b1in¯Ω with two positive constantsb0andb1.

It is well known that exact solutions to singular perturbation problems(1)typically contain layers,which cause nonmonotonic numerical oscillation in the solutions by using the standard Galerkin finite element methods(FEMs).The least-squares finite element method(LSFEM)is a general methodology,which is based on the minimization of the residuals in a least-squares sense.Continuous and discontinuous LSFEMs have been applied to solve convection-reaction-diffusion problems[1-7].Recently,from[8],the author proposed a discontinuously discretized LSFEM for 1D singularly perturbed reaction-diffusion problems with constant coefficients.

The singularly perturbed problem(1)has attracted much attraction in the literature.The properties of its solutionuare discussed in[9,10],where it is shown that typicallyuexhibits sharp boundary layers near the boundary∂Ω of Ω.Define the energy norm

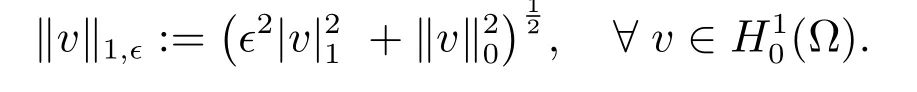
For smallϵ,the energy norm is a weak norm because it is essentially no stronger than theL2(Ω)norm when applied to the type of solution typically encountered in this singularly perturbed problem[11].

In this paper,we consider a new stronger norm first introduced by[11],

where 0＜b0≤b≤b1inand the two positive constantsb0andb1are the lower and upper constants bound of reaction coefficientb,respectively.Based on the new norm,we propose the LSFEM for singularly perturbed reaction-diffusion problems in 1D spaces.Moreover,we prove the stability of the method and analyze its error estimation.The numerical examples verify the theoretical results that the new norm‖|v|‖ϵworks better than‖v‖1,ϵ.In this paper,we can see the comparison of the error estimate by the two norms while the convergency of the two norms are almost the same.But we can not see the comparison in[11].

The paper is organized as follows.Section 2 introduces definitions and notations used in this paper.In section 3,we present the singularly perturbed problem and construct its least-squares variational formulation.We prove coercivity of the bilinear forms in the associated new stronger norm constructed by[11].In section 4,a priori error estimate results are presented in one dimension.In section 5,numerical examples are given,whose verify the theoretical results.

2 Notations

Throughout this paper,we shall useCto denote a generic positive constant which is independent ofϵand of any mesh;it can take different values at different places.Vectors and scalars are denoted by bold and plain letters,respectively.Fork≥0 we writeHk(Ω)for the usual Sobolev space,soH0(Ω)=L2(Ω).And the associated seminorm and norm are denoted by|·|and‖·‖l.LetH10(Ω)denote the space of functions inH1(Ω)whose traces vanish on∂Ω.TheL2(Ω)inner product is denoted by(·,·);and ifv=(v1,v2,···,vn)andw=(w1,w2,···,wn),then.Similarly,we set

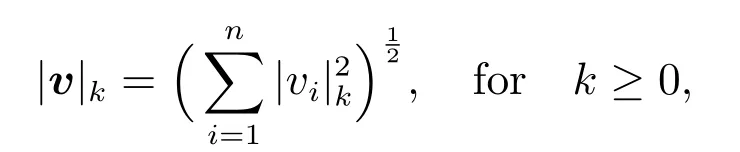
and the‖v‖kdefined likewise.Let

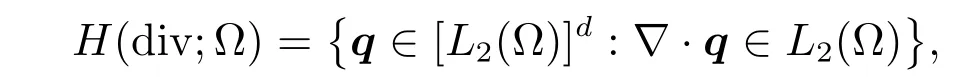
andH(Ω)=H(div;Ω)×H10(Ω).So the associated norms are like this

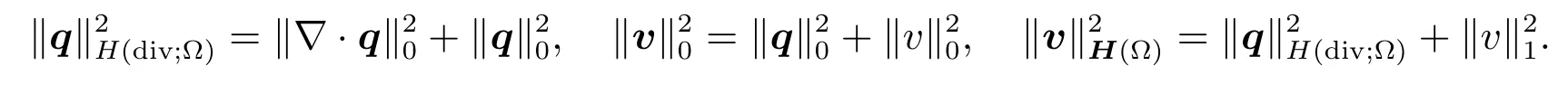
In this paper,the vector-valued functionsu,v,w,andfinH(Ω)have components

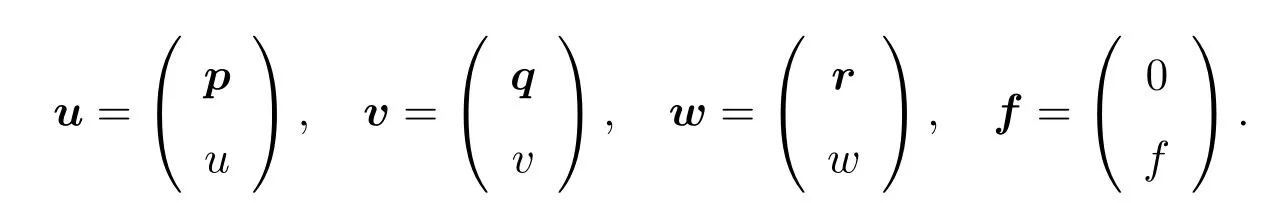
Herep,q,r,0 are vector functions that each hasdcomponents.

3 The least-squares finite element approximations by the balanced norm

Let us write(1)as the following system of first-order equations

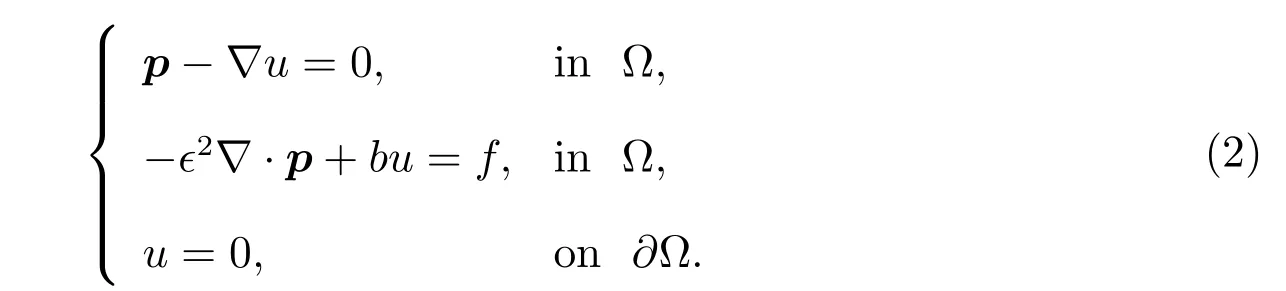
Foru∈H(Ω),define

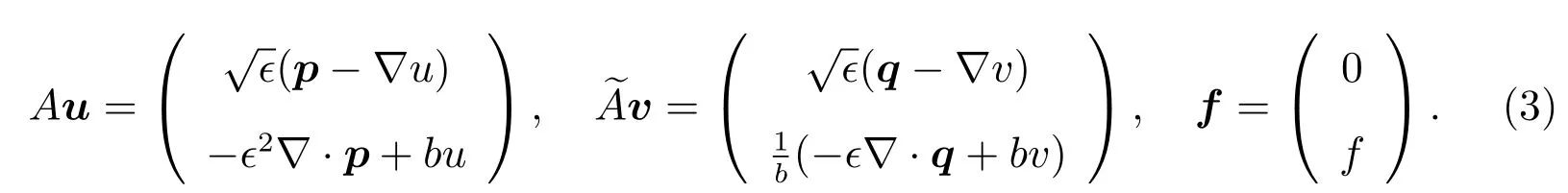
Then the problem(1)is equivalent to the first-order system

Consider the least-squares functionalJinH(Ω)defined by

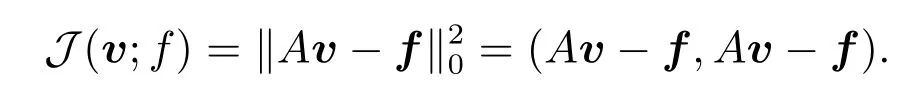
The least-squares method findsu∈H(Ω)such that

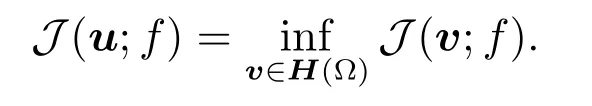
From[1],we can find the necessary condition foruto be a minimizer of the functionalJis that its first variation vanishes atu,i.e.,

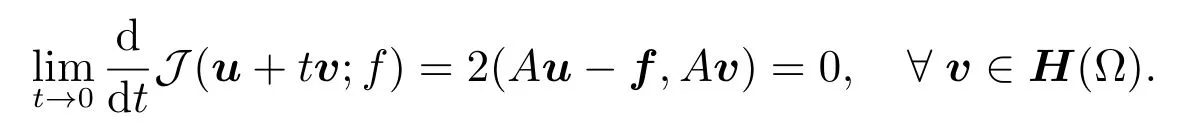
The corresponding least-squares variational formulation for problem(1)thus follows:fi ndu∈H(Ω)such that

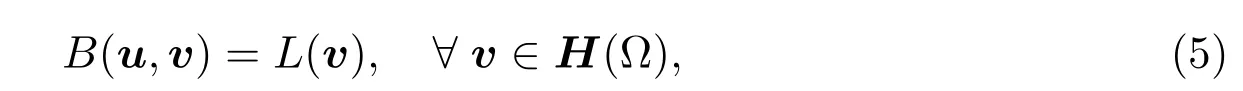
where the bilinear formB:H(Ω)×H(Ω)→ℜ,the linear functionalL:H(Ω)→ℜare defined by

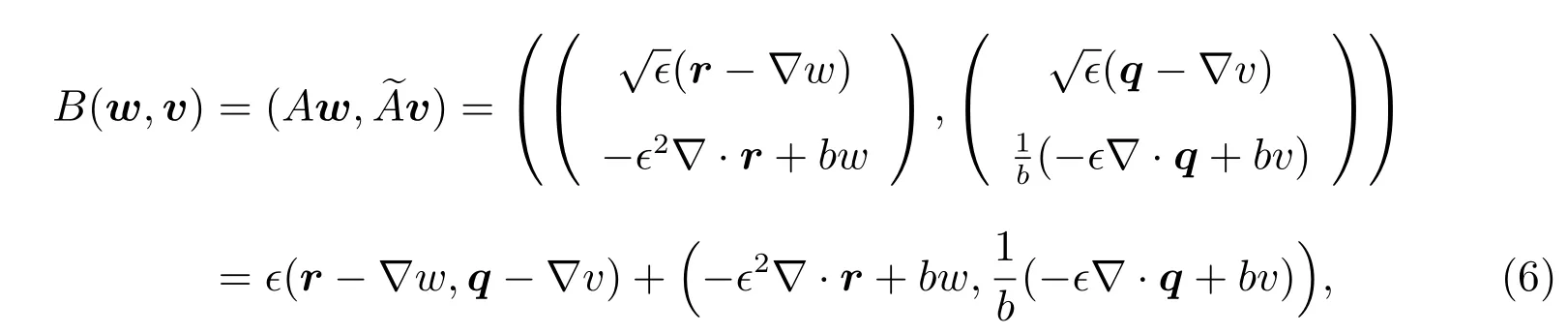
and

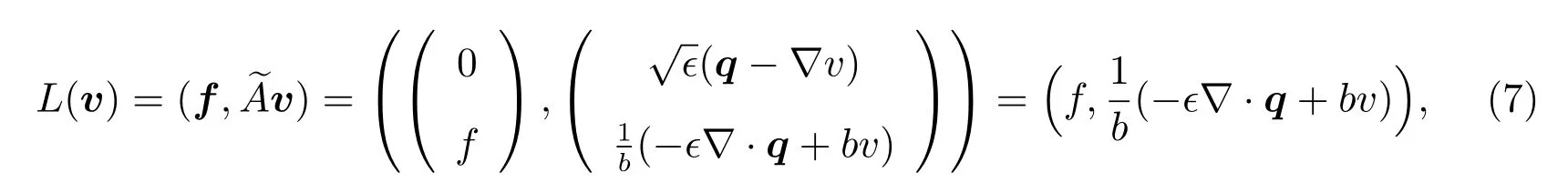
respectively.The new norm is defined as follows

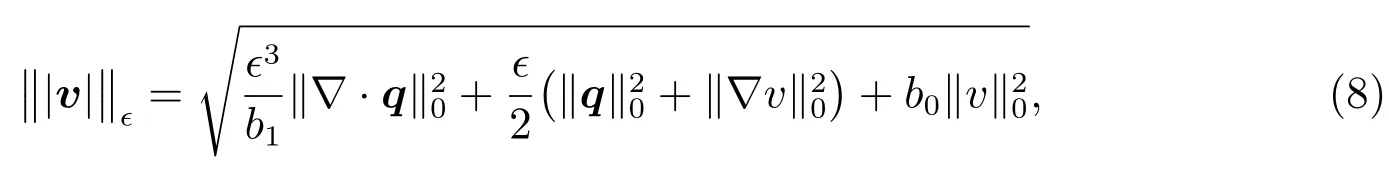
where 0＜b0≤b≤b1inwith two positive constantsb0andb1.If the solutionuof(1)has typical boundary layers and is otherwise well-behaved,then on puttingv=uandq=∇uin(8),each term on the right-hand side isO(1),so the new norm‖|v|‖ϵis balanced,unlike the energy norm‖·‖1,ϵ.Furthermore‖|v|‖ϵis stronger than the energy norm.In addition,we have the following boundedness and coercivity results.

Theorem 1(boundedness and coercivity ofB(·,·)with respect to‖|v|‖ϵ)There exists a positive constantC1,which is independent ofϵ,such that

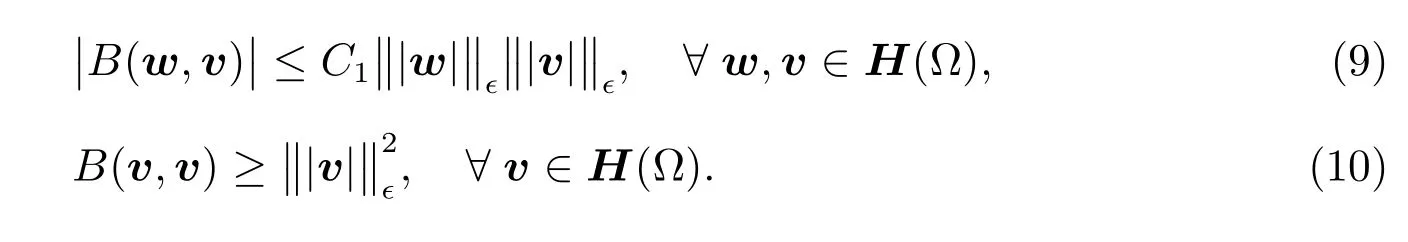
ProofTo derive(9),letw=(r,w)andv=(q,v)∈H(Ω)be arbitrary.Then

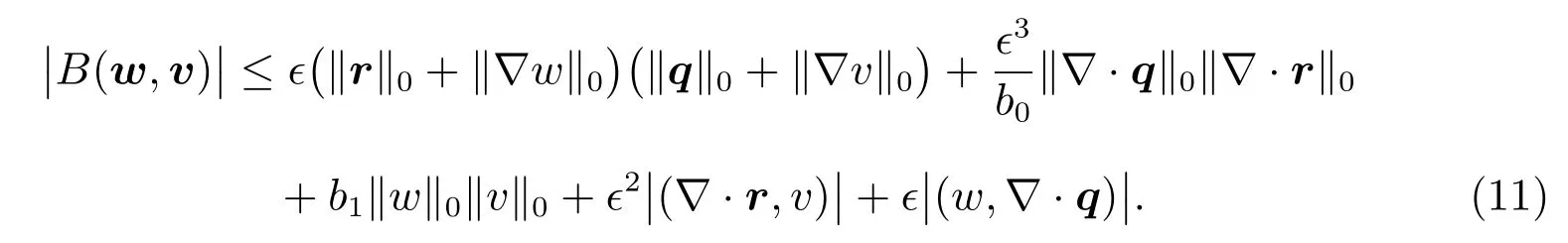
Integrating by parts gives

Combine(11)and(12),and refer to the(8),we can get

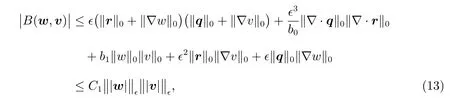
for some constantC1which is independent ofϵ.

Now we prove the coercivity(10):Letv=(q,v)T,so we have

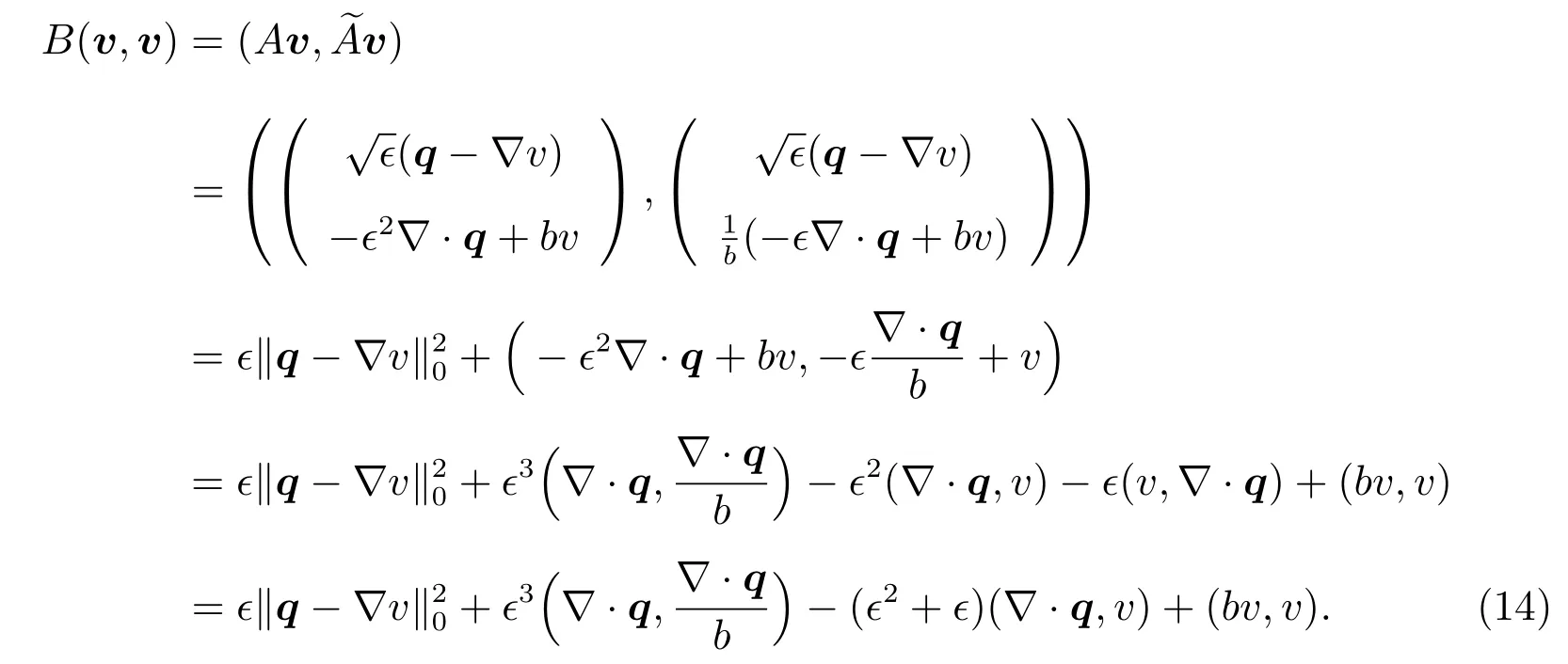
Asv∈H10(Ω),integration by parts gives

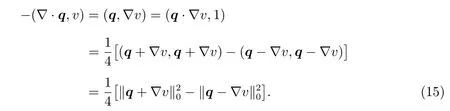
Combine the(14)and(15),we obtain

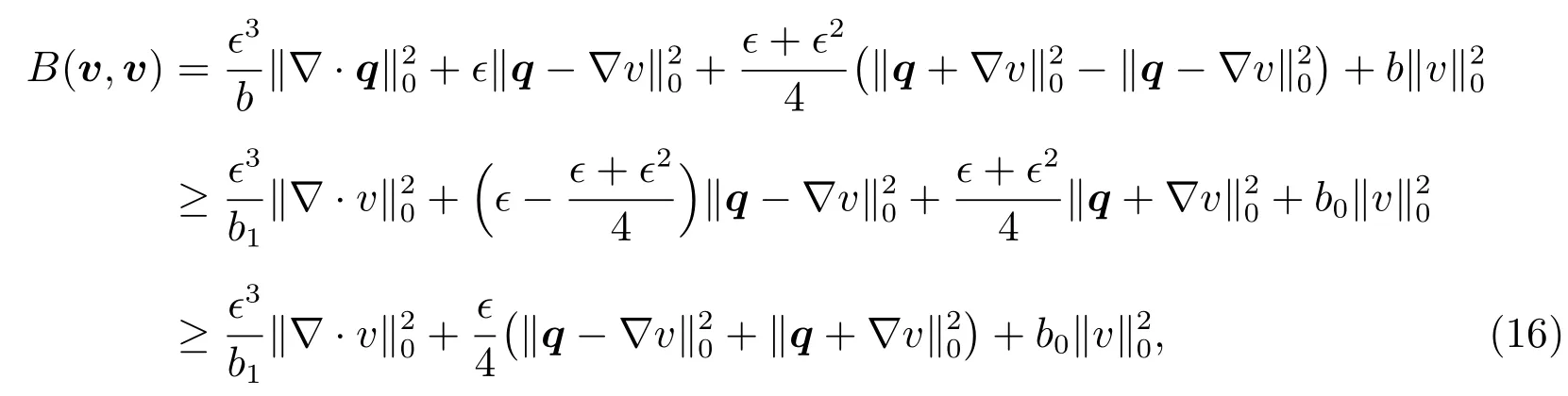
where we used 0＜ϵ2≤ϵ≤1.Since

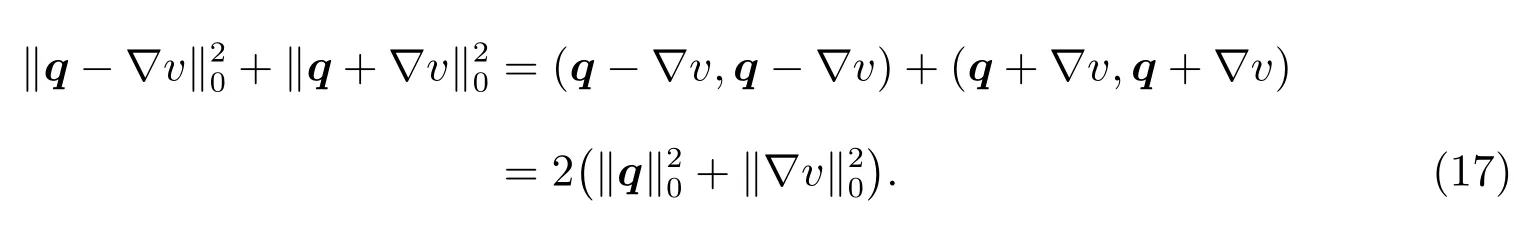
Then,we have

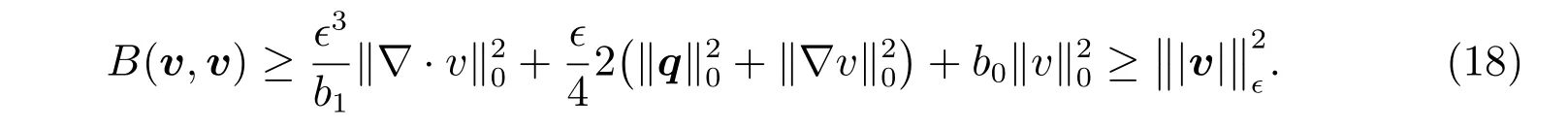
SoB(v,v)≥‖|v|‖2ϵ,as desired.

4 Error estimates

In this section,we present some a priori error estimate results.LetVh⊂H(Ω)be any finite element space.We get the approximation for the least-squares variational formulation(5)as follows.Finduh=(ph,uh)T∈Vhsuch that

where

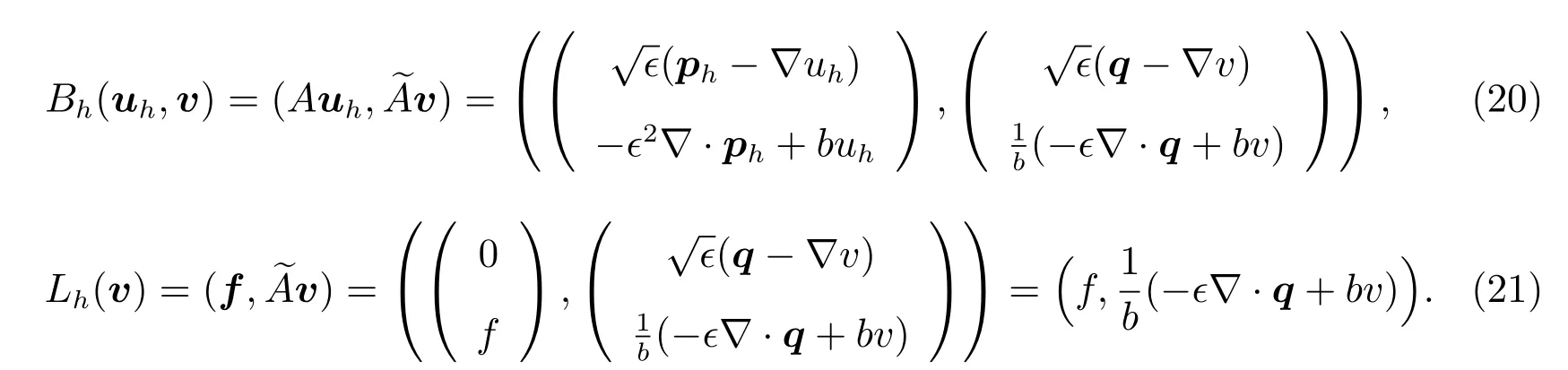
Proposition 1The bilinear formBh(·,·)defined by(19)is consistent.

ProofRefer to Proposition 4.1 in[1].

Letuanduhbe the solution to the problems(5)and(19),respectively.It follows from Proposition 1 that theBh(·,·)satisfies the Galerkin orthogonality

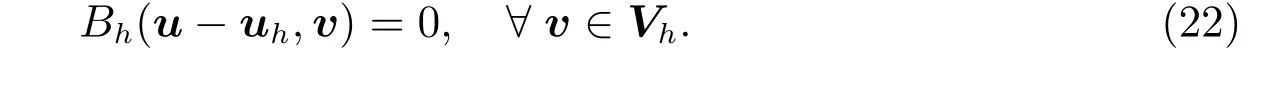
Then by Theorem 1 and Proposition 1,we have

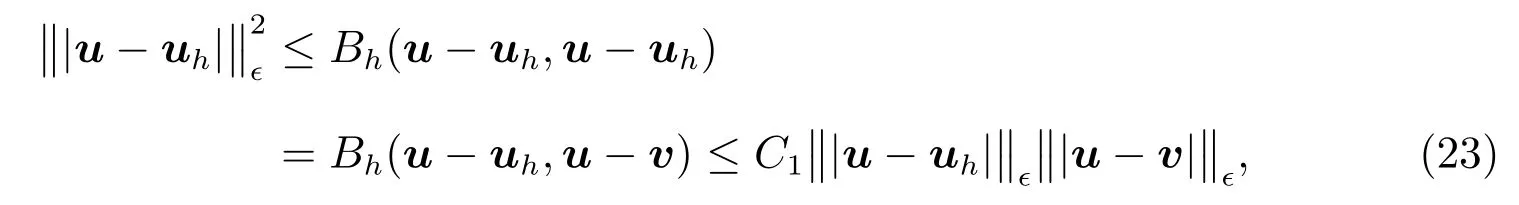
for allv∈Vh,which implies the following estimate.

Theorem 2Letuanduhbe the solution to(5)and(19),respectively.Assume that the conditions of Theorem 1 are fulfilled.Then

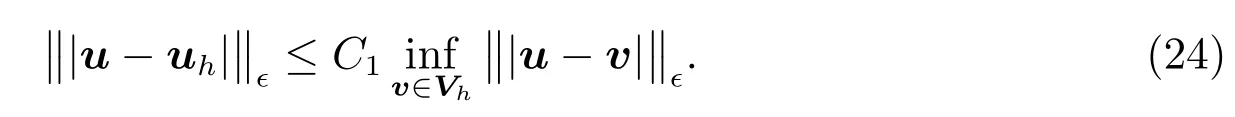
Thus the approximation to the least-squares variational formulation is optimal in theϵ-dependent norm.Consequently,we get the following priori error estimate.

Theorem 3Letuanduhbe the solution to(5)and(19),respectively.Assume thatu∈H3(Ω)and the conditions of Theorem 1 are fulfilled.Then

whereNis the number of the mesh intervals in each coordinate direction.

ProofLetIhuandIhpbe the standard linear or bilinear finite element interpolation ofuandp(i.e.,∇u),respectively.So

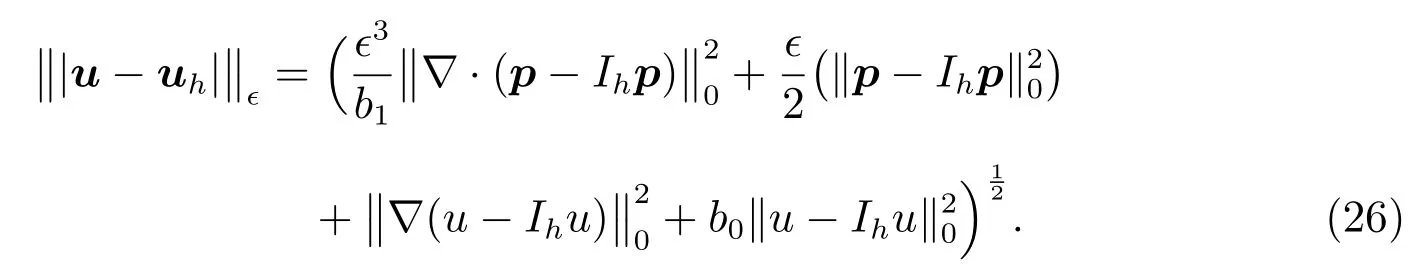
In the equation,we can get

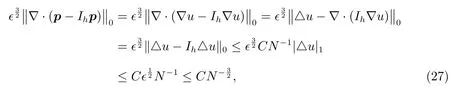
where we used the Corollary 4.6 andϵ≤CN−1in the(4.3a)of the[11].

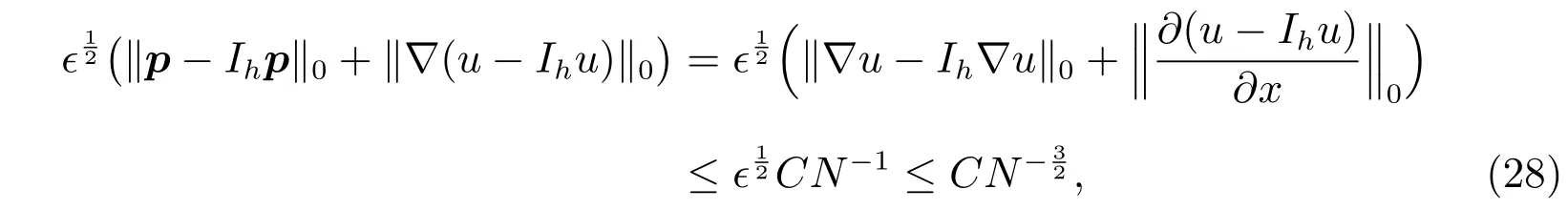
where we used the Lemma 4.4,Lemma 4.2 andϵ≤CN−1in the(4.3a)of the[11].Also by the Lemma 4.3 of the[1],we get that there exists a constantCsuch that

Combine the(26)—(29),we can get what we desired.

5 Numerical experiments

In this section,we present a numerical example to illustrate the theoretical results of the developed method in section 3.High order Gaussian quadrature rules are used to calculate the norms of numerical errors over the computational regions(including the layers),which hereby cause no competitive extra errors in numerical integration.In the following example,consider the singularly perturbed reaction-diffusion problem

The analytical solution to(30)is

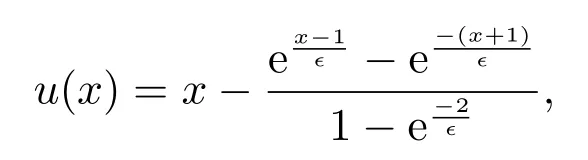
which has a typical exponential boundary layer atx=1 whenϵ≪1.

In Figure 1,we present the numerical results of LSFEM.All numerical computations are conducted in uniform meshes withh=.This shows the smaller withh,the closer to analytical solution.Finally,Table 1 and Table 2 are used to test for numerical independence of the LSFEM method onϵ.It is observed that when a singular perturbation occurs,the numerical results of Table 1 for the energy norm‖u−uh‖1,ϵhas the convergence of order.The numerical results of Table 2 for the balanced norm‖|u−uh|‖ϵshow the convergence of order,which agrees with Theorem 2.For comparison,we find the order of convergence of Table 1 and Table 2 are almost the same,but the errors in‖|·|‖ϵnorm are obviously less than those in‖·‖1,ϵnorm.

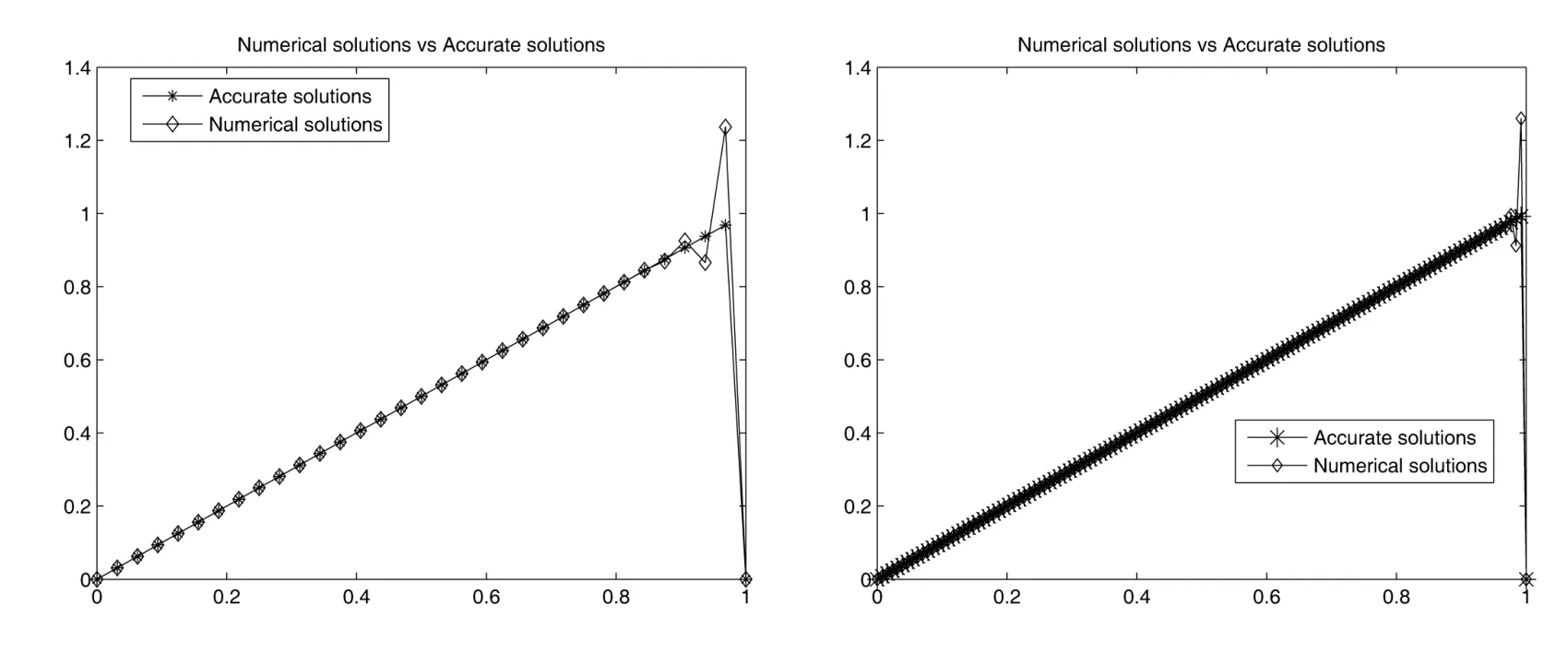
Figure 1: From left to right:with ϵ2=10−8

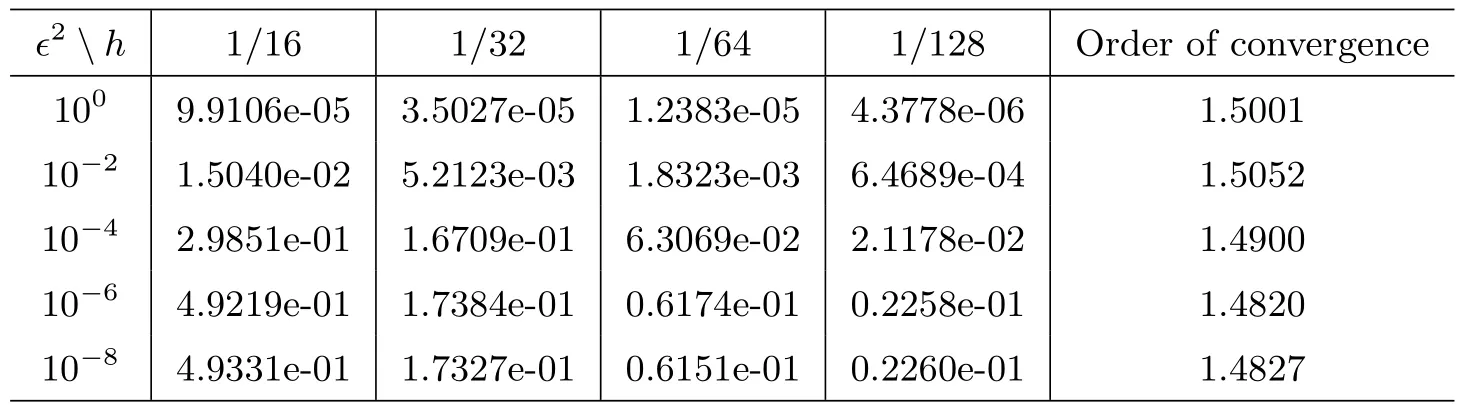
Table 1: Numerical errors ‖u − uh‖1,ϵ

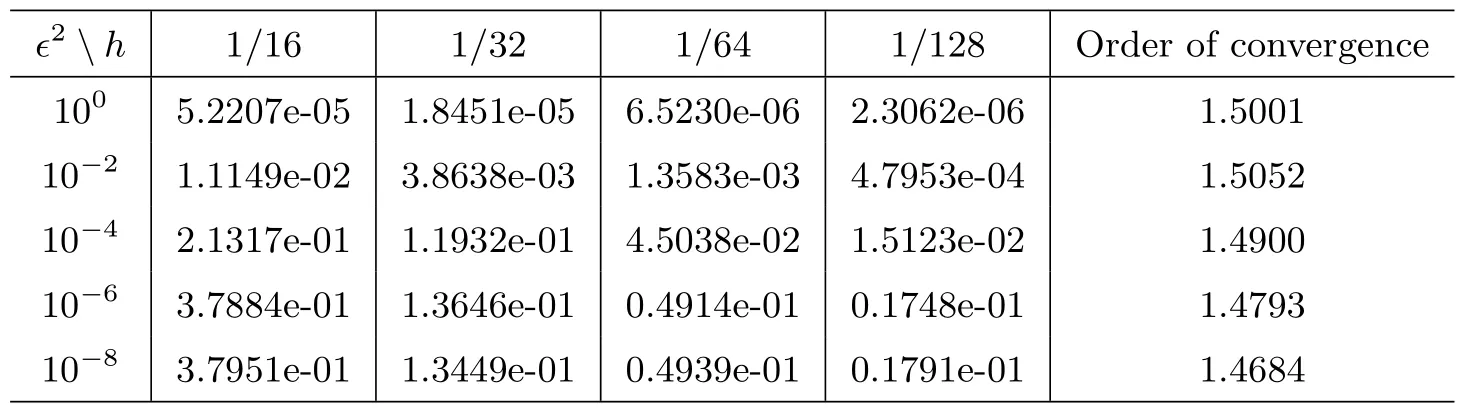
Table 2: Numerical errors ‖|u − uh|‖ϵ

6 Conclusion

In this paper,we showed that the balanced norm is stronger and is moreover balanced than the standard energy norm,because the energy norm is essentially the same as theL2norm for singularly perturbed reaction-diffusion problems.Theoretical convergence results(with respect to the balanced norm)were proved for this finite element method on 1D mesh.Numerical results were presented to agree with these theoretical bounds in the balanced norm.

References:

[1]Lin R C.Discontinuous discretization for least-squares formulation of singularly perturbed reaction-diffusion problems in one and two dimensions[J].SIAM Journal on Numerical Analysis,2008,47(1):89-108

[2]Bochev P B.Least-squares finite element methods for first-order elliptic systems[J].International Journal of Numerical Analysis and Modeling,2004,1(1):49-64

[3]Bochev P,Gunzburger M.On least-squares finite element methods for the Poisson equation and their connection to the Dirichlet and Kelvin principles[J].SIAM Journal on Numerical Analysis,2005,43(1):340-362

[4]Bramble J H,Lazarov R D,Pasciak J E.Least-squares for second-order elliptic problems[J].Computer Methods in Applied Mechanics and Engineering,1998,152(1-2):195-210

[5]Cai Z,Lazarov R,Manteuffel T A,et al.First-order system least squares for second-order partial differential equations:part I[J].SIAM Journal on Numerical Analysis,1994,31(6):1785-1799

[6]Cai Z Q,Manteuffel T A,McCormick S F.First-order system least squares for second-order partial differential equations:part II[J].SIAM Journal on Numerical Analysis,1997,34(2):425-454

[7]Carey G F,Shen Y.Least-squares finite element approximation of Fisher’s reaction-diffusion equation[J].Numerical Methods for Partial Differential Equations,1995,11(2):175-186

[8]Lin R C.A discontinuous least-squares finite element method for singularly perturbed reaction-diffusion problems[C]//Dynamics of Continuous,Discrete and Impulsive Systems,SeriesA,Mathematical Analysis,2007,14(supp1.S2):243-246

[9]Zhang Z M.Finite element superconvergence approximation for one-dimensional singularly perturbed problems[J].Numerical Methods for Partial Differential Equations,2002,18(3):374-395

[10]Clavero C,Gracia J L,O’Riordan E.A parameter robust numerical method for a two dimensional reactiondiffusion problem[J].Mathematics of Computation,2005,74(252):1743-1758

[11]Lin R C,Stynes M.A balanced finite element method for singularly perturbed reaction-diffusion problems[J].SIAM Journal on Numerical Analysis,2012,50(5):2729-2743