无轴承异步电动机解耦控制策略研究现状

孙宇新，钱忠波

(江苏大学，镇江 212013)

无轴承异步电动机解耦控制策略研究现状

孙宇新，钱忠波

(江苏大学，镇江 212013)

由于轴承与转子之间不存在摩擦力，无轴承异步电动机(bearingless induction motor, BIM)不添加润滑油就能实现高速旋转，且具有工作噪声低和振动低等优点，在电气传动领域极其重要的科研与应用价值。但是BIM中电磁关系十分复杂，必须对其进行解耦控制。首先对BIM的工作原理及其数学模型进行分析，其次综述了BIM在解耦控制策略方面的研究现状，同时提出了相关关键问题优化改进的研究发展方向。

无轴承异步电动机; 工作原理; 数学模型; 解耦控制方法; 研究发展方向

0 引 言

由于无轴承电动机应用电磁作用产生磁拉力使得轴承与转子之间隔离，则不需要添加润滑油就能实现高速旋转，它磨损损耗小，维护方便并且具有低噪声和低振动等特点，因而在电气传动领域有着极其重要的科研与应用价值。参考目前已发表文献可知，传统的电动机都可以采用类似方法实现无轴承技术[1]。这些电机中，无轴承异步电动机(以下简称BIM)是最具研究价值的无轴承电动机之一[2]。但是电机内部电磁关系极其错综复杂，因此对BIM进行动态解耦控制是实现转子稳定悬浮，同时也是实现电动机无级调速运行的首要问题。

针对以上问题，本文首先对BIM的工作原理和数学模型进行了简单阐述和分析，然后总结了国内外无轴承异步电机解耦控制相关的关键技术，并提出相应的研究发展方向。

1 BIM工作运行机理

图1为BIM的内部结构示意图。从结构上对BIM进行分析可知，通过在原有的定子绕组中添加一套悬浮力绕组，转矩绕组在内侧一圈且极对数为1，由U，V，W三相绕组组成，每相绕组有4个线圈，其作用为产生电磁转矩，使电机旋转；悬浮力绕组在外侧一圈，极对数为2，用来产生径向悬浮力。这两套绕组的极对数相差1且电角频率相同。两套不同极对数绕组磁场发生相互作用，使原有对称的气隙合成磁场发生改变，在转子上能够产生可控制的径向磁拉力，最终实现转子在稳定悬浮同时能够无级调速。

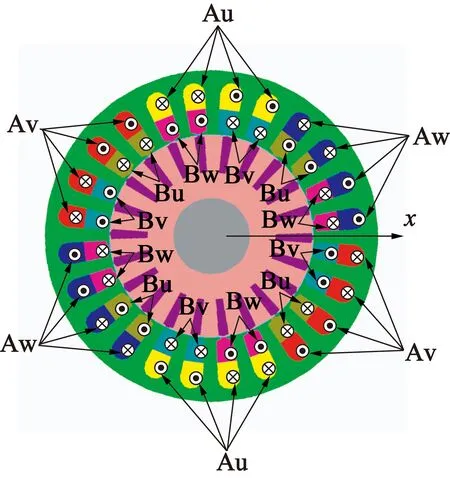
图1 BIM内部结构示意图

在加入悬浮绕组后，电动机原有平衡的旋转磁场被打破，BIM的气隙磁场在一个区域里得到增强，在其对称区域减弱，磁场增强的方向产生麦克斯韦力。如图2所示，电流I1和I2分别通入转矩控制绕组和悬浮控制绕组中，产生磁链ψ1和ψ2。

图2 产生可控径向悬浮力的原理图

在忽略负载的情况下，由于在气隙上方ψ1和ψ2方向相同，合成磁密增强；在气隙下方ψ1和ψ2方向相反，则合成磁密会减弱，从而磁拉力发生变化，会产生沿y轴正方向径向悬浮力Fy。若将反向电流通入到悬浮控制绕组中，就能产生沿y轴负方向的径向悬浮力。同理，若将与I2垂直的电流通入悬浮绕组中，则就能产生沿x轴方向的径向悬浮力Fx。

2 BIM数学公式模型

实际运行过程中，电动机存在复杂的电磁转矩和径向悬浮力之间耦合以及磁路饱和效应等问题，使得建立BIM模型的过程十分繁杂，因此需要做一些合理的假设以简化分析。假设如下：

(1) 整个磁路只计气隙磁阻，不考虑其他磁阻及损耗；

(2) 通入定转子绕组的电流是三相对称的；

(3) 忽略转子偏心不计；

(4) 忽略电动机的磁饱和，并认为径向力绕组的作用只起励磁，不对转矩磁链产生影响；

(5) 忽略电动机发热引起的温度变化等因素的影响。

2.1 径向悬浮力数学模型

根据悬浮原理可得，当转矩绕组极对数p1与悬浮绕组极对数p2满足p2=p1+1时，则产生的洛伦兹力(下文中其大小用F1表示)和麦克斯韦力(下文中其大小用Fm表示)方向相同，那么产生的合力F=Fm+Fl即为悬浮力的可控分量，且在d，q轴旋转磁场坐标系下的用磁链表示的悬浮力公式：

(1)

式中：ψd1，ψq1为气隙磁链分量；K=Km+Kl，Km为麦克斯韦常数，Kl为洛伦兹力常数；下标1，2分别表示BIM在转矩绕组侧和悬浮力绕组侧分量；下标s为对应定子分量。

由于重力的作用，转子将不可避免地发生偏心，造成气隙磁场失衡，在转子上会产生一种固有的麦克斯韦力，其表达式：

(2)

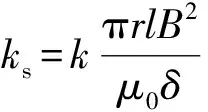
2.2BIM转矩绕相关数学方程

BIM中通入转矩控制绕组电流和通入悬浮力绕组电流产生的复合磁场在转子上感应得到感生电流，从而产生电磁转矩。依据上文合理假设，忽略悬浮力绕组的磁场在转子中产生的电流，由此得到BIM在d-q旋转坐标系中的定转子电压、磁链和转矩方程如下[4]：

1) 定子、转子电压方程：

(3)

式中：us1d，us1q表示定子d，q轴电压；is1d，is1q表示定子d，q轴电流；ψ1d，ψ1q表示定子d，q轴磁链；R1s， R1r表示定、转子电阻；ω1表示定子同步角速度；ωr表示转子角速度；p表示微分算子。

2) 转子磁链方程：

(4)

由式(4)解出：

(5)

将式(5)代入转矩方程，得出电磁转矩：

(6)

再将式(5)代入转子磁链微分方程并消去定子磁链分量，得到：

(7)

式中：Tr=Lr/Rr表示转子时间常数；ψr1d，ψr1q表示转子d，q轴磁链；Lr表示转子自感；p1表示转矩绕组极对数。

2.3BIM运行时状态方程

BIM运行时，其转子在径向悬浮力、电磁转矩和负载共同作用下的运动方程：

(8)

式中：x，y分别代表转子偏心位移在坐标轴x，y轴方向上的分量；m为转子质量；J为转动惯量；TL为负载转矩；p1为转矩绕组极对数。

3 BIM解耦控制策略国内外研究现状

目前，国内外已经对BIM开展了大量研究工作，国外主要有瑞士的R. Schoeb和日本的A. Chiba等，国内在国家自然科学基金项目、国家高新技术研究发展计划、省部级项目基金的资助和相关部门的大力支持下，各高校对无轴承电动机的研究取得了显著进展。

苏黎世联邦工学院于1996年研制出首台BIM，这一创新具有划时代的意义[3]，随后各国学者对BIM进行了广泛而深入的研究。文献[4]中瑞士学者为了实现BIM电磁转矩和径向力之间的解耦控制，提出一种近似线性化的控制算法，并且研制出功率为4 kW的四自由度样机本体和其相关控制系统对其进行控制。文献[5-7]中日本学者对BIM的基本特性进行了研究，并通过实验检测得到BIM定子中转矩绕组和悬浮力绕组之间的互感矩阵，以此建立径向悬浮力的解析公式。此外还对悬浮力和电磁转矩耦合的实质进行剖析，得出若要实现悬浮力和电磁转矩之间的解耦控制，必须对BIM定子绕组电流的幅值和相角进行补偿，使得旋转磁场保持平稳转动和幅值恒定，并基于此提出了一种气隙磁场定向控制方法，同时应用PID控制器及滞环控制策略实现了BIM空载运行时的悬浮控制。此外还研究了电动机的无传感器检测技术，并做了验证性实验。在国内，沈阳工业大学针对感应式、永磁式和磁阻式这三种不同转子结构的无轴承电动机，给出了通用的悬浮力解析方法，并利用ANSYS等软件验证了这些电动机的模型精度。此外还深入研究分析了无轴承电动机径悬浮力绕组励磁及其控制方式，得出定子绕组极对数的选取方案决定悬浮力绕组电能传递方向及其励磁方式的结论[8-9]。南京航天航空大学对BIM开展了磁场(气隙磁场和转子磁场)定向控制和悬浮子系统独立控制研究[10]，为BIM实用化提供新的思路。浙江大学的研究主要集中在综合考虑BIM工作时各种影响因素的精确解析模型和通过优化气隙磁场以实现电磁转矩和径向悬浮力之间解耦的控制策略[11-13]。江苏大学则着重在BIM参数优化设计[14-16]、精确数学模型建立、基于逆系统和神经网络逆系统、支持向量机逆系统理论的非线性解耦控制[17-20]、无传感运行以及高速数字实时控制系统实验[21]等方面的研究。

4 解耦控制相关技术及研究方向

本文详细介绍了目前BIM的解耦控制策略及其关键技术，并提出优化改进意见。

4.1 矢量控制技术

作为经典的电动机控制方法，矢量控制技术根据旋转坐标轴定向方法的不同可分为三种类型：①基于气隙磁场定向的BIM矢量控制方法；②基于转子磁场定向的BIM矢量控制方法；③BIM定子磁场定向控制方法。其中，第三种控制方法由于需要编写复杂的程序，花费时间很长，且不易于掌握和实现，因而无法在工业生产中推广，且在电动机低速运行时，不能对定子磁通进行准确测量，控制效果也不尽如人意。

由BIM的数学模型可知，径向悬浮力和电磁转矩是通过气隙磁链耦合产生的，因此首先考虑采用气隙磁场定向控制方法来解除耦合效应，图3为气隙磁场定向控制方法框图。上述控制方法将整个控

图3 基于气隙磁场定向的BIM矢量控制方法

制系统分为悬浮和旋转两部分分别控制，实现了悬浮力和电磁转矩的单独控制即可达到解耦效果[22]。但是由于该方法对转矩的控制效果还不稳定，没有实现真正的解耦，需要额外增加解耦器，就会增加系统的复杂性，降低可靠性，而且该方法对电动机参数的变化反应比较敏感，不利于实现无传感检测技术，因此潜在的研究和应用价值有限。为了进一步缓解耦合效应，优化控制性能，文献[4]提出了BIM转子磁场定向控制方法，控制框图如图4所示。该控制方法控制方式相对比较简单，所以应用广泛[4]。缺点是在应用过程中，控制精度受转子时间参数影响较大，系统的控制性能不佳，有待进一步优化改进。

图4 基于转子磁场定向的BIM矢量控制方法

4.2 直接转矩控制方法

文献[23]提出了基于空间矢量脉宽调制的BIM直接转矩控制方法，以解决传统直接转矩控制方法控制BIM时存在的转矩脉动和电流总谐波失真等问题。该方法核心思想：为了磁链滞环和转矩滞环的控制相互独立且互不干扰，引入了定子磁链同步角的修正环节；此外通过仿真实验，分析了PWM占空比与输出电压总谐波失真之间的关系，并基于此提出改进的优化占空比调制方法；通过该控制算法辨识得到的定子磁链值减去定子漏磁来获得悬浮力绕组控制所需要的气隙磁链，不须另外建立磁链观测器来估算磁链值或者在定子侧安装探测线圈以检测磁链信息，使得控制系统大大简化，同时提高系统稳定性。最后通过实验结果表明，采用该方法抑制了上文所述的问题，BIM的悬浮性能因此得到大幅提高。

然而传统电压模型法辨识气隙磁场的幅值和相位时，由于纯积分环节的直流增益为无穷大，辨识精度必然会影响。文献[24]提出了一种改进的电机磁链辨识算法，该方法的主体思想是用1个高通滤波器代替纯积分环节，为了解决高通滤波器带来的相位偏差，增加1个坐标变换环节，由此解决纯积分问题。实验结果表明采用该算法可以将纯积分环节存在的问题有效地消除，保证了在动静态过程中，电机磁链辩识精度都能保持在较高程度。通过应用用类似磁链辨识方法可以提高BIM磁链的辨识精度，则BIM的控制性能可以得到进一步提升。

4.3 独立控制方法

文献[25]提出了一种BIM独立控制策略，由于径向悬浮力的控制只与转矩绕组气隙磁链的幅值和相位相关，因此若能有效地探测或辨识该磁链的精确信息，便能够实现对悬浮子系统的独立控制，从而转矩子系统可以当作近似为传统异步电动机来控制，为BIM在高速、超高速领域实用化了打开了新的突破口。此外理论上可以选择任意控制方法来控制转矩绕组，特别是可以使用技术成熟且成本大幅降低的通用变频器来控制，BIM的实用性得到极大的提高。

由于悬浮子系统侧是采用经典PID控制器控制，该方法在参数匹配良好条件下能保证系统稳定，若系统参数发生变化或突加负载扰动，亦或模型误差和径向位移扰动都将导致控制性能变差。针对以上缺陷可以将以控制系统内部某些信号间传递函数的H∞范数为优化指标的H∞控制理论应用在控制器中，则系统的抗干扰能力和鲁棒稳定性能够得到较大程度提高[26]。

4.4 精确线性化方法

鉴于对线性系统的控制技术相对比较完善和成熟，如果将BIM这一复杂的难以控制的高阶非线性系统转换成易于实现最优控制效果的线性系统，就能采用现有的线性系统控制理论进行更好的控制。在这样的思想指导下，专家学者就提出了采用精确线性化控制方法将BIM的输入/输出变量和过程状态反馈线性化之后，再利用线性控制理论实现对线性系统的控制，从而将复杂问题简单化。系统线性化的实现可以通过很多种理论方法，目前最常用的是微分几何方法。文献[27]采用微分几何精确线性化方法来控制转子悬浮力子系统。该方法将原来非线性系统完全线性化成两个没有耦合关系的径向位置子系统，然后采用滑模变结构控制器分别控制这两个独立的位置子系统，从而构成整个系统的闭环控制。

4.5 逆系统及其与神经网络等相结合的方法

逆系统方法近年来被普遍的应用到对BIM控制当中，其本质上也属于一种非线性反馈线性化方法。与精确线性化方法相比，该方法不需使用抽象的数学理论，概念简明清晰、易于理解、使用方便[2,28]。对于BIM这个多输入多输出系统，该方法可以将各个原先具有耦合关系的变量解耦成可以单独控制且互不干扰的独立变量。但是，在实践过程中，逆系统方法的缺点也日益凸显，因为逆系统方法需要获取BIM的精确数学模型和其逆模型，这些都是很难精确描述的。

鉴于目前人工智能控制方法研究取得了突破性发展，神经网络与逆系统结合的方法被相关专家提了出来。该方法的基本指导思想是借助神经网络的辨识能力，来获取不确定非线性系统的逆模型，省去了计算逆系统解析表达式等一系列繁琐过程，克服了逆模型难以获取的困难，提高了逆系统的线性化能力，这解决了逆系统应用上的一大难题，具有很大的优越性[29-30]。当然，逆模型的获取还有其他很多办法，通过查阅国内外相关文献可知，支持向量机又是目前控制领域的一大研究热点[31]。不管是利用神经网络还是支持向量机与逆系统方法相结合，其网络结构形式与传统的逆系统结构没有两样，基本指导思想都是一致的，但是任何控制方法都有利弊两个方面，学习速度慢、训练时间长、理想样本难以获取等都是需要我们进一步解决的问题。

4.6 无速度和无位置传感器技术

在BIM控制系统中，转速信息通常采用光电编码盘来检测获得，位置信息则由电涡流传感器检测得到。然而传感器本身在构造上高速、超高速化难以或无法实现，所以在电机低速运行时，检测的信息满足误差精度要求，而在电机运行于高速、超高速情况时测量精度就达不到或者而产生错误信号，导致故障甚至事故。而且使用传感器不仅增加了控制系统成本，而且存在安装与维护上的困难，使系统易受干扰，降低了系统可靠性，限制了BIM的应用领域[21]。针对这一系列问题，无传感技术应运而生。随着研究的深入，基于人工神经元网络法、模型参考自适应方法、动态转速估计器法、自适应转速观测器法、基于PI自适应控制器法、凸极跟踪法、转子齿谐波法等已广泛应用于无转速传感器技术中，相关技术已经应用到BIM无速度传感器控制中。而在转子位移控制系统中，也可以采用无传感技术获得转子的径向偏心位移[32]。

BIM无传感技术的研究起步较晚，且实用化产品并未广泛使用，具有极高的研究价值。

5 结 语

随着我国经济发展和科技进步，BIM由于其体积小、能量消耗小、较短的轴长和更高的临界速度等优点在很多特殊的电气传动领域有着广泛应用前景。本文在研读相关学术论文以及深入研究BIM工作原理及数学模型基础上，分析解耦控制关键技术研究现状及其优缺点，并针对性探讨了一些改进方法和发展方向。

[1] SALAZAR A O,CHIBA A,FUKAO T.A review of developments in bearingless motors[C]//7th international symposium on magnetic bearings,Zurich.2000:335-400.

[2] ZHU H Q,ZHOU Y,LI T B,et al.Decoupling control of 5 degrees of freedom bearingless induction motors using α-th order inverse system method[J].Acta Automatica Sinica,2007,33(3):273-278.

[3] SCHÖB R.Beiträge zur lagerlosen asynchronmaschine[D].Zürich,Switzerland:Eidgenoessische Technische Hochschule(ETH),1993.

[4] SCHÖB R, J. BICHSEL J.Vector control of bearingless motor[C]//4th International Symposium on Magnetic Bearings,Zürich,Switzerland.1994:327-332.

[5] SUZUKI T,CHIBA A,RAHMAN A,et al.An air-gap-flux-oriented vector controller for stable operation of bearingless induction motors[J].IEEE Trans.on Industry Applications,2000,36(4):1067-1076.

[6] FUJISHIRO T,HANAWA R,SAKATA Y,et al.An analysis of an induction bearingless motor with a squirrel cage totor[C]//8th International Symposium on Magnetic Bearings,Mito,Japan.2002:253-258.

[7] TERA T,YAMAUCHI Y,CHIBA A,et al.Performances of bearingless and sensorless induction motor drive based on mutual inductions and rotor displacements estimation[J].IEEE Transactions on industrial Electronics,2006,53(l):187-194.

[8] WANG B G,WANG Z,WANG F X.Levitation force control by current vector orientation for a bearingless motor with hybrid rotor structure[C]//IEEE Electrical and Computer Engineering,Canadian.IEEE,2003:383-386.

[9] 王凤翔,王宝国,徐隆亚.一种新型混合转子结构无轴承电动机磁悬浮力的矢量控制[J].中国电机工程学报,2005,25(5):98-103.

[10] 邓智泉,张宏全,王晓琳,等.基于气隙磁场定向的无轴承异步电机非线性解耦控制[J].电工技术学报,2002,17(6):19-24.

[11] 年珩,贺益康.感应型无轴承电机磁悬浮力解析模型及其反馈控制[J].中国电机工程学报,2003,23(11):139-144.

[12] HE Y K,NIAN H.Analytical model and feedback control of the levitation force for an induction-type bearingless motor power electronics and drive systems[C]//5th International Conference on Power Electronics and Drive Systems,Singapore.2003:242-246.

[13] 贺益康,年珩,阮秉涛.感应型无轴承电机的优化气隙磁场定向控制[J].中国电机工程学报,2004,24(6):116-121.

[14] 张涛,朱愰秋,孙晓东,等.基于有限元法的高速永磁转子强度分析[J].电机与控制学报,2012,16(6):63-68.

[15] 项倩雯,孙玉坤,张新华.磁悬浮开关磁阻电机建模与参数优化设计[J].电机与控制学报,2011,15(4):74-79.

[16] 朱熀秋,陈雷刚,李亚伟,等.Halbach阵列无轴承永磁电机有限元分析[J].电机与控制学报,2013,17(4):39-44.

[17] 孙玉坤,任元,黄永红.磁悬浮开关磁阻电机悬浮力与旋转力的神经网络逆解耦控制[J].中国电机工程学报,2008,28(9):81-85.

[18] 朱志莹,孙玉坤,黄永红.磁悬浮开关磁阻电机逆动力学建模与控制[J].电机与控制学报,2011,15(3):79-85.

[19] SUN X D,ZHU H Q.Decoupling control of bearingless permanent magnet-type synchronous motor using artificial neural networks-based inverse system method[J].International Journal of Modelling Identification and Control,2009,8(2):114-121.

[20] SUN X D,ZHU H Q.Artificial neural networks inverse control of 5 degrees of freedom bearingless induction motor[J].International Journal of Modelling Identification and Control,2012,15(3):156-163.

[21] 孙晓东,朱愰秋,杨泽斌.基于左逆系统的无轴承异步电机无速度传感器运行[J].控制与决策,2012,27(8):1256-1260.

[22] 邓智泉,张宏荃,王晓琳,等.基于气隙磁场定向的无轴承异步电机非线性解耦控制[J].电工技术学报,2002,17(6):19-24.

[23] 王宇,邓智泉,王晓琳.无轴承异步电机的直接转矩控制技术研究[J].中国电机工程学报,2008,28(21):80-84.

[24] 王宇,邓智泉,王晓琳.一种新颖的电机磁链辨识算法[J].中国电机工程学报,2007,27(6):39-44.

[25] 邓智泉,王晓琳,李冰,等.无轴承异步电机悬浮子系统独立控制的研究[J].中国电机工程学报,2003,23(9):107-111.

[26] 黄雷,赵光宙,年珩,贺益康.永磁型无轴承电机悬浮系统的H∞鲁棒控制[J].控制理论与应用,2008,25(4):711-716.

[27] 董磊,刘贤兴,孙宇新.无轴承异步电机径向悬浮力的微分几何变结构解耦控制[C]//第26届中国控制会议.2007:17-21.

[28] 孙玉坤,费德成,朱熀秋.基于α阶逆系统五自由度无轴承永磁电机解耦控制[J].中国电机工程学报,2006,26(1):120-126.

[29] 孙晓东,朱熀秋.基于神经网络理论无轴承异步电动机解耦控制[J].电工技术学报,2010,25(1):43-49.

[30] SUN X D,CHEN L,YANG Z B,et al.Speed-sensorless vector control of a bearingless induction motor with artificial neural network inverse speed observer[J].IEEE/ASME Transactions on Mechatronics,2013,18(4):1357-1366.

[31] 黄正奇,黄学良.基于支持向量机逆系统的无轴承异步电机非线性解耦控制[J].电工技术学报,2015,30(10):164-170.

[32] 年珩,贺益康.永磁型无轴承电机无径向位移传感器运行研究[J].电工电能新技术,2006,25(4):15-25.

The Research Status of Decoupling Control for Bearingless Induction Motors

SUNYu-xin,QIANZhong-bo

(Jiangsu University, Zhenjiang 212013, China)

Due to no friction between the bearing and the rotor, the bearingless induction motor is not required to add the lubricating oil in high speed operation, and it also has the characteristics of low noise and low vibration. So bearingless induction motor is very important in the field of electrical transmission. While there is a very complex electromagnetic relationship in the bearingless induction motor, so the decoupling control must be carried out. In this paper, the working principle and the mathematical model of the bearingless induction motor were described,and the research results of the decoupling control strategy for the bearingless induction motor were summarized. The advantages and disadvantages of the decoupling control strategy were also analyzed and compared. Finally, the future research and development direction of decoupling control was put forward.

bearingless induction motor (BIM); working principle; mathematical model; decoupling control method; research development direction

2015-11-27

国家自然科学基金项目(61174005)

TM343

A

1004-7018(2016)05-0077-06

孙宇新(1968-)，女，博士研究生，副教授，研究方向为无轴承电机控制、神经网络及非线性控制等。