趋近律参数优化的永磁同步电动机模糊滑模控制

姚江云，吴方圆 ，覃 溪

(1.广西科技大学 鹿山学院，柳州 545616；2广西科学技术情报研究所,南宁 530022)

趋近律参数优化的永磁同步电动机模糊滑模控制

姚江云1，吴方圆2，覃 溪1

(1.广西科技大学 鹿山学院，柳州 545616；2广西科学技术情报研究所,南宁 530022)

研究了一种趋近律参数优化的模糊滑模控制方法，应用到永磁同步电动机转速控制中。采用神经网络优化趋近律参数，提取趋近律参数的最优曲线，在此基础上设计了滑模变结构控制器实时修正趋近律参数，最后应用到PMSM转速控制中。仿真及实验结果表明，该方法具有良好的静态、动态特性和鲁棒性。

永磁同步电动机；趋近律参数优化；滑模控制；转速控制

0 引 言

永磁同步电动机(以下简称PMSM)是一个非线性强耦合的系统，若采用常规的PID 控制，很难得到满意的控制效果。文献[1-2]采用了传统滑模控制进行了转速环的设计，文献[3]设计了一种基于新型趋近率的PMSM滑模控制策略，都取得较为良好的效果。但都没有对趋近律的不确定参数进行处理，都是取最大值最小值或粗劣估算，使得控制器参数不能针对控制对象模型的变化而变化。

本文设计了一种趋近律参数优化的滑模变结构控制方法。具体方案为首先搭建传统的PMSM滑模控制模型，使其在全速、重载、空载、干扰等各种工况下运行，然后提取数据并导入设计好的RBF神经网络模型中进行训练，提取趋近律参数最合适的变化范围，用来设计滑模滑模变结构控制器，最后将此方法应用到PMSM的调速控制中，有利于控制性能的进一步提高。

1 PMSM建模

建立永磁同步电动机d,q轴转速数学模型，当id=0时，如下式：

(1)

d，q轴电流数学模型如下：

(2)

式中：Ld,Lq为d，q轴定子电感;p为极对数；id,iq为d，q轴定子电流;ud,uq为d,q轴定子电压;R为定子绕组;ψf为转子磁通;ωr为转子角速度;B为阻力摩擦系数;J为转动惯量。

2 整体控制方案设计

能够使滑模控制器以何种规律趋近并沿滑模面不断变化的重要因素就是趋近律，一般在滑模变结构控制中都使用指数趋近律设计滑模控制器，即:

(3)

式中：ε,k为不确定参数，k具有改进系统的动态特性的作用，能够改变系统向滑模面的趋近速率，ε具有消除摄动及外干扰的作用。根据文献[4-5]所设计的滑模控制器模型可知，在实际应用时，对于趋近律中的ε,k均作保守估计，取一个很大的值或取一个很小的值，这样会使系统穿越滑模面时速度很大而导致抖动增强，或者速度很慢导致系统实时性差。因此，本文决定首先根据实际控制对象，寻找ε,k的最佳取值范围，然后以此范围为限制，设计滑模控制器，最后通过不断采集PMSM的相关参数，通过模糊控制计算出最合适的ε,k参数值，对ε,k在规定的范围内进行实时修改，使得整个滑模控制器以最快的速度平稳准确地到达滑模面，相比于直接取最大值的方法能够减小抖动，改善控制性能。图1为整体结构框图。

图1 整体控制结构框图

3 趋近律参数的优化

设计中采用RBF神经网络作为参数优化器[6-7]。首先在Simulink中搭建基于传统滑模变结构控制的PMSM控制模型，然后分别在全速范围内重载、空载、扰动情况下运行，并采集此时的d，q轴的电流id,iq，电机的转速ω作为RBF神经网络的输入量，在滑模控制器趋近律不确定参数ε,k的最大取值范围内将其离散化，将离散化后的数据作为RBF神经网输出量对其进行训练，最后选取ε,k输出数据最为集中且平滑的曲线作为最终的ε,k参数变化范围，此时ε,k的取值范围远远小于原始的取值范围，进而能够保证控制精度及系统的平稳性。RBF神经网络的结构采用3-5-2结构，图2为本文经过多次训练后，得到的ε,k的最优取值范围曲线。

图2 趋近律参数优化取值范围

在传统的滑模控制中，一般k为(0，10)，ε为(0，20)。由图可知，在全工况情况下，经过优化后k的取值范围为(3，8.5)，ε的取值范围为(7，17)，相比于传统的经验法取值法，取值范围减小了，这样可以避免在控制过程中出现的剧烈抖动，进而提高系统的控制精度和稳定性。

4 趋近律参数优化后的PMSM模糊滑模转速控制

4.1 转速滑模控制器的设计

(1)滑模面的设计

状态变量:

(4)

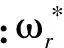
(5)

滑模面选用积分滑模面如下:

(6)

代入状态变量得:

(7)

(2)速度控制量的输出

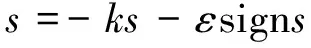
(8)

式中:ε=(7，17),k=(3，8.5)。

对滑模面求导得:

(9)

联立状态方程和滑模面可得:

(10)

4.2 基于模糊控制的参数修正

为了使趋近律参数的每一次取值都尽量接近控制目标，本文通过不断采集系统运行过程中的相关参数，采用模糊控制设计了趋近律参数修正控制器。由式(10)可知，ε,k的取值与iq，转速ω具有一定的解析关系，因此可以根据此关系设计控制ε,k变化的模糊控制器来根据系统运行情况不断修正参数。分别将iq，ω,ε,k的具体取值范围转换到规范论域，并对应到设置的语言变量，iq，ω为[SMB]，ε,k为[VSSMBVB]中，选取高斯隶属函数，模糊控制规则一般是根据经验及推理后设定的，规则如表1所示。

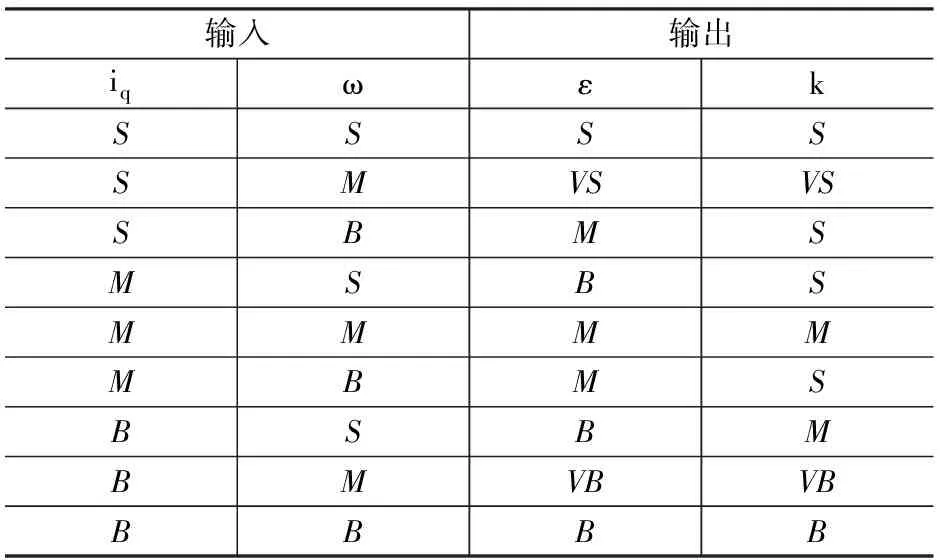
表1 模糊规则推理表

5 控制系统的仿真及实验验证

为了初步验证本算法的有效性，只在速度环上应用本算法，而电流环仍然采用传统PI控制。首先在Simulink环境下建立仿真模型进行仿真，然后以DSPTMS320F2812为主控制器，搭建硬件平台，进行控制算法的实验验证。控制系统整体建立步骤流程如图3所示。

图3 控制系统工作流程

仿真及实验系统中选取的电机参数：额定功率PN=1kW，额定转速ωr=2 500r/min,定子电阻R=0.95Ω，永磁体磁链ψf=0.245 2Wb，定子d，q轴电感Ld=3.5mH，Lq=15mH,定子转动惯量J=0.002kg·m2，电机极对数p=4。图4为搭建的硬件实验系统。

图4 硬件实验系统

图5为传统滑模变结构控制与趋近律参数优化后的模糊滑模变结构控制下PMSM转速响应曲线。由图5(a)可知，传统的滑模变结构控制超调量大，且系统的跟踪性能较差，系统在0.2s时加入随机扰动之后抖动较大。图5(b)、图5(c)为改进后的控制算法的仿真及实验结果，可见改进后的方法进一步减少了系统超调量，且提高了控制精度，系统在加入随机扰动之后，系统抖动较小，恢复稳定速度较快。

(a)传统滑模控制转速跟踪(b)趋近律参数优化后的模糊滑模控制仿真

(c) 趋近律参数优化后的模糊滑模控制实验

图5 转速跟踪曲线

图6(a)为传统滑模控制器的输出。由于滑模控制器不能够对外在模型参数变化进行实时预测，使得控制器的输出抖动较大。图6(b)、图6(c)分别为改进后的控制器输出的仿真及实验结果。由于趋近律参数取值范围集中，且在运行过程中模糊滑模控制器能够对其进行实时修正，使得控制器的输出抖动较小。

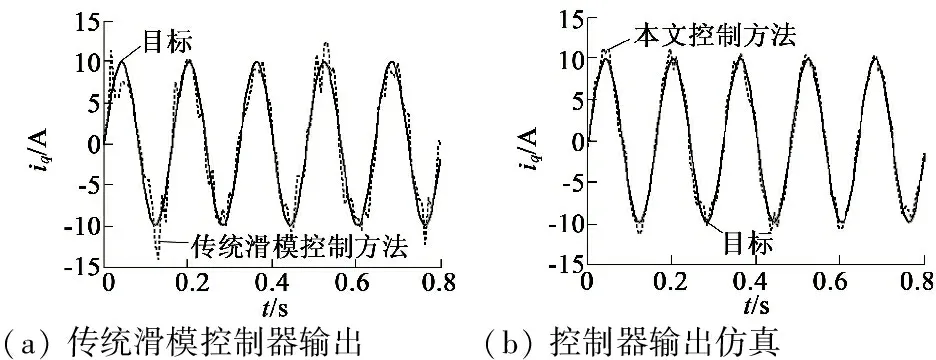
(a)传统滑模控制器输出(b)控制器输出仿真

(c) 控制器输出实验

图6 控制器输出曲线

图7是给定负载下的转速响应曲线。在一定负载转矩下给定转速800 r/min,在0.15s时负载转矩增加，比较转速的变化情况；在0.35 s时给定转速变为1 400 r/min，比较转速的响应情况。图7(a)为传统滑模控制下的转速响应曲线，系统起动时抖动较大，在一定转速下，增加负载也会引起系统抖动，且在给定转速上升时，系统跟踪过程中超调较大。图7(b)、图7(c)为改进后的控制算法的转速响应曲线，系统起动时抖动较小，在一定转速下，适当增加负载，系统能够快速恢复平稳，且在给定转速上升时，系统跟踪过程中超调较小。

(a)传统滑模控制(b)趋近律参数优化后的模糊滑模控制仿真

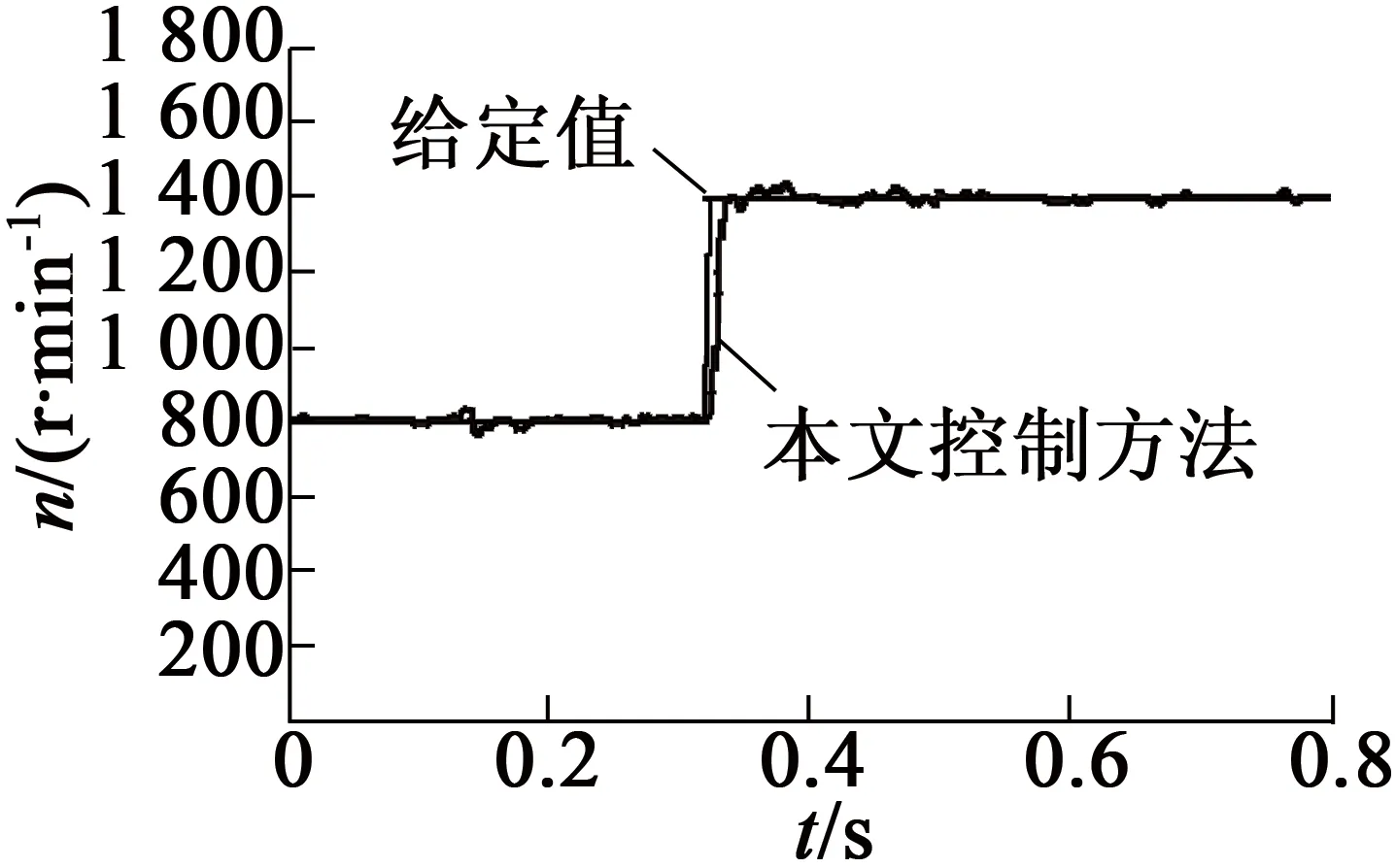
(c) 趋近律参数优化后的模糊滑模控制实验

图7 定负载下的转速响应曲线

6 结 语

本文设计了一种趋近律参数优化的模糊滑模控制方法，并将其应用到PMSM控制中取得良好的控制效果。本设计的不足之处是所研究的控制算法只在PMSM的转速控制中较为有效，而对于位置控制是否同样有效，还需要进一步的实验研究。

[1] 贺宇轩，解小华，张爱春.基于滑模变结构控制的永磁同步电机[J].吉林大学学报(信息科学版)，2015，33(1)：12-17.

[2] 张涌松，舒志兵.基于永磁同步电机的滑模变结构仿真研究[J].机床与液压，2008，36(7)：288-292．

[3] 童克文，张兴，张昱，等.基于新型趋近律的永磁同步电机滑模变结构控制[J].中国电机工程学报，2008，28(21):102-106.

[4] 王志宇，王长松，范普成，等.基于滑模变结构的永磁同步电机调速系统设计[J].微电机，2011,44(6)：52-56.

[5] 茅靖峰，吴爱华，吴国庆，等.永磁同步电机幂次变速趋近律积分滑模控制[J].电气传动，2014，44(6)：50-53.

[6] 尹西杰，徐建国.无刷直流电机的神经滑模变结构控[J].计算机仿真，2014，31(8)：402-406．

[7] 李文波，王耀南.基于神经网络补偿的机器人滑模变结构控制[J].计算机工程与应用,2014,50(23):251-255.

Research on Fuzzy Sliding Mode Control of PMSM Based on Reaching Law Parameters Optimization

YAOJiang-yun1,WUFang-yuan2,QINXi1

(1.Lushan College of Guangxi University of Science and Technology，Liuzhou 545616,China;2.Institute of Science and Technology Information of Guangxi,Nanning 530022,China)

The fuzzy sliding mode variable structure control method based on reaching law parameters optimization was researched and applied to the speed control drive system in double closed loop of PMSM. First, the reaching law parameters was optimized by neural network, and extract the optimal parameters curve was extracted of reaching law.A fuzzy sliding mode controller based on the reaching law parameters optimization was designed, and applied to PMSM speed control system. The simulation results show that speed control system has good static, dynamic characteristics and anti-interference ability.

PMSM; reaching law parameters optimization; sliding mode control; speed control

2015-10-20

广西科技大学鹿山学院自然科学基金项目(2013-LSZK08)

TM341;TM351

A

1004-7018(2016)05-0056-04

姚江云(1987-)，女，硕士，讲师，研究方向为电气自动控制系统研究与设计。