基于线性状态反馈的直流微电网稳定方法

杨忠林 ，查晓明 ，孙建军 ，刘 飞

（1.武汉大学 电气工程学院，湖北 武汉 430072；2.海军工程大学 电气工程学院，湖北 武汉 430033）

0 引言

近年来，在能源需求和环境保护的双重压力下，将分布式电源、储能装置、可控负载结合在一起的微电网获得了越来越多的重视和应用［1-3］。相对于交流微电网，直流微电网具有效率高、控制简单、可靠性高及电能品质好等优点，正逐步受到日益广泛关注［4-7］。然而，直流微电网中含有大量的电力电子装置，其特性相对于微电网表现为恒功率负载，可能引起直流微电网母线电压的不稳定［8-11］。

文献［12-13］对直流电网的稳定性问题进行了分析并提出了相应的稳定性准则，这些稳定性准则提出了直流电网稳定的充分条件和稳定裕度，但没有提出改善直流电网稳定范围的措施。文献［14-15］提出了修改系统电路结构或参数，增大系统的阻尼，从而提高直流微电网稳定性的方法，但这些方法会增加系统的体积和功耗。文献［16］通过增加有源阻尼信号改变大电网接口变换器的等效阻抗，进而提高直流微电网稳定性，然而该方法仅适用于微电网并网运行的工况。文献［11］提出在负荷点变换器中引入虚拟电容进而提高系统稳定性的方法，但该方法仅适用于单电源单负载的情况。文献［17］提出了通过改进的PID控制提高直流微电网电压稳定性的方法，但该方法仅适用于使用Buck变换维持直流母线电压的情况，并且控制器参数较多，在实际应用中难以确定合适的参数。本文通过引入线性状态反馈支路，抵消了恒功率负载对微电网稳定性的不良影响，提高了直流微电网的稳定性。该方法不仅适用于Buck变换器维持直流微电网母线电压的情况，而且适用于Boost变换器维持直流微电网母线电压的情况。

1 系统模型及其稳定性分析

典型的直流微电网结构如图1所示，其中包含大量的电力电子变换器。源侧AC/DC或DC/DC变换器连接于直流微电网，维持微电网母线电压。当负荷点变换器工作于恒压模式且控制性能良好时，负荷点变换器及其负载相对于直流微电网为恒功率负载［18］。而在通常气候条件下，为充分利用可再生能源，光伏和风电等分布式电源一般工作于最大功率点跟踪（MPPT）模式，此时的光伏和风电及其变换器可以看作是恒功率电源［19］。储能单元在其变换器的作用下，进行恒功率或恒流充放电，这时它们可以看作是恒功率源或恒流源。

图1 直流微电网结构Fig.1 Structure of DC microgrid

为分析简便，以最常用的分布式电源经过Buck和Boost变换器接入直流母线维持微电网母线电压为例，来研究系统的稳定性。

1.1 Buck变换器维持微电网母线电压的情形

图2 Buck变换器维持母线电压时直流微电网的简化模型Fig.2 Simplified model of DC microgrid when Buck converter maintains bus voltage

分布式电源经过Buck变换器接入直流母线维持微电网母线电压时，直流微电网的简化模型如图2所示。其中，E为Buck变换器的输入电压；L为Buck变换器的滤波电感；C为所有变换器电容并联后的等效电容；R为直接连接于直流母线的等效负载电阻；PCPL为等效的恒功率负载，其数值为恒功率负载的输入功率之和减去恒功率源的输出功率之和；ISE为恒流充放电控制的储能单元等效的恒流源。

根据电路结构，运用状态平均法列写电路方程，可得：

其中，d为Buck变换器的占空比，在开环控制中d为常数。对式（1）在其平衡点处进行小信号线性化，为使得系统的特征值实部小于零，可推导得出系统稳定的条件为［20］：

其中，UC为电容电压在平衡点处的稳态值。

1.2 Boost变换器维持微电网母线电压的情形

分布式电源经过Boost变换器接入直流母线维持微电网母线电压时，直流微电网的简化模型如图3所示。

图3 Boost变换器维持母线电压时直流微电网的简化模型Fig.3 Simplified model of DC microgrid when Boost converter maintains bus voltage

由图3列写电路方程，可得：

对式（3）在其平衡点处进行小信号线性化，可得系统稳定的条件为［20］：

由式（2）和式（4）可知，要使得直流微电网稳定，系统中的恒功率负载功率必须小于直接连接于直流母线的负载功率，即阻性负载的功率。而一个典型的直流微电网约含有80%～85%的恒功率负荷、15%～20%的阻性负荷［16］，因此系统难以稳定，需要采取措施，提高系统的稳定性。

2 基于线性状态反馈的直流微电网稳定方法

下面以Buck变换器为例，说明基于线性状态反馈的直流微电网稳定方法。根据式（1）可画出系统模型方框图如图4所示。图中VC在开环控制中为调制指令信号，在闭环控制中为闭环PI控制器的输出信号。VTr为三角载波信号的幅值，以下为分析方便，设VTr=1，即d=VC。从图中可以看出，恒功率负载的影响是方框图右下角中间的一条反馈支路，它给微电网带来了负增量阻抗，从而导致直流微电网不稳定。

图4 图2所示直流微电网的方框图Fig.4 Block diagram of DC microgrid shown in fig.2

为抵消恒功率负载的影响，在系统中引入一条线性反馈支路，如图5中左下角所示，线性反馈支路包括数乘器和微分器各一个。显然，反馈支路的引入并不改变系统的稳态平衡点（UC，IL）。通过合理选择反馈系数k，就可以抵消恒功率负载负增量阻抗的影响，提高系统的稳定性。

图5 带有线性反馈支路的直流微电网方框图Fig.5 Block diagram of DC microgrid with linear feedback branch

由图5可得：

由上式整理可得系统的状态方程为：

在平衡点处对式（6）进行小信号线性化，并整理为矩阵形式可得：

由式（7）整理可得系统的特征方程为：

由罗斯-霍尔维兹稳定性判据可知，系统稳定的充要条件为：

由式（9）可知，通过引入线性反馈支路，当反馈系数足够大时，反馈支路可以抵消恒功率负载负增量阻抗特性，增大了系统的阻尼，从而确保系统稳定。

3 低通滤波器在反馈支路中的应用

非线性反馈支路中的微分器虽然可以提高系统的稳定性，但会放大噪声，而电力电子变换器中会产生很多高次谐波，所以很少直接采用微分环节，可在微分环节前加入低通滤波器，如图6所示。

图6 加入低通滤波器和线性状态反馈的直流微电网方框图Fig.6 Block diagram of DC microgrid with low-pass filter and linear state feedback

图中ωr为低通滤波器的截止角频率，显然其数值应小于Buck变换器的开关频率。为了分析k和ωr的取值范围，确保系统稳定，下面列写出系统的状态方程并进行小信号稳定性分析。

令：

由图6可得：

整理可得系统的状态方程为：

在平衡点处对式（12）进行小信号线性化，并整理为矩阵形式可得：

由式（13）整理可得系统的特征方程为：

由罗斯-霍尔维兹稳定性判据可得系统稳定的充要条件为：

经整理可知，为了使得微电网稳定，反馈系数k和截止角频率ωr需满足以下条件：

4 线性状态反馈在Boost变换器中的应用

如图7所示，为抵消恒功率负载的影响，在系统中引入一条含有低通滤波器的线性反馈支路。

图7 线性状态反馈在Boost变换器中的应用Fig.7 Application of linear state feedback in Boost converter

令：

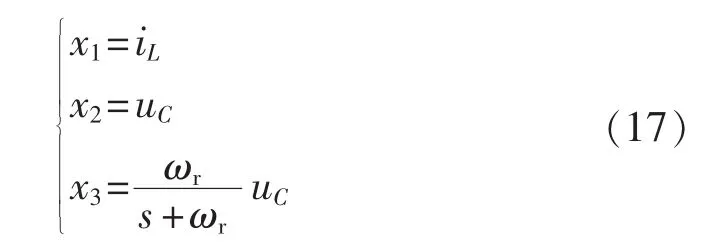
由图7可得：

整理可得系统的状态方程为：

由式（19）可知系统稳态时的电感电流可由下式求得：

在平衡点处对式（19）进行小信号线性化，并整理为矩阵形式可得：

将式（20）代入式（21），整理可得系统的特征方程为：

对比式（14）和式（22）可以看出，对于 Boost变换器的特征方程，其二阶项的系数中k前的符号出现了负号项，这就意味着k的取值并不是越大越好。假设系统的参数如下：E=150 V，VC=0.25，L=8 mH，C=0.5 mF，UC=200 V，R=40 Ω，PCPL=2 000 W，ωr=4 200 rad/s。k变化时系统极点的移动如图8所示。当k的取值较小时，随着k的增大，系统的特征根向s右半平面移动，这有助于增加系统的稳定性。但随着k的进一步增大，最终系统的特征根又开始向s左半平面移动，这可能导致系统不稳定。

图8 采用线性状态反馈的Boost变换器极点分布图Fig.8 Pole migration plot of Boost converter with linear state feedback

5 仿真实验

为了验证前面提出方法的有效性，本文分别针对Buck和Boost变换器维持微电网母线电压的情形，采用MATLAB/Simulink搭建了直流微电网的仿真实验模型，其系统结构如图9所示。

图9 实验系统Fig.9 Experiment system

5.1 Buck变换器维持直流母线电压的仿真

源侧变换器1为图6所示线性状态反馈控制的Buck 变换器，E=400 V，VC=0.5，L=8 mH，C=0.5 mF，UC=200 V。源侧变换器2为恒功率控制的变换器，其输出功率为500 W。恒功率负载的功率为2500 W，系统等效的恒功率负载为PCPL=2000 W。阻性负载的电阻值R=40 Ω。储能单元采用恒流充放电控制，其放电电流为3 A。变换器的开关频率为10 kHz。仿真实验结果如图10和图11所示。

当系统没有加入反馈控制支路时，对式（1）进行线性化，可计算得出系统的特征值为25±j499.375，直流微电网母线电压uC与Buck变换器电感电流iL的波形如图10所示，由于特征值的实部大于零，直流母线电压和电感电流发散，直到电感电流下降到零，直流母线电压维持大幅度振荡。

图10 Buck变换器维持直流母线电压，没有线性反馈控制时的母线电压和电感电流Fig.10 Bus voltage and inductance current，without linear feedback when Buck converter maintains DC bus voltage

图11 Buck变换器维持直流母线电压，引入反馈控制时的母线电压和电感电流Fig.11 Bus voltage and inductance current，with linear feedback when Buck converter maintains DC bus voltage

当系统加入线性反馈支路和低通滤波器时，由式（16）可得系数 ωr的取值范围为：ωr＞50 rad /s。 可取 ωr=1200 rad /s，k=1.5×10-5。 由式（14）可得系统在平衡点的特征值分别为-492.953±j1 259.054、-164.094。由于特征值的实部都小于零，系统稳定。直流微电网母线电压uC与Buck变换器电感电流iL的波形如图11所示。

5.2 Boost变换器维持直流母线电压的仿真

源侧变换器1为图7所示线性状态反馈控制的Boost变换器，E=150 V，VC=0.25，L=8 mH，C=0.5 mF，UC=200 V。系统中的其他设备参数同上节。仿真实验结果如图12和图13所示。

当系统没有加入反馈控制支路时，对式（3）进行线性化，可计算得出系统的特征值为25±j374.166，直流微电网母线电压uC与Boost变换器电感电流iL的波形如图12所示，由于特征值的实部大于零，直流母线电压和电感电流发散，直到电感电流下降到零，直流母线电压维持大幅度振荡。

图12 Boost变换器维持直流母线电压，没有反馈控制时的母线电压和电感电流Fig.12 Bus voltage and inductance current，without linear feedback when Boost converter maintains DC bus voltage

图13 Boost变换器维持直流母线电压，引入反馈控制时的母线电压和电感电流Fig.13 Bus voltage and inductance current，with linear feedback when Boost converter maintains DC bus voltage

当系统加入线性反馈支路和低通滤波器时，取ωr=6800 rad /s，k=1.3×10-5，由式（22）可以得到系统在平衡点的特征值分别为-738.117±j73.882、-1 737.766。由于特征值的实部都小于零，系统稳定。直流微电网母线电压uC与Boost变换器电感电流iL的波形如图13所示。

由以上实验可知：无论是Buck变换器，还是Boost变换器，通过引入线性状态反馈支路，都可以抵消恒功率负载的负阻抗特性，从而实现了直流微电网母线电压的稳定运行。

6 结论

针对直流微电网中恒功率负载可能会引起直流微电网母线电压不稳定的问题，本文通过引入线性状态反馈支路，抵消了恒功率负载的不良影响，从而确保了系统的稳定运行。该方法实现简单，适用范围广，不仅适用于Buck变换器，而且适用于Boost变换器。仿真实验结果验证了该方法的有效性。

［1］LU Xiaonan，GUERRERO J M，SUN Kai，et al.An improved droop control method for DC microgrids based on low bandwidth communication with DC bus voltage restoration and enhanced current sharing accuracy［J］.IEEE Transactions on Power Electronics，2014，29（4）：1800-1812.

［2］DRAGICEVIC T，GUERRERO JM，VASQUEZ JC，etal.Supervisory control of an adaptive-droop regulated DC microgrid with battery management capability［J］.IEEE Transactions on Power Electronics，2014，29（2）：695-706.

［3］TANG Xisheng，DENG Wei，QIZhiping.Investigation ofthe dynamic stability of microgrid［J］.IEEE Transactions on Power Systems，2014，29（2）：698-706.

［4］LU Xiaonan，SUN Kai，GUERRERO J M，et al.State-of-charge balance using adaptive droop controlfordistributed energy storage systems in DC microgrid applications［J］.IEEE Transactions on Industrial Electronics，2014，61（6）：2804-2815.

［5］ANAND S，FERNANDES B G.Reduced-order model and stability analysis of low-voltage DC microgrid［J］.IEEE Transactions on Industrial Electronics，2013，60（11）：5040-5049.

［6］郝雨辰，吴在军，窦晓波，等.多代理系统在直流微网稳定控制中的应用［J］.中国电机工程学报，2012，32（9）：27-34.HAO Yuchen，WU Zaijun，DOU Xiaobo，etal.Application of multi-agent systems to the DC microgrid stability control［J］.Proceedings of the CSEE，2012，32（9）：27-34.

［7］吴卫民，何运彬，耿攀，等.直流微网研究中的关键技术［J］.电工技术学报，2012，27（1）：98-105.WU Weimin，HE Yunbin，GENG Pan，et al.Key technologies for DC micro-grids［J］.Transactions of China Electrotechnical Society，2012，27（1）：98-105.

［8］DU Weijing，ZHANG Junming，ZHANG Yang.Stability criterion for cascaded system with constant power load［J］.IEEE Transactions on Power Electronics，2013，28（4）：1843-1851.

［9］MARX D，MAGNEP，NAHID-MOBARAKEH B.Largesignal stability analysis tools in DC power systems with constant power loads and variable power loads-a review［J］.IEEE Transactions on Power Electronics，2012，27（4）：1773-1787.

［10］ASHOURLOO M，KHORSANDI A，MOKHTARI H.Stabilization ofDC microgridswith constant-powerloadsby an active damping method ［C］∥4th Power Electronics，Drive Systems&Technologies Conference.Tehran，Iran：［s.n.］，2013：471-475.

［11］MAGNEP，MARX D，NAHID-MOBARAKEH B.Large-signal stabilization of a DC-link supplying a constant power load using a virtual capacitor：impact on the domain of attraction［J］.IEEE Transactions on Industry Applications，2012，48（3）：878-887.

［12］WILDRICK C M，LEE F C，CHO B H，et al.A method of defining the load impedance specification for a stable distributed power system［J］.IEEE Transactionson PowerElectronics，1995，10（3）：280-285.

［13］FENG Xiaogang，LIU Jinjun，LEE F C. Impedance specificationsforstable DC distributed powersystems ［J］.IEEE Transactions on Power Electronics，2002，17（2）：157-162.

［14］KWASINSKI A，ONWUCHEKWA C N.Dynamic behavior and stabilization ofDC microgrids with instantaneous constantpower loads ［J］.IEEE Transactionson PowerElectronics，2011，26（3）：822-833.

［15］CESPEDES M，XING Lei，SUN Jian.Constant-power load system stabilization by passive damping ［J］.IEEE Transactions on Power Electronics，2011，26（7）：1832-1836.

［16］RADWAN A A A，MOHAMED Y A I.Linear active stabilization of converter-dominated DC microgrids［J］.IEEE Transactions on Smart Grid，2012，3（1）：203-216.

［17］李玉梅，查晓明，刘飞，等.带恒功率负荷的直流微电网母线电压稳定控制策略［J］.电力自动化设备，2014，34（8）：57-64.LI Yumei，ZHA Xiaoming，LIU Fei，etal.Stability control strategy for DC microgrid with constant power load［J］.Electric Power Automation Equipment，2014，34（8）：57-64.

［18］LIUTANAKULP，AWAN A，PIERFEDERICIS，etal.Linear stabilization of a DC bus supplying a constant power load：a general design approach ［J］.IEEE Transactionson Power Elec-tronics，2010，25（2）：475-488.

［19］TAHIM A P N，PAGANO D J，LENZ E，et al.Modeling and stability analysis ofislanded DC microgrids under droop control［J］.IEEE Transactions on Power Electronics，2010，25（2）：475-488.

［20］EMADI A，FAHIMI B，EHSANI M.On the concept of negative impedance instability in advanced aircraft power systems with constant power loads［C］∥34th Intersociety Energy Conversion Engineering Conference.Vancouver，BC，Canada：［s.n.］，1999：1-11.