适应于时变频率的高精度测频算法设计与实现

袁石良 ，董 杰 ，徐志强 ，朱启晨 ，杨志贤

（1.中国矿业大学（北京）化学与环境工程学院，北京 100083；2.北京四方继保自动化股份有限公司，北京 100085；3.四方继保（武汉）软件有限公司，湖北 武汉 430223）

0 引言

频率是反映电力系统安全稳定运行和电能质量的重要指标，也是系统运行的主要控制参数之一。在水电厂以及风电、光伏等新能源系统中，频率有可能是非恒定、随时间变化的［1］。例如，在发电机并网前，频率随发电机转速增加而增加，并逐渐向系统频率靠拢；系统扰动或发生短路故障时，频率可能会快速下滑［2］；在孤岛运行状态下，频率会有一定程度的波动。频率的波动不但影响测量准确性，甚至可能引起保护装置误动、拒动［3］。

在水电厂及新能源系统中，频率测量主要是由嵌入式保护及测控装置实现。测频方法主要有硬件测频和软件测频。软件测频由于易实现、使用灵活，在嵌入式装置中获得了广泛应用。根据水电厂及新能源系统中频率随时间变化的特点，其对软件测频算法的要求与其他情况下的频率测量要求有所不同，主要包括：在频率偏离额定频率，并且信号中含有谐波、直流、噪声等分量时，均能精确测频；计算量不能太大，不占用或少占用内存为佳；较快的动态跟踪能力，测量时滞小。由于水电厂及新能源系统频率具有随时间变化的特点，如果不能快速、实时、准确地测量频率，或者频率测量时滞过大，都将会影响低频保护、距离保护等功能，以及电厂自动准同期等功能的可靠性。

目前嵌入式装置中常用的软件测频方法主要有基于离散/快速傅里叶变换（DFT/FFT）的测频算法和过零点测频算法。

基于DFT的传统测频算法存在频谱泄漏和栅栏效应［4-5］，测频精度很低，受高次谐波的影响大。各种改进算法中，加窗函数修正DFT测频算法［6-8］的实时性不能满足要求［9］；插值和迭代相结合的DFT测频算法［10］计算量太大，限制了其应用范围。

过零点算法是通过测量信号波形相继过零点间的时间宽度来计算频率［11］。该方法原理简单、计算量小，但容易受高次谐波、直流分量和噪声的影响。文献［12］提出了一种改进的过零点算法，使用傅里叶级数的基波实部或虚部的2个同方向变化的过零点之间的时间差来测量频率，该方法在一定程度上抑制了谐波和直流分量的影响，但是测频精度不高，计算量较大。

上述算法均存在以下2个问题：算法成立的前提条件是信号频率恒定不变，当频率波动或快速变化时测频误差较大；所计算出的频率实际上是数据窗内的平均频率，而不是某一确定时刻的频率。当频率快速变化时，测频误差除了原有算法误差以外，还会有响应速度慢而带来的时滞误差，从而使得测频误差大幅增加。采用频率跟踪并自适应调整采样间隔或调整数据窗长度的技术可实现较高精度的测频［13］，但对嵌入式装置的软硬件方面要求较高，因而限制了其应用范围。文献［14］考虑了频率变化率带来的相邻周期相角差的影响，提出了一种改进算法，但该算法仅适用于频率为（50±3）Hz、频率变化率不超过±5 Hz/s的情况。而在实际系统中，发电机开机过程的频率与50 Hz相去甚远，电力系统故障时频率变化率可能会达到20 Hz/s。因此，该算法的适用范围受到一定的限制。

本文以频率按一定变化率随时间变化为前提，提出了一种软件过零点测频算法，解决了频率时变条件下的精确测频问题。该算法可求出任意采样点时刻频率的实时值，具有计算量小、测频精度高、测频范围大、适用面广、占用内存少等优点，能很好地满足电力系统保护及测控装置的测频需要。

1 算法原理

1.1 任意时刻的频率f与周期T的关系

设待测信号的幅值为A，频率为f，相位角为φ（f，t），则该信号可表示为：

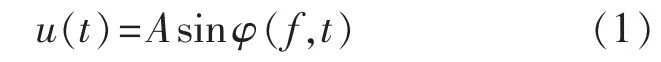
如果频率f非恒定，其一阶导数不为0，则任意时刻 t的相角 φ（f，t）可按下式计算［15］：

其中，ω=2πf为角频率；dω/dt为角加速度。 t=0时刻的初始相角为φ0，初始角速度为ω0=2πf0，初始频率为f0。

考察连续3个过零点处的相位角，如图1所示，将纵坐标移到过零点0处，则t=0时过零点0处相角为0，频率为f0，过零点1和过零点2处的相位角分别为2π和4π。

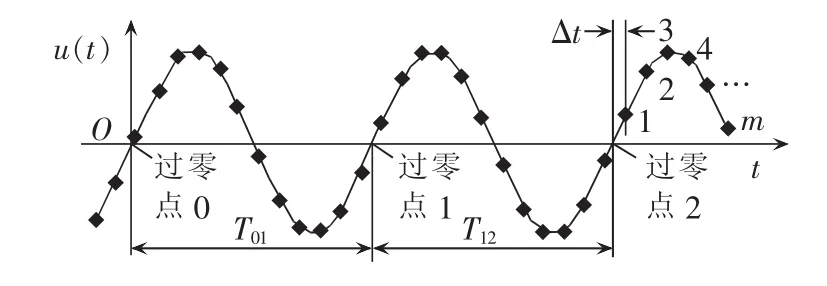
图1 信号波形及过零点示意图Fig.1 Schematic diagram of signal waveform and zero-crossing points

故根据式（2）有：

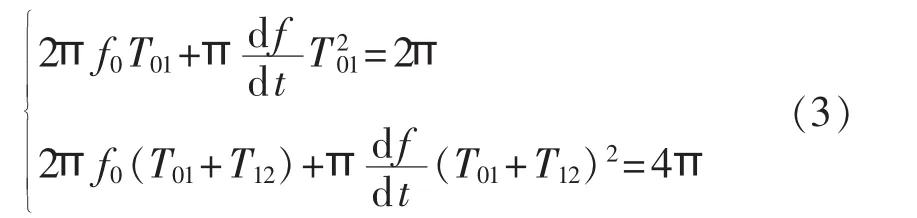
解此方程组，得：

其中，

在求出T01和 T12后（见下节），即可根据式（4）、（5）求出 df/dt和过零点 0 处的频率 f0。

利用上述结果可以求出任意时刻的频率。如图1所示，设最新的过零点为过零点2，当前时刻的采样点为m，采样点m与过零点2中间有m个采样值，则当前时刻的频率为：

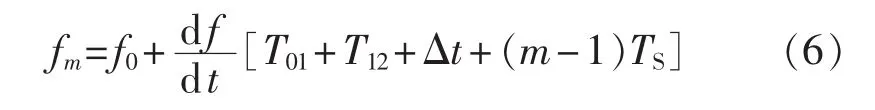
其中，Δt为过零点2与采样点1之间的时间；TS为采样时间间隔。

1.2 周期T的计算

式（4）—（6）中需要用到过零点之间的时间，即周期T。本文按以下方法计算周期T。

1.2.1 计算Δt

如图1所示，信号的过零点通常并不正好是采样点，因此需要求出过零点与过零点后第1个采样点之间的时间Δt，才能准确计算出周期T。

信号的真实过零点无法直接求出，但可以拟合过零点附近的信号波形，求出拟合波形的过零点，从而求出 Δt。

传统过零点算法［11］假定信号波形在过零点附近的波形近似为直线，采用线性插值（或相似三角形）方法求取Δt。为了获得更高的计算精度，本文采用Newton三次插值多项式f（λ）来逼近：

下面分析计算式（7）中的系数a0—a3。

参见图2，根据等距节点Newton三次插值多项式公式，取过零点前后4个采样点：过零点后第1个采样点（tk，uk），过零点之前 3 个采样点（tk-1，uk-1）、（tk-2，uk-2）、（tk-3，uk-3）。 利用这 4 个采样值建立向后差分表，如表1所示。

图2 Newton三次插值多项式计算示意图Fig.2 Schematic diagram of Newton cubic interpolation polynomial calculation

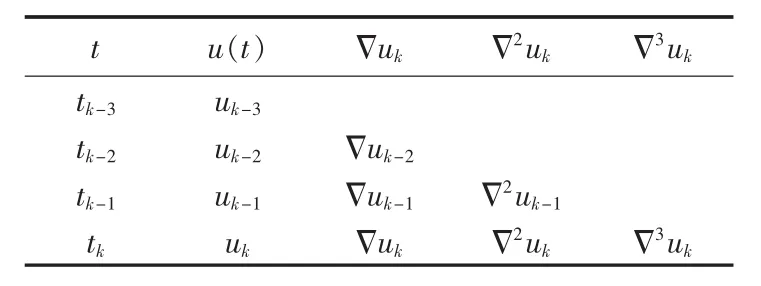
表1 Newton向后差分表Table 1 Newton backward differential table

表1中，

Newton三次插值多项式函数为：

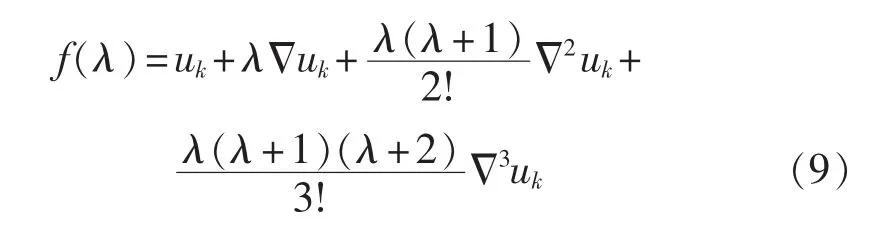
其中，λ与Δt的关系为：

根据式（9）可求出式（7）的系数如下：

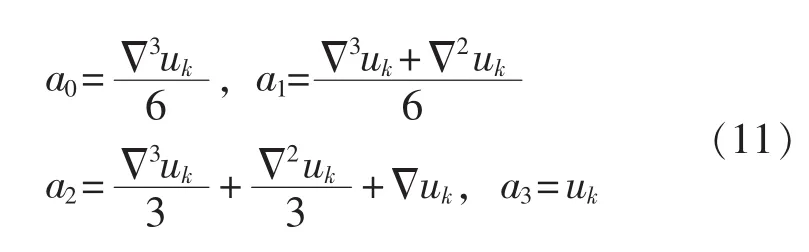
令式（7）中 f（λ）=0，求拟合函数的过零点：

采用Newton迭代法求上式的根：

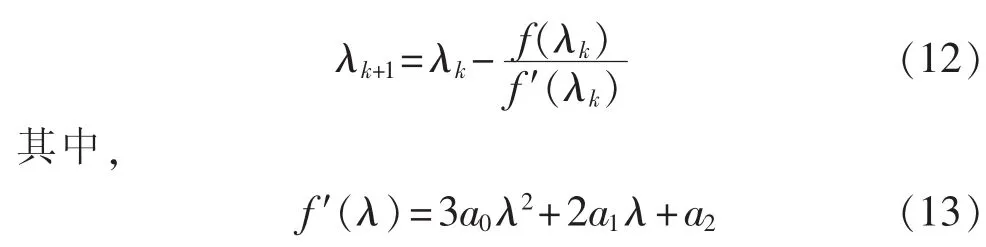
迭代初值λ0可根据三角形相似法求得。参见图2，根据相似三角形原理，有：

将 Δt=-λTS代入上式，得，故取迭代初值：

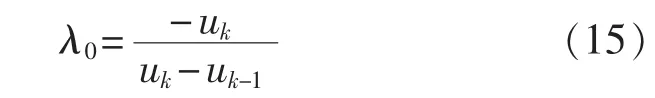
一般迭代计算2次即可。计算出λ后，即可计算出 Δt=-λTS。

1.2.2 计算周期T

设相邻2个过零点之间的采样点数为N，则周期T为：

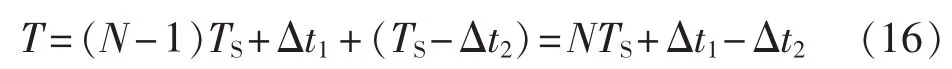
其中，Δt1、Δt2分别为前后2个过零点距离过零后第1个采样点之间的时间。

2 算法实现步骤

a.寻找过零点。程序从当前采样点向前逐个搜索，直到找到某个采样点为正数，而前一个采样点为负数，则由负到正过零点必在2个采样点之间。

b.根据式（8）、式（11）计算拟合函数系数。

c.计算过零点。根据式（15）计算迭代初值，利用式（7）、（12）、（13）迭代计算得到过零点处的 λ 值。

d.计算当前周期T。用式（10）计算出当前过零点的Δt并保存，利用式（16）计算出当前的周期T并保存。

e.计算当前采样点处的频率。利用最近3个过零点处的 Δt和周期 T，用式（4）、（5）求出 df/dt和过零点0处的频率f0，用式（6）计算出当前频率。

3 算法仿真

对各种情况下的算法性能进行仿真以验证其测频精度，并与文献［10］的改进DFT算法和文献［12］的改进过零点算法进行了对比，频率计算误差取自对应文献中给出的结果。

3.1 纯正弦波

设电压信号为 u（t）=Asin（2πft+φ），频率取 30～70 Hz，初相角随机选择。取30周期计算结果中误差最大值，测量结果见表2。

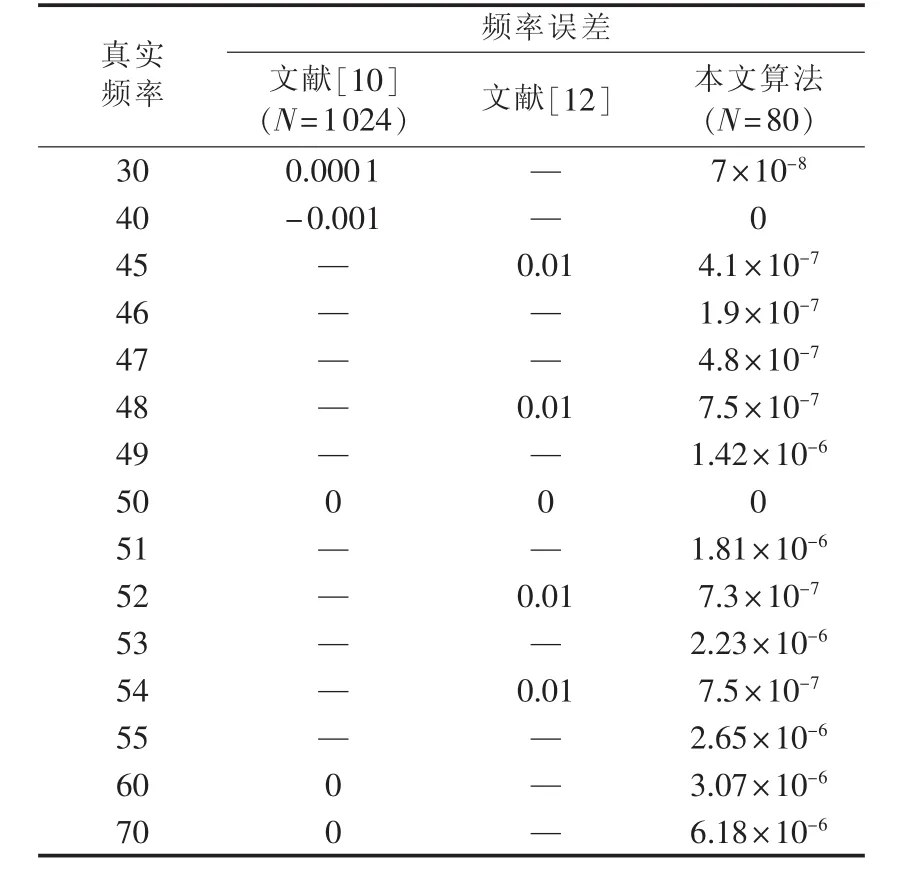
表2 纯正弦信号时的频率误差Table 2 Frequency error of pure sine signal Hz

从表2可见，本文算法的最大误差为10-6Hz级。

3.2 叠加谐波、噪声

设电压信号为：基波幅值100 V，2次谐波10%，3次谐波20%，5次谐波10%，7次谐波5%，固有直流10%，噪声信号取50 dB高斯白噪声。频率取45～55 Hz，初相角随机选择。取30周期计算结果中误差最大值，测量结果见表3。

表3 含有谐波和噪声时的频率误差Table 3 Frequency error of signals with harmonics and noise Hz

从表 3 可见，改进 DFT［10］和改进过零点算法［12］对谐波、固有直流分量和噪声有一定抑制作用，最大误差分别为-0.0156 Hz和0.02 Hz，而本文算法的最大误差仅为0.0024 Hz。因此，本文算法可在一定程度上降低上述因素的影响。

3.3 频率波动

模拟发电机启机阶段频率快速变化。取初始频率 30 Hz，初相角 -10°，频率变化率 df/dt=10 Hz/s。则频率及输入电压信号模型为：

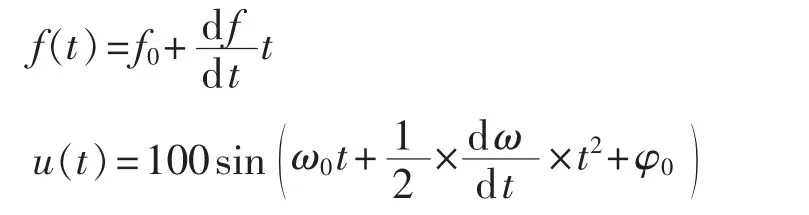
其中，ω0=2πf0；ω=2πf。

仿真结果见表4。从表4可见，本文算法在频率波动时测频精度较高，最大误差仅为10-6Hz级。

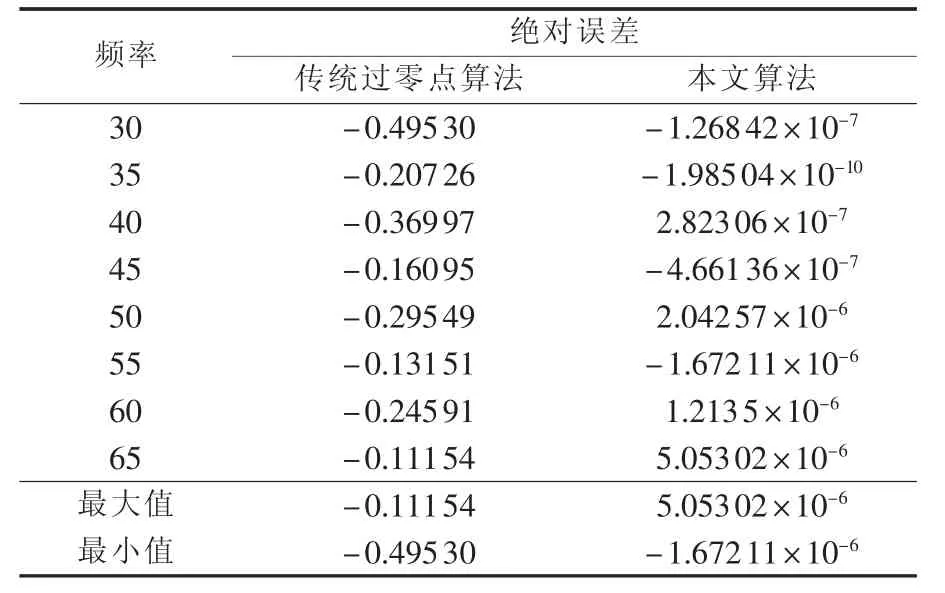
表4 频率波动时的频率误差Table 4 Frequency error during frequency fluctuation Hz

3.4 频率非线性波动

在实际运行过程中，频率有可能非线性变化，即频率的二阶导数非零。本文对此情况也进行了仿真。 取初始频率 30Hz，初相角 -10°，df/dt=10Hz/s，d2f/dt2=1 Hz/s2。则频率及电压信号模型为：

仿真结果见表5。从表5可见，当频率的一阶导数为10 Hz/s，且频率的二阶导数高达1 Hz/s2时，本文算法仍有较高精度，最大误差仅为10-4Hz级，可以满足水电厂和新能源系统的测频需要。

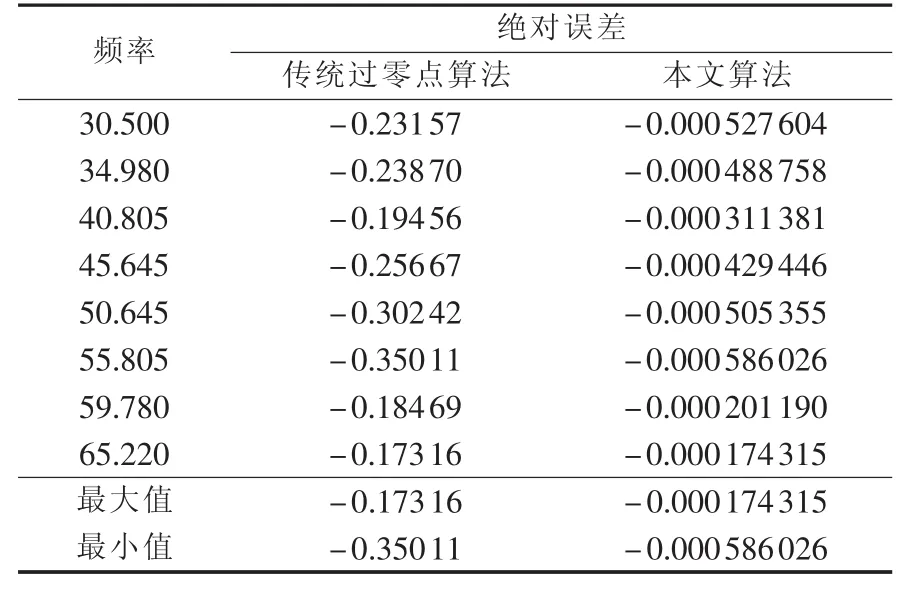
表5 频率非线性波动时的频率误差Table 5 Frequency error during frequency nonlinear variation Hz

4 结论

本文根据相邻过零点的相位关系，在频率随时间变化条件下，推导出了任意时刻频率的计算公式，并综合运用了牛顿三次插值多项式、牛顿迭代法、三角形相似法等来精确求解相邻过零点之间的周期时间。本文算法计算量很小，仅需要28次乘除法、32次加减法。

MATLAB仿真表明，本文算法在频率波动甚至非线性变化时，测频精度可高达10-4Hz级；而在纯正弦波时的测频精度高达10-6Hz级；即使存在谐波和噪声，测频精度也可高达10-3Hz级。因此，本文算法具有测频精度高、测频范围大、适用面广、计算量小、占用内存少等优点，解决了频率时变条件下测频算法误差大的问题，并在一定程度上降低了高次谐波、直流分量和噪声的影响，可以满足电力系统各种保护和测控装置测频需要。

本文推导出的频率与周期的关系式也可应用于硬件测频等其他测频算法中。

［1］潘伟，李勇，曹一家，等.用于大规模集中式风电并网的 VSCHVDC 频率控制方法［J］.电力自动化设备，2015，35（5）：94-99.PAN Wei，LI Yong，CAO Yijia，et al.Frequency control of gridconnection system based on VSC-HVDC for large-scale centralized wind farm［J］.Electric Power Automation Equipment，2015，35（5）：94-99.

［2］薄其滨，王晓茹，刘克天.基于v-SVR的电力系统扰动后最低频率预测［J］.电力自动化设备，2015，35（7）：83-88.BO Qibin，WANG Xiaoru，LIU Ketian.Minimum frequency prediction based on v-SVR for post-disturbance power system［J］.Electric Power Automation Equipment，2015，35（7）：83-88.

［3］蔡海青，黄立滨，郭琦，等.直流孤岛运行方式下交流保护装置频率适应性仿真研究［J］.电力自动化设备，2016，36（3）：169-174.CAI Haiqing，HUANG Libin，GUO Qi，etal.Simulation of frequency adaptability for AC protective equipment in islanding mode of HVDC operation［J］.Electric Power Automation Equipment，2016，36（3）：169-174.

［4］庞浩，李东霞，俎云霄，等.应用FFT进行电力系统谐波分析的改进算法［J］.中国电机工程学报，2003，23（6）：50-54.PANG Hao，LI Dongxia，ZU Yunxiao，et al. An improved algorithm forharmonic analysisofpowersystem usingFFT technique［J］.Proceedings of the CSEE，2003，23（6）：50-54.

［5］张伏生，耿中行，葛耀中.电力系统谐波分析的高精度FFT算法［J］.中国电机工程学报，1999，19（3）：63-66.ZHANG Fusheng，GENG Zhongxing，GE Yaozhong.FFT algorithm with high accuracy for harmonic analysis in power system ［J］.Proceedings of the CSEE，1999，19（3）：63-66.

［6］柴旭峥，文习山，关根志，等.一种高精度的电力系统谐波分析算法［J］.中国电机工程学报，2003，23（9）：67-70.CHAI Xuzheng，WEN Xishan，GUAN Genzhi，et al.An algorithm with high accuracy for analysis of power system harmonics［J］.Proceedings of the CSEE，2003，23（9）：67-70.

［7］侯启方，李艳鹏，刘承志.基于插值FFT算法的电力系统频率高精度测量［J］.电气应用，2007，26（6）：99-102.HOU Qifang，LI Yanpeng，LIU Chengzhi.Power system frequency high-accuracy measurement based on interpolated FFT algorithm［J］.Electrotechnical Application，2007，26（6）：99-102.

［8］许珉，王玺，程凤鸣.基于加Hanning窗递推DFT算法的测频方法［J］.电力自动化设备，2010，30（11）：73-74，78.XU Min，WANG Xi，CHENG Fengming.Frequencymeasuring based on Hanning windowed recursive DFT algorithm［J］.Electric Power Automation Equipment，2010，30（11）：73-74，78.

［9］卞星明，文远芳，雷琴.电力系统测频算法比较［J］.高电压技术，2006，32（5）：111-114.BIAN Xingming，WEN Yuanfang，LEI Qin.Comparison on power system frequency measurement algorithm［J］.High Voltage Engineering，2006，32（5）：111-114.

［10］李一泉，何奔腾.一种基于傅氏算法的高精度测频方法［J］.中国电机工程学报，2006，26（2）：78-81.LI Yiquan，HE Benteng.A high-accuracy algorithm for measuring frequency of power system based on Fourier filter［J］.Proceedings of the CSEE，2006，26（2）：78-81.

［11］苑鸿，侯思祖，张同良.远动信号频率的测量方法与实现研究［J］.华北电力大学学报（自然科学版），2004，31（2）：80-82.YUAN Hong，HOU Sizu，ZHANG Tongliang.Realization of frequency measurement of remote signals［J］.Journal of North China Electric Power University（Natural Science Edition），2004，31（2）：80-82.

［12］方存洋，陈玉兰，潘汉广.一种实用的软件测频算法［J］.电力自动化设备，2007，27（12）：36-39.FANG Cunyang，CHEN Yulan，PAN Hanguang.Power frequency measurement algorithm［J］.Electric Power Automation Equipment，2007，27（12）：36-39.

［13］张艳霞，陈旭林.基于DFT舶电力系统频率及谐波精确算法［J］.中国电力，2012，45（2）：1-4.ZHANG Yanxia，CHEN Xulin.An accurate DFT based power system frequencyand harmonicsmeasurementalgorithm ［J］.Electric Power，2012，45（2）：1-4.

［14］张同尊，邵俊松，方勇杰.一种基于离散傅里叶变换的频率测量算法［J］.电力系统自动化，2007，31（22）：70-72.ZHANG Tongzun，SHAO Junsong，FANG Yongjie.An algorithm for frequency measurement based on DFT［J］.Automation of Electric Power Systems，2007，31（22）：70-72.

［15］卓乐友，叶念国，翁乐阳，等.微机型自动准同步装置的设计和应用［M］.北京：中国电力出版社，2002：2-8.