基于小波分解与滑动峰态的微弱放电信号联合检测方法

刘卫东，刘尚合

（军械工程学院 电磁环境效应国家级重点实验室，河北 石家庄 050003）

0 引言

目前，在全封闭组合电器（GIS）等电气设备的在线监测和故障诊断中，利用外置接收天线对一定距离范围内的局部放电源进行非接触式探测和定位，受到越来越多的关注并展现了其潜在的优越性［1-5］。

英国Strathclyde大学的P.J.Moore等人在分析局部放电时频域特征的基础上，设计研制了宽带、小型化、高灵敏度的盘锥型测试天线，并在局部放电非接触式探测方面开展了一系列研究工作［6-10］：通过组建固定式［7］、可移动车载式［8］、可移动分布式［9］等变电站局部放电监测系统，对英国国家电网等高压电力平台进行了局部放电源的远距离监测实验，初步验证了局部放电非接触式探测技术在实际工程应用中的可行性。在国内，重庆大学、上海交通大学等单位也相继开展了局部放电非接触式监测和早期预警的研究工作：重庆大学的姚陈果等人［11］利用4个安装在楼顶的宽带盘锥天线实现了对水平距离约35 m处变电站内局部放电源的探测；上海交通大学的侯慧娟等人［4］利用4个宽带全向天线，在某500 kV变电站内通过对模拟局部放电源进行试验测试，实现了对10 m范围内局部放电源的空间定位。

在非接触式局部放电监测系统的实际工程应用中，随着测试距离增大，在背景噪声干扰等因素的影响下，实测局部放电信号的信噪比SNR（Signal to Noise Ratio）往往都比较低，甚至完全淹没在背景噪声和干扰中。因此，研究低信噪比条件下微弱放电信号的检测和处理方法，进一步拓展非接触式测试技术的覆盖范围及其潜在优势等具有重要意义。在信号处理方面，四阶累积量即峰态在抑制高斯噪声、反映非高斯信号特性方面有显著优势，已在微弱振动冲击信号的处理中得到成功应用［12-13］，而局部放电产生的电磁辐射信号本身也具有典型的非平稳、非高斯特性［14］。

基于上述考虑，本文在分析滑动峰态算法检测性能的基础上，提出了基于小波分解与滑动峰态相结合的微弱放电信号联合检测方法，改善了现有滑动峰态算法在抗混合噪声干扰等方面的不足，并对其可行性和有效性进行了仿真分析和实验验证。

1 联合检测方法的基本原理

1.1 滑动峰态算法

根据高阶累积量定义，峰态可表示为：

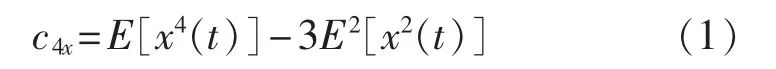
其中，x（t）为采样信号的时间序列。在此基础上，文献［12］提出了一种用于凸显微弱冲击信号特征的滑动峰态算法，其定义为：

其中，i=1，2，…，n；n 为采样点数；cL（ti）为经滑动峰态计算得到的峰态时间序列表示对 x（ti）—x（ti+L-1）L个点计算峰态值并取绝对值；L为滑动窗宽度，其取值对滑动峰态序列的计算结果影响较大。为此，文献［13］提出利用滑动峰态序列的峰态值作为L的取值判据，即取滑动峰态序列的峰态值最大时所对应的L作为最佳的滑动窗宽。本文将采用文献［13］方法作为选择最佳L值的参考依据。

在上述式（2）所示的滑动峰态算法中，L作为滑动窗宽度，其在滑动峰态序列的计算中是固定不变的。而在实际应用中，在利用滑动峰态滤波算法对微弱脉冲信号进行检测时，对于不同类型、甚至同类型不同信噪比的噪声干扰信号，其滑动窗宽度L的最优取值往往存在一定差异，而L的取值又会直接影响滑动峰态序列的计算结果。因此，对于混合噪声干扰信号中的微弱脉冲信号检测，如果继续采用固定的滑动窗宽度对其进行峰态滤波处理，其检测性能往往就会显著劣化，从而无法达到预期的检测效果。针对上述问题，本文提出一种结合小波分解预处理的滑动峰态改进方法，下面就对该方法进行分析讨论。

1.2 联合检测方法及其流程

小波变换是一种时间窗和频率窗都可改变的时频分析方法。通过小波变换可以将混合噪声干扰信号分解到不同的尺度上，从而近似实现对该信号中不同类型混合信号的局部分析和峰态滤波处理，这也是本文所提联合检测方法的基本思路。基于小波分解和峰态滤波的联合检测方法的流程如图1所示（图中 Li（i=1，2，…，N+1）为第 i个重构信号对应的滑动窗宽度），其分析步骤如下。

a.对实测信号进行N层小波分解，并通过小波分解系数对信号的低频和高频部分进行重构。考虑到本文所研究的对象为脉冲信号，其频率分布集中在高频，因此主要对高频部分进行信号重构，并得到d1—dN层共N个高频重构信号和1个aN层低频重构信号。

b.结合最佳滑动窗宽L，对重构得到的aN层低频重构信号和d1—dN层高频重构信号分别进行峰态滤波处理，得到峰态序列caN和cd1—cdN。

c.对峰态序列进行叠加合成，得到对应实测信号的滑动峰态序列c，并通过检测该序列中的脉冲及其峰值所对应位置实现对微弱放电脉冲信号的检测与特征提取。其中，考虑到在计算滑动峰态序列时，受随机噪声干扰等影响会出现L=1的情况，由此得到的计算结果不能反映放电信号的峰态分布特性。因此，在进行峰态序列的合成时，L=1所对应的峰态序列不参与合成计算，这里采用将合成系数k置零的方式来实现。

图1 联合检测方法基本流程Fig.1 Flowchart of joint detection method

在上述步骤a中，对实测信号进行小波分解时，小波基函数的确定可结合待检测脉冲信号的先验知识进行合理选择，这里选择sym8小波基函数对放电信号进行小波分解［15］。在确定小波分解层数时，通过后期的仿真分析和实验验证发现，在小波分解达到一定层数后，随着分解层数的继续增加，由图1所示流程合成得到的峰态序列c基本保持恒定不变，此时的分解层数即可视为满足联合检测的最小且最优分解层数。

2 仿真分析

以检测微弱局部放电电磁辐射产生的脉冲信号为例，采用双指数衰减振荡波形模拟仿真放电脉冲信号，结果如图 2（a）所示。 图 2（a）中，信号的采样频率设置为2 GHz，采样时间长度设置为1 μs，峰峰值约为8.8 mV，放电时刻设置在第400 ns处。为模拟混合噪声干扰的影响，对图2（a）中的局部放电仿真信号分别叠加高斯白噪声（SNR=-10dB）和周期性窄带干扰信号，结果如图2（b）所示。其中，为模拟广播通信等周期性窄带干扰信号对放电信号测试的影响，图2（b）中叠加了具有如下形式的窄带干扰信号：

其中，A、B均为干扰信号幅值，此处设置A=2 mV、B=5 mV；f1、f2和f3为干扰信号频率，此处分别设置f1=80 MHz、 f2=110 MHz、 f3=250 MHz。

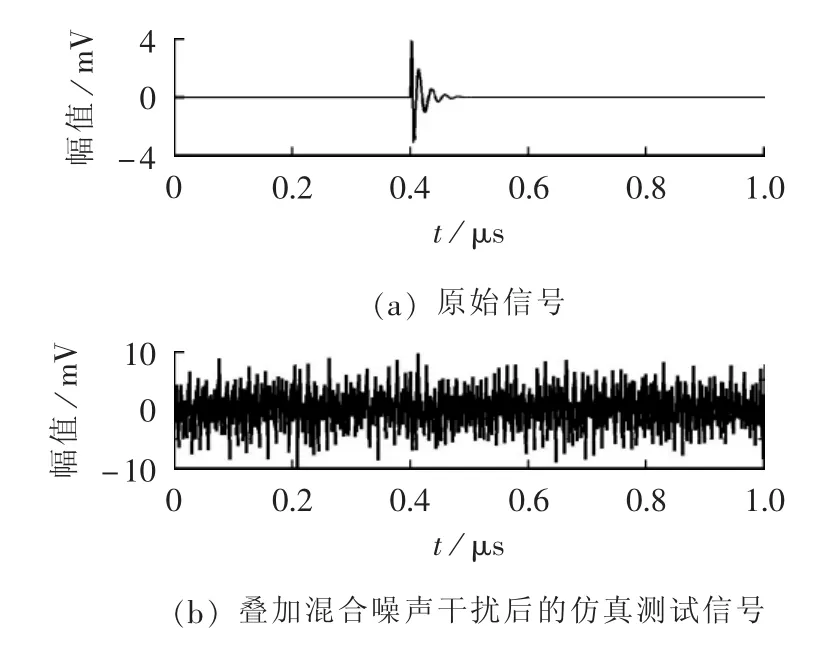
图2 局部放电仿真信号Fig.2 Simulated partial discharge signals

从图2（b）中可以看出，叠加噪声干扰后所形成的仿真测试信号的信噪比比较低，放电脉冲信号基本处于被噪声干扰淹没的状态，从其时域波形上很难明显判断是否有放电信号存在，也无法准确提取放电脉冲信号的发生时刻等特征信息。对图2（b）所示仿真测试信号进行滑动峰态滤波，结果见图3。

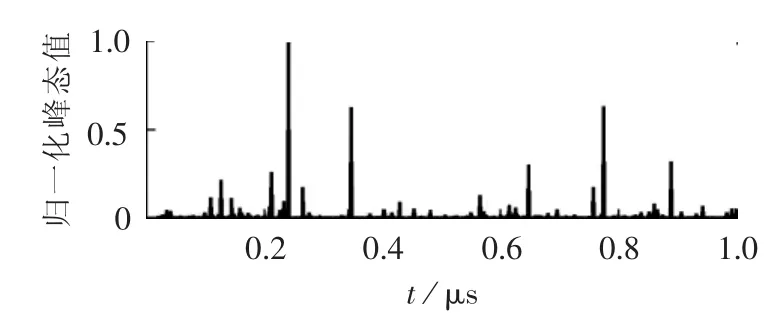
图3 混合噪声干扰下放电信号的峰态检测结果（L=1）Fig.3 Results of kurtosis detection for partial discharge signals with mixed noises（L=1）

从图3中可以看出，经峰态滤波后，其对应的峰态时间序列中出现了多个明显的脉冲特征，且最大脉冲的峰值对应时刻为239 ns，这与图2（a）中的仿真设置明显不符，即在仿真设置的混合噪声干扰下，采用固定滑动窗宽度的峰态滤波算法没有实现对放电脉冲信号的检测。

利用本文提出的联合检测方法对图2（b）所示仿真测试信号进行分析处理，结果如图4所示。从图4（c）中可以看出，基于联合检测合成的峰态序列中出现了明显的脉冲特征信号，且最大脉冲的峰值对应时刻为401 ns，与图2（a）中仿真信号所设置的放电发生时刻基本相符，实现了对放电脉冲信号的检测，这也说明在复杂背景噪声干扰下，本文所提联合检测方法相比于采用固定滑动窗宽度的现有滑动峰态算法，在微弱放电信号的检测中具有明显优势。

从图4（b）中可以看出，对不同尺度的小波重构信号进行峰态滤波时，滑动窗宽度L的最优取值存在较大差异，而正是由于这种差异性才使得微弱放电脉冲信号所表现的峰态特征得以从噪声和干扰中分离并凸显出来，但这种差异性在采用固定滑动窗宽度对混合信号进行处理时却无法得以体现，这也正是现有滑动峰态算法在面临混合噪声干扰时其检测性能会显著劣化的一个主要原因。

为进一步验证本文所提联合检测方法的优越性，在保持局部放电仿真信号幅值不变的情况下，继续增大图2（b）中噪声和干扰信号的强度。其中，叠加高斯白噪声后所形成的仿真测试信号，其信噪比由原来的-10 dB降低至-15 dB；根据式（3）将周期性窄带干扰信号的幅值增大为原来的3倍，即设置A=6 mV、B=15 mV，其他参数设置不变。对增大混合噪声干扰后的仿真测试信号进行滑动峰态处理，结果如图5所示。其中，图5（a）采用的是固定滑动窗宽度的峰态算法；图5（b）采用的是本文提出的联合检测方法。

对比图5（a）与图3可见，随着噪声干扰强度的进一步增大，现有滑动峰态算法的检测性能进一步劣化，无法准确实现对微弱放电信号的检测；对比图5（b）与图 4（c）可见，在大幅增加混合噪声干扰的强度后，通过联合检测方法处理得到的峰态序列虽然在一定程度上也受到了噪声干扰的影响，但也出现了比较明显的脉冲特征信号，且最大脉冲的峰值对应时刻为401 ns，与图2（a）中仿真信号所设置的放电发生时刻基本相符，从而实现了对微弱放电信号的准确检测。

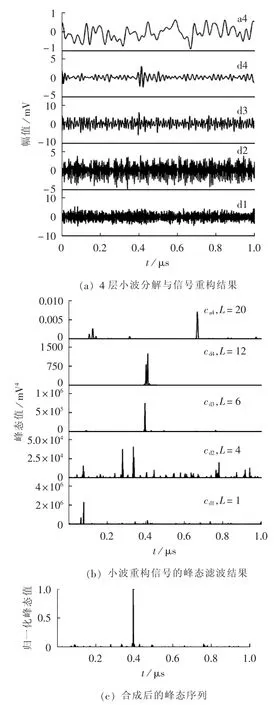
图4 混合噪声干扰下放电信号的联合检测结果Fig.4 Results of joint detection for partial discharge signals with mixed noises

综合上述对比分析可见，本文所提联合检测方法，通过小波分解预处理对信号进行局部分析和细化，实现了在同一个信号内部利用多个滑动窗宽度进行“区别性对待、针对性处理”的优化检测方案，其检测性能相比于采用固定滑动窗宽度的现有峰态算法有显著提升，从而有利于在复杂背景噪声干扰和低信噪比下实现对微弱放电脉冲信号的检测和特征提取。

图5 增大噪声干扰后的放电信号检测结果Fig.5 Results of detections for partial discharge signals with amplified noises

3 实验分析

在对局部放电产生的电磁辐射信号进行实际测试时，由于无法预知放电信号的真实发生时刻，因此为确保联合检测后的分析结果与真实的放电信号具有明确的对应关系，本文采用真实放电信号与实测噪声干扰信号相叠加的方式来模拟低信噪比条件下的实测数据。即在实测环境条件下，先利用接收天线采集背景噪声和干扰信号n（t），然后开启局部放电源并在距离其较近处采集真实放电信号s（t），最后将 s（t）乘衰减系数 g（0≤g≤1）并与 n（t）进行叠加得到模拟的实测数据 f（t），即：

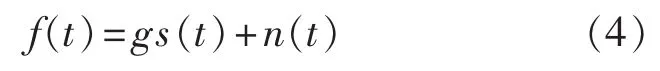
其中，衰减系数g可近似表征远距离测试中不同因素所导致的真实放电信号强度衰减。

通过对f（t）进行小波分解和峰态滤波联合检测并将分析结果与s（t）进行对比，可近似检验该联合检测方法在实测环境下的准确性和有效性。

图6是利用对数周期天线在实测环境下测试得到的背景噪声干扰信号和高压局部放电模拟源产生的电磁辐射信号，采样频率均为2 GHz，采样时间为 2 μs。

由图6（b）可见，近距离实测得到的放电信号峰值约为108 mV。为模拟远距离测试条件下该放电信号的强度衰减，根据式（4）将衰减系数g设置为0.1，则衰减后的信号峰值约为10.8 mV，将其与图6（a）所示的噪声干扰信号相叠加，结果如图7所示。由于衰减后的放电信号强度明显弱于噪声干扰信号强度，因此两者叠加后可近似模拟低信噪比条件下的实测数据。从图7中也可以明显看出，实测得到的放电信号已被完全淹没在背景噪声干扰中。

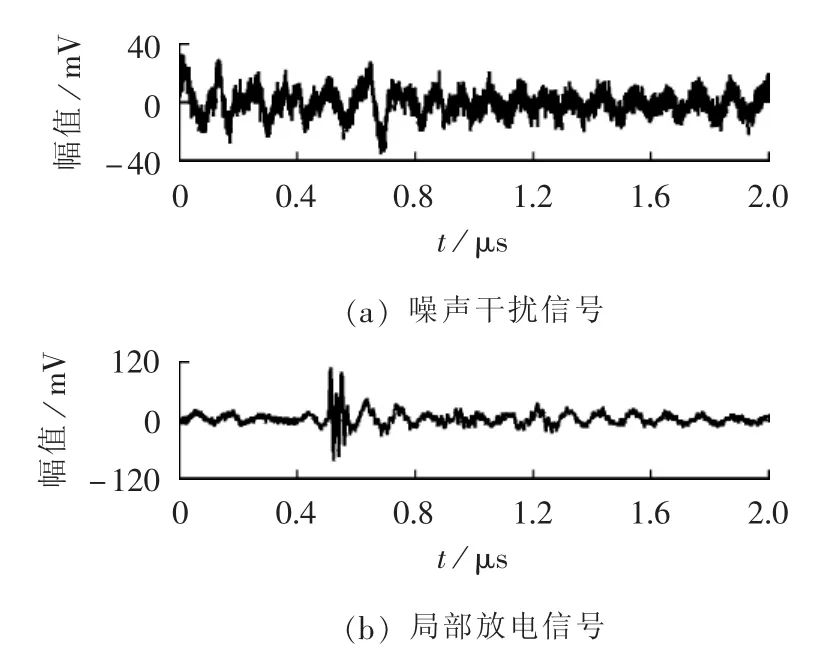
图6 实测噪声干扰与放电信号的时域波形Fig.6 Measured time-domain waveforms of noises and discharge signals

图7 模拟产生的低信噪比波形Fig.7 Simulated waveform with low SNR

利用本文提出的联合检测方法对图6（b）所示的放电信号和图7所示的模拟实测数据分别进行分析处理，归一化之后的对比结果如图8所示。图中，①对应的是图6（b）所示放电信号的联合检测结果，其中小波分解为4层；②对应的是图7所示模拟实测数据的联合检测结果，其中小波分解为6层；③对应的是利用固定滑动窗宽度峰态算法对图7所示模拟实测数据的检测结果（L=3）。

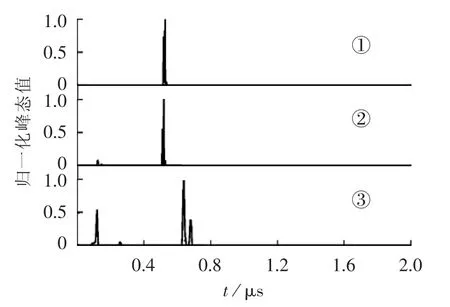
图8 模拟及实测波形检测结果对比Fig.8 Comparison of detection results

对比图8中①、②，利用联合检测方法对图6（b）和图7所示信号处理得到的峰态序列中，均有明显的脉冲特征信号，且最大脉冲的峰值对应时间均为526 ns，即在模拟低信噪比实测环境下，利用联合检测方法实现了对微弱放电信号的检测；而从图8中③可见，受背景噪声干扰的严重影响，利用现有滑动峰态算法处理得到的峰态序列中出现了多个明显的脉冲特征信号，且最大脉冲的峰值对应时刻为644ns，与图6（b）中实测放电信号的发生时间明显不符，即其没有实现对放电信号的检测。上述对比也进一步说明，本文所提联合检测方法具有较强的抗噪声干扰能力，可用于在复杂背景噪声干扰下对微弱放电信号进行检测。

4 结论

a.滑动峰态算法对非高斯信号具有很好的表征能力，但由于滑动窗宽度L的选择对峰态序列的计算结果影响较大，而L的最佳取值又与待处理信号的类型、信噪比等因素密切相关，因此当采用固定滑动窗宽度L来处理混合噪声干扰下的微弱放电脉冲信号时，滑动峰态算法的检测性能往往会显著劣化，从而不利于其在低信噪比条件下实现对微弱放电脉冲信号的准确检测。

b.针对上述问题，本文将小波分解与峰态滤波算法相结合，提出了一种改进的微弱放电信号联合检测方法，该方法可使用多个优化的滑动窗宽度对实测信号进行差异化分析和处理，显著提高了其抗噪声干扰的能力。仿真和实验结果表明：相比采用固定滑动窗宽度的峰态算法，所提联合检测方法在低信噪比条件下的检测性能明显提升，适用于对复杂背景噪声干扰下的微弱放电信号进行检测，对进一步提升现有非接触式局部放电测试系统的探测能力具有一定的参考意义。

［1］AMIN E M，KARMAKAR N C.A passive RF sensor for detecting simultaneous partial discharge signals using time-frequency analysis［J］.IEEE Sensors Journal，2016，16（8）：2339-2348.

［2］ZHANG Y，UPTON D，JABER A，et al.Multiple source localization for partial discharge monitoring in electrical substation［C］∥2015 Loughborough Antennas&Propagation Conference（LAPC）.Loughborough，UK：［s.n.］，2015：1-4.

［3］BLE F Z，LEHTONEN M，KIM C.Novel approach of arcing faults electromagnetic radiated energy source location using antennas in power systems［J］.International Review of Electrical Engineering（IREE），2014，9（5）：1049-1059.

［4］侯慧娟，盛戈皞，苗培青，等.基于超高频电磁波的变电站局部放电空间定位［J］.高电压技术，2012，38（6）：1334-1340.HOU Huijuan，SHENG Gehao，MIAO Peiqing，et al.Partial discharge location based on radio frequency antenna array insubstation［J］.High Voltage Engineering，2012，38（6）：1334-1340.

［5］曾韵梅，陈攀，周电波.非接触式局部放电检测天线的设计和优化研究［J］.华中电力，2012，25（3）：67-71.ZENG Yunmei，CHEN Pan，ZHOU Dianbo.Design and optimization study of detection antenna for noncontact partial discharge ［J］.Central China Electric Power，2012，25（3）：67-71.

［6］MOORE P J，PORTUGUES I，GLOVER I A.A nonintrusive partial discharge measurement system based on RF technology［C］∥IEEE PowerEngineering Society GeneralMeeting.Toronto，Canada：IEEE，2003：628-633.

［7］MOORE P J，PORTUGUES I E，GLOVER I A.Partial discharge investigation of a power transformer using wireless wideband radio-frequency measurements［J］.IEEE Transactions on Power Delivery，2006，21（1）：528-530.

［8］JUDD M D.Radiometric partial discharge detection［C］∥InternationalConference on Condition Monitoring and Diagnosis.Beijing，China：IEEE，2008：1025-1030.

［9］PORTUGUES I E，MOORE P J，GLOVER I A，et al.A portable wideband impulsive noise location system［J］.IEEE Transactions on Instrumentation and Measurement，2008，57（9）：2059-2066.

［10］HARRIS R M，JUDD M D，MOORE P J，et al.Radiometric detection and analysis of arcing faults［J］.IEEE Transactions on Dielectrics and Electrical Insulation，2015，22（3）：1547-1558.

［11］姚陈果，周电波，陈攀，等.采用超高频法监测变电站设备局放水平及其早期预警［J］.高电压技术，2011，37（7）：1670-1676.YAO Chenguo，ZHOU Dianbo，CHEN Pan，etal.UHF-based monitoring for equipment PD within the substation and early warning［J］.High Voltage Engineering，2011，37（7）：1670-1676.

［12］杨富春，周晓军，张志刚.基于滑动峰态算法的信号弱冲击特征提取及应用［J］.振动与冲击，2009，28（4）：103-109.YANG Fuchun，ZHOU Xiaojun，ZHANG Zhigang.A new method for extracting weak impulse characteristic based on a sliding kurtosis algorithm［J］.Journal of Vibration and Shock，2009，28（4）：103-109.

［13］张志刚，石晓辉，陈哲明，等.基于改进EMD与滑动峰态算法的滚动轴承故障特征提取［J］.振动与冲击，2012，31（22）：80-83.ZHANG Zhigang，SHIXiaohui，CHEN Zheming，etal.Fault feature extraction of rolling element bearing based on improved EMD and sliding kurtosis algorithm［J］.Journal of Vibration and Shock，2012，31（22）：80-83.

［14］刘卫东，刘尚合，胡小锋.电晕放电电磁辐射信号的双谱估计与时频分析［J］.高压电器，2010，46（5）：26-29.LIU Weidong，LIU Shanghe，HU Xiaofeng.Bispectrum estimation and time-frequency analysis of electromagnetic signal radiated from corona discharge［J］.High Voltage Apparatus，2010，46（5）：26-29.

［15］高圣伟，张牧，袁臣虎，等.变压器局部放电信号分析中小波基函数的选择和比较［J］.天津工业大学学报，2011，30（3）：72-75.GAO Shengwei，ZHANG Mu，YUAN Chenhu，et al.Comparison and choice of wavelet basis function in wavelet analysis of partial discharge signal［J］.Journal of Tianjin Polytechnic University，2011，30（3）：72-75.