拓扑群范畴研究的若干进展

贺 伟

(南京师范大学 数学科学学院, 江苏 南京 210046)

拓扑群范畴研究的若干进展

贺 伟

(南京师范大学 数学科学学院, 江苏 南京 210046)

拓扑群是拓扑代数领域的重要研究对象，在调和分析、动力系统等领域有广泛的应用.拓扑群和连续群同态范畴具有许多重要且有趣的性质.介绍从范畴论角度研究拓扑群范畴的若干进展.内容涉及拓扑群范畴的基本性质、拓扑群范畴的准紧反射、紧反射(Bohr紧化)、Raǐkov完备反射(Raǐkov完备化)、C-紧拓扑群、c-完备态射等.

拓扑群; 连续群同态; 准紧群; 紧群; C-紧群; c-proper同态; Raǐkov完备群

一个拓扑群是一个群(G,+)使得G同时是一个拓扑空间，并且加法运算+:G×G→G和逆运算-:G→G均连续.拓扑群是拓扑代数领域的重要研究对象，在调和分析、动力系统等领域有广泛的应用.关于拓扑群和连续群同态范畴性质的研究可以追溯到20世纪40年代，A. A. Markov[1]证明了任意给定拓扑空间上的自由拓扑群的存在唯一性，并用范畴论语言证明了Hausdorff拓扑群范畴到拓扑空间范畴的遗忘函子存在左伴随，并且当限制到完全正则空间范畴时，伴随的单位是一个闭嵌入.Markov的证明很复杂，随后S. Kakutani[2]、P. Samuel[3]、以及T. Nakayama[4]简化了Markov的证明，其证明方法实质上应用了现在称之为广义伴随函子定理.近年来从范畴论角度研究拓扑群范畴性质得到了广泛关注，例如拓扑群的Raǐkov完备化、拓扑群的自由积、C-紧拓扑群等.本文从3个方面介绍该领域的研究现状(自由拓扑群的内容本文暂未涉及).文中用以下符号表示相关范畴.

Set为表示集合和映射范畴;Top为拓扑空间和连续映射范畴;Gp为群与群同态范畴;TopGp2为Harsdorff拓扑群和连续群同态范畴;TopAb2为Harsdorff拓扑交换群和连续群同态范畴;TopGp为拓扑群和连续群同态范畴;TopAb为拓扑交换群和连续群同态范畴;CGp为紧拓扑群和连续群同态范畴;PCGp为准紧拓扑群和连续群同态范畴.

关于拓扑空间和拓扑群的相关概念和事实请参考文献[5-6],关于范畴论的有关概念和事实请参考文献[7-8].

1 基本性质

本节介绍拓扑群范畴的一些基本性质，包括单态射和满态射的刻画、严格单态射和严格满态射的刻画、拓扑群范畴的乘积、余积及其完备性和余完备性.

首先回顾几个范畴论的相关概念.设C是一个范畴，f:A→B是C中的态射，如果对任意2个态射g:B→C,h:B→C满足gf=hf蕴含g=h，则称f:A→B是一个满态射.对偶地如果对任意2个态射g:D→A,h:D→A满足fg=fh蕴含g=h，则称f:A→B是一个单态射.

设f:A→B是C中的单态射，并且满足对任意的分解f=ge使得e是一个满态射，则e是一个同构，称f:A→B是严格单态射.对偶地如果对f的任意分解f=mh使得m是单态射，则m是一个同构，称f:A→B是严格满态射.以下定理参见文献[9-11].

定理 1.1 范畴TopGp(TopAb)中的单态射是连续单同态；满态射是连续满同态；严格单态射是代数嵌入；严格满态射是连续商同态.

由群范畴的相关结果，该定理中关于单态射和严格单态射的证明比较简单，满态射和严格满态射的证明稍复杂.

对于Hausdorff拓扑群范畴，不能再沿用拓扑群范畴中的方法，对于Hausdorff拓扑交换群范畴有下面好的性质.

定理 1.2 范畴TopAb2中的单态射是连续单同态；满态射是连续稠密同态(即同态像在值域空间中稠密)；严格单态射是代数闭嵌入；严格满态射是连续商同态.

对于非交换的Hausdorff拓扑群范畴TopGp2，可以证明其单态射是连续的单同态，严格满态射是连续商同态.但是范畴TopGp2中的满态射是否连续稠密同态从20世纪60年代起一直是一个公开问题，直到1994年，V. V. Uspenskij[12-13]证明了该猜想是否定的.在此期间许多拓扑学家讨论了多种特殊情形，1970年,D. Poguntke[14]证明了紧拓扑群范畴中的满态射是到上的映射,特别地E. Nummela[15]证明了对于局部紧群猜想是正确的，W. F. Lamartin[16]以及P. Nickolas[17]证明了对于k群猜想是正确的.

拓扑群范畴中的乘积就是乘积拓扑群，给定一对连续群同态f:G→H与g:G→H，f与g的等值子就是拓扑子群{a∈G|f(a)=g(a)}≤G，因此下面定理是明显的.

定理 1.3 范畴TopGp(TopAb)都是良幂的、余良幂的完备范畴，遗忘函子TopGp→Top(TopAb→Top)保持极限.

对于Hausdorff群范畴有类似的结果.

定理 1.4 范畴TopGp2(TopAb2)都是良幂的、余良幂的完备范畴，遗忘函子TopGp→Top(TopAb→Top)保持极限.

拓扑群范畴的余极限远比极限复杂，由文献[18]的相关结果可知拓扑群范畴和拓扑Abel群范畴均存在余极限，并且余极限的底群恰好就是群范畴中对应图表的余极限.

定理 1.5 范畴TopGp(TopAb)存在余极限，遗忘函子TopGp→Gp(TopAb→AbGp)保持余极限.

下面考虑拓扑群范畴中的余积问题，由定理1.5，范畴TopGp(TopAb)中的余积的底群是群范畴中的余积(又称自由积).首先回顾群自由积的构造.

(x1…xn)·(y1…ym)=x1…xn·y1…ym

是一个群，称之为{Gs}i∈S的自由积，从范畴论角度就是{Gs}i∈S的余积.

定理 1.6 设{Gi}i∈I是一族拓扑群，{Gi}i∈I的余积co∏Gi存在，使得co∏Gi的底群是{Gi}i∈I的自由积，拓扑是由投射族Gi→co∏Gi,i∈I生成的最终拓扑，即使得每个投射连续的最细的拓扑.

但是很难给出拓扑群余积的拓扑直接描述.

文献[19-21]中讨论了拓扑群余积(或称自由积)的若干性质，但是很难给出拓扑群余积的拓扑明确描述.

问题 1.7 如何给出拓扑群余积的拓扑结构的明确刻画?

对于拓扑交换群，2002年P.Nickolas在文献[22]中给出了拓扑Abel群余积拓扑的明确刻画.

Nickolas在co∏Gs上构造了如下余积拓扑：

首先对于一个给定的拓扑群G，{Un}n∈Z+是单位元eG的一个开邻域序列，如果U1⊃U2⊃…，称{Un}n∈Z+是G的一个递减序列.设是是G的一族递减序列，且满足下列条件：

(U1) eG的任意开邻域U，存在{Un}∈使得U1⊂U；

(U2) 任意{Un}∈，存在{Vn}∈使得对任意的自然数n,Vn⊂Un+1；

(U3) 任意{Un}∈，存在{Vn}∈使得得对任意的自然数⊂Un；

(U4) 任意{Un}∈，存在{Vn}∈使得得对任意的自然数⊂Un；

(U5) 任意{Un}∈以及{Vn}∈，存在{Wn}∈使得得对任意的自然数n,Wn⊂Un∩Vn,

给定一个递减序列U={Un}以及x∈G，定义：

设{Gs}i∈S是一族拓扑Abel群，co∏Gs是其自由积.对于每个s∈S，若s是Gs的一个相容的递减序列族.对任意的s，记

2 拓扑群范畴的反射子范畴

回顾反射子范畴的概念.设范畴A是C的满子范畴，如果对C中任意对象B∈obC，存在A中对象A∈obA以及C中态射r:B→A(反射态射)使得对任意的g:B→A′，其中A′∈obA，存在A中唯一的态射h:A→A′满足g=rh，即下面图表交换

则称A是C的反射子范畴.如果每个反射态射r:B→A都是满态射，则称A是C的满反射子范畴.下面定理是范畴论经典结果.

定理 2.1 设范畴A是C的满子范畴，C具有(满态射，严格单态射)分解结构.则A是C的满反射子范畴当且仅当A对乘积和严格单子对象运算封闭.

考虑到拓扑群范畴TopGp以及拓扑交换群范畴TopAb都具有(满态射，严格单态射)分解结构，有下面定理.

定理 2.2 拓扑群范畴TopGp(拓扑交换群范畴TopAb)的一个满子范畴A是TopGp(TopAb)的满反射子范畴当且仅当A对乘积和子拓扑群封闭.

由于Hausdorff性关于乘积和子拓扑群封闭，因此Hausdorff拓扑群范畴TopGp2是拓扑群范畴的满反射子范畴.由于对于拓扑群T1分离性等价于完全正则性，因此Hausdorff反射等价于T1反射等价于完全正则反射，该反射非常简单.

设G是一个拓扑群，考虑商拓扑群G/{eG}-以及同态q:G→G/{eG}-，容易验证G/{eG}-是Hausdorff拓扑群并且商同态q:G→G/{eG}-是G的Hausdorff反射.

注 2.1 如果群(G,+)同时是一个拓扑空间使得加法运算+:G×G→G连续，则称G是一个仿拓扑群.如果群(G,+)同时是一个拓扑空间使得对任意的x∈G，左平移运算λx:G→G,λx(a)=x+a,a∈G连续(任意的x∈G，右平移运算μx:G→G,μx(a)=a+x,a∈G连续)则称G是一个左半(右半)拓扑群.如果G既是左半拓扑群又是右半拓扑群，则称G是半拓扑群.由于仿拓扑群的T1分离性、Hausdorff分离性以及正则分离性互不等价，近年来许多学者研究仿拓扑群和半拓扑群的T1反射、Hausdorff反射、正则反射以及完全正则反射.

推论 2.3 准紧拓扑群范畴和紧拓扑群范畴均是拓扑群范畴的满反射子范畴.

事实上可以给出拓扑群准紧反射以及紧反射的具体构造.由于Hausdorff拓扑群范畴TopGp2是拓扑群范畴的满反射子范畴，而反射是可复合的，因此只需考虑Hausdorff群.

记Υ=∏nU(n),其中U(n)是拓扑群GLn(C)中所有行列式绝对值为1的n×n矩阵子群.由Peter-Weyl定理，对任意一个紧群K，所有的连续同态K→Υ分离K中的点(参见文献[23])，因此任意一个紧群可以代数嵌入到Υ的某个幂.

引理 2.4 设G是一个Hausdorff拓扑群，记G∧是G到Υ的所有连续群同态集合，下面命题等价:

1) (G,τ)是准紧群；

3)G上由G∧诱导的拓扑是Hausdorff的并且与原拓扑相同.

推论 2.5 准紧群范畴PCGrp是Υ在TopGrp中的满反射壳.

设G是一个拓扑群，U∈N(eG)是单位元eG的一个开邻域，若存在连续群同态f:G→Υ以及V∈N(eΥ)使得U=f-1(V)，则称U是态射开集.

记N(G)=∩{U⊂G|U是态射开集,eG∈U}.

引理 2.6N(G)是G的闭的正规子群.

在交换群情形下N(G)被称为von Neumann核.

定理 2.7qG:G→ρG是G的准紧反射.

G的准紧反射也可以换一种途径得到.记G+为群G赋予Bohr拓扑，即由所有从G到Υ的连续同态生成的拓扑，由引理2.4，G+是全有界的.容易验证恒同映射G→G+是G的全有界反射.由反射具有复合性可知复合G→G+→G+/{eG}-是G的准紧反射.

记μG=σρG是ρG的Raǐkov完备化，μ:G→μG为复合σρG·qG:G→μG.则下面结果明显.

定理 2.8μ:G→μG是G的紧反射.

3 C-紧拓扑群和c-完备同态

在满足一定条件的范畴中，人们可以完全从范畴论角度定义对象的分离性、紧性以及态射的完备性等类似于拓扑空间范畴的性质[24-25].在拓扑空间范畴中，由著名的Kuratowski-Mrowka定理，空间X是紧空间当且仅当对任意拓扑空间Z，投影X×Z→Z是闭映射.D. N. Dikranjan等[26]应用Kuratowski-Mrowka定理在Hausdorff拓扑群范畴中引入了范畴紧拓扑群(简称C-紧群)的概念.

定义 3.1 设G是一个Hausdorff拓扑群，如果对任意的Hausdorff拓扑群H，投影G×H→H将闭子群映为闭子群，则称G是一个范畴紧拓扑群(简称C-紧群).

如果一个连续群同态将定义域空间的闭子群映为值域空间的闭子群，则称该映射为c-闭同态.因此上述定义中的投影可改为是c-闭的.

紧群当然是C-紧群，反之是否每个C-紧拓扑群都是紧的?2013年，A. A. Klyachko等[27]证明了存在可数以及不可数的C-紧的离散拓扑群，从而否定回答了该问题.

C-紧群在任意连续群同态下的像是Raǐkov完备的，但反之不对，因此可以引入以下概念.

定义 3.2 设G是一个拓扑群，如果对任意的连续满同态f:G→H，H都是Raǐkov完备的(等价地对任意的连续群同态h:G→K，f(G)是K的闭子群)，则称G是h-complete群.

任意一个C-紧群是h-complete群，但反之不成立，进一步C-紧群的任意闭子群是C-紧的，有以下公开问题.

问题 3.3 如果拓扑群G的任意闭子群都是h-complete群，G是否是C-紧的?

对于交换群有以下结果.

定理 3.4 设G是一个拓扑Abel群，则以下命题等价：

1)G是h-complete群；

2)G是C-紧群；

3)G是紧群.

C-紧群的任意乘积仍是C-紧群，C-紧群对于闭子群具有遗传性，因此可以用通常的方法(类似于自由拓扑群的存在唯一性证明)证明以下结果.

定理 3.5 C-紧群范畴是拓扑群范畴的满反射子范畴.

不同于紧群有万有群Υ，C-紧群的表现更复杂，甚至存在无群的离散的C-紧群，因此不能像构造紧群反射那样构造C-紧群反射.

问题 3.6 如何给出拓扑群的C-紧群反射的明确刻画?

从映射角度，与紧空间相对应的就是完备映射.类似于Kuratowski-Mrowka定理，关于完备映射有以下经典刻画定理.

定理 3.7 设X与Y是Hausdorff空间，f:X→Y是连续映射，下面命题等价：

1)f是完备映射；

2) 对任意空间Z，乘积映射f×idZ:X×Z→Y×Z是闭映射；

3)f沿着任意连续映射g:K→Y的拉回是闭映射.

最近，W. He等[28]合作在拓扑群范畴(不假设Hausdorff性)中引入了c-proper和h-complete映射，从而将C-紧群和c-complete群的概念提升到映射角度.

设f:X→Y是一个连续映射，如果对角映射δf:X→X×YX是一个闭映射(等价地，对任意的y∈Y,纤维f-1(y)是X的Hausdorff子空间)，则f称为Hausdorff(或纤维Hausdorff).显然拓扑空间X是Hausdorff的当且仅当常值映射f:X→1是纤维Hausdorff的，其中1表示单点空间.纤维Hausdorff性是空间的Hausdorff性在映射水平上的提升.

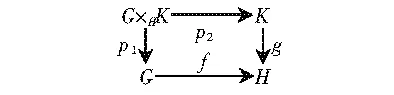
定义 3.8 设f:G→H是连续群同态.

1) 如果对任意的连续群同态g:K→H,f沿着g的拉回是c-闭的，则称f:G→H是一个c-proper同态；

2) 如果f:G→H是c-proper态射同时f是Hausdorff的，则称f:G→H是一个c-完备同态.

从以上定义容易看出，拓扑群G是C-紧的当且仅当常值映射f:G→1是c-完备的.c-proper同态和c-完备同态具有许多类似于C-紧群的性质和刻画(参看文献[28]).

定理 3.9f:G→H是连续群同态，H是Hausdorff群.则f:G→H是c-proper同态当且仅当对任意的拓扑群K，乘积映射f×idK:G×K→H×K是c-闭的.

也可以将h-complete群的概念提升到态射的水平.

定理 3.10 设f:G→H是连续群同态.

1) 如果对f:G→H的任意分解,

其中K是Hausdorff的，都有G在h下的像h(G)≤K是K的闭子群，则称f:G→H是h-complete同态.

2) 如果对f:G→H的任意分解f=k·h，其中k是Hausdorff的，都有h是c-闭的，则称f:G→H是c-complete同态.

3) 如果常值映射f:G→1是c-complete同态，则称G是一个c-complete群.

容易验证拓扑群G是h-完备的当且仅当G是Hausdorff的且常值映射f:G→1是h-完备的，任意一个c-proper同态是c-complete同态，任意一个c-complete同态是h-complete同态，任意一个c-complete同态是c-闭的，但反之不成立.

问题 3.11 h-complete同态是否一定是c-complete同态?特别地是否存在一个h-complete的Hausdorff拓扑群不是c-complete群?

问题 3.12 设f:G→H是连续群同态，满足对任意的闭子群k≤G，限制映射f|K:K→H是h-complete，f:G→H是否c-proper同态?

如果连续群同态f:G→H沿着任意连续群同态的拉回都是h-complete同态，称f:G→H是稳定h-complete同态.

问题 3.13 设f:G→H是稳定的h-complete同态，f:G→H是否c-proper同态?

对于Hausdorff拓扑交换群，C-紧群等价于紧群，也等价于h-complete群.下面是一个自然的问题.

问题 3.14 设f:G→H是连续群同态，其中G与H是Abel群.若f:G→H是c-proper同态，f:G→H是否是完备映射?进一步若f:G→H是h-complete同态，f:G→H是否是完备映射?

[1] MARKOV A A. On free topological groups[J]. C R Acad Sci URSS,1941,31:299-301.

[2] KAKUTANI S. Free topological groups and infinite discrete product topological groups[J]. Proc Imper Acad Tokyo,1944,20:595-598.

[3] SAMUAL P. On universal mappings and free topological groups[J]. Bull Am Math Soc,1948,54:591-598.

[4] NAKAYAMA T. Notes on free topological groups[J]. Proc Imper Acad Tokyo,1943,19:471-475.

[5] ARHANGEL’SKII A V, TKACHENKO M. Topological Groups and Related Structures[M]. Singapore:World Scientific,2008.

[6] ENGELKING R. General Topology[C]//Sigma Series in Pure Math, 6. Berlin:Heldermann,1989.

[7] 贺伟. 范畴论[M]. 北京：科学出版社,2006.

[8] ADAMEK J, HERRLICH H, STRECKER G E. Abstract and Concrete Categories[M]. New York:John Wiley & Sons,1990.

[9] ROELCKE W, DIEROLF S. Uniform Structures on Topological Groups and their Quotients[M]. New York:McGraw-Hill,1981.

[10] THOMAS B V S. Do epimorphisms of Hausdorff groups have dense range?[J]. Notices Am Math Soc,1970,20:A-99.

[11] THOMAS B V S. Categories of topological groups[J]. Quaestiones Math,1977,2:355-377.

[12] USPENSKII V V. The epimorphism problem for topological groups[J]. Topology Appl,1994,57:287-294.

[13] USPENSKII V V. The solution of the epimorphism problem for Hausdorff topological groups[J]. Sem Sophus Lie,1993,3:69-70.

[14] POGUNTKE D. Epimorphisms of compact groups are onto[J]. Proc Am Math Soc,1970,26:503-504.

[15] NUMMELA E. On epimorphisms of topological groups[J]. Gen Topology Appl,1978,9:155-167.

[16] LAMARTIN W F. Epics in the category ofT2k-groups need not have dense range[J]. Colloq Math,1976,36:37-41.

[17] NICKOLAS P. Free products of topological groups with a closed subgroup amalgamated[J]. J Aust Math Soc,1986,40:414-420.

[18] BROWN R, HARDY J P L. Topological groupoids I: universal constructions[J]. Math Nachr,1976,71:273-286.

[19] KATZ E, MORRIS S A. Free products of topological groups with amalgamation. II[J]. Pacific J Math,1985,120:123-130.

[20] KHAN M S, MORRIS S A. Free products of topological groups with central amalgamation I, II[J]. Trans Am Math Soc,1982,273:405-432.

[21] FAY T H. A note on Hausdorff groups[J]. Bull Aust Math Soc,1975,13:117-119.

[22] NICKOLAS P. Coproducts of abelian topological groups[J]. Topology Appl,2002,120:403-426.

[23] HEWITT E, ROSS K. Abstract Harmonic Analysis[M]. Berlin:Springer-Verlag,1963.

[24] LUDESCHER H, DE VRIES J. A sufficient condition for the existence of a G-compactification[J]. Indag Math,1980,42:263-268.

[25] THOLEN W. A categorical guide to separation, compactness and perfectness[J]. Homology, Homotopy Appl,1999,1:147-161.

[26] DIKRANJAN D N, USPENSKIJ V V. Categorically compact topological groups[J]. J Pure Appl Algebra,1998,126:149-168.

[27] KLYACHKO A A, OLSHANSKII A YU, OSIN D V. On topologizable and non-topologizable groups[J]. Topology Appl,2013,160:2104-2120.

[28] HE W, THOLEN W. Categorically Proper Homomorphisms of Topological Groups[J]. Appl Categor Struct,2016,24(5):715-732.

[29] COMFORT W W. Problems on topological groups and other homogeneous spaces[C]//van Mill J, Reed G M. Open Problems in Topology. Amsterdam:North-Holland,1990:315-347.

[30] DIEROLF S, SCHWANENGEL U. Examples of locally compact non-compact minimal topological groups[J]. Pacific J Math,1979,82:349-355.

[31] DIKRANJAN D N, GIULI E. Compactness, minimality and closedness with respect to a closure operator[C]//Mac Lane S, Adamek J. Proc Int Conf Categorical Topology, Prague. Singapore:World Scientific,1989:284-296.

[32] KATZ E, MORRIS S A. Free products of topological groups with amalgamation. I[J]. Pacific J Math,1985,119:169-180.

[33] LAMARTIN W F. On the foundations ofk-group theory[J]. Dissertationes Math,1977,146:1-32.

[34] ORDMAN E T. Free products of topological groups with equal uniformities I[J]. Colloq Math,1974,31:937-43.

[35] USPENSKIJ V V. On subgroups of minimal topological groups[J]. Topology Appl,2008,155:1580-1606.

2010 MSC：18B05; 18B10; 18D35

(编辑 周 俊)

Some Progresses on the Category of Topological Groups

HE Wei

(School of Mathematics, Nanjing Normal University, Nanjing 210097, Jiangsu)

Topological groups are important research objects in the field of topological algebras, and they are applied to many fields such as harmonic analysis, dynamic systems, etc. The category of topological groups has many interesting properties. This paper is a survey of some results on the category of topological groups. The content includes some basic categorical properties, the precompact reflections of topological groups, the compact reflections of topological groups (the Bohr compactification), Raǐkov completions, C-compact groups and c-proper homomorphisms.

topological group; continuous homomorphism; precompact group; compact group; C-compact group; c-proper homomorphism; Raǐkov completion

2016-08-30

国家自然科学基金(11571175)

贺 伟(1964—),男,教授,主要从事Locale理论、Topos理论、拓扑学(范畴拓扑、拓扑代数)、范畴论、格论、不确定性理论的研究,E-mail:weihe@njnu.edu.cn

O154.1

A

1001-8395(2016)06-0915-06

10.3969/j.issn.1001-8395.2016.06.026