机载线性调频脉冲压缩雷达杂波模型的研究
2016-05-22蔡昌勇
唐 斌, 莫 磊, 蔡昌勇, 李 莉
( 1. 电子科技大学 电子工程学院, 四川 成都 611731; 2. 成都航空职业技术学院 航空电子工程系, 四川 成都 610100; 3. 四川省高校校企联合“航空电子技术”应用技术创新基地, 四川 成都 610100)
机载线性调频脉冲压缩雷达杂波模型的研究
唐 斌1,2,3, 莫 磊2,3, 蔡昌勇2,3, 李 莉2,3
( 1. 电子科技大学 电子工程学院, 四川 成都 611731; 2. 成都航空职业技术学院 航空电子工程系, 四川 成都 610100; 3. 四川省高校校企联合“航空电子技术”应用技术创新基地, 四川 成都 610100)
与常规脉冲雷达相比,由于叠加效应,线性调频(LFM)脉冲压缩雷达的杂波信号模型有其特殊性.机载雷达与地面雷达相比,由于载机的运动会引起各个杂波单元回波多普勒频率的不同,其杂波模型更为复杂.针对LFM脉冲压缩信号及机载雷达各自的特性,提出了应用在机载雷达上的LFM脉冲压缩信号杂波模型,并对脉压前后杂波的统计特性进行仿真和分析,仿真结果表明新模型的有效性.
线性调频脉冲压缩雷达; 机载雷达; 杂波; 脉冲压缩; 统计特性
大时带积LFM信号作用距离远、距离分辨率高,与常规雷达相比,大时带积信号的杂波模型有其特殊性.文献[1-2]研究了发射信号为伪码调相连续波情况下回波信号的特点,指出各个码元回波之间会产生重叠,并对其统计性质做了分析.文献[3]论述了在低俯仰角情况下,LFM脉压回波信号展宽问题,并通过蒙特卡罗仿真给出了LFM信号下杂波模型的统计特性,但没有进行脉压后杂波模型的统计性能分析.机载雷达与一般常规地面雷达相比,杂波模型更为复杂.由于雷达载机的运动,地面杂波回波多普勒谱被大大展宽[4-5],影响了接收机的检测性能[6-8].LFM脉压信号与机载雷达各有其特点,要将二者更好的结合在一起进行取长补短,就必须结合这二者各自的特点,综合进行环境和目标特性的研究.
本文在前人研究的基础上,结合机载雷达及LFM脉压信号各自的特殊情况,提出了适用于机载雷达LFM脉压信号的杂波模型,并以蒙特卡罗方法,仿真并分析了模型的统计特性,得到了一些新的结论.
1 常规体制脉冲雷达及LFM脉压雷达的杂波模型
根据相干视频模拟原理[9-10],常规脉冲体制下,第n个随机散射体的第m个脉冲回波视频信号模型为
(1)

多个随机散射体的第m个脉冲视频回波为各个散射体回波的复数和
(2)
可以看出,假设复调制函数u(t)的脉冲宽度为T,散射体彼此之间的径向距离等于或超过cT/2时(c为光速),各个随机散射体的回波彼此不会重叠,这是常规脉冲体制下的杂波模型.
根据雷达分辨理论[11-12],雷达距离分辨率主要取决于雷达信号带宽B,距离分辨率为c/2B.常规脉冲雷达距离分辨率为cT/2,这是由于常规脉冲信号时宽和带宽有T≈1/B的关系.而LFM脉压信号的距离分辨率为cτ/2或c/2B,其中,τ=T/D,D为压缩比,T为时宽,τ为脉压后的时宽.
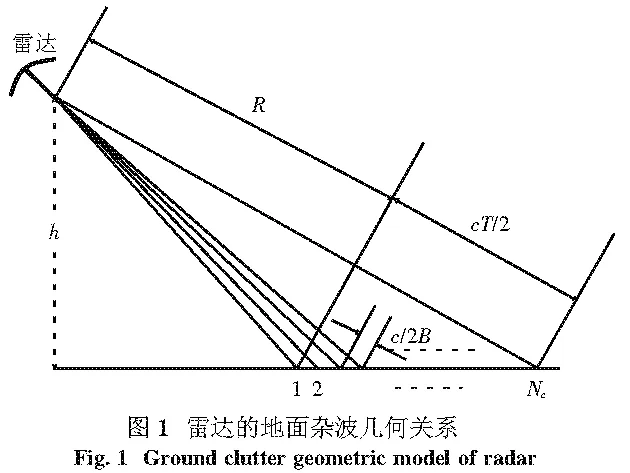
如图1所示,低仰角情况下,常规脉冲雷达的径向距离分辨单元长度为cT/2,即波束涵盖的径向长度.由于压缩比D往往很大,在常规脉冲雷达距离分辨单元内,就有Nc=TB个LFM脉压雷达的距离分辨单元.
和常规雷达的概念相对应,在整个主波束里,分成Nc个子波束,每一个子波束对应地面径向长度为c/2B的距离分辨单元.将这样的距离分辨单元映射到雷达坐标中,得到其距离门的宽度为τ=1/B.
图2表明了径向距离分辨率为c/2B的地面杂波单元回波信号与距离门之间的关系.由于每一个杂波单元的回波信号持续脉冲宽度为T,而距离门宽度为τ=1/B,在这种情况下,各个杂波单元回波信号彼此会有重叠,各个距离门回波可以看成是多个杂波单元回波的叠加,这就是LFM脉压信号体制下的杂波模型.

为了分析的方便,将整个宽度为T的LFM信号按(3)式划分为Nc个宽度为τ=1/B的子脉冲序列.
0≤t≤T.
(3)
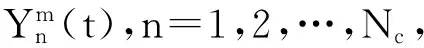
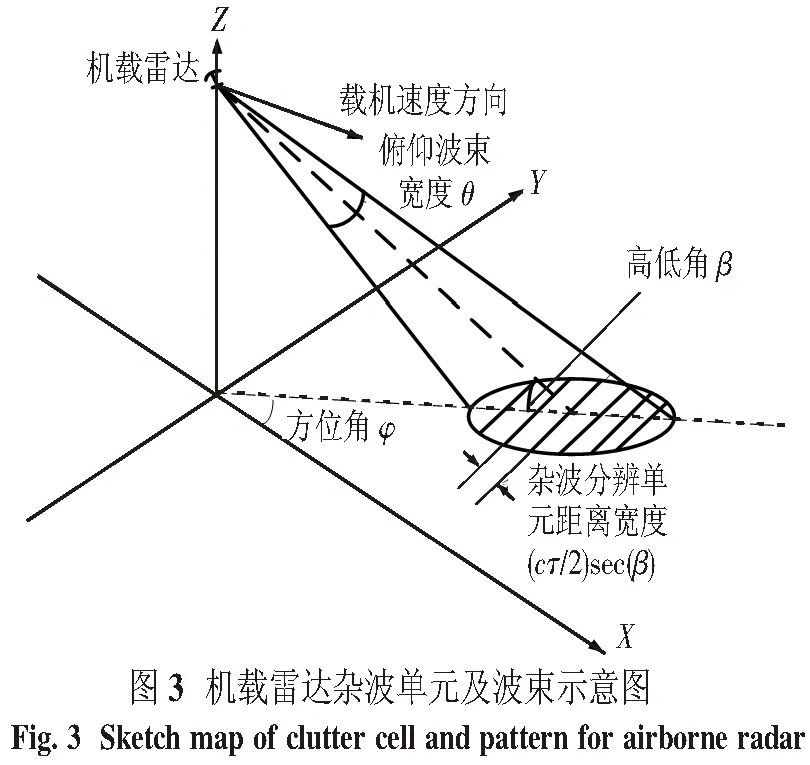
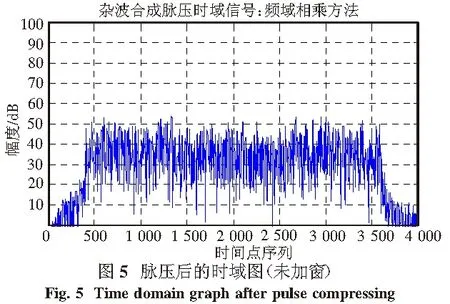
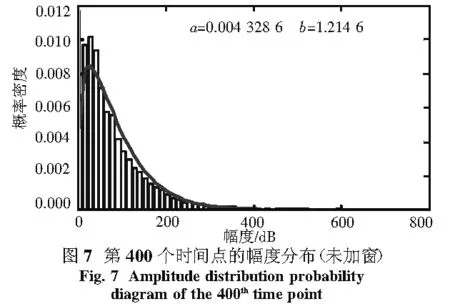
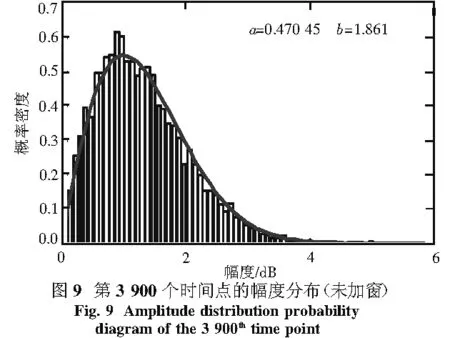
0 (4) 第k个距离门的合成回波为 (5) 将(4)式带入(5)式有 (6) 设雷达位置在载机正侧面,如图3所示,载机速度方向为X轴,大小为v,高度为H,主波束中心方位角为φ,高低角为β,主波束俯仰宽度θ,雷达波长为λ. 设初始时刻,主波束中心杂波单元的坐标为(X0,Y0,0),其与载机雷达的间距为 (7) t时刻的间距为 R2(t)=(R0cosφcosβ-vt)2+ (8) 载机与杂波单元的相对运动造成的雷达信号相位变化φ(t)可以近似地考虑为 φ(t)=2π(fdt+fdst2/2), (9) 式中 fd=2v(cosφcosβ)/λ, (10) (11) fds这个LFM项可以用已知的技术进行补偿,所以本文中将其略去.主波束中心杂波单元的多普勒频移为 fd=2v(cosφcosβ)/λ. (12) 当机载雷达为LFM雷达时,对主波束探测到的区域,按高低角的不同,杂波分辨单元按前述子波束的定义划分为条状区域,其中杂波分辨单元的长度为(cτ/2)secβ,τ为时宽(LFM信号的子脉冲宽度).由于载机的运动,不同高低角的杂波单元的多普勒频率fd不同,方位角为φ,高低角为β-θ/2+nθ/Nc的第n个杂波单元的多普勒频率为[13-14] fnd=2vcosφcos(β-θ/2+nθ/Nc)/λ. (13) 实际仿真中,都是将这些条状区域作为随机点散射体处理,将各个随机点散射体的回波信号进行合成处理.考虑到机载预警雷达的视野开阔,波束较宽、波长较短的特点,可以认为各个杂波单元的回波为独立分布的复随机信号. 根据以上的分析,第n个杂波单元回波为 (14) Kn和φn分别是杂波单元回波的随机幅度及随机相位,被认为是互相独立的随机量. 中国电波研究所对平原、丘陵和山区等典型地形进行了雷达杂波特性测试,发现韦布尔分布对实测数据的拟合较好,所以本文认为Kn是服从韦布尔分布的随机量,φn是服从(0,2π)均匀分布的随机量.根据文献[11,13-14],Kn和φn皆为慢时间变化量,在一个脉冲宽度T内Kn和φn近似保持不变.韦布尔的概率密度函数 f(x/a,b)=abxb-1e-axb,x>0. (15) 韦布尔分布所用的尺度参数a和形状参数b,由文献[15]中X波段实测数据确定为a=5,b=1. 结合(4)~(14)式,可以推出机载LFM雷达第k个距离门的合成回波为 ej4πvcos φcos(β-θ/2+nθ/Nc)t/λejφn. (16) 根据某型机载雷达的参数,假定:一个波束范围内杂波单元数目Nc=800,定义800个距离门,B=10 MHz,T=80 μs,脉冲重复频率fr=1 000 Hz,波长为0.1 m,方位角45°,高低角45°,载机速度为700 km/h,主波束俯仰宽度2°.考虑到一个子脉冲内统计性能相同,为简化起见,采样率设为10 MHz.根据(16)式,对机载LFM雷达各个距离门的合成回波做5 000次蒙特卡罗仿真试验,确定其幅度及相位分布的统计特性. 3.1 杂波幅度分布特性 对第15、60、300个距离门的合成回波幅度概率密度分布与标准韦布尔分布进行比较仿真分析,如表1所示.对合成回波仿真数据进行参数估计而得到对应的韦布尔分布的参数a、b,这里a表示尺度参数,b表示形状参数.当距离门个数变大,即叠加的杂波回波信号个数增加时,尺度参数a减小,合成杂波平均功率增大;形状参数b趋向于2,距离门的合成回波幅度趋向于瑞利分布,体现了叠加效应.值得注意的是,再将带宽降为1.25 MHz,采样率为1.25 MHz,做同样的仿真,仿真结果表明,上述规律不变,这表明对于合成回波幅度分布的“瑞利化”,带宽B起的作用很小,起主要作用的还是回波的叠加次数. 表 1 参数比较 3.2 杂波相位分布特征 根据上述理论,把(0,2π)内均匀分布的杂波相位分布与第15、60、300个距离门内相位的分布进行仿真比较.结果表明,各个距离门内的相位分布是在(0,2π)的均匀分布. 由上述合成回波幅度及相位分布可知,当多个独立杂波单元回波按(16)式进行线性叠加时,其合成杂波幅度趋向瑞利分布,相位趋向(0,2π)的均匀分布.这表明合成后杂波复信号的实部及虚部分布皆趋向于相互独立的高斯分布,同时也说明各个杂波单元回波信号对于合成杂波起的作用基本相同,并没有一个回波信号起主导作用.仿真结果还表明,随着叠加次数的增加,这样的趋势越来越明显. 3.3 脉压后的幅度分布 对于LFM脉压信号来说,了解脉压后峰值点幅度的分布更具有实际意义.对此,假定:一个波束范围内杂波单元数目Nc=800,800个距离门,B=1.25 MHz,T=80 μs,采样率5 MHz,脉冲重复频率fr=1 000 Hz,波长为0.1 m,方位角45°,高低角45°,载机速度为700 km/h,主波束俯仰宽度2°.按(16)式合成回波,再对合成回波作脉压处理,同样做5 000次蒙特卡罗仿真试验,确定其幅度、相位分布的统计特性.考虑到LFM信号对多普勒效应不敏感,所以以发射信号的共轭移位作为匹配滤波器的冲击响应. 脉压使用频域快速卷积法,即 y(n)=s(n)*h(n)= IFFT(FFT(s(n))×FFT(h(n))), (17) h(n)为发射信号的共轭移位. 图4表示脉压前的时域合成杂波幅度波形,图5表示脉压后的时域幅度波形.为了全面了解脉压对幅度的影响,主波束内第一个杂波单元回波到达接收机匹配滤波器时间设为时间轴原点,同时,为了避免和前面距离门定义相混淆,对脉压后时间位置,用时间轴数值点来表示.因此,第1个杂波单元回波信号脉压后的峰值所在坐标应为400,第800个杂波单元的回波信号的脉压峰值所在坐标应为3 600. 图6和图9分别表示脉压后时间轴上300点及3 900点上的幅度概率分布,可见,在被充分脉压前(第400个点以前及3 600点以后),前述叠加效应仍起主要作用,各个峰值点幅度分布趋向于瑞利分布.从400点开始到3 600点,由图7和图8可见,脉压效应开始起作用,脉压后峰值幅度分布与300点有显著的变化,有很明显的拖尾现象,可以用韦布尔分布近似进行定性分析.由图看出,与脉压前单个杂波单元的回波幅度分布参数(a=5,b=1)相比,脉压后尺度参数a显著减小,表明杂波平均功率大幅增加,形状参数b增加,表明幅度分布趋向于均匀,分布的方差变小.对于这个结果,我们是这样分析的:对于脉压处理前的合成回波,叠加效应起主导作用,尽管各个杂波单元的回波幅度为韦布尔分布,但其单个回波对合成回波起的作用基本相同,所以合成回波的幅度分布趋向于瑞利分布,相位趋向于(0,2π)的均匀分布.进行脉压处理后,杂波单元的回波长脉冲(T)的能量被压缩在一个短脉冲(τ)内,其峰值点是由这个杂波单元回波脉压后主瓣与相邻杂波单元回波脉压后旁瓣进行复数叠加而成,即峰值点的数值要受与其相邻杂波单元回波脉压的旁瓣影响,但相对于这个主瓣来说,旁瓣的数值相对较小,对统计性能起主要作用的还是这个杂波单元的回波信号本身的统计特性及脉压效果,所以脉压后其峰值幅度仍近似韦布尔分布,但尺度参数a减小,体现了主瓣的影响;形状参数b变大,体现了旁瓣的影响.为了与上述的叠加效应相对应,本文将这样结果称之为脉压效应. 仿真发现,加窗后的脉压幅度概率分布同样在400点与3 600点之间近似表现为韦布尔分布,其它点幅度趋向于瑞利分布.同时,尺度参数a降低得更小,形状参数b增加得更大.按照上面的分析,这是由于加窗后的主旁瓣都降低,但与主瓣相比,旁瓣降低得更多,旁瓣的影响随之减小,所以参数上表现为尺度参数a更小,表明杂波平均功率增大;主瓣变宽,使得形状参数b增大,表明幅度分布更趋向于均匀,体现了脉压效应. 仿真数据同时表明,脉压后的相位分布是在(0,2π)的均匀分布,在此由于篇幅所限,不再将图列出. 本文在前人研究的基础上,提出了机载LFM脉压雷达的杂波模型,并通过蒙特卡罗仿真试验方法,对其脉压前后不同距离门内杂波幅度及相位的统计特性进行了分析,得出了以下结论:在脉压前,距离门回波是由多个杂波单元回波线性叠加而成,随叠加次数的增加,其幅度趋向于瑞利分布,其相位趋向(0,2π)均匀分布,体现了叠加效应.在脉压后,由于脉压的作用,其幅度近似趋向于韦布尔分布,与单个杂波单元回波幅度分布(韦布尔分布,a=5,b=1)相比,脉压后峰值点幅度的参数a和b表明,平均功率增大,方差减小,大小分布更加均匀.在加窗脉压后,其幅度的分布统计性能与未加窗脉压信号稍有不同,这是脉压本身的性质形成的,体现出脉压效应.这些结论为设计机载LFM脉压雷达背景下信号检测及恒虚警处理算法提供了理论基础,具有一定的参考价值. [1] 王志华,赵兆,蔡征宇. 基于S-method的伪码调相连续波雷达调频干扰抑制[J]. 南京理工大学学报(自然科学版),2011,35(6):858-862. [2] 曹军亮,牟连云,杨网成,等. 伪码调相连续波雷达模糊函数推导及仿真分析[J]. 舰船电子对抗,2011,34(1):64-68. [3] 张长隆. 线性调频脉冲压缩雷达杂波统计模型分析[J]. 电波科学学报,2004,19(2):240-244. [4] 唐斌,曾伟一,曾友州,等. 机载相控阵雷达阵元幅相误差下的空时杂波谱[J]. 四川师范大学学报(自然科学版),2010, 33(S):476-479. [5] FERTIG L B. Analytical expressions for space-time adaptive processing (STAP) performance[J]. IEEE Transactions on Aerospace and Electronic Systems,2015, 51(1):442-453. [6] 曾伟一,唐斌,曾友州,等. 提高空时自适应处理稳健性的一种新方法[J]. 四川师范大学学报(自然科学版),2010,33(5):711-714. [7] BANG J H, MELVIN W L, LANTERMAN A D. Model-based clutter cancellation based on enhanced knowledge-aided parametric covariance estimation[J]. IEEE Transactions on Aerospace and Electronic Systems,2015,51(1):154-166. [8] EL KHATIB A, ASSALEH K, MIR H. Space-time adaptive processing using pattern classification[J]. IEEE Transactions on Signal Processing,2015,63(3):766-779. [9] MITCHELL R L. 雷达系统模拟[M]. 陈训达,译. 北京:科学出版社,1982. [10] 花汉兵. 雷达杂波模型的建立与仿真[J]. 计算机仿真,2007,24(10):92-94. [11] SKOLNI K, MERRILL I. Radar Handbook[M]. 3rd ed. New York:McGraw Hill,2008. [12] 向敬成,张明友. 雷达系统[M]. 北京:电子工业出版社,2001. [13] MAHAFZA B R. Radar Signal Analysis and Processing Using Matlab[M]. New York:Taylor & Francis Group,2009. [14] HERBERT G M. Clutter modeling for space-time adaptive processing in airborne radar[J]. IET Radar, Sonar, Navigation,2010,4(2):178-186. [15] 罗贤云,张忠治. 地物雷达杂波空间相关特性的测量与分析[J]. 电波科学学报,1995,10(3):50-56. (编辑 李德华) Research on Clutter Model for Airborne Linear Frequency Modulated Pulse Compression Radar TANG Bin1,2,3, MO Lei2,3, CAI Changyong2,3, LI Li2,3 ( 1. School of Electronic Engineering, University of Electronic Science and Technology of China, Chengdu 611731, Sichuan; 2. Department of Electronic Engineering, Chengdu Aeronautic Polytechnic, Chengdu 610100, Sichuan; 3. The Innovation Base of School-Enterprise Cooperation Aviation Electronic Technology in Sichuan, Chengdu 610100, Sichuan Compared to the traditional pulse radar, the clutter statistical model for linear frequency modulated (LFM) pulse compression radar has intrinsic special properties because of the superimposed effect. For the airborne radar, the Doppler frequency of echo signal of each clutter cell is different due to the motion of the platform. Relative to the land-based radar, the statistical clutter model of airborne radar is more complicated. In this paper, towards the characteristics of LFM signal and airborne radar, a statistical clutter model suitable for airborne radar that employs LFM waveforms is presented. The new statistical clutter model is analyzed and simulated before and after pulse compressing. The results prove the effectiveness of the proposed model. linear frequency modulated pulse compression radar; airborne radar; clutter; pulse compression; statistical characteristics 2015-04-20 国家自然科学基金(U1433129)、中国博士后科学基金(2012M511919)和四川省教育厅重点科研项目(14ZA0307) 唐 斌(1974—),男,副教授,主要从事阵列自适应信号处理、测控技术、卫星信号等技术的研究,E-mail:tbuestc@163.com TN957 A 1001-8395(2016)06-0929-06 10.3969/j.issn.1001-8395.2016.06.0282 机载雷达杂波模型

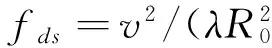
3 统计特性分析




4 结论
