自持移相LCC谐振变换器稳态分析及参数设计

高铁峰，张 森，朱 朱，赵剑锋

（东南大学 电气工程学院，江苏 南京 210096）

0 引言

LCC串并联谐振变换器兼备串联谐振、并联谐振变换器的特点，具有高功率密度、宽负载适应范围及电磁兼容特性良好等优势，在高压工业电源、通信设备、感应加热等场合得到广泛应用［1-6］。在输出侧采用单电容滤波器取代传统LC滤波器，使LCC谐振变换器的性能得到进一步提升［7-8］，但导致变换器的工作过程更加复杂。由于输出滤波器没有电感，当副边整流器导通时，两电容并联；当副边整流器关断时，两电容断开。这一过程在每个开关周期内交替出现，导致变换器具有很强的非线性特性，极大增加了电路建模、稳态分析的复杂度及控制器的设计难度。

一般采用基波近似法FHA（First Harmonic Approximation）对谐振变换器进行稳态分析，将高频变压器、副边整流器、输出滤波器及负载作为整体等效为一个电阻的形式［9］。该方法物理意义清晰、简单便捷，但无法精确描述谐振变换器的强非线性特性。文献［10］以副边整流端口为研究对象，提出了一种适用性更强的改进基波近似法，但仍用一个电阻的形式对副边进行等效，对于模型精度没有本质提升。文献［11］针对副边双路输出的串并联谐振变换器提出了一种负载线性化的分析方法，将副边等效为一个电阻和电容并联的形式，并利用傅里叶分析法将负载电流线性化处理，大幅提高了模型的精度。文献［12］分析了并联谐振电容两端电压的非线性特征，并将高频变压器、副边整流器、输出滤波器及负载等效为一个电阻和电容串联的形式，得到了更加精确的等效电路，并基于此对谐振变换器进行了稳态分析。

在谐振变换器众多控制方法中，移相控制通过改变桥臂驱动信号之间的相位角来控制输出电压，同时在稳态下保持开关频率不变，与频率控制相比具有明显的优势。但在负载变化时，为实现软开关需要调整预设开关频率，甚至在一些特定负载情况下无法实现软开关。文献［13］提出了一种混合控制方法，在负载正常情况下采用变频控制，在轻载情况下切换至移相控制，此方法弥补了2种控制方法的不足，发挥了各自的优势，但控制系统过于复杂，在实际应用中不易实施。文献［14］提出了一种谐振变换器的最优换流模式，使谐振回路输入电压和谐振电流过零点之间的相位为零，既能实现软开关又能使谐振回路的能量回流降至最低。但在负载大范围变化时仍要对频率进行较大程度的调整来满足输出电压的需求。文献［15］提出了一种谐振变换器的自持移相模式 SSPSM（Self-Sustained Phase-Shifted Mode），可以保证变换器在大范围负载变化下仍能实现软开关，同时大幅减小了开关频率的调整范围，进一步降低了损耗，提升了谐振变换器的整体效率。

本文利用改进基波近似分析法对SSPSM-LCC串并联谐振变换器进行研究，建立了等效电路并分析了谐振变换器的电压增益、谐振电流峰值、软开关区域等稳态特性。基于稳态分析提出了一种限定输入阻抗角的参数设计方法，最后搭建1.25 kW的实验平台对理论分析进行了验证。

1 LCC谐振变换器拓扑结构及SSPSM基本原理

LCC谐振变换器拓扑结构见图1。图中，VT1—VT4为开关管；Tr为高频变压器，匝比为1∶n；谐振回路由谐振电感Lr、串联谐振电容Cs和并联谐振电容Cp组成，其中Cp包含了变压器的寄生电容；VD1—VD4为整流二极管；Cf为输出滤波电容（Cf≫Cp）；RL为负载。

图1 LCC谐振变换器拓扑结构Fig.1 Topology of LCC resonant converter

分析前做如下假设：输入电压Uin恒定，由于输出滤波电容较大，可忽略输出电压Uo的高次纹波，认为其恒定；所有器件为理想器件，同时为简化分析，令变压器匝比为1∶1；开关频率大于谐振频率，因此谐振电流为正弦波；由于谐振回路的低通滤波特性，在分析时可对谐振电路输入电压UAB进行基波近似，只考虑其基波分量UAB1。

SSPSM 由 M.Youssef首次提出［16］，其主要稳态波形如图2所示。图中，Uc1、Uc2为控制电压，载波和谐振电流同步，2个控制电压分别与载波比较产生滞后桥臂和超前桥臂开关管的驱动信号；S1—S4分别为VT1—VT4的驱动信号；UAO、UBO分别为开关管VT2、VT4两端电压；α0为谐振电流过零点和开关管VT4两端电压的相位差；α为谐振电流过零点和开关管VT2两端电压的相位差。变换器处于稳态时，控制电压Uc1保持不变，从而α0不变，以此来保持开关频率恒定；Uc2为电压外环输出量，控制谐振回路输入电压UAB的下降沿滞后于谐振电流过零点角度α，既能够保证软开关的实现，又能起到调节输出电压的作用。

图2 SSPSM-LCC变换器主要波形图Fig.2 Main waveforms of SSPSM-LCC converter

SSPSM的优势在于其能够强制谐振电流滞后UAB一个相位角（如图2 所示，σ=π-α0），因此在不同负载下能够保证ZVS软开关的实现，同时以2个桥臂之间的移相角（α0-α）／2作为控制变量来控制输出电压。和传统移相模式相比，SSPSM在负载变化时能够保证软开关且减小开关频率变化范围，从而降低损耗，提高变换器效率。

如图1所示，采用单电容滤波器的LCC谐振变换器的非线性特性主要表现为：当副边二极管整流桥导通时，并联谐振电容Cp和滤波电容Cf并联，并联谐振电容电压Ucp被箝位至Uo，原边向负载传递能量；当整流桥断开时，Cp和Cf断开，谐振回路给Cp充电，原边不再为负载传递能量，负载电压由滤波电容提供，在一个开关周期内上述过程交替进行。由于副边整流桥输出电流断续且变压器两端电压和电流存在相位差，采用传统基波分析法对变换器进行分析时模型精确度较低。因此，本文将利用改进基波近似法对SSPSM-LCC变换器进行分析。

2 稳态分析及参数设计

2.1 等效电路模型

如前文所述，UAB基波分量UAB1和谐振电流ir为正弦波，表达式为：

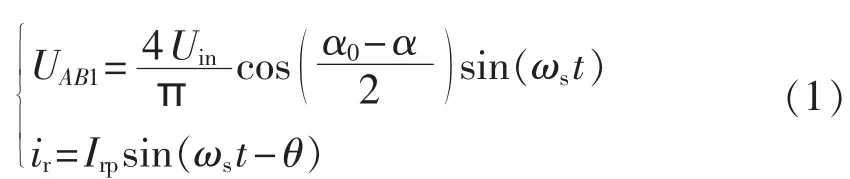
其中，Irp为谐振电流峰值；ωs=2πfs为开关角频率；θ为ir与UAB1的相位差。由图2可知，谐振电流ir过零后方向反转，开始为Cp充电（以ir正向为例），在此阶段内整流桥关断，电流iR为0。当Ucp=Uo时被箝位，整流桥导通。Cp充电时间对应的角度为φ，也可将其定义为整流桥关断角。在此阶段中Ucp可表示为：

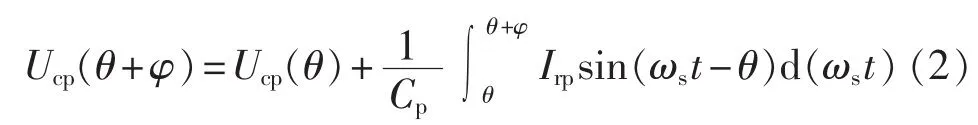
其中，Ucp（θ）=-Uo。 当 ωst=θ+φ 时，Ucp被充电至 Uo，代入式（2）可以得到关断角为：

至此，可以得到Ucp在一个开关周期内的表达式：

利用基波分量的傅里叶级数形式对Ucp和ir进行近似可以得到：

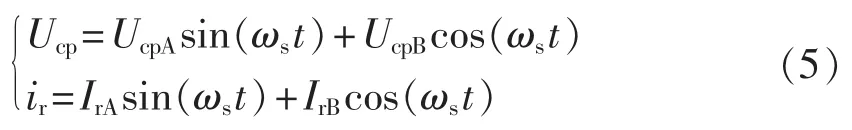
由式（4）可以计算得到Ucp的一次傅里叶系数为：

等效复数阻抗可以表示为：

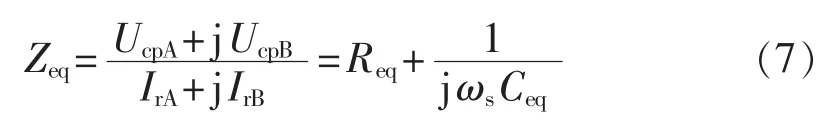
由式（5）—（7）可以得到：

由式（1）、（8）可以得到谐振回路的等效电路。稳态情况下输出电流Io等于整流桥电流在一个周期内的平均值：

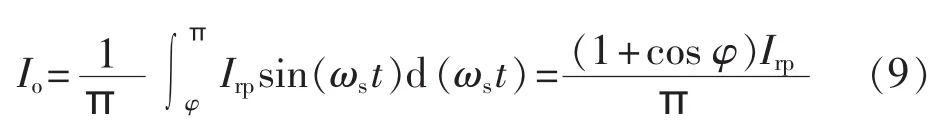
进而能够得到输出电压Uo的表达式：

根据式（1）、（8）—（10）可得到 SSPSM-LCC 变换器的等效电路，如图3所示。

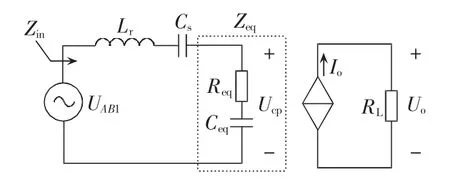
图3 SSPSM-LCC变换器等效电路Fig.3 Equivalent circuit of SSPSM-LCC converter

由图3可知，采用改进基波近似法较传统方法而言能够更加准确地描述单独滤波电容导致的强非线性特性，同时得到的等效谐振回路是一个LC串联谐振回路，且由式（8）可知等效复数阻抗求解公式简单，便于在此基础上对LCC谐振变换器进行稳态分析及参数设计。

2.2 电压增益

由式（1），UAB1表达式可以改写为：

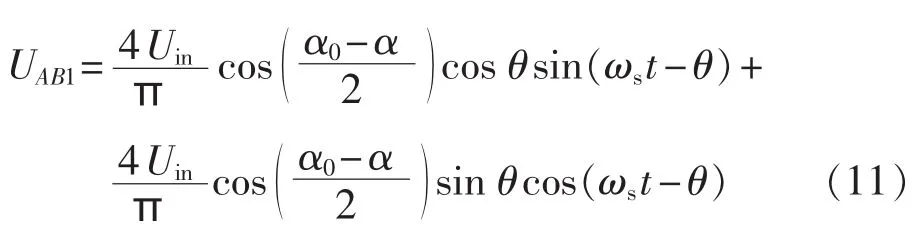
式（11）可以理解为UAB1由2个正弦电压叠加而成。其中，等式右侧第一项所描述的正弦电压和谐振电流同相位，定义为UAB1_inphase，其峰值为：

其中，θ为谐振电流和UAB1的相位差，如图2所示。θ具有重要意义：θ的取值对谐振变换器的有功功率传输起到决定性作用；θ是图3中等效电路的总输入阻抗角，与副边整流关断角φ通过等效阻抗Zeq建立起一一对应的关系；θ反映了谐振回路的感性程度，是判断软开关实现与否的标准之一。所以本文以输入阻抗角θ和整流关断角φ为主要研究对象，分析SSPSM-LCC变换器的稳态特性，为主电路参数设计及控制器设计提供理论依据。

由式（3）、（9）可以得到φ的另一种表达式：

由式（8）、（13）可以得到 Req和RL之间的关系：

根据图3所示等效电路，谐振电流峰值Irp可表示为：

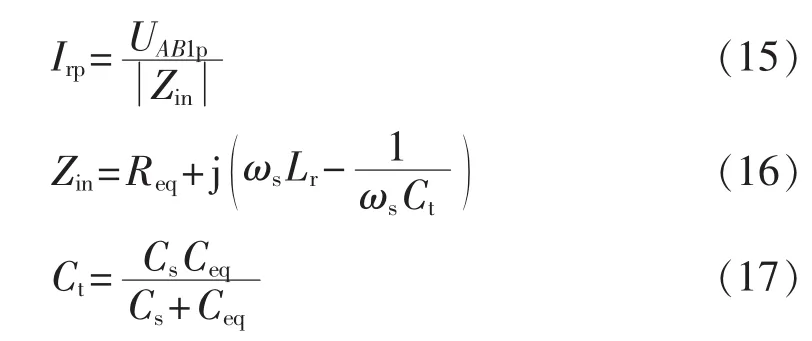
其中，UAB1p为UAB基波分量幅值；Zin为等效电路总输入阻抗；Ct为串联谐振电容Cs和等效电容Ceq串联后的电容。

定义等效电路的谐振频率ω0、归一化开关频率ωn、负载品质因数Q以及特征阻抗Z0如下：

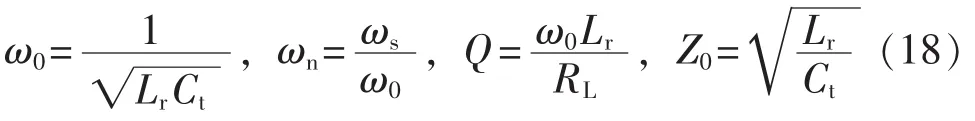
由式（1）、（15）—（18），可以得到谐振电流峰值：

将式（14）、（19）代入式（10），可以得到 SSPSMLCC变换器的电压增益：

由式（13）、（18）、（20）可以得到一组电压增益 M的曲线，如图4所示（图中ωn为标幺值，后同）。图4（a）描述了不同负载情况下的电压增益曲线，由于式（18）中的归一化参数定义考虑了负载对谐振频率的影响，所以不同负载时的电压增益都在ωn=1处取得最大值。重载时增益曲线变化率更大，当开关频率偏离谐振频率时，更快进入降压模式，变换器特性更接近于串联谐振变换器；在轻载情况下，变换器在较大频率范围内具有升压特性。图4（b）所示为整流关断角取值不同时的电压增益曲线，负载不变时整流关断角越大则电压增益越大，且当关断角大于90°时电压增益显著增加。其主要原因在于关断角度越大，时间越长，并联谐振电容Cp被充电所获得的电压也越高。因此增加整流关断角是提高变换器输出电压的有效方法之一。图4（c）反映了控制角α对电压增益的影响，从图中可以看出SSPSM-LCC变换器可以通过控制桥臂之间的移相角来控制输出电压，且电压增益和移相角成正比。为了满足自持移相条件，控制角的范围为 90°<α<α0［16］。 图4（d）比较了不同谐振电容比（A=Cp／Cs）情况下的电压增益曲线。由该曲线可以得到以下结论：电容比越大，即并联谐振电容越大，则电压增益越大；当Cp较大时，电压增益变化率较大，曲线更陡。在一些对输入或输出电压范围有特定要求的应用场合，较大的Cp值既能够满足电压增益的要求又能在几乎不提高开关频率的情况下实现软开关。但增大并联谐振电容值会导致谐振电流增加，造成更多的导通损耗，使变换器整体效率降低，因此在实际应用中应综合多方面因素折中取值。

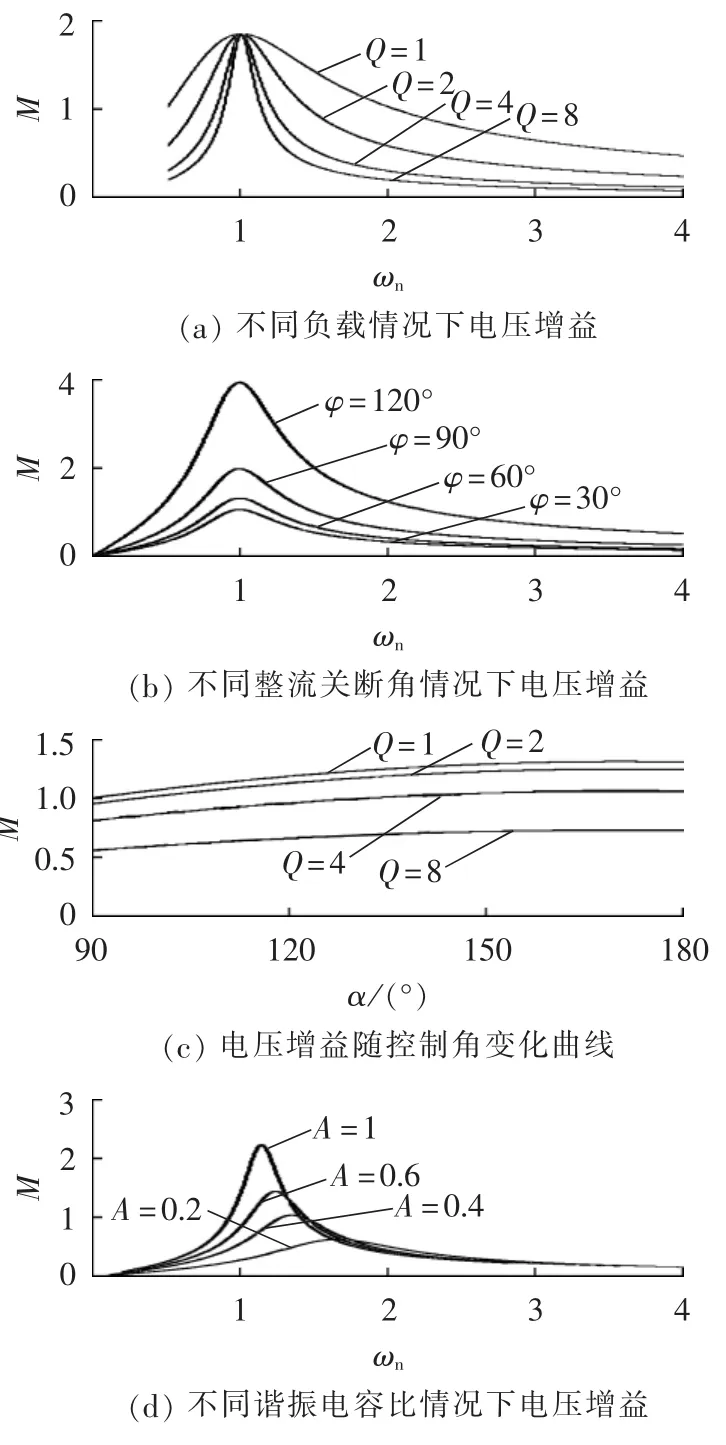
图4 SSPSM-LCC变换器稳态电压增益曲线Fig.4 Steady-state voltage gain curves of SSPSM-LCC converter

2.3 输入阻抗角与整流关断角

根据等效电路输入阻抗公式（16）可以得到阻抗角表达式为：

将式（8）、（17）、（18）代入式（21）可以得到阻抗角和关断角的关系表达式：

由式（22）能够绘制出输入阻抗角和整流关断角的关系曲线，见图5（a）。 将式（13）代入式（22）可以得到在不同负载、不同谐振电容比情况下输入阻抗角的特性曲线，分别如图5（b）、（c）所示。

图5 SSPSM-LCC变换器稳态阻抗角特性曲线Fig.5 Steady-state impedance angle curves of SSPSM-LCC converter

如图5（a）所示，输入阻抗角和整流关断角呈反比例关系。在实际参数设计中，总是希望输入阻抗角尽量大，使谐振回路在不同负载下呈感性，进而保证软开关的实现。而较大的整流关断角能够实现较大的电压增益，因此在设计取值时要综合考虑二者对变换器电压增益和效率的影响。另外，较大的谐振电容比取值能够同时扩大2个角度的选取范围，使变换器的参数设计更具灵活性。

图5（b）、（c）描述了不同电路参数条件下为了达到特定输入阻抗角所需的最小开关频率，以此可以得到实现软开关所需的最小开关频率，从而避免开关频率提升造成附加的开关损耗。通过比较能够发现，当输入阻抗角被设置某一特定值时，负载越轻或谐振电容比取值越大，则所需的开关频率越高。结合上一节对电压增益的分析，在参数设计时应综合考虑谐振电容比对电压增益、软开关实现及变换器损耗的影响。同时尽量避免或减少变换器工作在轻载下的时间。

2.4 谐振电流峰值

变换器输入有功功率为：

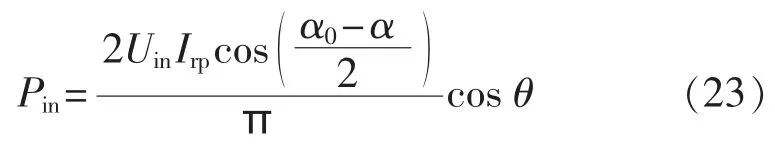
输出有功功率为：

假设 Pin=Pout，结合式（10）、（13）可以得到谐振电流峰值的表达式：

将归一化参数（式（18））代入式（25）能够得到归一化谐振电流Irp_n为：

从图2可得输入阻抗角和控制角满足如下关系：

通过式（26）、（27）可以得到不同情况下归一化谐振电流峰值曲线，如图6所示（图中Irp_n为标幺值）。

图6 归一化谐振电流峰值曲线Fig.6 Normalized peak resonant current curves

从图中可以看出，归一化谐振电流峰值随控制角增大而增加，尤其当负载较重或谐振电容比取值较大时谐振电流峰值显著增加。结合前文的分析，能够得出以下结论：控制角或谐振电容比取值较大时能够获得较大的电压增益，但会导致输入阻抗角变小，即减小了开关管的软开关范围；同时会使谐振电流峰值显著增加，增加了器件应力和导通损耗，限制了谐振变换器效率的提高。LCC变换器工作在SSPSM下较容易实现软开关，此时由谐振电流增加造成的附加导通损耗在总损耗中占据主导地位，因此在设计时应考虑参数对谐振电流峰值的影响。

2.5 软开关特性分析

实现大范围软开关是提高谐振变换器效率最有效的方法之一。对于传统移相控制，为实现大范围软开关，不仅要满足开关频率大于谐振频率，同时要保证谐振电流过零点滞后于谐振回路输入电压UAB。当负载变化时，为了满足特定的输入、输出需求，移相角需要相应改变，因此导致UAB的占空比发生变化，很难满足其与谐振电流过零点之间的相位约束条件。而对于SSPSM，可以通过控制α0来保证UAB和谐振电流过零点的相位差σ＞0（σ=π-α0，如图2所示），从而确保开关管能够实现大范围软开关。

为了进一步分析SSPSM相比于传统移相控制在软开关方面的优越性，将二者在不同负载下为实现软开关所需的最小开关频率进行对比。传统移相控制的主要稳态波形如图7所示。

图7 传统移相控制主要波形图Fig.7 Main waveforms of conventional phase-shifting control

图中α为移相角，其谐振电流过零点和UAB的相位差满足：

其中，θ为谐振回路输入阻抗角；θ1为UAB与其基波分量之间的相位角。

对于 SSPSM，由式（13）、（22）和（27）可以得到软开关范围曲线，结合式（28）、（29），能够得到 SSPSM和传统移相的软开关对比曲线图。

图8曲线比较了SSPSM和传统移相模式实现软开关所需的最小开关频率。轻载时，为了实现软开关所需的开关频率较大，随着负载加重，所需频率变小，直至接近谐振频率，SSPSM和传统移相具有相同的规律。但对于相同负载，两者所需的开关频率不同，在轻载情况下尤为明显，SSPSM-LCC谐振变换器实现软开关所需开关频率更小，进一步提升了变换器的效率。就SSPSM自身而言，不同的谐振电容比也对软开关区域有较大的影响，谐振电容比取值越小，则变换器的软开关范围越大，因此在电路参数设计时要综合考虑谐振电容比对电压增益、谐振电流峰值和软开关区域的影响。

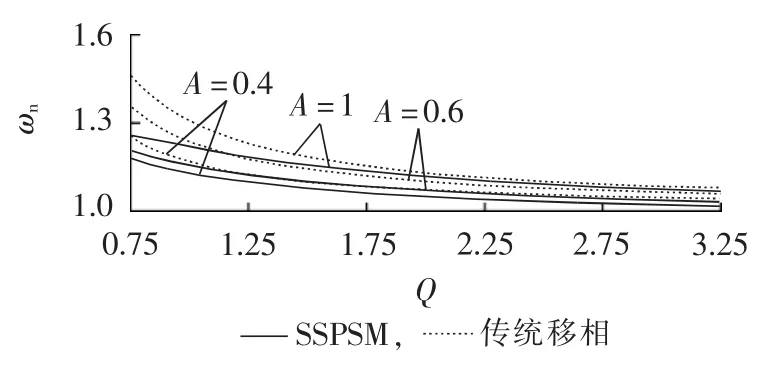
图8 SSPSM、传统移相软开关对比图Fig.8 Comparison of ZVS between SSPSM and conventional phase-shifting

2.6 参数设计

为保证变换器实现软开关，兼顾谐振电流对效率的影响，本文在参数设计时以固定输入阻抗角θ为限定条件。其他参数还包括：输入电压Uin、输出功率Po、负载电阻RL、开关频率ωs。设计过程如下。

（1）忽略所有损耗，则输入、输出功率平衡：

将式（30）、输入电压Uin和输入阻抗角θ代入式（23）可以得到谐振电流峰值Irp。

（2）通过输出电压Uo和负载电阻RL可以得到输出电流Io，将输出电流和谐振电流峰值代入式（9）能够计算得到整流关断角φ。

（3）为了减小开关损耗，设定谐振变换器工作于1.2倍谐振频率，即ωn=1.2。将ωn、整流关断角φ和输入阻抗角θ代入式（22）可以得到满足需求的谐振电容比值A。

（4） 将式（3）改写为：

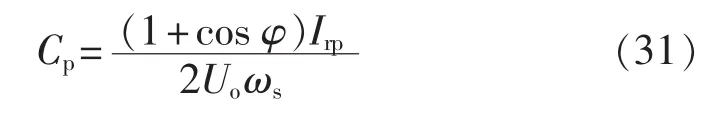
则根据已知参数及计算得到的参数可求得并联谐振电容Cp的值，然后能够得到串联谐振电容Cs：

（5）将整流关断角、并联谐振电容Cp和开关频率代入式（8）通过求解可得到等效电路的Req和Ceq。

（6） 最后将 Cs、Ceq代入式（17）、（18）可求得谐振电感Lr。

限定输入阻抗角参数设计方法的优势在于：得到的一组稳态参数能够保证谐振电流最小，从而降低了变换器的导通损耗和器件应力，在实现软开关的基础上进一步提升了变换器的效率，尤其适用于高频应用场合。

3 实验验证

为验证前文所述的理论分析，制作了一台实验样机，主要参数为：输入电压Uin=40 V，额定输出电压Uo=208 V，变压器匝比为 1∶3，谐振频率 fs=17 kHz，谐振电感 Lr=42μH，串联谐振电容 Cs=2 μF，并联谐振电容Cp=1.6μF，开关频率fr=20 kHz，额定负载RL=35 Ω。

表1比较了在不同负载情况下，直流电压增益（开环、不考虑变压器作用）与归一化谐振电流峰值的理论设计值、仿真结果及实验结果的对比。从表中可以看出，直流电压增益与归一化谐振电流值的理论设计值和仿真结果基本一致，实验结果产生的偏差主要是由各种损耗等非理想因素导致的。表1中的数据足以证明本文所述参数设计方法的正确性和有效性。

表1 SSPSM-LCC变换器稳态数据Table 1 Steady-state data of SSPSM-LCC converter

图9（a）—（c）所示分别为额定负载、50% 负载及20%负载情况下，谐振回路输入电压UAB及谐振电流ir的稳态波形。从图中可以看出，对于不同负载情况，谐振电流都滞后于谐振回路输入电压，能够说明SSPSM-LCC谐振变换器在宽范围负载变化情况下具有较好的软开关特性，同时验证了参数设计的正确性和有效性。

图9 谐振回路输入电压及谐振电流波形图Fig.9 Waveforms of resonant tank input voltage and resonant current

4 结论

本文利用改进基波近似法分析了具有电容滤波的串并联谐振变换器非线性特性，将高频变压器、副边整流器及输出滤波电容作为一个整体等效为一个复数阻抗的形式，并建立了谐振变换器的等效电路模型。在此基础上研究了电压增益、谐振电流峰值、软开关区域等稳态特性。指出了输入阻抗角、副边整流关断角和谐振电容比等关键电路参数对变换器稳态特性的影响以及设计原则，并提出一种限定输入阻抗角的参数设计方法。实验结果表明本文的分析方法能够准确地揭示谐振变换器的本质特性，参数设计方法简单有效。

［1］潘海燕，贺超，蒋友明，等.高效的LLC谐振变换器变模式控制策略［J］. 电力自动化设备，2015，35（1）：71-78.PAN Haiyan，HE Chao，JIANG Youming，et al.Efficient variant mode control of LLC resonant converter［J］.Electric Power Automation Equipment，2015，35（1）：71-78.

［2］BORAGE M，NAGESH K V，BHATIA M S，et al.Design of LCLT resonant converter including the effect of transformer winding capacitance［J］.IEEE Transactions on Industrial Electronics，2009，56（5）：1420-1427.

［3］吴建雪，许建平，陈章勇.CLL谐振变换器谐振电路参数优化设计［J］. 电力自动化设备，2015，35（1）：79-84.WU Jianxue，XU Jianping，CHEN Zhangyong.Optimal design of resonant circuit parameters for CLL resonant converter［J］.Electric Power Automation Equipment，2015，35（1）：79-84.

［4］MARTIN-RAMOS J A，PERNIA A M，DIAZ J，et al.Power supply for a high-voltage application［J］.IEEE Transactions on Power Electronics，2008，23（4）：1608-1619.

［5］夏冰，阮新波，陈武.高压大功率场合LCC谐振变换器的分析与设计［J］. 电工技术学报，2009，24（5）：60-66.XIA Bing，RUAN Xinbo，CHEN Wu.Analysisanddesignof LCC resonant converter for high voltage and high power applications［J］.Transactions of China Electrotechnical Society，2009，24（5）：60-66.

［6］CASANUEVA R，BRAÑAS C，AZCONDO F J，et al.Teaching resonant converters：properties and applications for variable loads［J］.IEEE Transactions on Industrial Electronics，2010，57（10）：3355-3363.

［7］刘和平，李金龙，苗轶如，等.无传感器混合式LLC电路同步整流数字控制策略［J］. 电力自动化设备，2015，35（1）：58-64.LIU Heping，LI Jinlong，MIAO Yiru，et al.Digital synchronous rectification control of sensorless hybrid LLC circuit［J］.Electric Power Automation Equipment，2015，35（1）：58-64.

［8］ALMARDY M S，BHAT A K S.Three-phase （LC）（L）-type series resonant converter with capacitive output filter［J］.IEEE Transactions on Power Electronics，2011，26（4）：1172-1183.

［9］ABOUSHADY A，FINNEY S，WILLIAMS B，et al.Steady state analysis of the phase-controlled LCC type series-parallel resonant converter operating above resonance［C］∥Applied Power Electronics Conference and Exposition.Long Beach，California，USA：IEEE，2013：2125-2131.

［10］IVENSKY G，BRONSHTEIN S，ABRAMOVITZ A.Approximate analysis of resonant LLC DC-DC converter［J］.IEEE Transactions on Power Electronics，2012，27（8）：3749-3763.

［11］WILLIAMS D R，BINGHAM C，STONE D A.Analysis of dualoutput resonant power converters through use of linear load approximations［J］.IEEE Transactions on Power Electronics，2012，27（9）：4051-4059.

［12］SHAFIEI N，PAHLEVANINEZHAD M，FARZANEFARD H，et al.Analysis of a fifth-order resonant converter for high-voltage DC power supplies［J］.IEEE Transactions on Power Electronics，2013，28（1）：85-100.

［13］HAYES J G，EGAN M G.A comparative study of phase-shift，frequency，and hybrid control of the series resonant converter supplying the electric vehicle inductive charging interface［C］∥Applied Power Electronics Conference and Exposition.Dallas，USA：IEEE，1999：450-457.

［14］MARTIN-RAMOS J A，SAIZ P J V，PERNIA A M，et al.Optimal control of a high-voltage power supply based on the PRCLCC topology with a capacitor as output filter［J］.IEEE Transactions on Industrial Electronics，2013，49（5）：2323-2329.

［15］YOUSSEF M Z，PINHEIRO H，JAIN P K.Self-sustained phaseshift modulated resonant converters：modeling，design，and performance［J］.IEEE Transactions on Power Electronics，2006，21（2）：401-414.

［16］SOSA J L，CASTILLA M，MIRET J，et al.Modeling and performance analysis of the DC／DC series-parallel resonant converter operating with discrete self-sustained phase-shiftmodulation technique［J］.IEEE Transactions on Industrial Electronics，2009，56（3）：697-705.