多回特高压直流分层馈入模式下交直流混联系统的稳态特性分析

赵 腾 ，张 焰 ，叶冠豪 ，张 璨 ，卫 茹 ，朱晨曦

（1.上海交通大学 电子信息与电气工程学院，上海 200240；2.国网南京市电力公司，江苏 南京 210000）

0 引言

特高压直流输电满足了在能源和负荷分布不均衡条件下进行大规模、远距离、高效率输送电力的客观需求，在中国大型能源基地的电力外送中发挥了重要作用［1-2］。随着经济的快速发展以及负荷水平的持续提高，近年来我国已有多回特高压直流线路投入运行，有效保障了负荷密集地区的能源供给。特高压直流系统的正常运行必须依托于交流电网的电压支撑，当多回特高压直流集中落点于受端系统时，不同直流系统之间的相互影响增加了系统结构及运行的复杂性，如果受端系统较弱还容易引起换相失败，限制了特高压直流的输送容量［3-4］。因此，科学评价多回特高压直流馈入下交直流混联系统的稳态特性具有重要意义。

多回特高压直流接入交流电网对于交直流混联系统的安全稳定运行提出了极大的挑战。国际大电网会议（CIGRE）在参考短路比概念的基础上，定义了多馈入短路比MISCR（Multi-Infeed Short Circuit Ratio）指标，用以评价多回直流线路馈入下交直流系统的相对强弱关系［5］。文献［6］利用MISCR对多馈入交直流系统的最大直流功率和电压稳定等问题进行了研究。文献［7］从多馈入直流系统功率稳定性角度出发，研究了多馈入直流系统功率稳定性与多馈入有效短路比之间的定量关系。文献［8-9］分析了影响MISCR的因素，有助于针对性地提高MISCR，提升交流系统对馈入直流的电压支撑作用。上述研究主要面向高压直流单层接入交流电网的场景，而文献［10］提出了一种特高压直流分层接入交流电网的方式；文献［11］进一步分析了多端单层馈入和多端分层馈入方式下直流系统的功率传输特性曲线。上述文献在受端系统对多回直流的电压支撑作用方面进行了研究，但并未涉及分层接入方式下多回直流馈入对交流系统稳态电压的影响。

本文在分析多回特高压直流不同馈入模式的基础上，考虑不同直流馈入点之间的相互影响，从MISCR、受端系统稳态电压以及直流系统极限传输功率这3个角度对多回特高压直流分层馈入模式下交直流混联系统的稳态特性进行研究，并提出了直流系统的极限传输功率分析方法，最后以两回特高压直流馈入系统为例进行仿真分析，进一步验证了理论分析的有效性。

1 多回特高压直流分层馈入模式下的系统MISCR

1.1 MISCR概念及计算

交流和直流的相互作用在很大程度上取决于交流系统与所连直流系统容量的相对大小，即短路比指标［5］。对于有单回直流接入的交直流电网，可用戴维南等值方法简化为如图1所示的形式［12］。

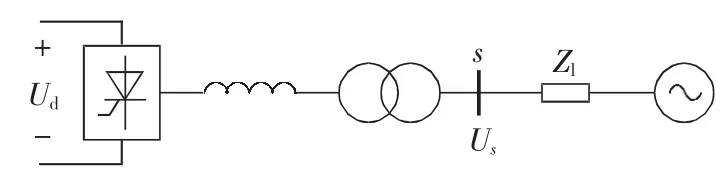
图1 单回直流馈入下的交直流系统简化模型Fig.1 Simplified model of AC-DC hybrid system with single-loop DC-infeed

图1中，Ud为直流系统电压；s为换流母线；Us为换流母线电压；Zl为交流系统等值阻抗。

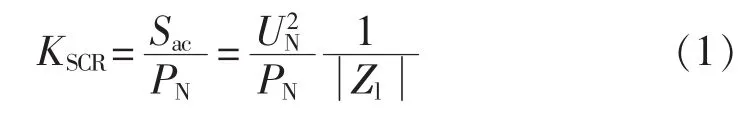
定义短路比KSCR为直流换流母线的短路容量与直流系统额定功率的比值：其中，Sac为从换流母线看出去的系统短路容量；PN为系统基准功率；UN为换流母线额定电压。

同理，通过对多端口网络进行等值化简，可将多回直流馈入下的交直流混联系统简化为如图2所示的模型［13］。

图2 多回直流馈入下的交直流系统简化模型Fig.2 Simplified model of AC-DC hybrid system with multi-loop DC-infeed

本文用i、j表示直流系统及其所包含的直流线路、换流母线的编号（i=1，2，…，n；j=1，2，…，n），则Zi表示从第i回换流母线看出去的交流系统等值阻抗；Zij表示第i回换流母线和第j回换流母线之间的等值联系阻抗。

CIGRE定义第i回直流线路的MISCR为由其换流母线看出去的交流系统三相短路容量与馈入该点的等效直流功率的比值［5］，即：

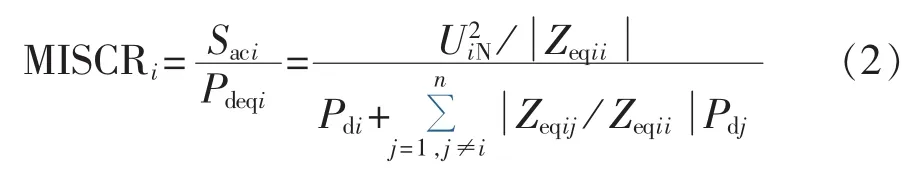
其中，MISCRi为第i回直流线路对应的MISCR；Saci为第i回直流线路换流母线对应的三相短路容量；Pdeqi为考虑了其他直流线路影响的第i回直流线路的等值输送功率；Pdi为第i回直流线路的额定功率；UiN为第i回换流母线的额定电压；Zeqij为从各换流母线看出去的等值阻抗矩阵Zeq的第i行、第j列元素；Zeqii为阻抗矩阵Zeq的第i行、第i列元素。

以UiN为基准电压，则用标幺值表示的MISCR可化简整理为：

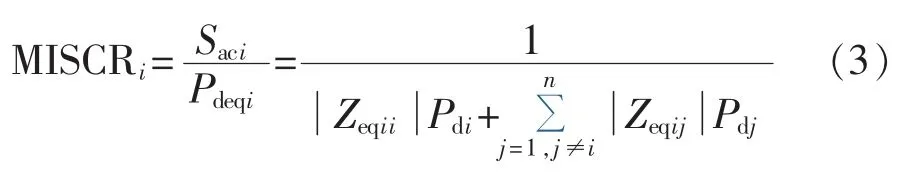
MISCR反映了多馈入交直流混联系统的电网结构强度及电网对换流母线的无功电压支撑能力的大小，因此对多馈入交直流混联系统的电压稳定具有一定表征作用，MISCR越大，表明电网对换流母线的电压支撑能力越强［6，14］。

1.2 多回特高压直流不同馈入模式下的MISCR

根据“三华”电网规划方案，未来几年华北、华中和华东地区将进一步拓展或构建500 kV和1000 kV交流主网架，所需区外来电全部通过特高压直流或特高压交流输入［1］。为了解决特高压直流馈入过程中的功率分配和转移问题，有专家提出将多回特高压直流线路采用分层方式馈入受端系统，相当于将特高压直流分为2个容量各占原直流系统一半的直流支路，分别接入不同电压等级交流电网［10，15］。 基于上述方案，本文从单层接入1000 kV电网、单层接入500kV电网以及分层接入1000kV与500kV电网这3个角度，对多回特高压直流在不同馈入模式下的MISCR进行分析。由于两回特高压直流馈入的推导相对简洁且能够直观反映MISCR的变化趋势，因此文中以两回特高压直流馈入为例进行说明。

1.2.1 两回特高压直流单层馈入模式下的MISCR

两回特高压直流单层接入1000 kV交流电网时的混联系统等值模型如图3所示。

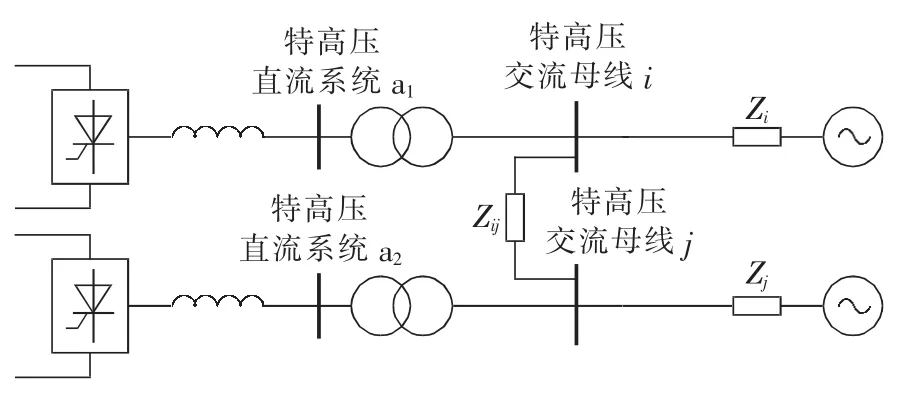
图3 两馈入特高压直流等值系统Fig.3 Equivalent system with two UHVDC infeeds

图3等值系统中的特高压交流电力网络的节点导纳矩阵Y为：

对式（4）求逆，可得节点等值阻抗矩阵Zeq为：

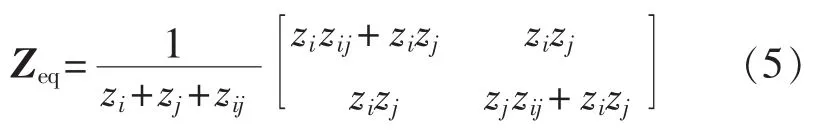
由式（5）可得式（3）中的等值阻抗为：

其中，zi和zj分别为1000 kV换流母线i和j后的系统等值阻抗；zij为换流母线i和j之间的等值联系阻抗；Zeqii和Zeqjj分别为等值阻抗矩阵中换流母线i和j对应的自阻抗；Zeqij为等值阻抗矩阵中换流母线i和j之间的互阻抗。

两回特高压直流单层接入500kV交流电网时，MISCR的计算过程与单层接入1000 kV交流电网时相同。令500 kV电网中与1 000 kV电网的zi、zj及zij相 对 应 的等值阻抗分别为 z′i、z′j和z′ij，可得在特高压直流单层接入500 kV交流电网情况下换流母线i和j的自阻抗和互阻抗为：

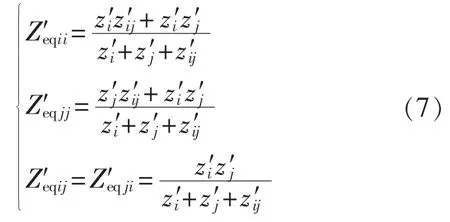
一般情况下，1000 kV网络电气联系强于500kV网络，1000 kV换流母线的短路容量比500kV换流母线的短路容量大，且其等值阻抗小，有：

其中，等值阻抗比例系数 k1、k2、k3均大于 1［10］。

（1）当时，即两回直流间的电气距离非常小，两回直流接入同一落点。根据式（6），两回特高压直流单层接入1000 kV电网时换流母线的自阻抗和互阻抗近似为：

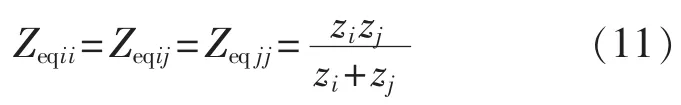
根据式（7），两回特高压直流单层接入500 kV电网时换流母线的自阻抗和互阻抗近似为：

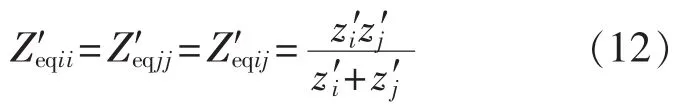
设所有阻抗角一致，则由式（8）、（9）、（11）、（12）可得：

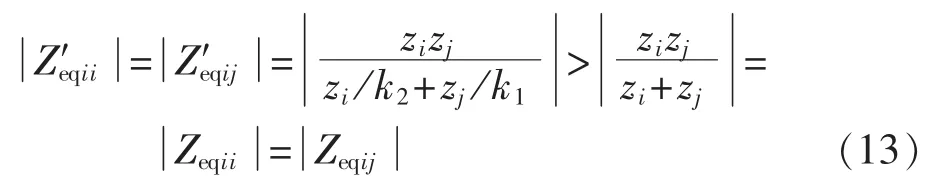
由式（3）、（13）可知，在两回特高压直流输送功率不变的情况下，单层接入500kV电网时的MISCR′i小于单层接入1000 kV电网时的MISCRi。

（2）当时，即两回直流间的电气距离无穷大，可以视为单馈入交直流系统。两回特高压直流单层接入1000 kV电网时换流母线的自阻抗和互阻抗近似为：

两回特高压直流单层接入500 kV电网时换流母线的自阻抗和互阻抗近似为：

由式（8）、（9）、（14）、（15）可得：

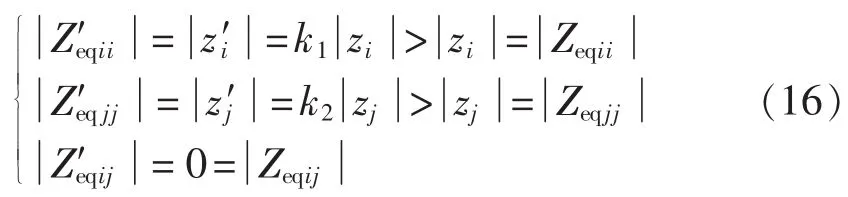
由结果可知，在两回特高压直流输送功率不变的情况下，MISCR′i＜MISCRi。

（3）当，即两回特高压直流接入不同落点时，设所有阻抗角一致，则由式（8）—（12）可得：

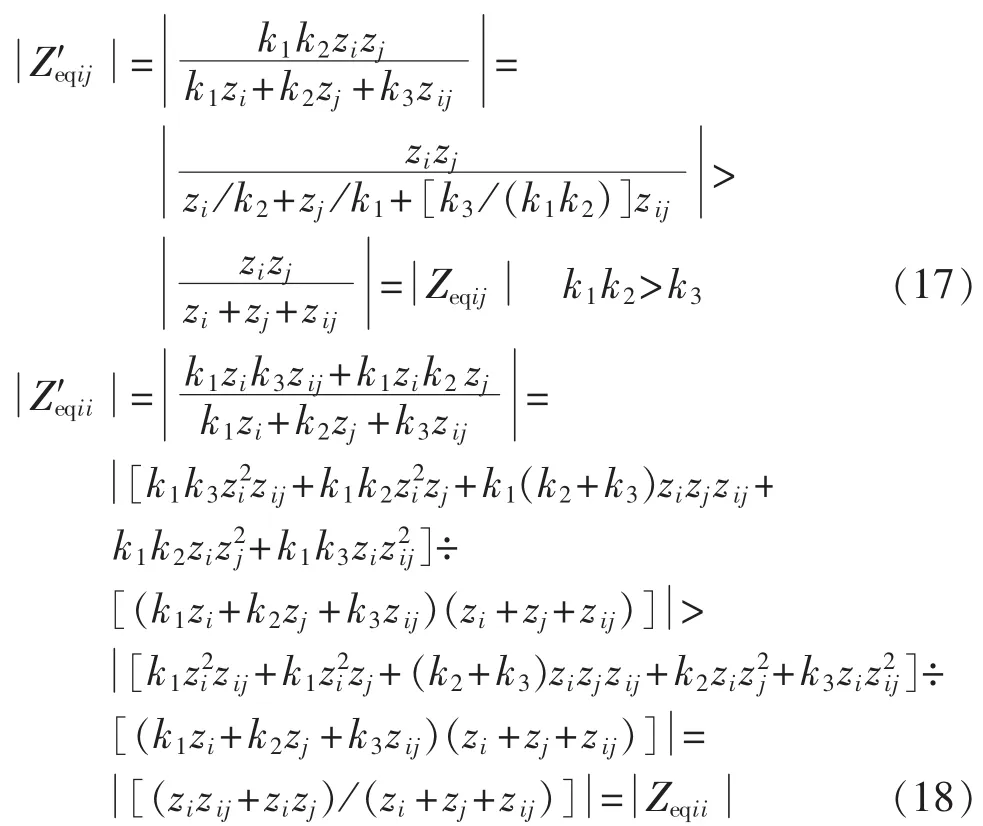
同样的，在满足k1k2＞k3且两回特高压直流输送功率不变的情况下，MISCR′i＜MISCRi。

综上所述，在一般情况下，当两回特高压直流单层馈入时，相比接入500 kV交流电网，接入1000 kV交流电网时系统具有更大的MISCR和更强的电压支撑能力。

1.2.2 两回特高压直流分层馈入模式下的MISCR

两回特高压直流分层接入1000 kV和500 kV交流电网，简化模型如图4所示。图4中，a1和a2为特高压直流系统a的2个分支，b1和b2为特高压直流系统b的2个分支。

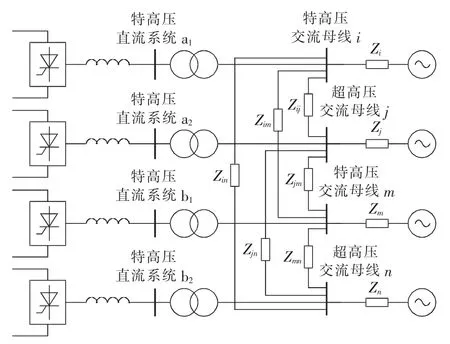
图4 两回特高压直流分层馈入简化模型Fig.4 Simplified model for hierarchical infeed of dual-loop UHVDC

假定1000 kV换流母线i和m后的系统等值阻抗值近似相等，500 kV换流母线j和n后的系统等值阻抗值近似相等，即（k＞1），且近似认为各换流母线间的联系阻抗值相同，即，则两回特高压直流分层馈入时换流母线节点所对应的导纳矩阵为：

利用MATLAB对求逆得到节点等值阻抗矩阵。在换流母线间联系阻抗相对于系统等值阻抗较小的情况下，可以忽略中各元素的余项，得到均近似为 kzi／（2+2k）。根据式（3），在两回特高压直流分层馈入模式下，第i回直流系统对应的MISCR近似为：

对比特高压直流分层接入交流电网与单层接入1000 kV交流电网这2种模式，在特高压直流落点不变的情况下，根据式（17）和（18）可得单层接入1 000 kV交流电网时系统的MISCR近似为：

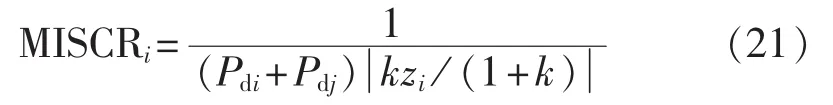
由式（20）和（21）可知，当换流母线间联系阻抗相对于系统等值阻抗较小时，两回特高压直流分层接入交流电网比单层接入1000 kV交流电网具有更大的MISCR，分层馈入模式下受端系统对直流系统具有更强的电压支撑能力。

2 多回特高压直流分层馈入模式下的交流电网稳态电压

2.1 单回特高压直流馈入时的交流电网稳态电压

在交直流混联系统中，当输电设备投切以及直流馈入功率或系统负荷发生改变时，会引起交流电网电压变化，如果受端系统较弱，交流电网的电压变化会更加明显。一般情况下，交流电网稳态电压偏离额定值越大，电网发生故障时的电压越界风险也越高。

单回直流馈入的稳态电压分析模型如图5所示。对于图5中的系统，有：

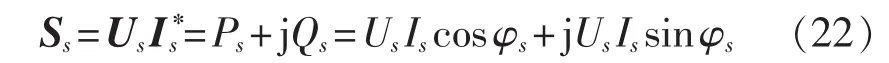
其中，Ss为换流母线s注入交流系统的单相功率；Ps和Qs分别为相应的单相有功和无功功率；Us为换流母线相电压；Is为换流母线注入交流系统的相电流；φs为功率因数角。此时对应的交流系统电压变化为：

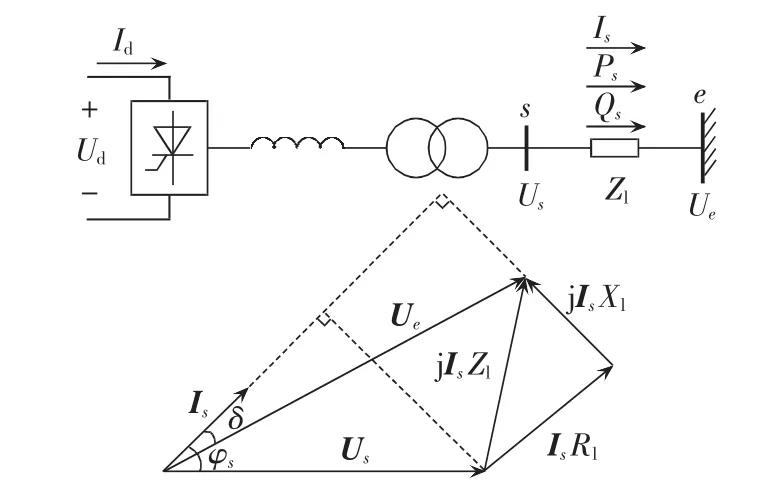
图5 单馈入直流系统稳态电压分析模型Fig.5 Steady-state voltage analysis model of single-infeed DC system

电压变化Udrop可分解为沿Is方向的IsRl以及垂直于Is方向的jIsXl2个分量（Rl和Xl分别为Zl的实部与虚部），则交流系统稳态电压Ue可表示为：

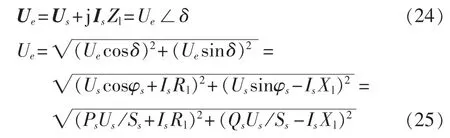
其中，δ为 Is超前 Ue的相角。 由式（22）和式（25）得：

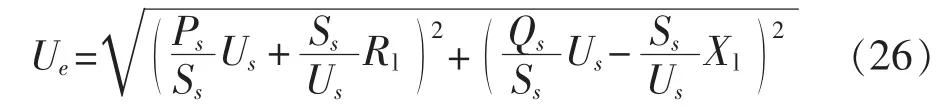
直流系统换流站运行需要大量无功功率，正常情况下约为直流传输功率的40%～60%［16-17］。此处假定Qs的大小为0.5Ps，设Us为基准电压且大小为1，代入式（26）后化简可得：

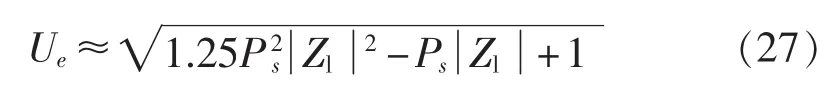
结合式（1）中的短路比定义可知，当换流母线电压固定为1时，有：

将式（28）代入式（27）得：

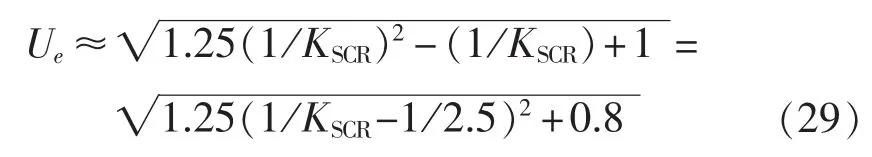
由式（29）可知，在单回直流馈入模式下，若假定换流母线相电压Us为额定值不变，有：（1）当KSCR＞2.5 时，KSCR越大，Ue越大；当 KSCR＜2.5 时，KSCR越大，Ue越小。事实上，当馈入的直流功率Ps增加时，无功消耗的增长会使得交流电压及直流电压出现不同程度的下降，即Us会降低［18］。上述分析从侧面表明，在单回直流馈入模式下，随着直流注入功率的增大，当KSCR＞2.5，即受端系统为强系统时，Ue的下降程度小于 Us；当 KSCR＜2.5，即受端系统为弱系统时，Ue的下降程度大于Us。

2.2 两回直流分层馈入时交流系统的稳态电压

当两回特高压直流分层接入交流电网时，其稳态电压分析模型如图6所示，为说明方便，图6中在考虑其他直流系统影响的条件下对单回特高压直流系统进行分析。

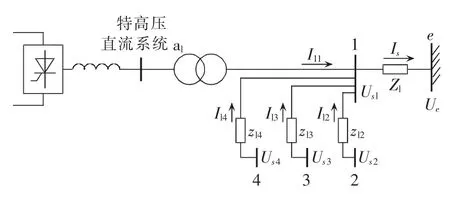
图6 特高压直流分层馈入时的稳态电压分析模型Fig.6 Steady-state voltage analysis model of UHVDC system in hierarchical infeed mode

图6中，节点1—4表示两回特高压直流分层馈入时在不同接入点的换流母线，其中节点1和3为1000 kV换流母线，节点2和4为500 kV换流母线。根据基尔霍夫电流定律，在换流母线1处注入交流电网的电流Is满足：

其中，对于电流 I1k（k=2，3，4）有：

从换流母线1处看进去的交流系统稳态电压Ue为：

将式（30）与式（31）代入式（32），得：

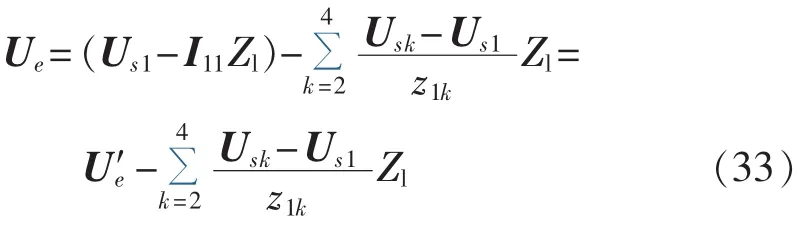
其中，U′e为不考虑其他直流系统影响时，单回特高压直流馈入情况下的交流系统稳态电压，其大小可以由式（27）计算。

当两回特高压直流单层馈入1000 kV交流系统时，对应的交流系统稳态电压为：

其中，U″e与U′e含义相同，二者的区别在于U′e计算公式中的有功功率 Ps为 U″e中的 1／2。

对比两回特高压直流分层接入交流电网与单层接入交流电网这2种模式。设ΔU为2种模式下的交流系统稳态电压差，令式（33）和（34）相减可得：

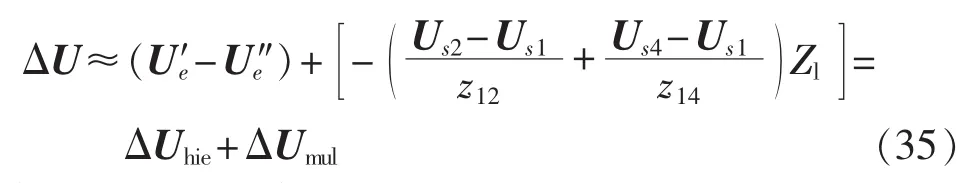
其中，ΔUhie为直流分层馈入引起的电压变化量；ΔUmul为多回直流相互作用引起的电压变化量。

令Ps为分层馈入模式下换流母线注入交流系统的单相有功功率，以Ps为变量将进行二阶泰勒展开得：

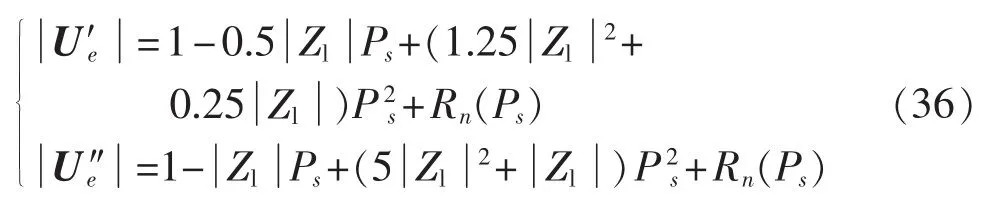
其中，Rn（Ps）为泰勒公式的余项。

在忽略U′e和U″e相位差的基础上，由式（35）和式（36）可得：

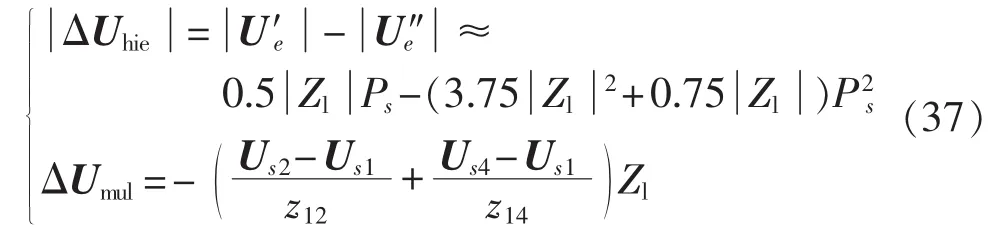
由式（37）可知，主要受直流注入功率以及馈入点的系统等值阻抗的影响；ΔUmul除了受馈入点系统等值阻抗的影响外，还与流过换流母线间等值联系阻抗的电流相关。最终决定多回特高压直流分层接入交流电网和单层接入交流电网这2种模式对交流系统稳态电压的影响，需要结合具体系统进行分析。

3 多回特高压直流分层馈入时的直流系统极限传输功率

3.1 直流极限传输功率概念

当多回特高压直流馈入交流系统时，假设所研究的第i回直流系统为定熄弧角控制，其他直流系统电流不发生变化，且保持稳定运行。第i回直流系统输送的有功功率Pi一般会随着换流母线注入交流系统电流Ii的增加而增大，在此过程中所增加的无功消耗使得交流电压及直流电压出现下降。当Ii增大到某一数值时，继续增大Ii带来的功率增长不足以抵消电压下降造成的功率下降，从而使得Pi开始降低，因此存在最大直流功率Pmax［19］。当第i回直流系统输送的有功功率Pi满足下列条件时，Pi达到最大：

随着Pi的增加，如果被馈入的交流系统支撑强度不够，则有可能在馈入的直流功率达到最大之前，交流系统已经出现潮流不收敛，从而无法继续增加直流功率至最大值。本文中将刚开始出现潮流不收敛时的直流输送功率与最大直流功率这二者的较小值定义为直流极限传输功率Plim，满足Plim≤Pmax。在多回特高压直流分层馈入模式下，由于计算第i回直流系统的Plim需要求解的稳态方程数目庞大且难以得到Plim的解析解，为此本文采用自组织临界方法，通过逐步增加直流输送功率的方式求取Plim。

3.2 直流极限传输功率计算方法

自组织临界理论是复杂科学的重要组成部分，解释了自然界中远离平衡态且彼此影响的耗散动力系统通过自组织过程向临界状态发展的过程。这类系统中能量注入是持续且缓慢的，称为慢过程；能量耗散相对而言极为迅速，称为快过程。自组织临界慢过程可以模拟电网状态缓慢发展的过程，包括发电机出力和负荷量的缓慢增加以及各支路传输容量的逐渐变化等［20-21］。为求出直流系统的极限传输功率，同时得出直流系统电流与输送功率的对应关系，本文应用自组织临界慢过程分析方法，通过缓慢增加直流系统馈入电流的方式，对直流输送功率随电流增加而变化的整体趋势进行仿真。直流系统电流的增长模型如下：

其中，I0为较小的直流系统电流初值；λi为直流系统电流增长系数。每增加一定比例的直流系统电流，即进行潮流仿真并计算直流馈入功率，直至直流馈入功率达到最大值或潮流不收敛。

4 算例分析

本文以中国某区域规划电网为例进行分析计算。该电网为包含特高压的交直流混联电网，有10个1000kV节点和10条1000 kV交流支路，并有2回特高压直流馈入。将该电网进行等值简化后其中包含220 kV及以上电压等级的节点1604个、支路2812条，总负荷2.05×105MW。在MATLAB环境下，利用 PSAT（Power System Analysis Toolbox）软件平台进行数学建模，对多回特高压直流分层馈入模式下交直流混联系统的稳态特性进行仿真分析。

4.1 特高压直流不同馈入模式下的MISCR

根据上述MISCR计算方法，分别计算两回特高压直流在单层接入500 kV交流电网、单层接入1 000 kV交流电网以及分层接入500 kV和1000 kV交流电网这3种模式下的MISCR，结果如表1和表2所示，表中各参数均以标幺值表示。

由表1可知在单层接入模式下，等值阻抗比例系数为 k1=0.65 ／0.48=1.35，k2=0.62 ／0.49=1.27，k3=0.073 ／0.051=1.43，显然 k1k2=1.71＞1.43=k3，此时两回特高压直流单层接入1000 kV电网的MISCR分别为3.071和3.172，大于单层接入500 kV电网时的MISCR，这与理论分析相符。结合表1和表2还可以看出，按照MISCR由大到小的顺序，相应的两回特高压直流馈入模式依次为：分层接入500 kV和1 000 kV交流电网，单层接入1000 kV交流电网，以及单层接入500 kV交流电网。其中，在分层馈入模式下MISCR最大。根据IEEE提出的利用MISCR划分交直流系统强弱的标准，当MISCR大于2.5时多馈入交直流系统为强系统［6］。由表1和表2中的MISCR可知，当两回特高压直流单层接入1000kV电网以及分层接入500 kV和1000 kV电网时，交流系统对馈入的直流系统具有较强的电压支撑作用。

表1 两回特高压直流单层接入交流电网时的多馈入短路比Table 1 MISCR analysis for dual-loop UHVDC in simple infeed mode

表2 两回特高压直流分层接入交流电网时的多馈入短路比Table 2 MISCR analysis for dual-loop UHVDC in hierarchical infeed mode

4.2 特高压直流不同馈入模式下的极限传输功率

从接近于0的初值开始逐步增加某特高压直流回路注入交流系统的电流，电流增长系数λ=1.01，其余直流回路的注入功率保定额定值不变。在不同馈入模式下，特高压直流传输功率随电流变化的曲线如图7所示，其中直流电流和直流馈入功率均为标幺值。

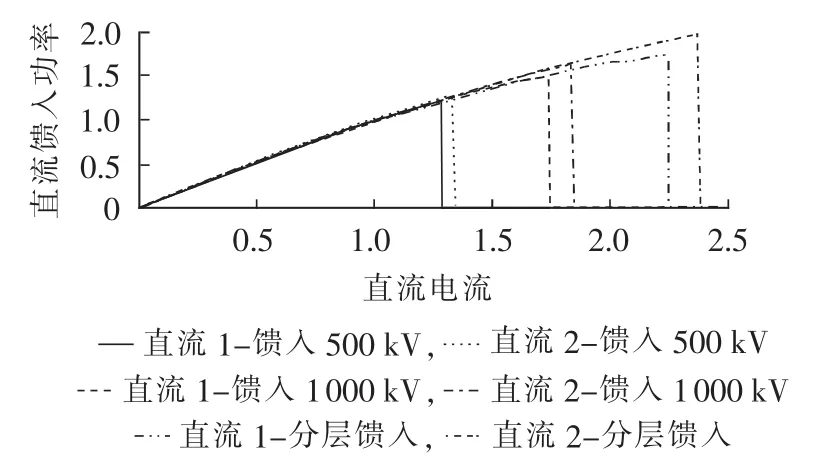
图7 特高压直流不同馈入模式下的功率曲线Fig.7 Power curve of UHVDC for different infeed modes

在3种不同的馈入模式下，交流系统均于两回特高压直流未到达最大传输功率前出现潮流不收敛。由图7可知，特高压直流接入500 kV交流电网时，两回直流的极限传输功率分别为其额定功率的1.23倍与1.25倍；接入1000 kV交流电网时，两回直流的极限传输功率分别为其额定功率的1.51倍与1.65倍；分层接入500 kV和1 000 kV交流电网时，两回直流的极限传输功率分别为其额定功率的1.74倍与1.98倍。上述结果表明在本算例中采用分层馈入模式有助于增大直流系统的极限传输功率，提高交流系统对特高压直流的电压支撑能力，增加交直流混联系统的稳定裕量。

5 结论

本文重点分析了两回特高压直流在3种馈入模式下的MISCR、交流系统稳态电压以及直流极限传输功率，结论如下。

（1）在一定条件下，当两回特高压直流馈入受端系统时，分层接入1000 kV和500 kV交流电网、单层接入1000 kV交流电网、单层接入500 kV交流电网这3种模式所对应的MISCR的数值依次降低。分层馈入模式有助于促进不同电压等级电网之间的协调配合，提高交流系统对特高压直流的电压支撑能力，提升交直流混联系统的安全性。

（2）在特高压直流单层馈入模式下，当受端系统较强时，随着直流注入功率的增大，交流系统稳态电压的降幅小于直流接入端电压；当受端系统较弱时，随着直流注入功率的增大，交流系统稳态电压的降幅大于直流接入端电压。

（3）对两回特高压直流馈入系统，在不同馈入模式下直流系统的极限传输功率随MISCR的增加而增大，二者呈正相关关系；采用分层馈入模式有助于增大直流系统的极限传输功率，提高交直流混联系统的稳定裕量。

［1］刘振亚.特高压交直流电网［M］.北京：中国电力出版社，2013：11-14，108-111.

［2］邓旭，王东举，沈扬，等.±1100 kV准东—四川特高压直流输电工程主回路参数设计［J］. 电力自动化设备，2014，34（4）：133-140.DENG Xu，WANG Dongju，SHEN Yang，etal.Main circuit parameter design of Zhundong-Sichuan±1100 kV UHVDC power transmission project［J］.Electric Power Automation Equipment，2014，34（4）：133-140.

［3］KRISHAYYA P C S，ADAPA R，HOLM M，et al.IEEE guide for planning DC links terminating at AC locations having low short-circuit capacities，part I：AC ／DC system interaction phenomena［R］.Paris，France：CIGRE，1997.

［4］袁阳，卫志农，雷霄，等.直流输电系统换相失败研究综述［J］.电力自动化设备，2013，33（11）：140-147.YUAN Yang，WEI Zhinong，LEI Xiao，et al.Survey of commutation failures in DC transmission systems［J］.Electric Power Automation Equipment，2013，33（11）：140-147.

［5］CIGRE Working Group B4.41.Systems with multiple DC infeed［R］.Paris，France：CIGRE，2008.

［6］林伟芳，汤涌，卜广全.多馈入交直流系统短路比的定义和应用［J］. 中国电机工程学报，2008，28（31）：1-8.LIN Weifang，TANG Yong，BU Guangquan.Definition and application ofshortcircuitratio formulti-infeed AC／DC power systems［J］.Proceedings of the CSEE，2008，28（31）：1-8.

［7］黄弘扬，徐政，许烽.多馈入直流输电系统短路比指标的有效性分析［J］. 电力自动化设备，2012，32（11）：46-50.HUANG Hongyang，XU Zheng，XU Feng.Effectiveness of short circuit ratio index for multi-infeed HVDC system ［J］.Electric Power Automation Equipment，2012，32（11）：46-50.

［8］林伟芳，汤涌，郭小江.多馈入交直流系统短路比影响因素分析［J］. 电网技术，2011，35（8）：64-68.LIN Weifang，TANG Yong，GUO Xiaojiang.Analysis of influencing factorsofshortcircuitratio ofmulti-infeed AC／DC power systems［J］.Power System Technology，2011，35（8）：64-68.

［9］郭小江，汤涌，郭强，等.CIGRE多馈入直流短路比指标影响因素及机理［J］. 电力系统保护与控制，2012，40（9）：69-74，81.GUO Xiaojiang，TANG Yong，GUO Qiang，et al.Influence factors and theory for CIGRE MISCR index［J］.Power System Protection and Control，2012，40（9）：69-74，81.

［10］刘振亚，秦晓辉，赵良，等.特高压直流分层接入方式在多馈入直流电网的应用研究［J］. 中国电机工程学报，2013，33（10）：1-7.LIU Zhenya，QIN Xiaohui，ZHAO Liang，et al.Study on the application of UHVDC hierarchical connection mode to multiinfeed HVDC system［J］.Proceedings of the CSEE，2013，33（10）：1-7.

［11］高媛，韩民晓.特高压直流输电多端馈入方式稳态特性研究［J］.电网技术，2014，38（12）：3447-3452.GAO Yuan，HAN Minxiao.Steady state characteristic of multi infeed UHVDC power transmission［J］.Power System Technology，2014，38（12）：3447-3452.

［12］DE TOLEDO PF，BERGDAHLB，ASPLUND G.Multiple infeed short circuit ratio-aspects related to multiple HVDC into one AC network［C］∥Transmission and Distribution Conference and Exhibition：Asia and Pacific.Dalian，China：IEEE，2005：1-6.

［13］徐箭，张华坤，孙涛，等.多馈入直流系统的特高压直流接入方式优选方法［J］. 电力自动化设备，2015，35（6）：58-63.XU Jian，ZHANG Huakun，SUN Tao，et al.Optimal selection of UHVDC connection mode to multi-infeed HVDC system ［J］.Electric Power Automation Equipment，2015，35（6）：58-63.

［14］林伟芳，汤涌，卜广全.多馈入交直流系统电压稳定性研究［J］.电网技术，2008，32（11）：7-12.LIN Weifang，TANG Yong，BU Guangquan.Study on voltage stability of multi-infeed HVDC power transmission system［J］.Power System Technology，2008，32（11）：7-12.

［15］李传栋，杨桂钟，陈晶腾，等.特高压直流分层接入方式的落点选择研究［J］. 福建工程学院学报，2014，12（6）：567-572.LI Chuandong，YANG Guizhong，CHEN Jingteng，et al.Study on DC linkstermination selection ofUHVDC hierarchical connection mode［J］.Journal of Fujian University of Technology，2014，12（6）：567-572.

［16］刘晓明，慈文斌，刘玉田.直流控制方式对受端电网电压稳定性影响［J］. 电力自动化设备，2011，31（4）：69-73.LIU Xiaoming，CI Wenbin，LIU Yutian.Influence of DC system control mode on voltage stability of receiving-end power grid［J］.Electric Power Automation Equipment，2011，31（4）：69-73.

［17］徐梅梅，李兴源，白加林，等.交直流并联系统的换流母线电压稳定性分析［J］. 电力系统自动化，2009，33（7）：6-10.XU Meimei，LI Xingyuan，BAI Jialin，et al.Analysis on voltage stability atcommutation buses ofparallelAC／DC power systems［J］.Automation of Electric Power Systems，2009，33（7）：6-10.

［18］张建设，张尧，张志朝，等.交直流并联系统的电压稳定研究综述［J］. 继电器，2005，33（2）：79-84.ZHANG Jianshe，ZHANG Yao，ZHANG Zhichao，et al.Voltage stability study of parallel AC ／DC power systems［J］.Relay，2005，33（2）：79-84.

［19］AIK D L H，ANDERSSON G.Power stability analysis of multiinfeed HVDC systems［J］.IEEE Transactions on Power Delivery，1998，13（3）：923-931.

［20］易俊，周孝信，肖逾男.电力系统自组织临界特性分析与仿真模型［J］. 电网技术，2008，32（3）：7-12.YIJun，ZHOU Xiaoxin，XIAO Yunan.Analysis on power system self-organized criticality and its simulation model［J］.Power System Technology，2008，32（3）：7-12.

［21］曹一家，曹丽华，李勇，等.考虑大停电风险的多阶段电网扩展规划方法［J］. 电力自动化设备，2014，34（6）：1-7.CAO Yijia，CAO Lihua，LI Yong，et al.Multi-stage transmission expansion planning with consideration of large-area outage risk［J］.Electric Power Automation Equipment，2014，34（6）：1-7.