计及源荷双侧响应的概率潮流计算方法

周 竞，王 珂，石 飞，冯树海

（中国电力科学研究院，江苏 南京 210003）

0 引言

近年来，以风电为代表的大规模间歇性能源的渗透率迅猛增长，其出力不确定性将大幅增加电力系统供需的波动性，系统频率稳定及电网安全将面临新的挑战［1-5］。

随着智能电网发展的进一步推进，源荷双侧协同调度将成为平衡新能源波动的有效手段之一。文献［6］提出了源荷双侧灵活互动的技术内涵和研究框架；文献［7-8］建立了源荷双侧一体化调度的模型，以用电激励负荷、可中断负荷、分时电价负荷等可调度负荷资源作为常规发电的补充，有效提高了风能利用效率；文献［9-10］探索了负荷参与调度的可执行模式，包括虚拟发电机建模方式和多代理需求响应调度模型等。以上研究均验证了负荷侧资源协同发电侧资源参与系统功率平衡有利于电网安全经济运行，是未来智能电网调度的发展趋势。

为了充分考虑间歇性能源等随机因素的影响，更全面、深刻地揭示电力系统的实际运行情况，概率潮流受到越来越多的关注。概率潮流是利用概率统计方法处理电力系统运行中各种随机因素的一种有效方法［11-12］，具有代表性的分析方法有：半不变量法［13-14］、点估计法［15-16］、拉丁超立方法［17］和蒙特卡洛抽样法［18-19］。上述算法各有优劣，而基于半不变量法的概率潮流由于其计算速度快、物理概念清晰而具有较好的工程应用前景。然而，半不变量法的前提为假设输入变量相互独立，因此研究中往往隐含着系统不平衡功率由指定的一台平横机承担，忽略了常规可调机组和柔性负荷响应参与功率调节，这与实际电网运行有较大的出入［20］。当系统随机因素较多且随机波动较大时，随机潮流计算结果将产生较大的误差，导致调度人员发生误判等问题。

实际电网中，为了应对风功率的随机性，常通过常规可调度火电、水电以及柔性负荷来响应风电的随机性以实现供需的瞬时平衡。因此，系统不平衡功率与可调度资源的响应量之间有明确的关联关系。为有效地计及源荷双侧响应对潮流分布的影响，本文首先建立了系统随机注入量和响应量的概率模型，并在常规半不变量概率潮流模型的基础上，从不平衡功率基准值的分配和响应随机变量的计算2个方面对算法进行改进。最后，以实际电网为算例，验证了本文所提的计及源荷双侧响应的概率潮流算法的有效性和准确性。

1 系统随机注入量的概率模型

文献［21］用动态随机变量DRV（Dynamic Random Variable）来描述既有一定规律性又带有随机性的现象，即在各种确定性规律基础上叠加相应的随机波动性来建立随机注入量的概率模型，可表示为：

其中，W（t）为随时间 t变化的动态随机变量；W0（t）为 W（t）中按规律变化的确定性部分；Δ（t）为随机变量，用来反映W（t）中的随机波动部分。

以风电、光伏发电为代表的间歇性电源具有一定的随机性。以风电为例，风电预测精度与预测时间尺度相关，日前风电场风电的预测误差一般为25%～40%，有时可能更大；日内预测误差相对较小，但大多也在10%以上。如式（2）所示，可将风电功率分解为表征确定性的基础部分和表征随机性的不确定部分。其中，i为节点编号；PW0i为节点i所连风电场风功率的预测值；ΔPWi为预测偏差量。

风电功率预测误差的概率分布［22］可用正态分布、拉普拉斯分布、威布尔分布、分段指数分布等多种模型来表示。本文采用正态分布作为风电功率预测误差的分布模型，如式（3）所示。假设某节点i所连风电场的预测误差 xWi服从正态分布 N（0，σWi），其中方差σWi取决于预测时间尺度。

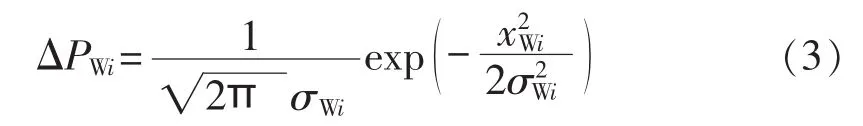
由于人类活动既具有规律性，也存在很强的随机性，电力负荷同样可用式（1）的形式表示，见式（4）。以节点i上所连负荷的预测误差xLi为例，可用正态分布具体表示，如式（5）所示。

其中，PL0i为节点i负荷的预测值；ΔPLi为该负荷的预测偏差量。目前电力负荷的短期预测精度较高，当采用正态分布模拟预测偏差时，其方差σLi一般较小。

2 源荷双侧响应量的概率模型

当大规模间歇性能源并网后，其间歇性和波动性将增大系统运行中的不平衡功率，由于间歇式发电和负荷预测的随机性，系统不平衡功率表示为：

其中，PUnb为系统不平衡功率；PUnb0为不平衡功率中的确定性部分；ΔPUnb为随机性部分。

为应对系统中的不平衡功率，传统电网中往往配备一定容量的可调机组即自动发电控制（AGC）机组参与调节，且按照一定的分配系数来承担系统总功率缺额，分配系数大小一般由可调机组的爬坡速率或剩余裕度决定。然而，负荷侧可调度资源具有响应速度快和经济性高等优势［22］，在未来智能电网下，源荷双侧共同参与调节是发展的必然趋势。本文将负荷侧可调度资源近似成负的可调发电机，共同承担系统总功率缺额，分配系数由其响应速率或响应潜力决定。系统在一定运行工况下，源荷双侧响应资源是已知的，因此其分配系数也是已知的，表征着各响应资源承担不平衡功率的比例。源荷双侧响应资源的调度量可看作由于间歇性发电和负荷波动引起的不平衡功率的响应量，表示为：

其中，KG和KFld分别为常规可调机组和柔性负荷的功率分配系数；dPGr为常规可调节机组响应不平衡功率的调节量，包含确定性部分KGPUnb0和随机性部分KGΔPUnb；dPFldr为柔性负荷响应不平衡功率的调节量。可见，由于间歇性电源和负荷预测的随机性，使得系统不平衡功率存在一定的随机性，因此常规机组和柔性负荷的响应调节量也存在一定的随机性。

3 概率潮流模型

3.1 常规半不变量概率潮流模型

节点功率方程可表示为：

支路潮流功率方程可表示为：

其中，j∈i表示所有和节点i相连的节点j，包括j=i；Pis、Qis分别为节点i的有功和无功注入功率，Pis=PGi+PWi-PLi，Qis=QGi+QWi-QLi；Ui、Uj分别为节点 i与 j的电压幅值；θij为节点 i与 j间的相角差；Gij、Bij分别为导纳矩阵元素Yij的实部和虚部；Pij、Qij分别为支路i-j上的有功与无功潮流；bij0为支路i-j容纳的1／2；tij为支路变比标幺值。事实上，由于风电的反调峰作用，其间歇性和波动性往往使得系统产生较大的不平衡功率，基于式（8）的概率潮流模型由平衡节点承担系统所有不平衡功率，往往导致平衡机出力偏离正常值较多并可能产生越限，从而影响计算的精度。

对式（8）和式（9）进行泰勒展开，忽略 2次及以上高次项，整理可得：

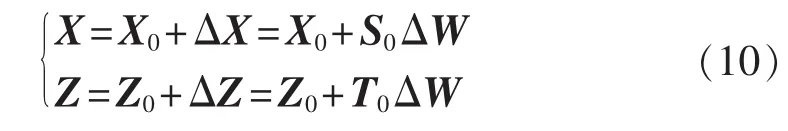
其中，X、Z分别为节点电压和支路功率，下标0表示基准运行状态；ΔW为注入功率的随机变化量；S0、T0分别为节点电压和支路功率对注入功率变化的灵敏度，为雅可比矩阵。假设所有节点注入功率的随机变化量相互独立，根据半不变量性质，节点i注入功率的k阶半不变量为：

其中，分别为节点i上风电场注入功率和负荷注入功率的k阶半不变量。输出变量的各阶半不变量可由式（12）得到：

其中，分别为矩阵S0和T0中元素的k次幂所构成的矩阵。

目前，基于半不变量计算输出变量概率分布级数的方法主要有Gram-Charlier级数、Von-Mises级数等，本文采用Gram-Charlier级数展开，这里不再赘述。

3.2 计及源荷双侧响应的概率潮流

3.2.1 不平衡功率基准值的分配

由3.1节的分析可知，间歇性电源和负荷预测的随机性使得系统不平衡功率以及常规可调机组和柔性负荷的响应调节量存在一定的随机性，假设N为系统中节点个数，PG0i为节点i上常规电源的出力基准值，Ploss为系统网损。若忽略网损的不确定性，可得到：

基于动态潮流［23］的思想，假设节点i上存在可调度的常规机组或柔性负荷，则其不平衡功率分配系数为：

其中，kGi为节点i所连机组的功率分配因子，kGi=0时表示该节点无可调度机组；kFldi为节点i柔性负荷的功率分配因子，kFldi=0时表示该节点无柔性负荷

由此可知，节点i的注入功率可表示为Pi=PG0i+PW0i-PLi-kiPUnb0，将其代入式（8）的有功潮流方程，可表示为：

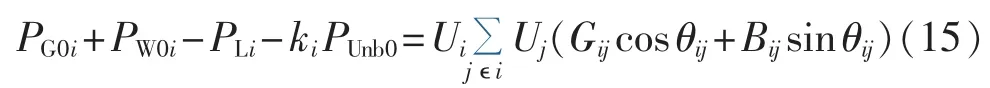
网损可表示为：

考虑网损的引入，潮流方程雅可比矩阵的修正量为：

可见，有功方程中网损Ploss的引入，将破坏原常规潮流雅可比矩阵的稀疏性。为了利用原常规潮流雅可比矩阵的稀疏性，采用直接修正有功失配量方法求解网损，即在求解动态潮流某一工作点时，在潮流迭代第g步的过程中，首先计算第g-1步的网损变化量：

以该网损变化量修正第g步系统的网损变化量，即在迭代过程中，忽略Ploss的引入对雅可比矩阵的修正量，直接使用原雅可比矩阵进行迭代求解。

3.2.2 计及源荷双侧响应的随机变量计算

由式（7）可得：

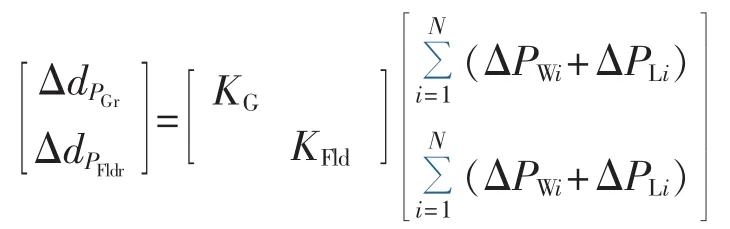
记为：

其中，ΔdPR为所有参与不平衡功率分配的机组和负荷的响应随机变量矩阵；K为分配系数矩阵；ΔWn为表征风电场和负荷随机性的变量矩阵。以式（10）第1项节点电压方程为例进行随机变量的计算，随机变量包括风电场随机性、负荷随机性以及响应不平衡功率的响应量的随机性，可表示为：

其中，E为单位矩阵。

3.2.3 求解流程

基于上述分析，计及源荷双侧响应的概率潮流仿真计算流程如图1所示。

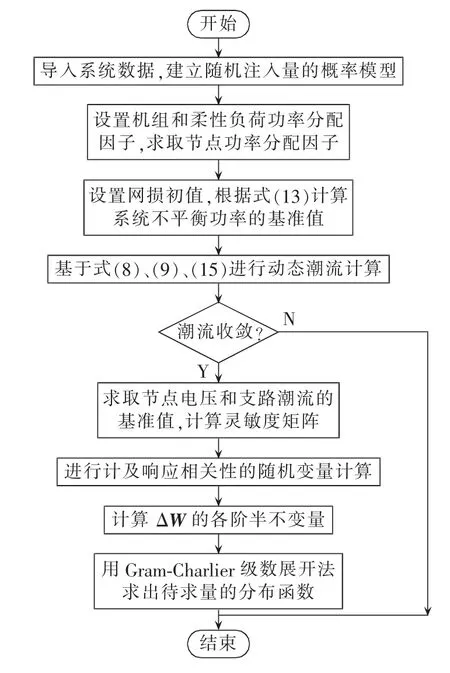
图1 计及响应相关性的概率潮流求解流程Fig.1 Flowchart of probabilistic power flow algorithm considering response correlation

4 算例分析

4.1 仿真算例参数

针对某省级电网（151个节点，252条支路）2014年2月23日18:00时的实时断面进行计算。该省风电资源较为丰富，110 kV及以上电网存在11个风电场接入点，风电场总出力为1354.3 MW，风电渗透率为11.2%。测试条件如下：假设风电节点和常规负荷节点均服从正态分布，波动标准差σ按期望值的不同百分比取定；不考虑各节点风电和常规负荷随机变量的相关性；电网中可调度的常规可调机组10台、柔性负荷4个，其接入节点、功率分配因子和基础出力如表1所示。

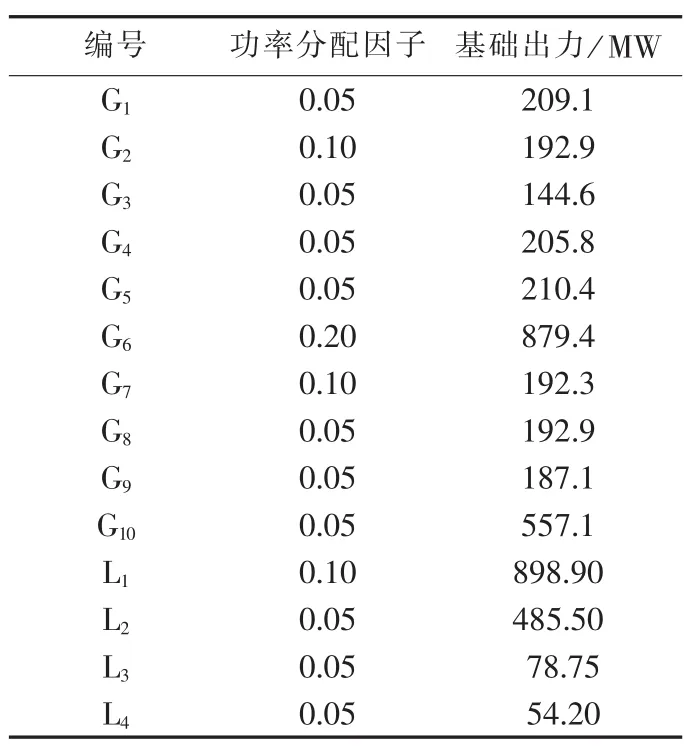
表1 可调度常规机组和柔性负荷信息Table 1 Information of schedulable conventional units and flexible loads

4.2 多场景下平衡节点累积概率分布情况

设计了以下4种不同场景：（1）风电波动为5%，负荷波动为2%；（2）风电波动为10%，负荷波动为2%；（3）风电波动为 20%，负荷波动为 5%；（4）风电波动为30%，负荷波动为5%。在不同场景下，分别采用基于半不变量的常规随机潮流法（简称为“常规随机潮流”，下同）与本文方法进行潮流计算，图2为不同场景下平衡节点（表1中机组G10）的有功功率累积概率分布情况。从图中可看出，随着风电和负荷随机性的不断增大，系统平衡机出力的随机性也不断增加。 此外，比较图2（a）、（b），使用常规随机潮流计算时平衡机的最大波动范围为［-400，1400］MW，机组G10将承担系统所有不平衡功率波动；采用本文方法，由于系统不平衡功率由表1中所有可调资源共同承担，机组 G10的最大波动范围为［510，610］MW，相对常规随机潮流小很多。图3为网内部分可调度机组和负荷的概率密度曲线，其中虚线为对应的初始功率期望值。随着风电和负荷随机性的不断增大，可调资源的响应随机性也逐渐增大。

图2 多种场景下平衡节点有功功率累积概率分布Fig.2 Cumulative probability distribution of active power of balancing bus for different scenarios

图3 部分可调度机组和负荷的概率密度曲线Fig.3 Probability density curves of schedulable unit 1 and flexible load 1

表2列出了各场景下对应的平衡节点出力越上限概率pup和越下限概率pdown。从表中可以看出，随着风电和负荷随机性的不断增加，使用常规随机潮流法时平衡节点出力越限概率逐渐上升，与实际电网运行情况不符。而使用本文方法计算时，原平衡节点的出力越限概率较小，与实际情况更加吻合。

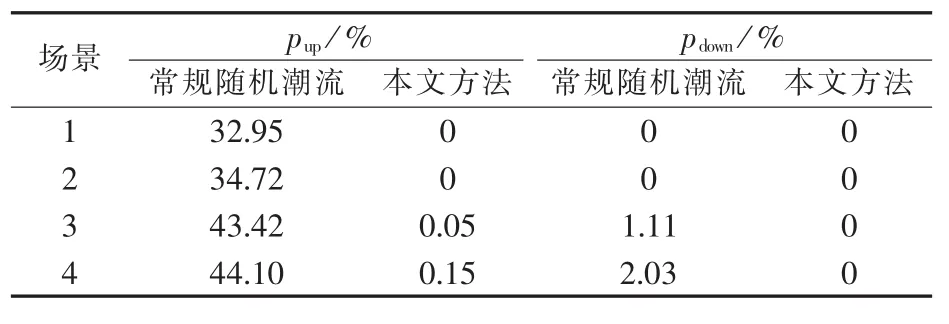
表2 多种场景下平衡节点有功出力越限概率Table 2 Active power limit violation probability of balancing bus for different scenarios

4.3 风电向上波动30%时可调度机组和柔性负荷的响应分析

通过可调度机组和柔性负荷响应能够平衡风功率和负荷波动的随机性，提升电网对风电的消纳能力。假设在场景3的基础上风电出力将向上波动30%，分别利用本文所提方法和蒙特卡洛法（抽样10000次）对可调度机组和柔性负荷的响应量情况进行分析，计算结果如表3所示。

从表中可知，本文方法与蒙特卡洛抽样法所得的可调资源的响应量期望和标准差非常接近。图4分别比较了系统各支路有功期望值和标准差的绝对误差，可以看出，2种方法结果非常接近，各支路有功期望值绝对误差最大不超过0.6 MW，标准差绝对误差最大不超过0.7 MW，其相对误差约为2%，验证了本文所提方法的正确性。

表3 2种方法下可调度机组和柔性负荷响应量的期望值和标准差Table 3 Expectation and standard deviation of schedulable unit response and flexible load response for two methods MW

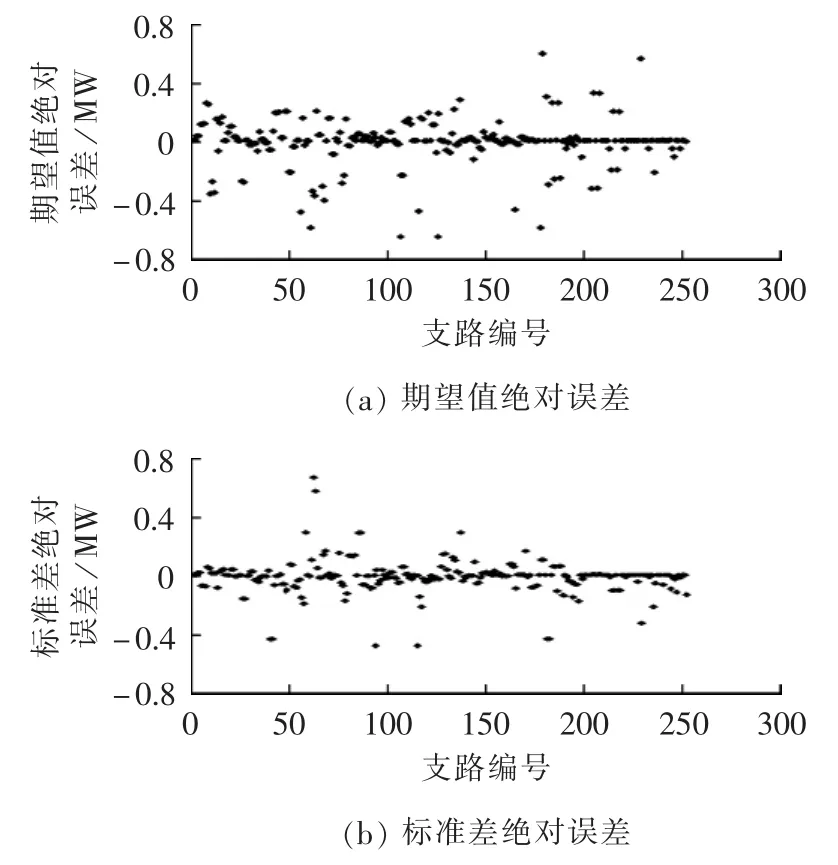
图4 各支路有功误差分析Fig.4 Error analysis of branch active power

4.4 方法性能分析

为进一步对本文方法的误差进行定量分析，采用方差和根均值ARMS（Average Root Mean Square）来度量本文所提方法的有效性，ARMS定义如下。

其中，MCm为蒙特卡洛所求累积概率分布曲线第m个点的值；pRm表示采用常规半不变量方法和采用本文所提方法时对应累积概率分布曲线第m个点的值；M为所取统计点总数，各点间距尽量小。本文设定蒙特卡洛抽样次数为10000次且计及功率在可调度机组和柔性负荷间的分配，节点电压、支路功率误差统计点总数M=1000。

表4列出了系统中部分节点的电压、支路功率的ARMS，并给出了系统电压、有功功率、无功功率的ARMS 最大值 AUM、APM、AQM和平均值 AUA、APA、AQA。 分析表4可得如下结论。

a.本文所得概率潮流结果误差均比常规半不变量概率潮流方法小一个数量级。由此表明，本文方法精度大幅提高，所得结果与蒙特卡洛方法基本一致。误差定量分析进一步验证了方法正确性。

b.耗时方面，本文方法速度稍慢于常规方法，主要原因在于计算过程中需要对不平衡功率进行分配并计及响应相关性。

c.经测试，蒙特卡洛方法耗时为274.6 s，而本文方法耗时仅0.265 s，因而相比蒙特卡洛法，本文方法在求解速度方面具有明显优势。

表4 方法性能分析结果Table 4 Results of method performance analysis

5 结论

随着智能电网的快速发展，为应对大规模间歇性能源带来的系统强随机性，源荷双侧可调度资源是实现系统供需瞬时平衡的有效有段。为了有效反映其对潮流分布的影响，本文提出了一种计及源荷双侧响应的概率潮流算法。首先，分析了系统不平衡功率与可调度资源响应量之间的概率表征方法；其次，所提概率模型合理分配了系统不平衡功率，使得计算结果不依赖于平衡节点的选择，结果更为准确。仿真算例结果表明，所提方法具有较好的实际应用价值，可为大规模间歇性能源并网后的系统分析、安全评估等提供参考依据。

［1］BURTON T，SHARPE D，JENKINS N，et al.Wind energy handbook［M］.Chichester，UK：John Wiley&Sons Ltd.，2001：12-39.

［2］韩民晓，崔军立，姚蜀军.大量风电引入电网时的频率控制特性［J］. 电力系统自动化，2008，32（1）：29-33.HAN Minxiao，CUI Junli，YAO Shujun.Frequency control characteristics for a power system with large amounts of wind power［J］.Automation of Electric Power Systems，2008，32（1）：29-33.

［3］BILLINON R，BAI G.Generating capacity adequacy associated with wind energy［J］.IEEE Trans on Energy Conversion，2004，19（3）：641-646.

［4］DA SILVA A M L L，SALES W S，DA FONSECA MANSO L A，et al.Long-term probabilistic evaluation of operating reserve requirements with renewable sources ［J］.IEEE Trans on Power Systems，2010，25（1）：106-116.

［5］陈炜，艾欣，吴涛，等.光伏并网发电系统对电网的影响研究综述［J］. 电力自动化设备，2013，33（2）：26-32，39.CHEN Wei，AI Xin，WU Tao，et al.Influence of grid-connected photovoltaic system on power network［J］.Electric Power Automation Equipment，2013，33（2）：26-32，39.

［6］姚建国，杨胜春，王珂，等.智能电网“源-网-荷”互动运行控制概念及研究框架［J］.电力系统自动化，2012，36（21）：1-6.YAO Jianguo，YANG Shengchun，WANG Ke，etal.Black-strat scheme evaluation indicator system and its application ［J］.Automation of Electric Power Systems，2012，36（21）：1-6.

［7］王卿然，谢国辉，张粒子.含风电系统的发用电一体化调度模型［J］. 电力系统自动化，2011，35（5）：15-18.WANG Qingran，XIE Guohui，ZHANG Lizi.An integrated generation-consumption dispatch model with wind power［J］.Automation of Electric Power Systems，2011，35（5）：15-18.

［8］刘文颖，文晶，谢昶，等.基于源荷互动的含风电场电力系统多目标模糊优化调度方法［J］.电力自动化设备，2014，34（10）：56-63.LIU Wenying，WEN Jing，XIE Chang，et al.Multi-objective fuzzy optimaldispatch based on source-load interaction forpower system with wind farm［J］.Electric Power Automation Equipment，2014，34（10）：56-63.

［9］高赐威，梁甜甜，李扬.节能发电调度下基于虚拟机组的日前负荷调度模型［J］. 中国电机工程学报，2014，34（22）：3691-3699.GAO Ciwei，LIANG Tiantian，LI Yang.Model of day-ahead load scheduling based on virtualgeneratorunitin energy-saving power generation dispatching［J］.Proceedings of the CSEE，2014，34（22）：3691-3699.

［10］王珂，刘建涛，姚建国，等.基于多代理技术的需求响应互动调度模型［J］. 电力系统自动化，2014，38（13）：121-127.WANG Ke，LIU Jiantao，YAO Jianguo，et al.Demand response interactive scheduling model based on multi-agent technology［J］.Automation of Electric Power Systems，2014，38（13）：121-127.

［11］王锡凡，王秀丽.电力系统随机潮流分析［J］.西安交通大学学报，1988，22（3）：87-97.WANG Xifan，WANG Xiuli.Probabilistic load flow analysis in power system［J］.Journal of Xi’an Jiaotong University，1988，22（3）：87-97.

［12］BORKOWSKA B.Probabilistic load flow ［J］.IEEE Trans on Power Apparatus and Systems，1974，93（3）：752-759.

［13］胡泽春，王锡凡.基于半不变量法的随机潮流误差分析［J］.电网技术，2009，33（18）：32-37.HU Zechun，WANG Xifan.Error analysis of the probabilistic load flow based on cumulantmethod ［J］. Power System Technology，2009，33（18）：32-37.

［14］郭效军，蔡德福.不同级数展开的半不变量法概率潮流计算比较分析［J］. 电力自动化设备，2013，33（12）：85-90.GUO Xiaojun，CAI Defu.Comparison of probabilistic load flow calculation based on cumulant method among different series expansions［J］.Electric Power Automation Equipment，2013，33（12）：85-90.

［15］MORALES J M，PEREZ-RUIZ J.Point estimate schemes to solve the probabilistic power flow［J］.IEEE Trans on Power Systems，2007，22（4）：1594-1601.

［16］吴晨曦，文福拴，陈勇，等.含有风电与光伏发电以及电动汽车的电力系统概率潮流［J］. 电力自动化设备，2013，33（10）：8-15.WU Chenxi，WEN Fushuan，CHEN Yong，etal.Probabilistic load flow ofpowersystem with WFs，PVsand PEVs ［J］.Electric Power Automation Equipment，2013，33（10）：8-15.

［17］彭寒梅，曹一家，黄小庆，等.基于组合抽样的含分布式电源随机潮流计算［J］.电力自动化设备，2014，34（5）：28-34.PENG Hanmei，CAO Yijia，HUANG Xiaoqing，et al.Probabilistic load flow calculation based on combination sampling for power system containing distributed generations ［J］.Electric Power Automation Equipment，2014，34（5）：28-34.

［18］方斯顿，程浩忠，徐国栋.基于Nataf变换和准蒙特卡洛模拟的随机潮流方法［J］.电力自动化设备，2015，35（8）：38-44.FANG Sidun，CHENG Haozhong，XU Guodong.Probabilistic load flow method based on Nataf transformation and quasi Monte Carlo simulation［J］.Electric Power Automation Equipment，2015，35（8）：38-44.

［19］丁明，李生虎，黄凯.基于蒙特卡罗模拟的概率潮流计算［J］.电网技术，2001，25（11）：10-14，22.DING Ming，LI Shenghu，HUANG Kai.Probabilistic load flow analysis based on Monte-Carlo simulation ［J］.Power System Technology，2001，25（11）：10-14，22.

［20］朱星阳，刘文霞，张建华，等.计及系统调频作用的随机潮流模型与算法［J］.中国电机工程学报，2014，34（1）：168-178.ZHU Xingyang，LIU Wenxia，ZHANG Jianhua，et al.Probabilistic load flow method considering function of frequency modulation［J］.Proceedings of the CSEE，2014，34（1）：168-178.

［21］余昆，曹一家，陈星莺，等.含分布式电源的地区电网概率潮流计算［J］. 中国电机工程学报，2011，31（1）：20-25.YU Kun，CAO Yijia，CHEN Xingying，et al.Dynamic probability power flow of district grid containing distributed generation［J］.Proceedings of the CSEE，2011，31（1）：20-25.

［22］WU Junli，ZHANG Buhan，LI Hang.Statistical distribution for wind power forecast error and itsapplication todetermine optimal size of energy storage system ［J］.Electrical Power and Energy Systems，2014，（55）：100-107.

［23］RAMANATHAN R，RAMCHANDANI H，SACKETT S A.Dynamic load flow techniqueforpowersystem simulators ［J］.IEEE Trans on Power Systems，1986，1（3）：25-30.