基于奇异值分解滤波与APES算法的异步电动机转子故障检测

许伯强，李金卜

（华北电力大学 电气与电子工程学院，河北 保定 071003）

0 引言

转子故障（如转子断条）是异步电机常见故障之一，在各类异步电机故障中约占10%，因此对其进行检测是十分必要的。

文献［1-2］阐明，当异步电机转子发生故障时，定子电流中会出现（1+2s）f1和（1-2s）f1（其中 s为转差率，f1为供电频率）频率的分量，这2个分量称为故障特征频率分量，它们可以作为转子故障检测的依据，而最常用的转子故障检测方法就是对定子电流信号进行频谱分析。但是，直接对定子电流信号进行频谱分析，特征频率分量可能因为f1分量的泄漏而被淹没，导致检测失败。对此文献［3］提出了解决这一问题的思路，即对平稳定子电流信号进行自适应滤波处理，将定子电流f1分量滤除，然后再进行傅里叶变换。文献［4］通过希尔伯特变换将f1分量转化成直流量，再对希尔伯特模量进行频谱分析。文献［5-6］避开电流信号对振动信号或位移信号进行频谱分析以检测故障。

在实际工程应用中，上述基于傅里叶变换的方法存在无法抑制噪声和因采样时间长而无法回避负荷波动的局限。为了达到频率分辨力的要求，必须保证足够长的采样时间（频率分辨力等于采样时长的倒数）。文献［7］提出了基于电机输出功率的检测方法，文献［8］通过分析逆变器驱动电机的逆变器直流侧的电流成分来判断转子是否发生故障，这2种方法并未基于定子电流信号进行频谱分析，回避了傅里叶变换。

现代信号处理技术的快速发展，为解决上述问题提供了新思路。ESPRIT、MUSIC、ARMA等算法已经广泛应用于诸多领域［9-11］，但这些算法本身并不具有估计幅值的能力，与最小二乘法结合寻找幅值时，往往受到背景噪声的影响，无法准确估计相应的幅值和相位。而故障特征频率分量的幅值对于故障严重程度的诊断十分必要。文献［12-13］将ESPRIT算法引入电机转子故障检测领域，为了估计故障特征频率分量的幅值，引入了优化算法。

本文将奇异值分解（SVD）滤波技术与幅度相位估计 APES（Amplitude and Phase EStimation）算法结合，提出了一种电机转子故障检测新方法。SVD滤波可以较好地滤除定子电流f1分量以突出故障特征频率分量，同时还可以滤除部分噪声。APES算法突破了傅里叶变换的局限，对于短时信号仍具有很高的频率分辨力，不仅能够准确估计故障特征频率分量的频率，而且能够计算其幅值和初相角。通过在一台Y100L-2型3 kW笼型异步电动机上进行试验，验证了所提方法的有效性。

1 SVD滤波技术

SVD是线性矩阵理论中一种非常有用的工具，并且已经广泛应用于工程领域，如信号滤波和矩阵秩的估计［14］。SVD是基于奇异值分类的算法，大奇异值对应能量较大或者能量集中的信号，相应地小奇异值对应能量较小或者能量分散的信号［15］。由文献［1-2］可知，f1分量的能量远远大于故障特征分量以及噪声的能量，因此通过SVD滤波技术可以滤除工频分量，同时可以滤除部分噪声。

对于一个一维的序列

构造Hankel矩阵：

其中，p+q-1=N，p＞q，N 为采样个数；H（i，j）=x（i+j-1）。

对矩阵H进行SVD：

其中，U1、∑1、V1对应着前几个较大的奇异值，是需要滤除的部分；上标H表示共轭转置。

重构滤波后的信号。假设为滤波后得到的信号矩阵，但这一信号矩阵并不等于真实信号构成的Hankel矩阵，与真实信号存在如下关系：

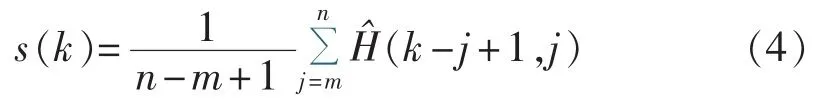
其中，m=max（1，k-p+1），n=min（q，k）。 即对信号矩阵斜对角线上的元素求平均值，可得到滤波后的信号序列（k）。

当采样点较多时采用上述方法编程不易实现，可以采用简便法［16］。简便法仅仅需要矩阵第一行和最后一列的数据，计算简单，原理清晰。

2 APES算法

20世纪90年代，Li等人提出了一种新的滤波器设计方法用于信号幅值和相位估计，也被称作APES 算法［17］。

假设输入信号为：

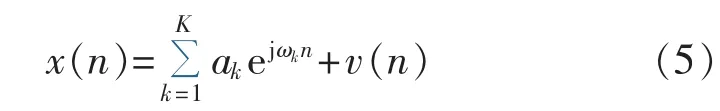
其中，ak和ωk分别为第k个信号的幅值和角频率；v（n）为加性白噪声。

考虑设计一个M抽头的FIR滤波器，使得期望角频率为ωk的信号无失真地通过滤波器，同时尽可能地抑制信号x（n）中的其他频率分量和噪声。分别定义向量

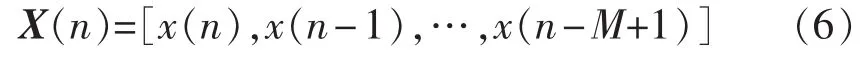
和滤波器权向量

要使角频率为ωk的信号无失真地通过滤波器，应有：

其中，为目标频率信号的采样点构成的向量。

通过计算可以将上述问题转化为约束优化问题：

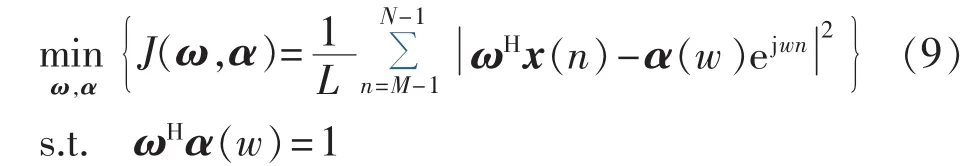
将目标函数展开有：

其中，L=N-M+1。

令：

将式（12）代入式（9）可以得到信号的幅度谱，即：

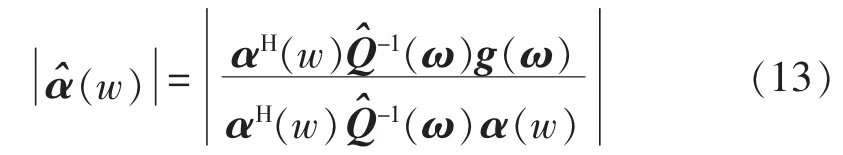
在频率会呈现一个峰值，而在其他频率点则会接近0。在得到信号的频率估计结果后，可以将其值回代到式（13）中得到频率为ω′的信号的复幅度估计结果（包括幅值和相位），这也是APES算法的由来。

3 SVD与APES算法相结合的仿真验证

设定子a相的仿真信号为：

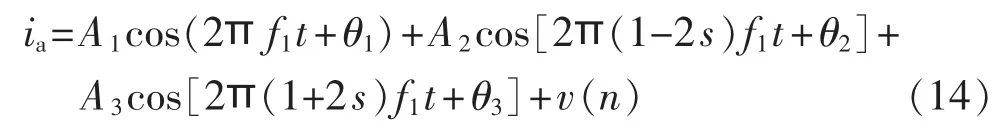
其中，A1=0.9 p.u.，A2=0.009 p.u.，A3=0.009 p.u.；s=0.016；θ1=0.3142 rad，θ2=1.0472 rad，θ3=2.8274 rad；f1=50 Hz；v（n）为有色噪声，信噪比为 50 dB。 图1 为仿真的定子电流信号，通过SVD滤波滤除f1分量以及部分噪声，处理后的电流波形i′a如图2所示。然后通过APES算法寻找故障特征分量，其幅值结果如图3所示。由图1—3可以看出，APES算法不但能够找到特征分量的频率，而且能够估计出相应的幅值。

图1 电流仿真信号Fig.1 Current signal for simulation

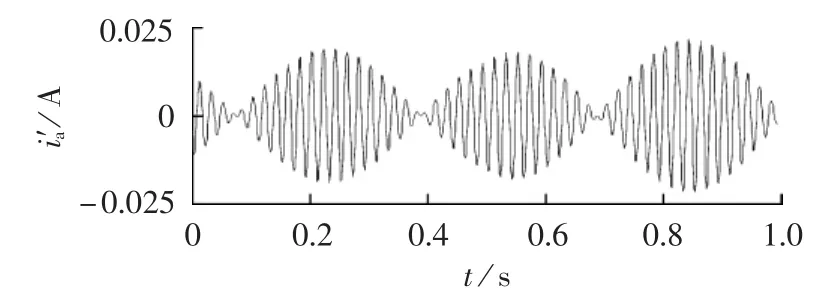
图2 滤除f1分量后的电流信号Fig.2 Current signal after f1component is filtered out

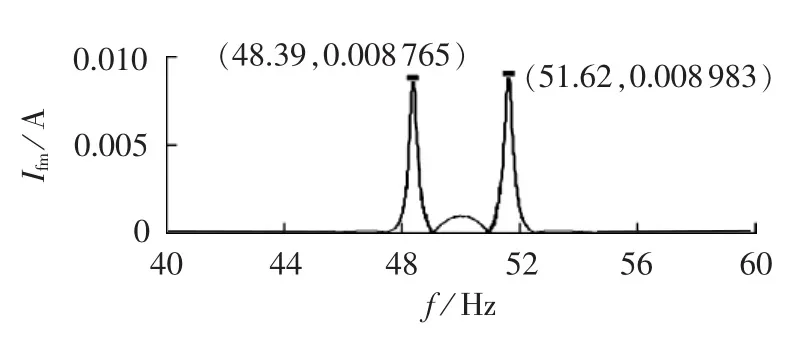
图3 特征频率分量Fig.3 Characteristic frequency components

4 SVD与APES算法相结合的异步电机故障检测新方法

4.1 方法流程

对该异步电机，本文所提故障检测方法的流程如下。

a.采集一相定子电流信号，采样频率为1000Hz，采样时长为1 s。

b.对采样信号进行SVD滤波，滤除f1分量，如果采样信号中噪声较大，可以再对滤除f1分量后的信号进行SVD滤波，滤除部分噪声。

c.对进行SVD滤波后的电流信号进行APES算法分析：检测信号中是否存在（1±2s）f1频率分量，计算（1±2 s）f1频率分量对应的幅值和初相角。根据（1±2s）f1频率分量及其幅值判断异步电机转子是否发生故障以及故障的严重程度。

4.2 试验结果

试验采用的三相异步电机型号为Y100L-2，额定容量为3 kW，额定电压为380 V，额定电流为6.12 A，额定频率为50 Hz，除正常的转子外，还配备一个故障转子以模拟断条故障，该故障转子存在一根断裂导条（距端环10 mm处钻孔，直径为6 mm、深度为 10 mm）。

图4为试验采集的a相定子电流幅值Iam，图5为经过SVD二级滤波滤除f1分量及部分噪声后的电流幅值 I′am。

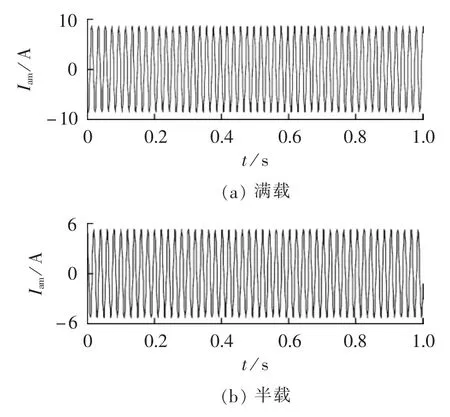
图4 原始电流波形Fig.4 Original current waveforms

图5 SVD滤波后的电流波形Fig.5 Current waveforms after SVD filtering

图6为故障电机在满载（s=3.6%）情况下，分别采用ESPRIT检测法与本文所提方法对定子a相电流进行频谱分析的结果。具体实验数据参见表1。

图6 满载情况下的试验结果Fig.6 Experimental results for full load condition

表1 满载情况下的试验数据Table 1 Experimental data for full load condition

图7（a）、（b）分别为故障电机在半载（s=1.8%）情况下，采用ESPRIT检测法与本文所提方法得到的定子a相电流的频谱图。具体试验数据参见表2。

对比图4与图5可以看出，SVD滤波有效滤除了电流信号中的工频分量，抑制了噪声。

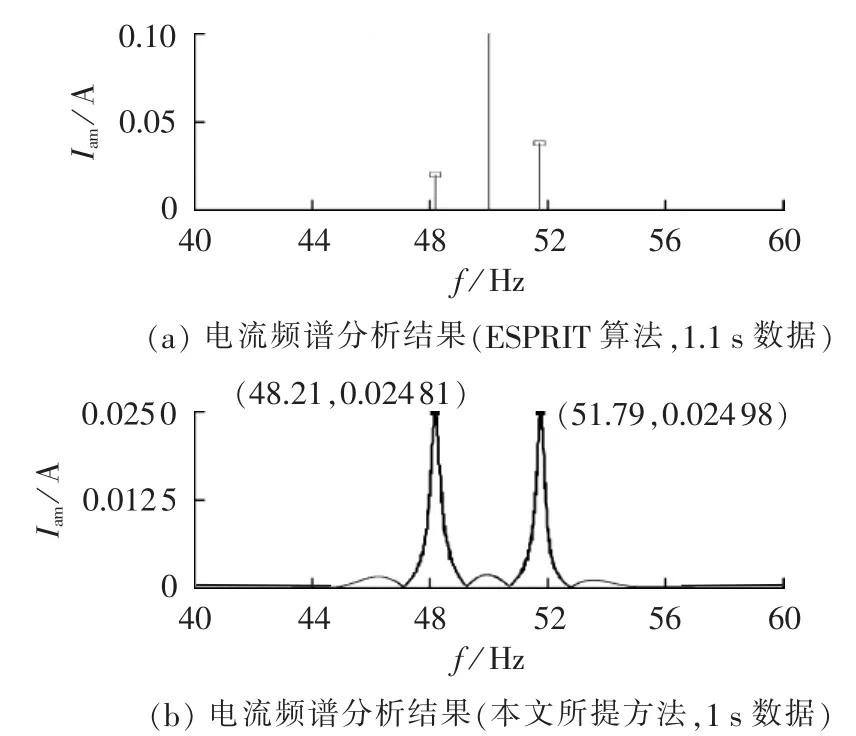
图7 半载情况下的试验结果Fig.7 Experimental results for half load condition

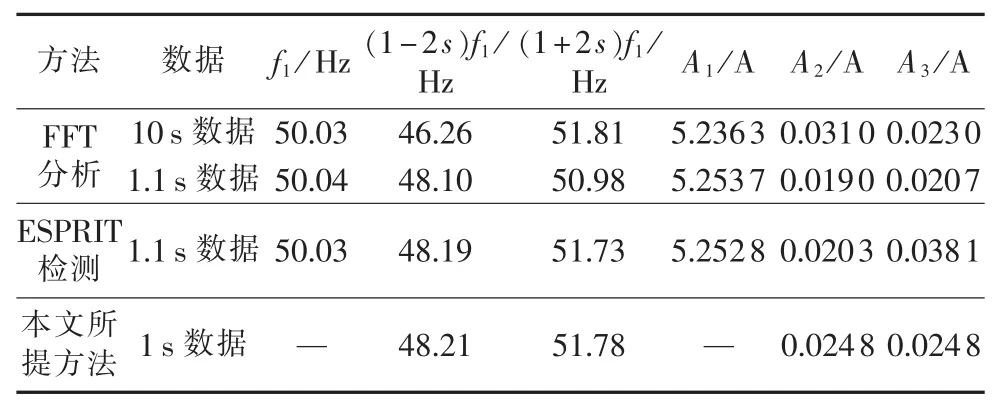
表2 半载情况下的试验数据Table 2 Experimental data for half load condition

从图6和表1中的数据可看出，在电机满载情况下，故障特征频率（3.6 Hz）偏离f1较远，因此对算法的频率分辨力要求较低，快速傅里叶变换（FFT）分析方法、ESPRIT检测法和本文所提方法的故障频率处理结果相互吻合，但是受噪声的影响，ESPRIT算法无法准确估计出特征频率对应的幅值。

从图7和表2中的数据可以看出，在电机半载情况下，FFT分析方法对10 s数据的分析结果、ESPRIT检测法和本文所提方法所得出的结果相吻合。但是随着转差率降低，FFT分析方法无法满足对短时数据的频率分辨力要求，从其对1.1 s数据的分析结果可以看出，其频率估计存在较大的误差，容易引起误判。而对于故障特征频率分量幅值的估计，FFT分析方法和本文所提方法的分析结果相吻合，而ESPRIT算法所估计的结果无法与真实值相匹配。因此，利用本文所提方法进行转子故障检测是可行的，而且仅仅需要1 s的短时数据，适用于负荷波动的情况。

5 结论

a.将SVD滤波技术与APES算法相结合提出了一种新的电机转子故障检测方法，对一台异步电机进行了转子故障检测试验，试验结果表明本文所提方法切实可行，可以应用于工程实际；

b.本文所提方法引入了SVD，滤除了f1分量，突出了故障特征分量，同时能够有效抑制噪声；

c.本文所提方法采用APES算法进行信号分析，突破了基于FFT算法的局限性——采样时间与频率分辨力之间的矛盾，对短时信号也可达到高频率分辨力的要求，且本身具有估计故障特征频率分量幅值的能力，可以有效地判断故障的严重程度。

［1］马宏忠，胡虔生，黄允凯，等.感应电机转子绕组故障仿真与实验研究［J］.中国电机工程学报，2003，23（4）：107-112.MA Hongzhong，HU Qiansheng，HUANG Yunkai，et al.Simulating and experiment studying on rotor winding fault of induction motor［J］.Proceedings of the CSEE，2003，23（4）：107-112.

［2］DELEROI W.Broken bar in squirrel cage rotor of an induction motor，part 1：description by superimposed fault currents［J］.Archivfür Elektrotechnik，1984（67）：91-99.

［3］姜建国，汪庆生，杨秉寿，等.用自适应方法提取鼠笼式异步电机转子断条的特征分量［J］. 电工技术学报，1996，11（4）：176-179.JIANG Jianguo，WANG Qingsheng，YANG Bingshou，et al.Applying the adaptive noise cancellation to extract the features of squirrel cage induction motor with rotor defects［J］.Transactions of China Electrotechnical Society，1996，11（4）：176-179.

［4］刘振兴，尹项根，张哲.基于Hilbert模量频谱分析的异步电动机转子故障在线监测与诊断方法［J］.中国电机工程学报，2003，23（7）：158-161.LIU Zhenxing，YIN Xianggen，ZHANG Zhe.Online rotor fault diagnosis in asynchronous motor based on Hilbert spectrum analysis of instantaneous power in asynchronous motor induction motors［J］.Proceedings of the CSEE，2003，23（7）：158-161.

［5］邹剑，陈进，朱军川，等.基于幅值与相角小波映射的裂纹转子故障诊断［J］. 机械工程学报，2003，39（2）：33-36.ZOU Jian，CHEN Jin，ZHU Junchuan，et al.Fault diagnosis of cracked rotor based on amplitude and phase wavelet map ［J］.Chinese Journal of Mechanical Engineering，2003，39（2）：33-36.

［6］陈敏，胡茑庆，秦国军，等.参数调节随机共振在机械系统早期故障检测中的应用［J］. 机械工程学报，2009，45（4）：131-135.CHEN Min，HU Niaoqing，QIN Guojun，et al.Application of parameter-tuning stochastic resonance for detecting early mechanical faults［J］.Journal of Mechanical Engineering，2009，45（4）：131-135.

［7］蒋建东，蔡泽祥.基于传输功率的感应电动机转子故障检测方法［J］. 电力自动化设备，2004，24（11）：37-38.JIANG Jiandong，CAI Zexiang.Detection of rotor cage fault based on output power signal for induction motor［J］.Electric Power Automation Equipment，2004，24（11）：37-38.

［8］胡文彪，夏立，向东阳，等.基于逆变器直流侧电流和融合算法的感应电机转子故障诊断方法［J］. 电力自动化设备，2011，31（8）：38-41.HU Wenbiao，XIA Li，XIANG Dongyang，et al.Rotor fault diagnosis based on DC-side current and fusion algorithm for induction motors［J］.Electric Power Automation Equipment，2011，31（8）：38-41.

［9］李天云，祝磊，宋莉，等.基于TLS-ESPRIT的同步电机参数辨识［J］. 电工技术学报，2009，24（12）：38-42.LI Tianyun，ZHU Lei，SONG Li，et al.Parameter identification of synchronous machine based on TLS-ESPRIT［J］.Transaction of China Electrotechnical Society，2009，24（12）：38-42.

［10］张静，徐政，牛卢璐.TLS-ESPRIT在电力系统信号高精度频谱估计中应用［J］. 电力自动化设备，2009，29（5）：48-51.ZHANG Jing，XU Zheng，NIU Lulu.Application of TLS-ESPRIT in high resolution spectrum estimation of power system signal［J］.Electric Power Automation Equipment，2009，29（5）：48-51.

［11］蒋平，吴熙，罗曦.基于TLS-ESPRIT算法的附加励磁阻尼控制抑制次同步振荡［J］. 电力自动化设备，2009，29（10）：25-29.JIANG Ping，WU Xi，LUO Xi.SSO mitigation using supplementary excitation damping controller based on TLS-ESPRIT ［J］.Electric Power Automation Equipment，2009，29（10）：25-29.

［12］孙丽玲，许伯强，李志远.基于旋转不变信号参数估计技术与模式搜索算法的异步电动机转子故障检测新方法［J］.机械工程学报，2012，48（13）：89-95.SUN Liling，XU Boqiang，LI Zhiyuan.Detection of rotor fault in induction motors by combining estimation of signal parameters via rotational invariance technique and pattern search algorithm［J］.Journal of Mechanical Engineering，2012，48（13）：89-95.

［13］许伯强，孙丽玲，李和明.基于高分辨力谱估计技术与优化算法的异步电动机转子故障检测新方法［J］.中国电机工程学报，2013，33（3）：140-147.XU Boqiang，SUN Liling，LI Heming.A detection method for rotor fault in induction motors based on high frequency resolution spectrum estimation technique and optimization algorithm［J］.Proceedings of the CSEE，2013，33（3）：140-147.

［14］张波，李健君.基于Hankel矩阵与奇异值分解（SVD）的滤波方法以及在飞机颤振试验数据预处理中的应用［J］.振动与冲击，2009，28（2）：162-166.ZHANG Bo，LI Jianjun.Denoising method based on Hankel matrix and SVD and its application in flight flutter testing data preprocessing［J］.Journal of Vibration and Shock，2009，28（2）：162-166.

［15］赵学智，叶邦彦，陈统坚.基于小波-奇异值分解差分谱的弱故障特征提取方法［J］. 机械工程学报，2012，48（7）：37-48.ZHAO Xuezhi，YE Bangyan，CHEN Tongjian.Extraction method of faint fault feature based on wavelet-SVD difference spectrum［J］.Journal of Mechanical Engineering，2012，48（7）：37-48.

［16］赵学智，叶邦彦.分量形成方式对奇异值分解信号处理效果的影响［J］. 上海交通大学学报，2011，45（3）：368-374.

ZHAO Xuezhi，YE Bangyan.The influence of formation manner of component on signal processing effect of singular value decomposition［J］.Journal of Shanghai Jiaotong University，2011，45（3）：368-374.

［17］何子述，夏威.现代数字信号处理及其应用［M］.北京：清华大学出版社，2009：5.