隐极发电机转子匝间短路时转子不平衡磁拉力的解析计算模型

张广韬，吴俊勇，李 扬，郝亮亮

（北京交通大学 电气工程学院，北京 100044）

0 引言

随着电力系统的不断发展，人们对同步发电机安全稳定运行的要求也越来越高。转子匝间短路是发电机常见的电气故障，小匝数的短路故障可能不会影响发电机的正常运行，但一旦故障发生蔓延，将导致发电机励磁电流增加，输出无功减小，机组振动加剧，烧伤轴颈和轴瓦，严重威胁发电机机组和电力系统的安全稳定运行［1-2］。

在电机中，机械与电气相互耦合，转子匝间短路故障会造成部分磁极短路，进而引起气隙磁场畸变，产生不同于正常运行时的气隙电磁力波和不平衡磁拉力，引起电机转子径向振动［3-4］。因此，不平衡磁拉力的准确计算与分析是实现基于振动或机电特征融合故障诊断的基础。

国外对不平衡磁拉力的研究起步较早，文献［5］认为发电机的气隙磁密和气隙长度成反比，并对不平衡磁拉力进行了讨论，在此基础上推导出了不平衡磁拉力的线性表达式。文献［6］针对磁饱和度对不平衡磁拉力的影响，对计算方程进行了进一步的改进。文献［7］通过实验研究证明了文献［2］计算方程的正确性。文献［8］和［9］用数值方法对电机发生偏心故障时的电磁力进行了计算，得到了与实验值较为吻合的结果。国内对不平衡磁拉力的研究多采用线性解析法和数值法，文献［10］对不同工况下转子偏心以及转子励磁绕组匝间短路造成的不平衡磁拉力进行了分析计算，并对转子偏心程度和励磁电流大小对不平衡磁拉力的影响进行了仿真分析；文献［11］分析了隐极同步发电机转子绕组匝间短路后励磁磁动势的变化规律，基于气隙磁导法对电机气隙磁场进行了分析，指出转子匝间短路故障使电机气隙磁场不对称，从而产生不平衡的磁拉力，通过计算得到定转子间的气隙磁导和气隙磁场能的解析式，进而得到作用于转子的不平衡磁拉力的表达式。但文献［10-11］在磁场分析过程中仅仅考虑了励磁电流对磁场的影响，没有考虑转子阻尼电流和定子电枢电流对磁场的影响。

本文针对常见的1对极汽轮发电机，提出通过对转子匝间短路故障时气隙磁场的解析计算得出转子所受不平衡磁拉力的方法。首先采用多回路法对A1552样机在额定运行时发生的转子匝间短路故障进行计算，得到了故障时定、转子电流的数值解，对样机进行了故障实验，并对实验结果与理论计算结果进行了对比；在此基础上，对发生匝间短路故障时的气隙磁动势和磁密进行了解析计算，并根据麦克维尔应力张量法计算出故障时转子所受到的不平衡磁拉力的大小和方向，得到了不平衡磁拉力的解析计算模型；最后利用ANSYS仿真软件建立了发电机有限元物理模型，对不平衡磁拉力进行了有限元计算，通过有限元计算与解析模型计算结果的对比验证了解析计算模型的正确性。

1 转子匝间短路故障时的各回路电流

采用交流电机的多回路理论计算转子匝间短路故障的基本思路是：首先以单个线圈为研究对象，得到每个线圈的电感参数，然后依照故障时各绕组的实际连接及组成方式，由有关线圈的参数计算出绕组回路参数［12-13］。该方法能够深入到定子相绕组和转子绕组内部，可计算出定子所有分支以及励磁绕组和阻尼回路的电流、电压［14-15］。

在充分考虑故障引起的励磁绕组电路拓扑结构改变和定子相绕组内部出现的不平衡电流的前提下，根据多回路理论列出了以定、转子所有回路电流为变量的状态方程［16-17］：

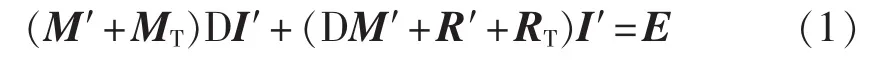
其中，M′和R′分别为回路电感矩阵和回路电阻矩阵，M′的值会随着定子与转子之间的相对运动而发生变化，为时变矩阵；MT和RT为常数矩阵，其数值与电网线路参数、变压器的电阻和漏感以及励磁系统的内电阻、内电感有关；列向量I′为定、转子各回路的电流，包括转子励磁绕组的正常回路和故障附加回路、阻尼回路以及定子电枢绕组回路的电流；列向量E由电网电压和励磁系统电源电压组成，为已知量；D为微分算子d／dt。式（1）为发生励磁绕组匝间短路故障时，同步发电机的多回路数学模型，采用适当的数值解法就可以求得故障时定、转子电流和电压的数值解，实现对故障的暂态仿真。下文的分析计算都以此模型的计算结果为基础。

2 转子匝间短路故障时气隙的磁动势和磁密

2.1 转子励磁电流产生的气隙磁动势

隐极同步电机每极下的励磁绕组由节距不等的分布式同心式线圈串联而成，设转子空间坐标xr的起点为转子d轴，每个同心式线圈单独产生的磁动势均为分布在整个电机气隙圆周、关于d轴中心线对称的矩形波，如图1所示。

图1 励磁绕组同心式线圈产生的磁动势Fig.1 Magnetomotive force produced by concentric field coil of field windings

励磁绕组第 h（h=1，2，3，…）个同心式线圈产生的气隙磁动势ffd，h的表达式为：

其中，yh和nr，h分别为第h个同心式线圈的节距和匝数；αh，1和αh，2为同心式线圈的 2 个边所对应的转子坐标电角度。

当同步发电机发生励磁绕组匝间短路后，励磁绕组被分为正常励磁回路（电流为if）和励磁故障附加回路［18］（电流为 ifkL），如图2所示。

图2 励磁绕组匝间短路时励磁回路示意图Fig.2 Schematic diagram of excitation loop during inter-turn short circuit of excitation winding

图2中，EZF为励磁电动势；RZF为励磁电源内阻；RfkL为励磁短接线电阻。虽然转子发生匝间短路故障后，励磁电流除了含有直流分量，还有一定成分的交流分量，但是由于交流分量很小，在此不再考虑其对气隙磁场的影响［19］。故障绕组在气隙中产生的磁动势ffd，hf等效于正常励磁回路产生的磁动势和故障附加回路产生的反向磁动势的叠加，如式（3）所示。

其中，ffd，n，hf和ffd，f，hf分别为第 hf个故障线圈的正常励磁回路和故障附加回路产生的磁动势。

2.2 转子阻尼电流产生的气隙磁动势

同步电机的阻尼绕组一般是由阻尼条组成的笼形回路，如图3所示。

图3 阻尼回路结构示意图Fig.3 Schematic diagram of damping loop structure

与励磁绕组不同，阻尼绕组中的电流不含直流分量，只有交流谐波分量。 第 j（j=1，2，…，Nd，其中Nd为转子所有阻尼回路个数的总和）个阻尼回路的k次谐波电流的表达式为：

其中，ω 为同步角频率；t为时间；Id，j，k和φd，j，k分别为第j个阻尼回路k（对于常见的1对极发电机而言，k的值为6的倍数［20］）次谐波电流的有效值和相位。

id，j，k在气隙中产生的磁动势为：

其中，yd，j为第 j个阻尼回路的节距；αd，j，1和αd，j，2为第j个阻尼回路的2个边所对应转子坐标电角度；nd为阻尼回路线圈匝数。进而可以得到整个转子所有的阻尼回路在气隙中产生的磁动势：

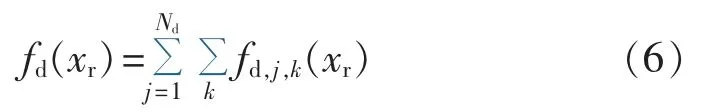
2.3 定子电枢电流产生的气隙磁动势

同步发电机正常联网带负载运行时，定子分支中的电流以基波为主；在发生励磁绕组匝间短路故障后，虽然定子绕组依然是正常的，但故障励磁绕组所产生的空间谐波磁场会在定子绕组内部感应2、4等偶数次谐波不平衡电流［21］。定子坐标和定子各槽位置图如图4所示。

将定子空间坐标xs的零点放置在定子1号槽的中心线上，取逆时针方向为xs的正方向，如图4所示。则定子电枢 a 相 ai（i=1，2，…，Na，其中 Na为 a 相分支的总数）分支的第 j（ j=1，2，…，Nai，其中 Nai为 a相ai分支线圈的总数）个线圈的k次谐波电流的表达式为：

其在气隙中产生的磁动势为：

图4 定子坐标和定子各槽位置图Fig.4 Stator coordinates and stator slot positions

其中，ys为定子绕组线圈节距；ns为线圈匝数；αs，ai，j，1和αs，ai，j，2为线圈的2个边所对应的定子坐标电角度。进而可以得到定子a相电流产生的磁动势和abc三相电流产生的磁动势：

2.4 转子匝间短路故障时的气隙磁密

为了方便计算，将2.1—2.3节的计算结果都转换到定子坐标系中，设γ0为转子d轴与定子坐标系轴线在t=0时的电角度，γ为转子位置角，即转子d轴逆时针旋转超前定子坐标轴线的电角度，则有：

当转子匀速旋转时，γ=ωt+γ0，将 xr换成 xs-γ，就能得到故障时气隙磁动势的表达式为：

其中，ffd（xs-γ）为所有励磁线圈产生的磁动势。

对于均匀磁路，根据式（12）可以进一步得到发生短路故障时气隙磁密的计算公式［22］：

其中，λ=μ／l表示单位面积的磁导，称为导磁系数，μ为气隙的磁导率，l为等效气隙长度。

3 发生匝间短路故障时转子不平衡磁拉力解析

发电机发生匝间短路故障时，气隙中的磁场就不再对称，转子就会受到不平衡磁拉力的作用。不平衡磁拉力可以分为径向磁拉力和切向磁拉力，但径向磁拉力要比切向磁拉力的值大很多。所以，本文只研究转子所受的径向磁拉力，不再考虑切向磁拉力［21］。基于2.4节计算得到的故障时气隙磁密的分布情况，利用Maxwell应力张量法可以得到沿发电机圆周任意位置的径向分布电磁力的密度（单位为N／m2）如下：

其中，Br和μ0分别为径向磁密和空气磁导率。

计算转子受到的不平衡磁拉力需要对式（14）沿转子表面闭合路径进行积分：

其中，Drotor为转子直径；Lrotor为转子铁芯的长度。

利用数值法对式（15）进行积分求解，需要对连续数据进行离散化处理，可以在此路径上均匀取Nδ个离散单元，每个离散单元对应的定子坐标电角度为 xs，m（m=1，2，…，Nδ），计算得到每个单元所受的径向磁拉力为：

其中，Δxs为相邻的2个离散单元对应的定子坐标电角度差。

由式（16）可得到径向磁拉力在全局坐标系下X轴和Y轴方向的分力，叠加后即为转子在X轴和Y轴方向受到的不平衡磁拉力FX和FY。

在得到FX和FY的基础上，还可以进一步求出不平衡磁拉力的模值FUMP和方向αUMP（αUMP为不平衡磁拉力与全局坐标系X轴的夹角）：

4 仿真验证

为了验证对故障时转子所受不平衡磁拉力的解析计算的准确性，本文利用ANSYS仿真软件对A1552样机建立了有限元模型，并对解析模型与有限元模型的计算结果进行了对比。

4.1 仿真模型与计算步骤

4.1.1 实验方法

为验证多回路数学模型计算联网负载时1对极A1552样机发生励磁绕组匝间短路故障的精度，需要利用实验样机进行发电机转子匝间短路实验。实验样机A1552转子的结构示意图如图5所示。图中，转子为2极的叠片铁芯，包括等间隔的24个槽，实际励磁槽数为20个，每极下有2个空槽；每极都有5个励磁同心线圈，放置在两两对称的10个励磁槽中，励磁绕组串联总匝数为660。A1552样机在励磁绕组的内部引出了7个抽头，除了首末端2个抽头外，另5个抽头用于进行励磁绕组匝间短路实验使用。A1552样机的参数为：额定容量为12 kW；额定电压为400V；额定励磁电流为8.5A，空载励磁电流为6A；额定功率因数为0.8（滞后）；额定频率为50 Hz；极对数为1；气隙长度为1.5 mm；定子每相并联支路数为2；定子每支路串联线圈数为6；定子线圈节距为15；定子每槽导体数为12；转子槽分度数为24；励磁绕组每极串联匝数为330；励磁绕组并联支路为1；转子实槽数为20；转子每极阻尼条数为7。

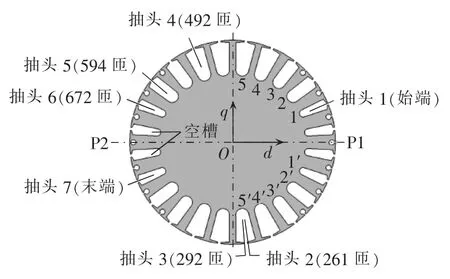
图5 A1552实验样机转子冲片和励磁绕组引出的抽头Fig.5 Rotor lamination and field winding taps of prototype A1552

选择如此多的匝数进行实验对比是为了尽量排除电机制造因素带来的仿真与计算的偏差。联网负载时，样机a2分支电流的多回路法得到的仿真波形和实验波形如图6所示。由图可见，仿真波形和实验波形吻合良好。

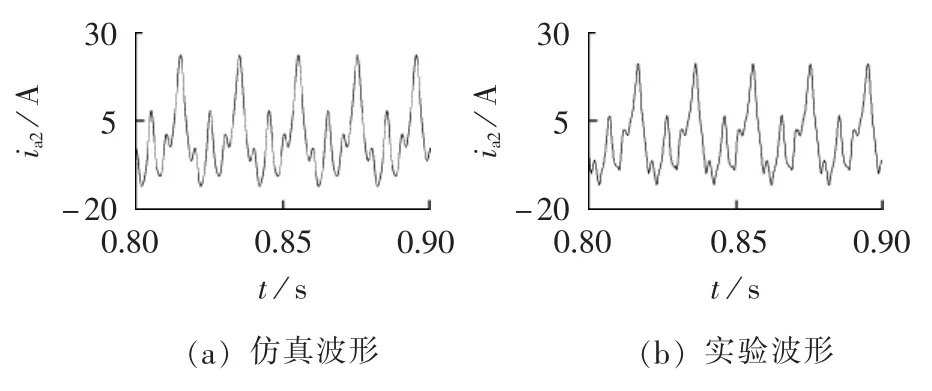
图6 联网负载时，发生2-4抽头短路故障情况下的a2分支电流波形Fig.6 Current waveforms of Branch a2 when short circuit occurs between Tap 2 and 4，in grid-connecting condition

为进一步验证场多回路法计算的精确度，用FFT分析得到实验中定、转子稳态电流的各次谐波分量有效值，并与计算的稳态值进行对比，同时也给出了多回路法计算的各次谐波分量，如表1所示。

由表1可以看出，实验结果和利用多回路法得到的计算结果吻合较好，验证了数学模型计算1对极同步发电机联网时发生励磁绕组匝间短路故障的正确性。在此基础上，继续利用多回路法计算发生励磁绕组匝间短路故障时转子阻尼回路和定子电枢的稳态电流有效值和相位，结果分别如表2和表3所示。

表1 联网负载时，发生2-4抽头短路故障情况下，稳态电流各次谐波分量Table1 Harmonic components of steady-state current when short circuit occurs between Tap 2 and 4，in grid-connecting condition

表2 转子阻尼回路的稳态电流有效值和相位的实验值Table 2 Experimental RMS and phase of steady-state currents of rotor damping loops

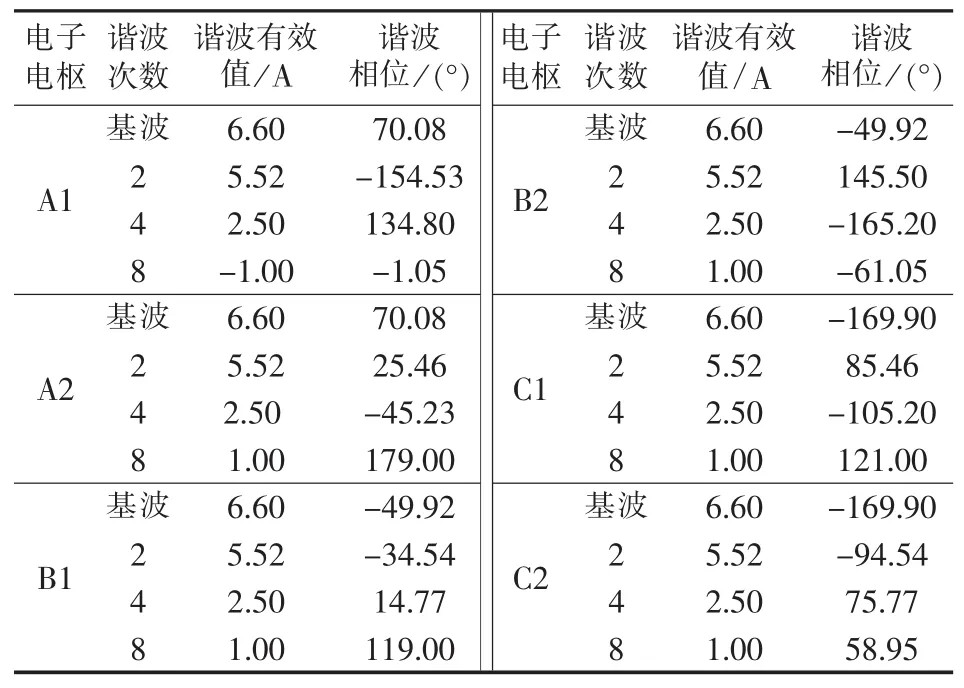
表3 定子电枢的稳态电流有效值和相位的实验值Table 3 Experimental RMS and phase of steady-state currents of stator armatures

4.1.2 发电机的有限元模型

以隐极式发电机A1552样机为例，进行有限元建模。

本文利用有限元分析软件ANSYS建立了A1552样机的整个横截面的二维有限元物理模型，见图7。

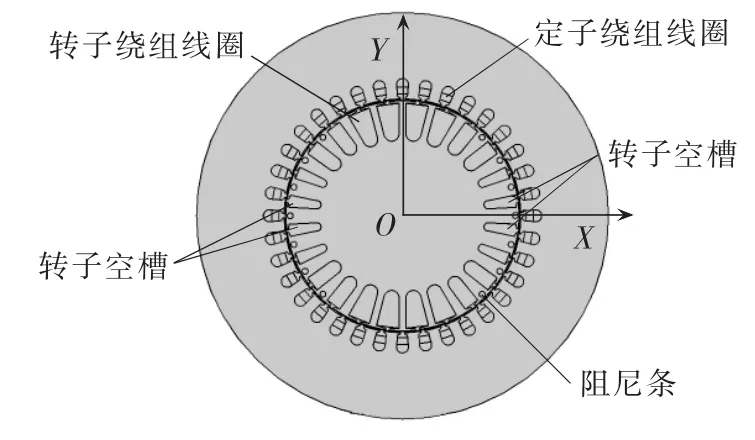
图7 发电机有限元物理模型Fig.7 Finite element model of generator

在建立有限元模型时，作如下假定：

a.不考虑位移电流和静态自由电荷，认为电位移矢量随时间的变化率对曲面的积分为零，即电磁场为似稳场；

b.不考虑发电机的端部效应，认为磁场在Z轴方向上分布均匀；

c.忽略铁磁材料的磁滞效应，认为铁芯单向同性，具有单值的B-H曲线；

d.进行静态磁场分析，不考虑磁场随时间的变化效应，如涡流等。

由于采用静态磁场分析，所以某时刻电机内的磁场视为恒定磁场，引入矢量磁位A表示磁通密度B，根据亥姆霍兹定理，得：

其中，为哈密尔顿算子。

对于XY坐标系内的二维平面场，设电流密度和矢量磁位只有Z轴方向的分量，因而采用矢量磁位AZ建立的发电机二维磁场的数学模型为：

其中，μ为磁导率；JZ为电流密度的Z轴分量；AZ0为边界τ的已知值，符合第一类边界条件。考虑到铁芯磁导远大于空气磁导，认为几乎没有磁通穿过定子外表面，磁力线在定子外表面处与边界平行，即认为矢量磁位A沿铁芯表面切线方向没有变化，满足AZ0=0。

模型采用六节点的三角形网格进行了智能剖分，由于气隙内的磁场分布情况是分析线圈耦合参数的关键，为保证剖分密度，将剖分起始位置设置在气隙处。剖分后的模型如图8所示。在所剖分的每一个单元中，保存的材料磁导都认为是固定不变的，所以每一个单元都满足式（21）的Ω磁场描述。

图8 三角形剖分的有限元模型Fig.8 Finite element model meshed by triangle elements

4.1.3 有限元法分析不平衡磁拉力的步骤

采用有限元法分析短路故障下转子所受的不平衡磁拉力的步骤如下：

a.利用多回路法计算A1552样机联网负载条件下发生转子匝间短路故障时的转子励磁电流、阻尼电流和定子电枢电流等相关运行数据；

b.根据实际尺寸建立发电机的二维有限元物理模型；

c.将步骤a得到的运行数据导入步骤b建立的有限元物理模型，计算发生匝间短路故障时发电机内部电磁场，得到沿气隙圆周各个单元的磁密并保存；

d.计算励磁绕组匝间短路故障发生时沿转子表面各个单元所受的电磁力和整个转子所受的不平衡磁拉力；

e.改变转子位置，重复步骤c、d，直到转子旋转一周为止。

另外，模型在气隙的中心位置设置了一条气隙线，通过该气隙线将气隙分为定子气隙和转子气隙两部分。通过对定、转子气隙分界线上的节点组成不同的耦合点集，实现转子的自动旋转，而不需要修改原始的物理模型。

4.2 解析模型计算和有限元计算结果的对比分析

通过建立发电机的数学模型和物理模型，并利用解析模型计算和有限元计算2种方法，在转子发生匝间短路时，求取了气隙磁密的分布情况和转子受到的不平衡磁拉力，结果如图9—13所示。

图9 发生匝间短路故障时气隙的磁密分布Fig.9 Flux density distribution of air-gap during inter-turn short circuit

图10 发生匝间短路故障时转子所受的X轴向不平衡磁拉力Fig.10 X-axial unbalanced magnetic pull of rotor during inter-turn short circuit

图9为由解析模型计算和有限元计算2种方法得到的同步发电机发生转子匝间短路故障时气隙磁 密的分布情况，此时转子位置角γ=0°；图10和图11分别为转子受到的不平衡磁拉力在X轴和Y轴方向的分量；图12和图13分别为不平衡磁拉力的方向和模值，可以看出此不平衡磁拉力与转子同步旋转，转子旋转一周，其幅值周期性地变化6次。由图9—13可以看出，利用2种方法得到的结果吻合良好，验证了不平衡磁拉力解析计算模型的正确性。此外，整个有限元计算过程耗时长达2 h，而整个解析模型计算过程仅耗时1 min，充分证明了解析模型计算相比于有限元计算耗时更短、效率更高。

4.3 不平衡磁拉力的影响因素分析

4.3.1 故障位置对不平衡磁拉力的影响

为研究不同的短路位置对转子受到的不平衡磁拉力的影响，分别计算转子的11′—55′同心式线圈分别发生5匝短路故障时转子受到的不平衡磁拉力，计算时选取额定工况，转子位置角γ=0°（下文相同），结果如表4所示。

由表4的结果可以看出，在短路匝数相同的前提下，故障位置越靠近磁极大齿，即转子的d轴，转子受到的不平衡磁拉力越大。

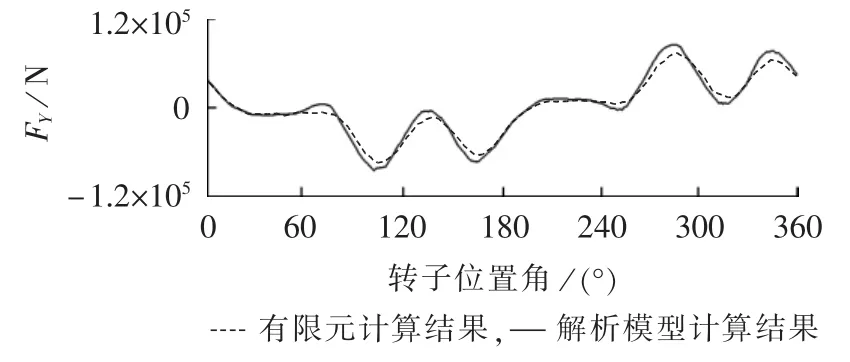
图11 发生匝间短路故障时转子所受的Y轴向不平衡磁拉力Fig.11 Y-axial unbalanced magnetic pull of rotor during inter-turn short circuit

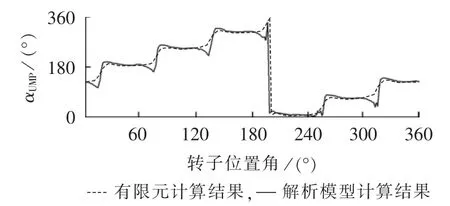
图12 发生匝间短路故障时转子所受不平衡磁拉力的方向Fig.12 Direction of unbalanced magnetic pull of rotor during inter-turn short circuit

图13 发生匝间短路故障时转子所受不平衡磁拉力的大小Fig.13 Magnitude of unbalanced magnetic pull of rotor during inter-turn short circuit

表4 不平衡磁拉力随短路位置的变化情况Table 4 Variation of unbalanced magnetic pull along with short circuit location

4.3.2 短路匝数对不平衡磁拉力的影响

为探讨短路匝数对不平衡磁拉力的影响，对A1552样机励磁绕组同心式线圈11′发生不同匝数的短路故障时转子所受到的不平衡磁拉力进行了计算，结果如图14所示。

图14 不平衡磁拉力随短路匝数的变化情况Fig.14 Variation of unbalanced magnetic pull along with short circuit turns

由图14可见，在故障位置确定的前提下，短路匝数和转子受到的不平衡磁拉力呈近似线性关系，不平衡磁拉力的模值随着短路匝数的增加而增加。

5 结论

本文采用解析模型计算和有限元计算2种方法对1对极隐极同步发电机发生励磁绕组匝间短路故障进行计算，将2种方法得到的结果进行对比，验证了本文所提解析模型计算的正确性和高效性。在此基础上又对匝间短路故障位置和短路匝数等因素对不平衡磁拉力的影响进行了分析，得出了以下结论：

（1）短路匝数相同的前提下，故障位置越靠近磁极大齿，转子受到的不平衡磁拉力越大；

（2）故障位置确定的前提下，短路匝数和转子受到的不平衡磁拉力呈近似的线性正相关关系。

本文研究将在一定程度上有助于改变大型汽轮发电机转子匝间短路故障在线诊断中转子不平衡磁拉力难以测量的问题，大幅提高匝间短路故障在线诊断的效率。

［1］郝亮亮，孙宇光，邱阿瑞，等.大型水轮发电机励磁绕组匝间短路的稳态故障特征分析［J］. 电力系统自动化，2011，35（4）：40-45.HAO Liangliang，SUN Yuguang，QIU Arui，et al.The steady-state fault characteristics of large hydro-generator with inter-turn short circuit of field windings［J］.Automation of Electric Power Systems，2011，35（4）：40-45.

［2］郝亮亮，孙宇光，邱阿瑞，等.同步发电机励磁绕组匝间短路时的电磁转矩［J］. 电力系统自动化，2011，35（16）：59-65.HAO Liangliang，SUN Yuguang，QIU Arui，et al.Electromagnetic torque of synchronous generator with inter-turn short circuit in the field winding［J］.Automation of Electric Power Systems，2011，35（16）：59-65.

［3］郝亮亮，吴俊勇.同步发电机匝间短路故障在线监测的研究评述与展望［J］. 电力自动化设备，2013，33（9）：144-150.HAO Liangliang，WU Junyong.Review and prospect of online rotor inter-turn short-circuit monitoring for synchronous generator［J］.Electric Power Automation Equipment，2013，33 （9）：144-150.

［4］张征平，刘石.大型汽轮发电机转子匝间短路故障在线诊断方法［J］. 电力自动化设备，2012，32（8）：148-152.ZHANG Zhengping，LIU Shi.Online diagnosis of interturn short circuit for large turbine generator’s rotor［J］.Electric Power Automation Equipment，2012，32（8）：148-152.

［5］BEHREND B A.On the mechanical force in dynamos caused by magnetic attraction［J］.Transactions of the American Institute of Electrical Engineers，1900，XVⅡ：613-633.

［6］COVO A.Unbalanced magnetic pull in induction motors with eccentric rotors［J］.Transactions of the American Institute of Electrical Engineer，1954，73（2）：1421-1425.

［7］TENHUNEN A，HOLOPAINEN T P，ARKKIO A.Effects of satuation on the forces in induction motors with whirling cage rotor［J］.IEEE Transactions on Magnetics，2004，40（2）：766-769.

［8］TCNHUNEN A.Finite-element calculation of unbalanced magnetic pulland circulating currentbetween parallelwindings in induction motor windings non-unifom eccentricity motor［C］∥Proceedings of Electromotion.Bologla，Italy：IEEE，2011：1676-1682.

［9］TCNHUNEN A，BENEDETTI T，HOLOPAINEN T P，et al.Electromagnetic forces in cage induction motors with rotor eccentricity［C］∥Proceedings of IEEE IEMDC.Madison，USA：IEEE，2003：1616-1622.

［10］周理兵，马志云.大型水轮发电机不同工况下不平衡磁拉力［J］.大电机技术，2002（2）：26-29.ZHOU Libing，MA Zhiyun.Unbalanlced magnetic in large hydro-generator for different operating conditions［J］.Large Electric Machine and Hydraulic Turbine，2002（2）：26-29.

［11］赵艳军，李永刚，武玉才，等.汽轮发电机转子匝间短路时转子振动特性分析［J］. 华北电力大学学报，2008，35（9）：16-21.ZHAO Yanjun，LI Yonggang，WU Yucai，et al.Analysis of rotor vibration characteristic for turbine generator rotor winding inter-turn short circuit fault［J］.Journal of North China Electric Power University，2008，35（9）：16-21.

［12］HAO Liangliang，SUN Yuguang，QIU Arui，etal.Steady-state calculation and online monitoring of interturn short circuit of field windings in synchronous machines［J］.IEEE Transactions on Energy Conversion，2012，27（1）：128-138.

［13］HAO Liangliang，SUN Yuguang，QIU Arui.Analysis on the negative sequence impedance directional protection for stator internal fault of turbo generator［C］∥Proccedings of the 13th InternationalConference on Electrical Machines and Systems.Incheon，South Korea：IEEE，2010：1421-1424.

［14］孙宇光，郝亮亮，王祥珩.同步发电机励磁绕组匝间短路的数学模型与故障特征［J］. 电力系统自动化，2011，35（6）：45-50.SUN Yuguang，HAO Liangliang，WANG Xiangheng.Math model and fault characteristics of field winding inter-turn short circuit of synchronous generator［J］.Automation of Electric Power Systems，2011，35（6）：45-50.

［15］孙宇光，郝亮亮，王祥珩.隐极同步发电机励磁绕组匝间短路的多回路电感参数计算［J］. 电力系统自动化，2010，34（13）：55-60.SUN Yuguang，HAO Liangliang，WANG Xiangheng.Calculation of the multi-loop inductances for inter-turn short circuits of field windings in non-salient pole synchronous machines ［J］.Automation of Electric Power Systems，2010，34（13）：55-60.

［16］孙宇光，王祥珩，桂林，等.同步发电机励磁绕组匝间短路的仿真研究［J］.电工电能新技术，2008，27（2）：5-10.SUN Yuguang，WANG Xiangheng，GUILin，etal.Simulation research on inter-turn shortcircuits offield windings in synchronous machines［J］.Advanced Technology of Electrical Engineering and Energy，2008，27（2）：5-10.

［17］郝亮亮.同步发电机励磁绕组匝间短路故障计算及在线监测［D］. 北京：清华大学，2012.HAO Liangliang.Calculation and online monitoring of interturn short circuit of field windings in synchronous generator［D］.Beijing：Tsinghua University，2012.

［18］郝亮亮，孙宇光，邱阿瑞，等.同步发电机励磁绕组匝间短路故障稳态数学模型及仿真［J］. 电力系统自动化，2010，34（18）：51-56.HAO Liangliang，SUN Yuguang，QIU Arui，et al.Steady-state mathematical and simulation of inter-turn short circuit of field windings in synchronous machines［J］.Automation of Electric Power Systems，2010，34（18）：51-56.

［19］孙宇光，郝亮亮，王祥珩.同步发电机励磁绕组匝间短路故障时的稳态电流谐波特征研究［J］.中国电机工程学报，2010，30（33）：51-57.SUN Yuguang，HAO Liangliang，WANG Xiangheng.Steady-state currents harmonic characteristics of synchronous machine with inter-turn short circuits of field windings［J］.Proceedings of the CSEE，2010，30（33）：51-57.

［20］郝亮亮，吴俊勇，陈占锋.转子匝间短路故障对大型汽轮发电机振动的影响机理［J］. 电力系统自动化，2014，38（4）：25-31.HAO Liangliang，WU Junyong，CHEN Zhanfeng.Mechanism of effects of inter-turn short circuits in field windings on large turbogenerator vibration［J］.Automation of Electric Power Systems，2014，38（4）：25-31.

［21］郝亮亮，孙宇光，邱阿瑞，等.隐极发电机励磁绕组匝间短路故障定位及短路匝数估算［J］. 中国电机工程学报，2011，31（21）：85-92.HAO Liangliang，SUN Yuguang，QIU Arui，et al.Fault location and short circuit turns estimation of inter-turn short circuits of field windings in non-salient-pole synchronous generator［J］.Proceedings of the CSEE，2011，31（21）：85-92.

［22］高景德，王祥珩，李发海，等.交流电机及其系统的分析［M］.北京：清华大学出版社，2005：5-6.