基于复杂网络社团聚类的复合故障特征分离诊断方法
2016-05-20陈安华莫志军蒋玲莉
陈安华, 莫志军, 蒋玲莉, 潘 阳
(湖南科技大学 机械设备健康维护湖南省重点实验室,湖南 湘潭 411201)
基于复杂网络社团聚类的复合故障特征分离诊断方法
陈安华, 莫志军, 蒋玲莉, 潘阳
(湖南科技大学 机械设备健康维护湖南省重点实验室,湖南 湘潭411201)
摘要:针对复合故障多种故障特征相互叠加彼此干扰,给全面准确诊断带来困难,提出了基于复杂网络社团聚类的复合故障特征分离诊断方法。该方法首先应用EMD将复合故障信号分解为若干个IMF分量,由于不同单一故障的特征会在不同频段得以体现,提取每个IMF分量的特征量,建立故障数据网络模型;然后将每个IMF分量视为网络中的社团,根据复杂网络社团结构的特性,进行同类社团合并,合并所得每个社团与单一故障相对应,最后对合并的信号进行分析,实现复合故障特征分离。以转子不平衡和轴承内圈、轴承内圈和滚动体复合故障特征分离与诊断为例,验证了该方法的可行性。
关键词:复杂网络;社团聚类;复合故障;特征分离;故障诊断
随着工业技术的进步,大型复杂机械正朝着大型化、复杂化发展,机械运行状态是否良好将直接影响工业生产。然而在工程实际中有的设备零件需要损坏达到一定程度才更换,在载荷工况极其复杂情况下,此期间可能出现多种故障并存的现象,从而形成复合故障[1-2]。由于大部分复合故障的特征频率均处于分析频率的低频段,能量较低,常被淹没在强大的背景噪声中,故障间的相互影响等特性,从频谱图上很难看出与故障对应的特征频率。因此,给复合故障全面准确诊断造成困难。而近几年,对单故障诊断研究发展迅速,如FFT(Fast Fourier Transform)分析、包络谱分析、小波分析、谱峭度等[3-6],这些方法在单故障诊断中均表现出较好的效果。然而,将这些方法应用于复合故障诊断中却会遇到许多困难,FFT分析和包络谱分析在诊断故障强弱差距较大的复合故障时,较弱的故障成分容易淹没于噪声之中,从而在诊断时被忽略。小波分析通过特定的基函数对信号特征进行提取,在故障诊断中广泛应用的是单小波且只有一个基函数,只能最佳匹配一种故障特征,故在复合故障特征提取时容易顾此失彼。谱峭度是根据计算每根谱线的峭度值大小来选取带通滤波器参数,然后进行故障诊断,在分析复合故障时,由于选取最大的峭度值进行分析导致某些故障峭度值易被遗漏,从而难以准确诊断出各故障状态。因此,如何将复合故障特征分离从而形成单一故障进行故障诊断,一直是难点且缺乏行之有效的分离方法,同时也成为故障诊断中需要解决的关键问题。
近年来,复杂网络研究受到越来越多的关注,并从自然科学渗透到工程科学甚至机械故障诊断等多个领域,已成为一个新的研究方向。杜海峰等[7]研究了利用网络表示数据结构,通过网络结构反映故障状态及其特征,提出了基于网络结构分析的故障诊断策略,并对四级压缩机故障诊断获得了很好的正确率。张爱萍等[8]研究了复杂网络在船舶柴油机故障诊断,把轮机故障数据样本视为复杂网络,这就将故障诊断中聚类问题转化为复杂网络社团聚类,诊断结果正确率高并能识别未知故障。复杂网络是对复杂系统抽象的描述方式,任何包含大量组成单元的复杂系统,当把构成单元抽象成节点,单元之间的相互关系抽象为边时,都可以当作复杂网络。对于机械故障诊断,将每个故障样本视为网络中的节点,由于同种故障样本之间的联系比较紧密,不同故障样本之间的联系稀疏,这样就可以将相同故障视为网络中的社团结构[9-10]。通过社团聚类,以实现准确聚类诊断。
EMD(Empirical Mode Decompsition)作为一种新的主成分分析法[11-13],可以根据被分析信号本身特点,自适应选择频带确定信号在不同频段的分辨率。复合故障中不同故障信号的频谱结构和特征时间尺度不同。EMD依据信号的特征时间尺度分解信号,得到本征模态函数IMF(Intrinsic Mode Faction)1,IMF2,IMF3,…,IMFn,分别反映信号中内嵌的简单振荡模式,依次包含从高到低的信号频率成分,这样复合故障振动信号中的各故障状态信息会在不同IMF分量频段中得以体现。然后将每个IMF分量视为复杂网络中的社团结构进行社团聚类,将相同故障特征IMF分量合并,从而实现复合故障特征分离诊断。因此,本文提出了基于复杂网络社团聚类的复合故障特征分离诊断方法。
1复杂网络社团聚类复合故障特征分离
1.1故障数据的网络模型
通过现场监测,获得复合故障动态信息,对复合故障观测信号进行经验模态分解,得到若干个IMF分量,提取不同IMF分量特征量,组成样本集,把每个样本抽象为网络节点,样本与样本之间的关系抽象为边,这样不同IMF分量的样本就可以抽象成复杂网络结构,而每个IMF分量视为网络中的社团。
设故障样本集X={x1,x2,…,xn},每个样本p个属性,即xi={xi1,xi2,…,xip},(i=1,2,…,n),xi与xj之间的联系用相似度aij∈A表示;将每个数据样本xi视为网络“节点”,数据样本之间的联系作为网络“关系”,则数据结构可以表示成加权无向网络G(X,A)。
比较不同模式的相似性可以转化为比较两个向量的距离。一般而言,aij是样本xi和xj间距离dij的函数。相似度函数设计的原则是使网络具有较好的块状结构(块内相似度尽可能接近,块之间相似度差别较大),将其定义为:
aij=exp(-λ*dij)
(1)
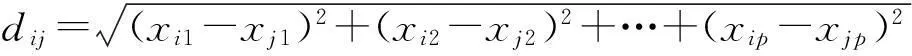
式中:dij为欧式距离度量。显然,dij越小,aij越大,表明xi与xj间的相似度越大。由于样本自身的相似度没有意义,本文定义自身的相似度为0,即当i=j时,aij=0。由于两个节点之间彼此的相似度相等,即aij=aji,所以A是一个对称矩阵。则n个节点的网络的连接矩阵为:
(3)
至此,得到加权无向网络模型G(X,A)。
1.2复杂网络聚类系数
复杂网络聚类系数[14-15]揭示了网络的聚类特性,节点i的聚类系数Ci表示与i相连接的节点中任意两个节点之间存在连接的概率。若节点i与ki个节点相连,这ki个相邻节点之间最多存在ki(ki-1)/2条边。Ei是相邻节点之间实际存在的边数,则:
(4)
网络的聚类系数C为整个网络中所有节点的聚类系数的平均值:
(5)
复杂网络具有社团结构特性,当聚类系数越大,网络的聚类程度越高,设置在不同的判别因子φ时,计算对应的每个社团聚类系数,从而确定判别因子φ,当aij大于φ设置为1,表示两个节点之间有联系;小于φ就设置为0 ,表示两个节点之间没有联系。这样网络就可以抽象为由点集和边集组成的图来表示。
1.3复杂网络社团聚类
将复合故障信号经EMD分解的IMF分量视为网络中社团,通过同类社团合并,将合并的IMF重新组合进行频谱分析,最终实现复合故障特征分离。
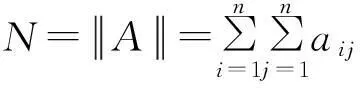
(6)

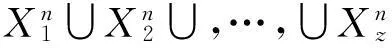
(7)


(8)
式中:Δφpq∈φn,p,q=1,2,…,z。
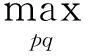
(9)

归纳上述原理和过程,基于复杂网络社团聚类的复合故障诊断模型见图1。

图1 基于复杂网络社团聚类复合故障特征分离诊断流程图Fig.1 Diagnosis flow chart based on complex network community cluster compound fault feature separation
2实例分析
为了验证本文提出方法的有效性,采用机械故障综合模拟实验台作为模拟不平衡-轴承内圈、轴承内圈-滚动体两种复合故障运行环境(见图2)。实验台由3马力变频调速电机驱动转子—轴承系统,采用PULSE高精度测试系统及振动加速度传感器4514-B-001分别安装在轴承座的x,y,z三个方向。

图2 机械故障综合模拟实验台Fig.2 Mechanical fault comprehensive simulation experiment
2.1转子不平衡和轴承内圈复合故障诊断
在机械故障综合模拟实验台上,轴两端一端安装正常轴承,另一端安装内圈故障轴承;轴承型号为ER10K,轴承的节径D=33.5 mm,滚动体直径d=7.94 mm,滚动体个数Z=8,接触角α=00;在转盘上增加两个质量为6 g的螺丝钉,构造转子不平衡和轴承
内圈复合故障。轴的转速为2 396 r/min,采样频率为16 384 Hz,根据故障特征频率计算公式,经计算在该工况下滚动轴承内圈故障特征频率fi=197.1 Hz,转子不平衡故障的特征频率为40 Hz(见图3)。

图3 内圈故障和转子不平衡Fig.3 Inner fault and rotor Unbalanced
在搭建的实验台上进行振动信号采集,该复合故障信号的时域和频域信号(见图4),从频谱图上难以识别出转子不平衡故障特征频率和轴承内圈故障特征频率,从而并不能判断是否含有复合故障。应用本文提出的将复合故障信号特征分离进行分析,首先利用EMD方法对采集的复合故障振动信号进行分解,计算分解所得IMF分量的时域特征量,每个IMF分量提取10个样本,分解结果(见图5)。
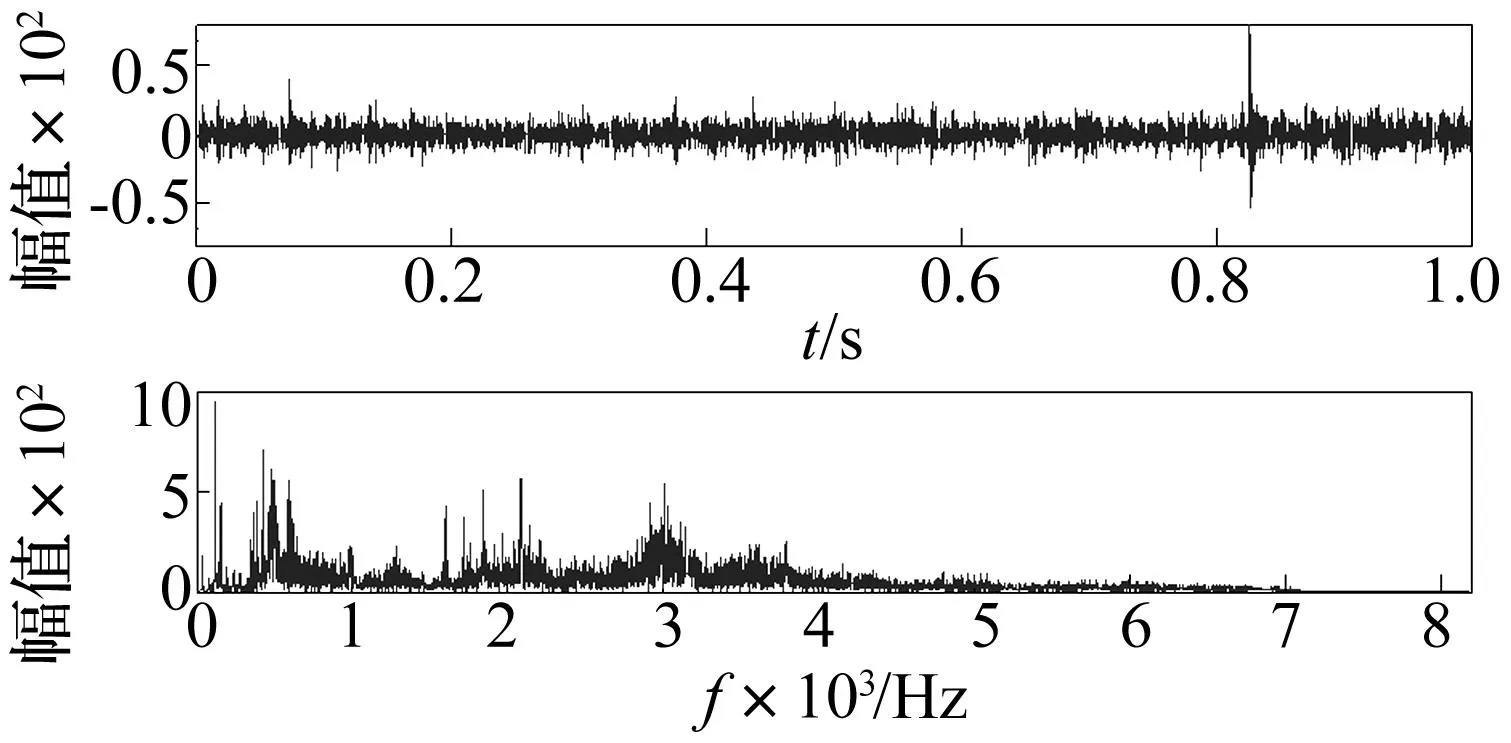
图4 不平衡-内圈故障复合故障时域和频域图Fig.4 Rotor Unbalanced-Inner ring compound fault time domain and frequency domain

图5 EMD分解结果Fig.5 The results of EMD decomposition
将分解所得的IMF分量视为复杂网络中社团,每个样本作为复杂网络中的一个节点,将样本与样本之间联系抽象为边,建立具有120个节点的复杂网络模型G(X,A)。根据式(1)和式(2)计算节点与节点之间的关系,建立相似度矩阵A。计算网络模型中每个社团的平均聚类系数C从而选择因子φ,因子φ从0.45开始,以步长0.05递增。从图6可知,当φ=0.6时大部分社团聚类系数值下降较明显,由于聚类系数越高,网络的聚类程度越好,因此,该文选择φ=0.6,从而建立的故障数据网络模型,其网络连接矩阵A。

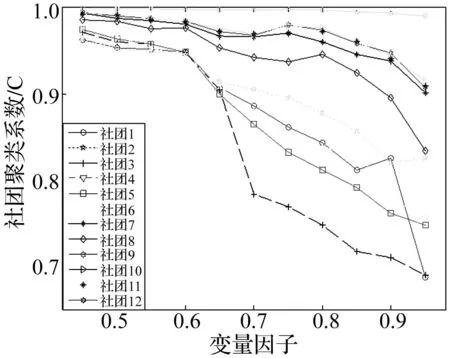
图6 社团聚类系数Fig.6 Community clustering coefficient

由上述合并结果可以看出,IMF1,IMF2,IMF3,IMF4,IMF5合并在一起,剩下IMF分量合并在一起,合并结果分析见图7。
针对分离后的信号进行包络谱分析,(见图7(a)所示,可以看到谱峰值192.1 Hz,该值与内圈故障特征频率197.1 Hz非常接近以及2倍频、3倍频清晰可见,表明轴承中存在内圈故障。(见图7(b)),谱峰值40 Hz以及倍频十分明显,表明转子存在不平衡故障。这与实验相符。

图7 内圈和转子不平衡复合故障分离的包络谱图Fig.7 Envelope spectrum of inner and rotor Unbalance composite fault separation
2.2轴承内圈和滚动体复合故障诊断
在机械故障综合模拟实验台上,设置内圈和滚动体复合故障轴承,轴的转速为1 798 r/min,采样频率为16 384 Hz,经计算在该工况下滚动轴承内圈故障和滚动体故障特征频率分别为fi=150.2 Hz、f0=60.5 Hz,其故障件见图8。

图8 轴承内圈和滚动体故障Fig.8 Bearing inner and ball fault
在实验台上采集该复合故障轴承的振动信号,利用本文提出的基于复杂网络社团聚类方法对复合故障信号进行分离。根据合并指标变化Δφ,并将IMF1,IMF2,IMF3,IMF5合并在一起,剩下的IMF分量合并在一起,对分离的信号进行包络谱分析见图9。
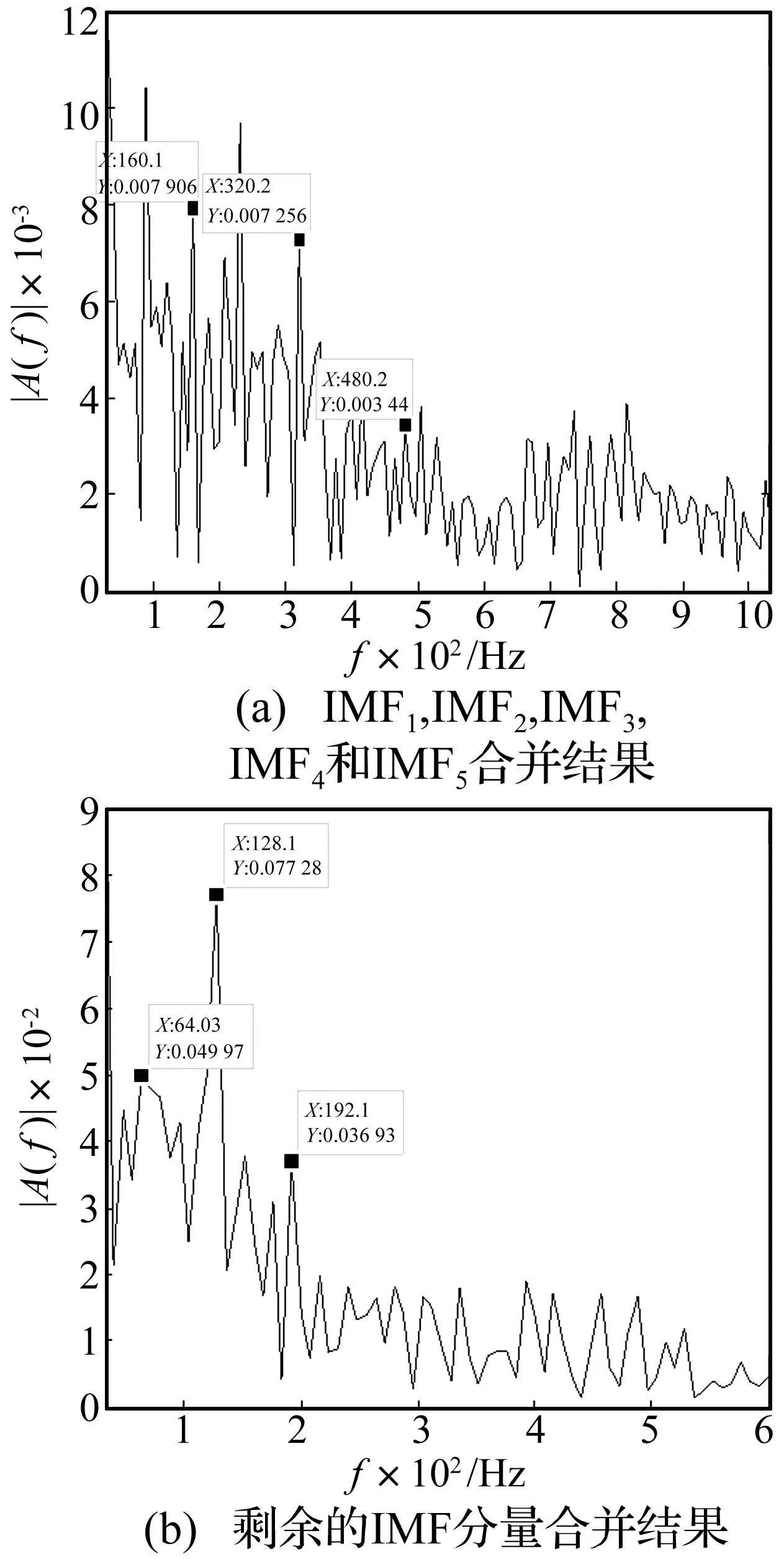
图9 轴承内圈和滚动体复合故障分离的包络频谱图Fig.9 Envelope spectrum of inner and ball composite fault separation
针对分离后的信号进行包络谱分析(见图9(a)),谱峰值160.1 Hz与内圈故障特征频率150.2 Hz接近,以及2倍频和3倍频(320.2 Hz≈2 fi,480.2 Hz≈3 fi),表明轴承中存在内圈故障。图9(b)中谱峰值64.03 Hz与滚动体故障特征频率60.5 Hz非常接近,并且有十分明显的2倍频,3倍频特征 (128.1 Hz≈2 fi,192.1 Hz≈3 fi),而且随着整数倍的增加,峰值的大小单调下降,这一结果表明轴承中存在滚动体故障,与实验结果相符。
综上可见,应用所提出的基于复杂网络社团聚类方法对不平衡-内圈复合故障、轴承内圈-滚动体复合故障诊断,对分离后的信号进行分析,所得结果符合各自故障规律且能准确反映复合故障信息源,验证了提出的方法可以将复合故障特征进行分离,从而为解决复合故障诊断提供一个新的方法。
3结论
针对复合故障诊断困难问题,提出了一种基于复杂网络社团聚类的复合故障特征分离诊断方法。该方法首先采用EMD将复合故障信号分解为若干个IMF分量,提取每个IMF分量的特征量,建立故障数据网络模型;然后将每个IMF分量视为网络中的社团,根据复杂网络社团结构的特性,进行同类社团合并;并对合并的信号进行分析,得到分离后的单故障信号,从而实现复合故障特征分离。应用本方法对转子不平衡和轴承内圈、轴承内圈和滚动体两类复合故障诊断,通过实验验证该方法能准确地将复合故障特征分离,提取各自的故障特征,表明本方法为复合故障诊断提供了一个新的途径。
参 考 文 献
[ 1 ] 明安波,褚福磊,张炜. 滚动轴承复合故障特征分离的小波-频谱自相关方法[J].机械工程学报,2013,49(3): 80-86.
MING An-bo,CHU Fu-lei,ZHANG Wei.Compound fault features separation of rolling element bearing based on the wavelet decomposition and spectrum auto-correlation[J]. Journal of Mechanical Engineering,2013,49(3): 80-86.
[ 2 ] Tang Gui-ji, He Yu-ling, Wan Shu-ting, et al. Investigation on stator vibration characteristics under air-gap eccentricity and rotor short circuit composite faults[J].The Brazilian Society of Mechanical Sciences and Engineering,2014,36:511-522.
[ 3 ] 蒋刚,肖建,郑永康,等.一种改进的快速傅里叶变换算法及其在故障诊断中的应用[J]. 计算机应用,2006, 26(2): 448-450.
JIANG Gang, XIAO Jian, ZHENG Yong-kang, et al.Fixed structure FFT algorithm and application in fault diagn-oses[J].Computer Applications,2006, 26(2): 448-450.
[ 4 ] Jing Tian, Morillo C, Pecht M G. Rolling element bearing fault diagnosis using simulated annealing optimized spectral kurtosis[J].Center for Advanced Life Engineering, 2013:1-5.
[ 5 ] 段晨东,何正嘉. 基于提升模式的特征小波构造及其应用[J].振动工程学报,2007,20(1):85-90.
DUAN Chen-dong, HE Zheng-jia. Characterized wavelet constr-uction based on lifting scheme and its applications[J].Journal of Vibration Engineering,2007,20(1):85-90.
[ 6 ] Antoni J. The spectral kurtosis:A useful tool for characterizing non-stationary signals[J]. Mechanical Systems and Signal Processing,2006,20(2):282-307.
[ 7 ] 杜海峰,王娜,张进华,等.基于复杂网络的故障诊断策略[J].机械工程学报,2010,46(3): 90-96.
DU Hai-feng, WANG Na, ZHANG Jin-hua,et al.Fault diagnosis strategy based on complex network analysis[J].Journal of Mechanical Engineering,2010,46(3): 90-96.
[ 8 ] 张爱萍.复杂网络的仿真研究及在轮机系统中的应用[D].大连:大连海事大学,2010.
[ 9 ] Newman M E J. The structure andfunction of complex network[J].SIAM Review, 2003,45(2):167-256.
[10] Li Xiang-hua, Gao Chao, Pu Ru-yang. A community clustering algorithm based on genetic algorithm with novel coding scheme[J].International Conference on Natural Computation,2014,10: 486-491.
[11] Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Royal Society of London Proceedings Series A,1998,454(3):1971.
[12] 蒋玲莉,刘义伦,李学军,等.EMD-模糊聚类法及在滚动轴承故障诊断中的应用[J].机械强度,2011,33(1):650-654.
JIANG Ling-li,LIU Yi-lun, LI Xue-jun,et al.Fault diagnosis of roller bearing based on EMD and Fuzzy cluster[J].Journal of Mechanical Strength,2011,33(1):650-654.
[13] Zhao Ling, Chu Xiao-yan, Huang Da-rong. Fault diagnosis for gearbox based on EMD and multiracial[J].Chinese Control and Decision Conference,2014,26:3792-3796.
[14] 汪小帆,李翔,陈关荣.复杂网络理论及其应用[M].北京:清华大学出版社,2006.
[15] Tabak B M, Takami M, Rocha J M C, et al. Directed clustering coefficient as a measure of systemic risk in complex banking networks[J]. Physica A: Statistical Mechanics and its Applications, 2014, 394: 211-216.
[16] Newman M E J. Fast algorithm for detecting community structure in networks[J].Phys Rev.E,2004(69):1-5.
[17] 杜海峰,悦中山,李树茁,等.基于模块性指标的动态网络社群结构探测方法[J].系统工程理论与实践,2009, 29(3):163-171.
DU Hai-feng, YUE Zhons-shan, Ll Shu-zhuo,et al.Community structure detecting algorithm for dynamic networks based on modularity[J].Systems Engineering-Theory & Practice,2009, 29(3):163-171.
Composite fault features separation diagnosis method based on complex network organization clustering
CHENAn-hua,MOZhi-jun,JIANGLing-li,PANYang(Hunan Provincial Key Laboratory of Health Maintenance for Mechanical Equipment, Hunan University of Science and Technology, Xiantan 411201, China)
Abstract:The diagnosis of composite faults in mechanical systems is a challenge at present. Due to features of composite faults interfering, it is hard to diagnose composite faults fully and accurately. Here, a diagnosis method for composite fault features separation based on complex network organization clustering. Firstly, a faulty signal was decomposed into several intrinsic mode functions (IMFs) with empirical mode decomposition (EMD). As different single-fault characteristic could be reflected in different frequency ranges, the characteristics of each IMF component were extracted and the network model of fault data was built. Each IMF was taken as an organization in the network. According to the characteristics of complex network organizations structure, the organizations in the same type were merged. The merged organization corresponded to a single fault. At last, the separation of composite fault features was realized for the decomposed signal. Taking rotor unbalance and bearing inner race, and bearing inner race and bearing roller composite fault characteristics separation and diagnosis as an example, the feasibility of this method was verified.
Key words:complex network; organization clustering; composite fault; characteristics separation; fault diagnosis
中图分类号:TH-39;TP391
文献标志码:A
DOI:10.13465/j.cnki.jvs.2016.07.012
通信作者莫志军 男,硕士生,1992年生
收稿日期:2015-01-29修改稿收到日期:2015-03-17
基金项目:国家自然科学基金资助项目(51175169);国家高新技术研究发展计划(2012AA041805);湖南省教育厅科学研究优秀青年项目(14B057);湖南省教育厅科学研究重点项目(13A023)
第一作者 陈安华 男,教授,博士生导师,1963年生
E-mail:184753404@qq.com
