改进的LMD方法及其在滚动轴承故障诊断中的应用研究

李　琳， 张永祥， 明廷锋(海军工程大学 船舶与动力学院，武汉　430033)



改进的LMD方法及其在滚动轴承故障诊断中的应用研究

李琳， 张永祥， 明廷锋(海军工程大学 船舶与动力学院，武汉430033)

摘要：针对局部均值分解(Local Mean Decomposition, LMD)方法存在的端点效应问题，提出一种基于梯度变化的端点效应抑制方法对局部均值分解进行改进，通过仿真对比不同端点抑制方法的效果，证明了该方法的准确性；针对滚动轴承故障振动信号为一系列调制信号的特点，将改进的局部均值分解方法应用于滚动轴承故障诊断中；利用奇异值分解降噪方法降低噪声污染对分解结果的影响；通过实验验证了该方法在滚动轴承故障诊断中的有效性和可行性。

关键词：局部均值分解；端点效应；奇异值分解；滚动轴承；故障诊断

当滚动轴承出现故障时，机械故障振动信号往往表现为一定的调制形式，其实际故障振动信号通常为多个调幅调频信号的叠加。通过对信号的解调，可以有效地提取出故障特征，因此信号解调方法在滚动轴承故障诊断中取得了广泛的应用[1-4]。但目前常用的滚动轴承诊断方法，如共振解调技术、EMD方法等都存在一定得不足。局部均值分解(Local Mean Decomposition,LMD)是2004年提出的一种新的自适应信号分析方法，它可以自适应地把信号分解为一系列具有明显物理意义的单分量的调幅调频信号与残余分量之和，因此该方法又相当于一种信号解调方法。该方法克服了Hilbert变换中存在的负频率问题，并且相对于EMD方法，它更好的解决了模态混叠问题，因此在滚动轴承的故障诊断中具有广阔的应用前景[5-6]。

端点效应是各种信号分解算法都无法避免的一个问题，LMD相对于EMD而言，虽然在端点效应处理上得到了改进，但端点效应的影响依然很明显，并且在噪声污染较为严重时，分解的准确性较低，因此，本研究针对这一问题，提出新的端点效应抑制方法，并通过仿真和实验的方法予以验证。实验结果表明，该方法可以有效抑制LMD分解过程中端点效应的影响，成功实现对滚动轴承的故障诊断。

1LMD方法的改进

LMD在分解过程中，以信号序列的极值点为插值点，以三次样条插值函数拟合信号上下包络线，得到信号包络线均值。但由于有限长信号序列端点处的极值点的不确定，包络线拟合时在序列两端难以确定包络线的拟合趋势，会出现发散现象，拟合的上下包络线以及包络线均值会产生拟合误差，并且误差会随着分解层数的增多而逐渐增大，使分解结果严重失真。为了抑制端点效应导致的分解误差，本文提出一种基于梯度延拓的端点效应处理方法。

对于任意原始信号x(t)，首先搜寻其所有极值点。以左端极大值为例，从左到右依次标记所有极大值点位置N，N=(N1,N2,…,Nm)，对应的幅值为x(Ni),i=1,2,…,m。首先判断上包络线变化趋势，通过判定最左端三个连续极大值点为“上凸”或“下凹”，确定包络线在端点处是向上或向下发散。计算前两个极大值点间的梯度

(1)

并通过第一个极大值点，确定在这一梯度下的直线y=grade(x-N1)+x(N1)，计算该直线在序列端点处的值y(t1)，若包络线在端点处是向上发散的，则端点值取min{y(t1),x(t1)}；若包络线在端点处是向下发散的，则端点值取max{y(t1),x(t1)}。同样，按照此方法处理上包络线右端点和下包络线左右端点数据，然后进行包络拟合，最后按照LMD算法对信号进行后续处理。需要指出的是，在每次迭代前都要对上下包络线进行拟合，以减小误差。

2仿真研究

为了验证本方法对抑制端点效应的有效性和准确性，采用如下信号进行仿真研究：

x=(1+0.5cos(9pit))cos(200pit+

2cos(10pit))+sin(pit)sin(30pit)

(2)

式中，t=0:0.000 1:3。信号的时域图和分解的PF分量如下图所示，其中图1为未作端点处理的分解结果，图2为采用平行极值延拓方法的分解结果，图3为镜像延拓法的分解结果，图4为本文所提方法的分解结果,图5为各方法残余分量对比图。

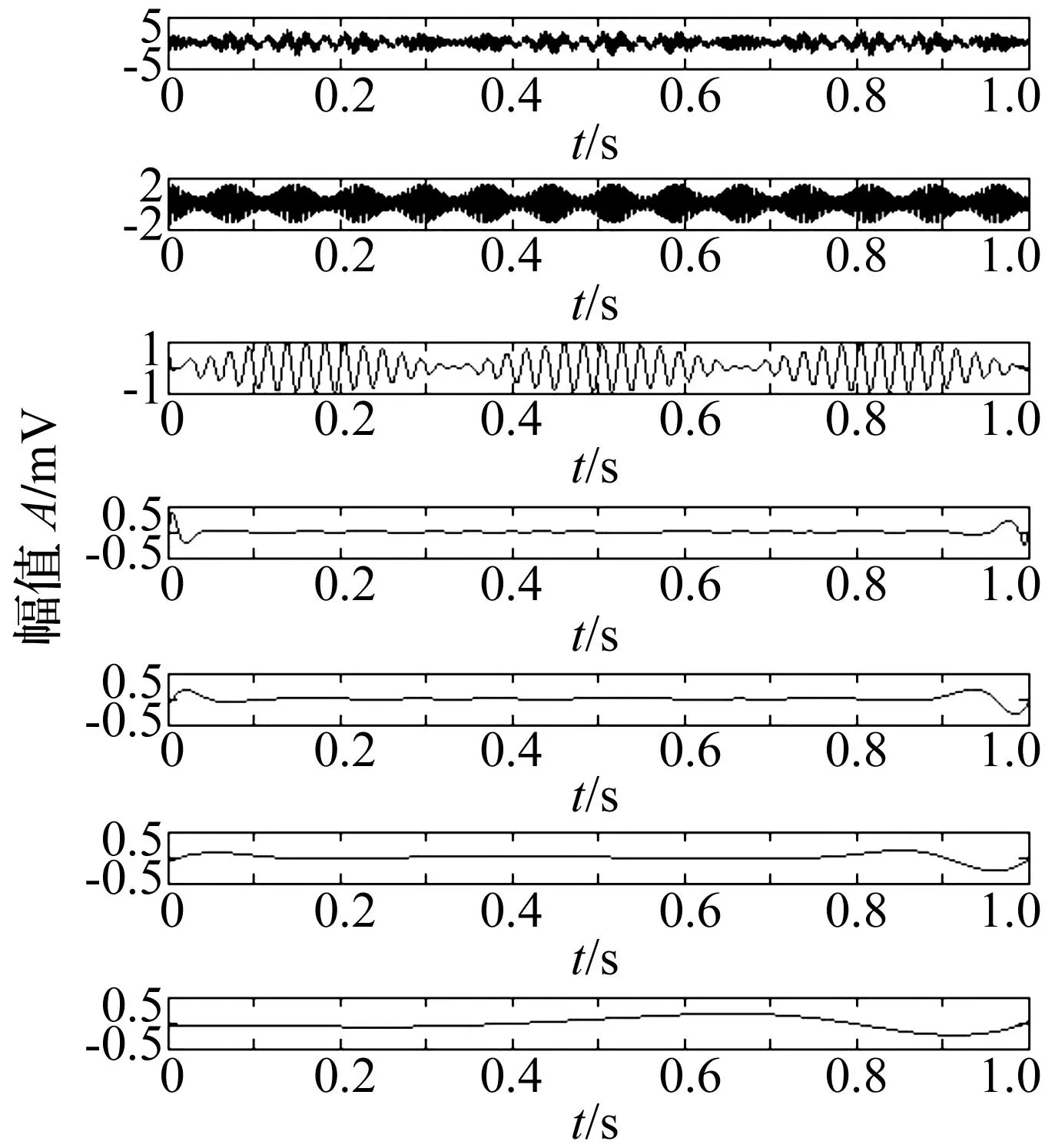
图1　未进行端点处理的分解结果Fig.1 The decomposition from original LMD

图2　采用平行极值延拓的分解结果Fig.2 The decomposition from parallel extending LMD

图3　采用镜像延拓的分解结果Fig.3 The decomposition from mirror extending LMD

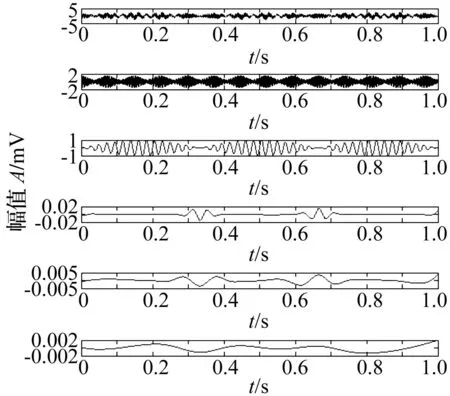
图4　本文所用方法分解结果Fig.4 The decomposition from improved LMD

图5　残余分量对比结果Fig.5 Contrast of residual component

从图1～图5和表1可知，未作端点处理情况下，LMD分解出了五个PF分量和一个残余分量，出现了模态混叠现象，并且残余分量幅值相对经过端点处理的分解结果较大；采用不同端点处理方法的分解结果，提取出了四个PF分量，并且残余分量较小，镜像延拓的分解结果要优于平行极值延拓的分解结果，而本文所用方法的分解结果与镜像延拓的分解结果残余分量在一个数量级，基本相近，略优于镜像延拓分解结果。

表1　残余分量能量

3工程应用实例

本研究通过对滚动轴承故障进行诊断，来验证所提方法工程应用的实用性。实验在多功能高速轴承试验台上进行。实验轴承型号为6010，内径50 mm，外径80 mm，13个直径9 mm滚动体，压力角0°。轴承外圈固定，内圈与转轴相连，转速为6 000 r/min。轴承内圈用线切割制造一处裂纹故障。

由于噪声的污染会对LMD分解结果产生较大影响，导致出现虚假极值，从而使分解结果误差很大，甚至出现模态混叠现象，因此需要对信号中的噪声进行降噪处理。考虑到轴承共振频带未知，传统的滤波方法难以有效提取出轴承共振信号，因此本研究采用SVD降噪方法提出信号中的噪声影响。

在进行SVD分解时，需要合理设置时间延迟τ和嵌入维数m，以尽可能保证重构的矩阵为满秩的，即将信号中各独立成分完全分解出来，不会产生多余成分。本文中采用改进FNN法和互信息法[7-8]确定嵌入维数和时间延迟，时间延迟曲线和嵌入维数曲线如图6和图7所示，可据此确定合理的时间延迟τ=3，嵌入维数m=9。

图6　时间延迟曲线Fig.6 Curve of time delay

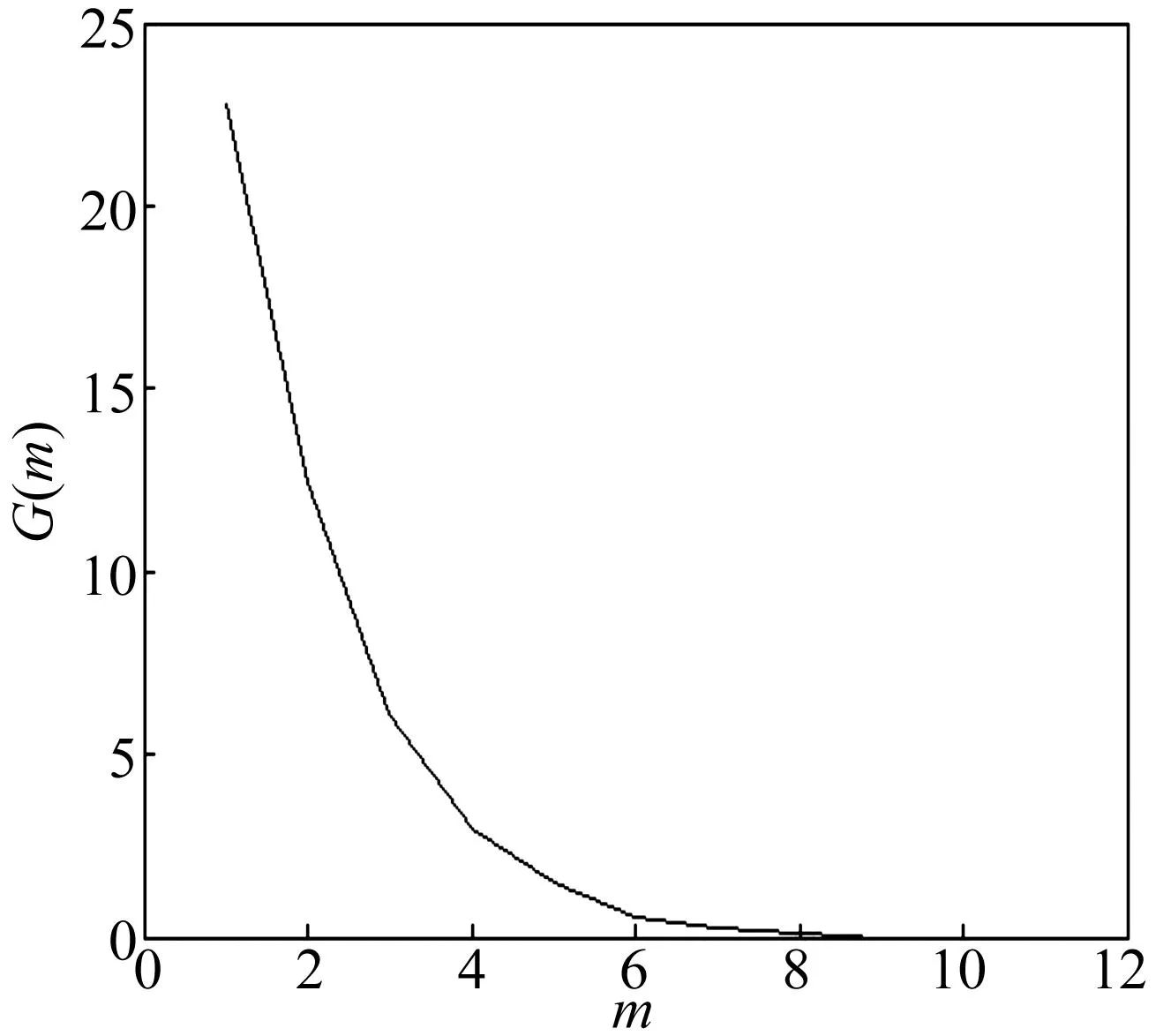
图7　嵌入维数曲线Fig.7 Curve of embedding dimension

经SVD分解，可得到9个奇异值，对应着9个独立的信号分量。奇异值的大小代表着各独立信号在合成信号中能量贡献的大小，因此通常奇异值较大的对应的信号能量贡献较大。由于在实际工程应用中，轴承故障的调制信号的能量往往远小于电机、转轴、齿轮等设备的信号强度，因此应根据实际情况选择合理的奇异值对应的信号。在本研究中，由于转子属于高速转子，因此轴承故障信号极其微弱，故选择最小的奇异值重构信号，并对其进行LMD分解，得到如图8所示的分解结果。分解共得到5个PF分量和一个残余分量。由于振动信号经LMD分解后，冲击信息由于调制而大部分分布在高频PF分量中，并且从分解结果中可见第一和第二个PF分量包含明显的冲击成分，因此选择前两个PF分量重构信号，并进行包络分析，得到如图9所示的幅值谱，其中727 Hz及其倍频谱线明显。

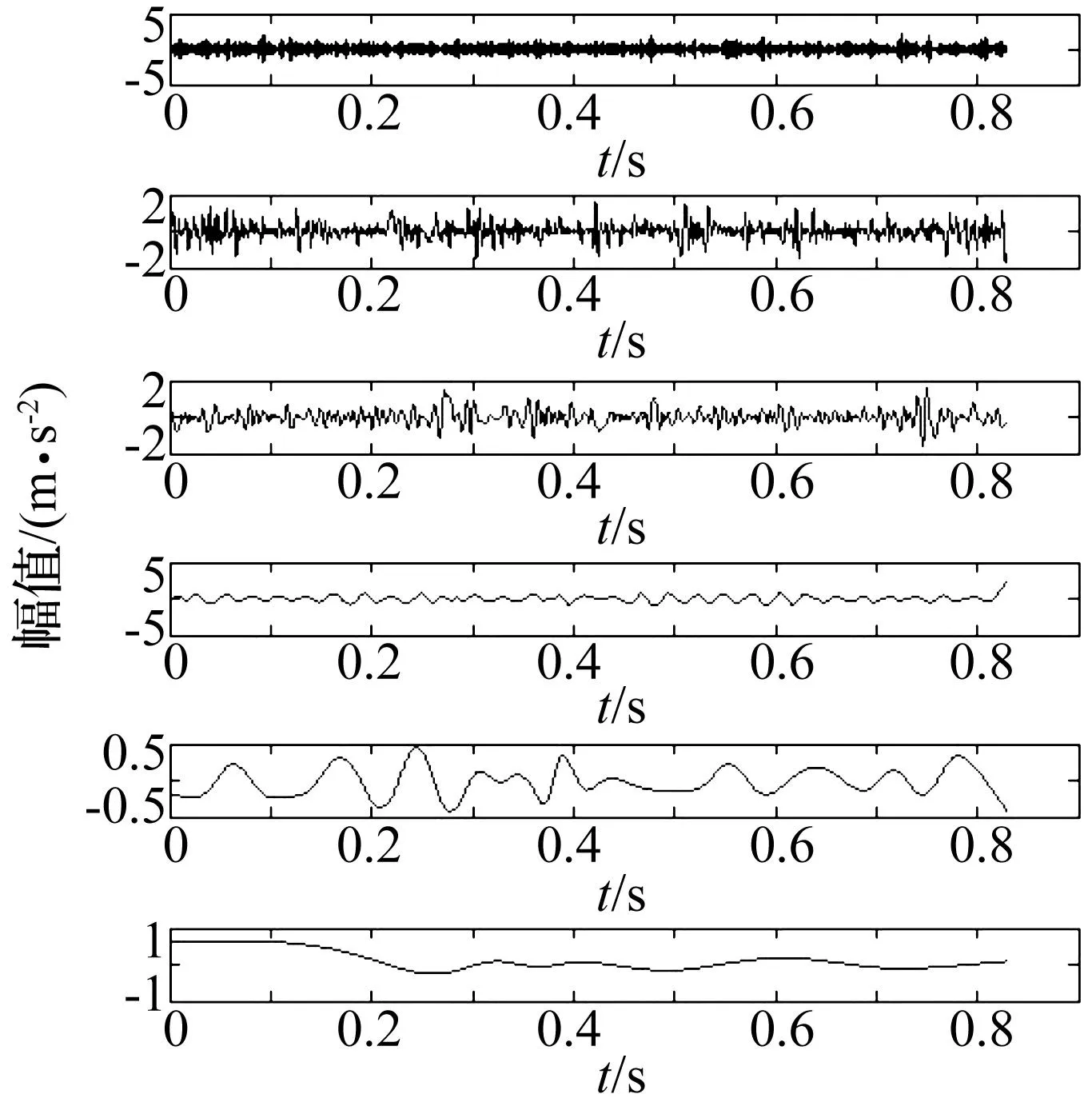
图8　实测信号分解结果Fig.8 The decomposition of measuring vibration signal

实验所用6010轴承在6 000 r/min下内圈故障频率为723.13 Hz，考虑到转速测量等误差，可认为图中727 Hz信号为滚动轴承内圈故障信号。

图9　实测信号包络谱Fig.9 The envelop analysis of the reconstructing signal

4结论

针对LMD方法在处理有限长时间序列时，在分解过程中会产生端点效应的问题，提出了一种基于梯度极值延拓的端点效应抑制方法，该方法充分考虑了时间序列在端点处的变化趋势，使获得的端点处数据更符合数据走势。通过仿真研究表明，该方法可以有效的减小端点效应对LMD分解结果的影响，其效果优于一般端点处理方法；根据滚动轴承故障信号为调制信号的特点，将改进的LMD方法应用于滚动轴承故障诊断，通过实验验证了改进后的LMD分解方法在滚动轴承故障诊断中应用的可行性。

参 考 文 献

[1] 陈龙.基于时延自相关与局部均值分解的齿轮故障诊断方法的研究[D].上海：华东理工大学,2003.

[2] 程军圣,杨怡,杨宇. 基于LMD的能量算子解调机械故障诊断方法[J].振动、测试与诊断,2012,32(6):915-919.

CHENG Jun-sheng, YANG Yi, YANG Yu. Mechanical fault diagnosis of energy operator demodulating approach based on LMD[J].Journal of Vibration, Measurement & Diagnosis,2012,32(6):915-919.

[3] 宋海军,黄传金,刘宏超,等. 基于改进LMD的电能质量扰动检测新方法[J].中国电机工程学报, 2014,34(10):1700-1708.

SONG Hai-jun, HUANG Chuan-jin, LIU Hong-chao. A new power quality disturbance detection method based on the improved LMD[J].Proceedings of the CSEE,2014,34(10):1700-1708.

[4] 杨武. 基于LMD的AR模型在旋转机械故障诊断中的应用[D].大连:大连交通大学,2013.

[5] Jonathan S S.The local mean decomposition method and its application to EEG perception data[J].Journal of the Royal Society Interface, 2005,2(5): 443-454.

[6] 程军圣,罗颂荣,杨斌,等. LMD能量矩和变量预测模型模式识别在轴承故障诊断中的应用[J].振动工程学报,2013,26(5): 751-757.

CHENG Jun-sheng, LUO Song-rong, YANG Bin, et al. LMD energy moment and variable predictive model based class discriminate and their application in intelligent fault diagnosis of roller bearing[J].Journal of Vibration Engineering, 2013,26(5): 751-757.

[7] 刘树勇,朱石坚,俞翔. 确定相空间重构嵌入维数的研究[J].哈尔滨工程大学学报, 2008,29(4):374-380.

LIU Shu-yong, ZHU Shi-jian, YU Xiang. Determinating the embedding dimension in phase space reconstruction[J].Journal of Harbin Engineering University, 2008,29(4):374-380.

[8] Luis A. A nonlinear correlation function for selecting the delay time in dynamic reconstructions[J].Physics Letter A, 1995, 203: 88-94.

An improved LMD algorithm and its application in bearing fault diagnosis

LILin，ZHANGYong-xiang，MINGTing-feng(College of Power Engineering，Naval University of Engineering，Wuhan 430033，China)

Abstract:To decrease the error induced by the boundary effect in the process of LMD, a new method based on the changing grades was introduced.After comparison with other methods by simulation, this method was proved to be more accurate.As the vibration signal of the faulty rolling element bearing was composed by a series of modulating signal, the improved LMD was applied to the fault diagnosis of bearing.This application, in which the SVD was used for noise reduction, was proved to be effective and feasible by experiment.

Key words:LMD; boundary effect; singular value decomposition(SVD); rolling element bearing; fault diagnosis

中图分类号:TP206

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.029

收稿日期：2015-03-09修改稿收到日期：2015-04-16

基金项目：湖北省自然科学基金资助项目

第一作者 李琳 男，博士，讲师，1979年生