六韧带手性蜂窝结构的动力学响应特性研究

张新春， 祝晓燕， 李　娜(华北电力大学 能源动力与机械工程学院，河北 保定　071003)



六韧带手性蜂窝结构的动力学响应特性研究

张新春， 祝晓燕， 李娜(华北电力大学 能源动力与机械工程学院，河北 保定071003)

摘要：利用显式动力有限元ANSYS/LS-DYNA数值研究了六韧带手性蜂窝结构的面内冲击动力学特性。在保证圆环节点半径不变的前提下，通过改变韧带长度和胞元厚度，首先建立了六韧带手性蜂窝的有限元模型，具体讨论了冲击速度和胞元微结构参数对手性蜂窝材料的面内宏/微观变形行为、密实应变、动态平台应力和比能量吸收能力的影响。研究结果表明，随着冲击速度的增加，六韧带手性蜂窝结构表现为3种宏观变形模态：“> <”型模式、“过渡”模式和“I”型模式。在中、低速冲击载荷下，能够明显观察到拉胀材料在轴向压缩时独特的“颈缩”现象，其主要与韧带绕着圆环中心节点的旋转变形有关。通过引入无量纲“动态敏感因子”，还研究了六韧带手性蜂窝材料的面内动态冲击强化效应。

关键词：六韧带手性蜂窝；平台应力；变形模式；动态强化；负泊松比

由于具有优异的动力学响应特性和微结构可设计强等优势，多胞材料/结构常被用作结构防护材料和夹芯填充结构，在众多碰撞及冲击能量吸收技术领域(比如，航空航天、交通运输和汽车等)有着广泛的应用前景[1]。受到冲击载荷作用下，传统多胞材料的宏观变形通常表现为正泊松比特性，很难实现超轻多胞材料的多功能化集成设计以及能量吸收智能化控制的要求。而拉胀多胞材料以其独特的力学和物理性能的优势，并能实现智能化结构设计的要求，吸引了国内外力学家和材料学家的极大兴趣[2-10]。与普通蜂窝相比，拉胀蜂窝材料的微观结构和形变机理明显不同。研究表明，导致蜂窝材料产生负泊松比效应的变形机制主要有两种[2]：内凹机制和旋转机制(见图1)。如何建立胞元微结构与材料宏观动态冲击响应间的关系，并根据实际需求实现能量吸收的智能化自适应设计，也是拉胀蜂窝材料动力学性能研究的前沿课题之一。

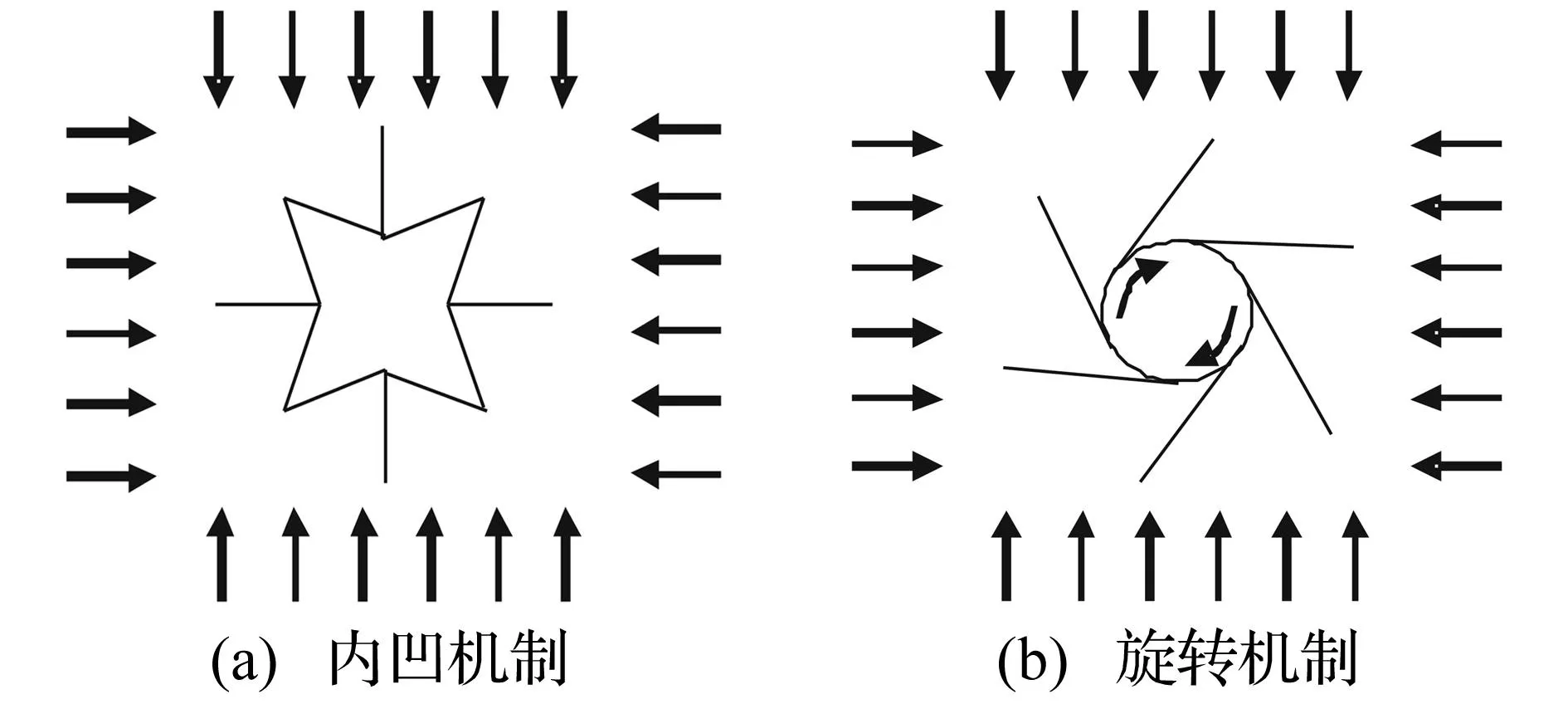
图1　蜂窝材料产生负泊松比行为的两种变形机制Fig.1 Two deformation mechanisms generating an auxetic behavior of the honeycomb

近年来，手性蜂窝结构因其受到压缩荷载作用而表现出独特的变形特性引起了相关学者的关注[5-11]。但要在工程上应用该类新型多胞结构，首先要对其宏/微观力学性能进行充分的研究和认识。关于手性蜂窝结构力学性能的大量研究已经展开。例如，Prall等[5]对六韧带手性蜂窝材料的面内力学性能进行了理论分析和实验研究；Alderson等[6]讨论了几种常见手性蜂窝结构(比如，三韧带、四韧带和六韧带)的弹性模量和泊松比，并进一步阐述了该类结构的变形机制；Lorato等[7]系统分析了不同微结构手性蜂窝的面外线弹性力学性能；Scarpa等[8]研究了六韧带手性蜂窝结构受到均匀平压时的整体和局部线性屈曲特性；Liu等[9]基于连续介质理论对二维手性蜂窝结构的手性效应进行了研究；Haghpanah等[10]讨论了宏观应力状态下三韧带手性蜂窝结构的面内屈曲行为；肖锋等[11]研究了主要设计参数对手性蜂窝橡胶覆盖层水下爆炸抗冲击性能的影响。以上研究发现，胞元微结构对手性蜂窝材料的宏/微观力学性能具有重要影响[6-7]，但目前研究主要集中于模型构建、准静态力学性能预测和应力波传播特性等方面的讨论[5-11]，并没有针对其冲击变形特性和动态冲击强化等其他动力学性能进行展开。需要指出的是，当手性蜂窝结构用作防护冲击材料或能量吸收填充构件时，不可避免的要遭受外来物的冲击，受到冲击载荷下该新型结构的宏/微观动态行为尚缺乏足够的认识。因此，对于手性蜂窝材料动力学响应特性和能量吸收机理的研究显得异常重要。本文以六韧带手性蜂窝为研究对象，对不同冲击速度下手性蜂窝材料的宏/微观变形行为、动态承载能力、密实应变、能量吸收特性和动态冲击强化等动力学响应特性进行了研究，深入剖析胞孔微观结构对手性蜂窝材料宏观动态力学性能影响的内在机理，本研究可进一步为拉胀多胞材料的多目标动力学优化设计提供理论指导。

1模型构建与研究方法

1.1手性蜂窝结构的几何特征

图2为六韧带手性蜂窝结构典型胞元示意图，图中圆环单元称为节点，连接相邻圆环并与其相切的单元称为韧带。根据圆环节点所连接的韧带数目及对称性，可将试件分为六韧带、四韧带同向、四韧带反向、三韧带同向和三韧带反向等手性蜂窝结构[6]。典型胞元的具体几何参数如图2(a)所示，l、R、r、t、θ和φ分别为韧带长度、相邻两圆环节点间的距离、圆环节点半径、胞元壁厚、相邻节点中心连线间的夹角以及中心连线与韧带之间的夹角。对于六韧带手性蜂窝结构，θ=30°，R2=l2+4r2，tanφ=2r/l。该结构胞元具有面内旋转对称的特点，当胞元在面内围绕其中心圆环节点旋转2θ时，可与原结构重合。本文所有的算例中，均保持圆环节点半径r=5 mm不变。

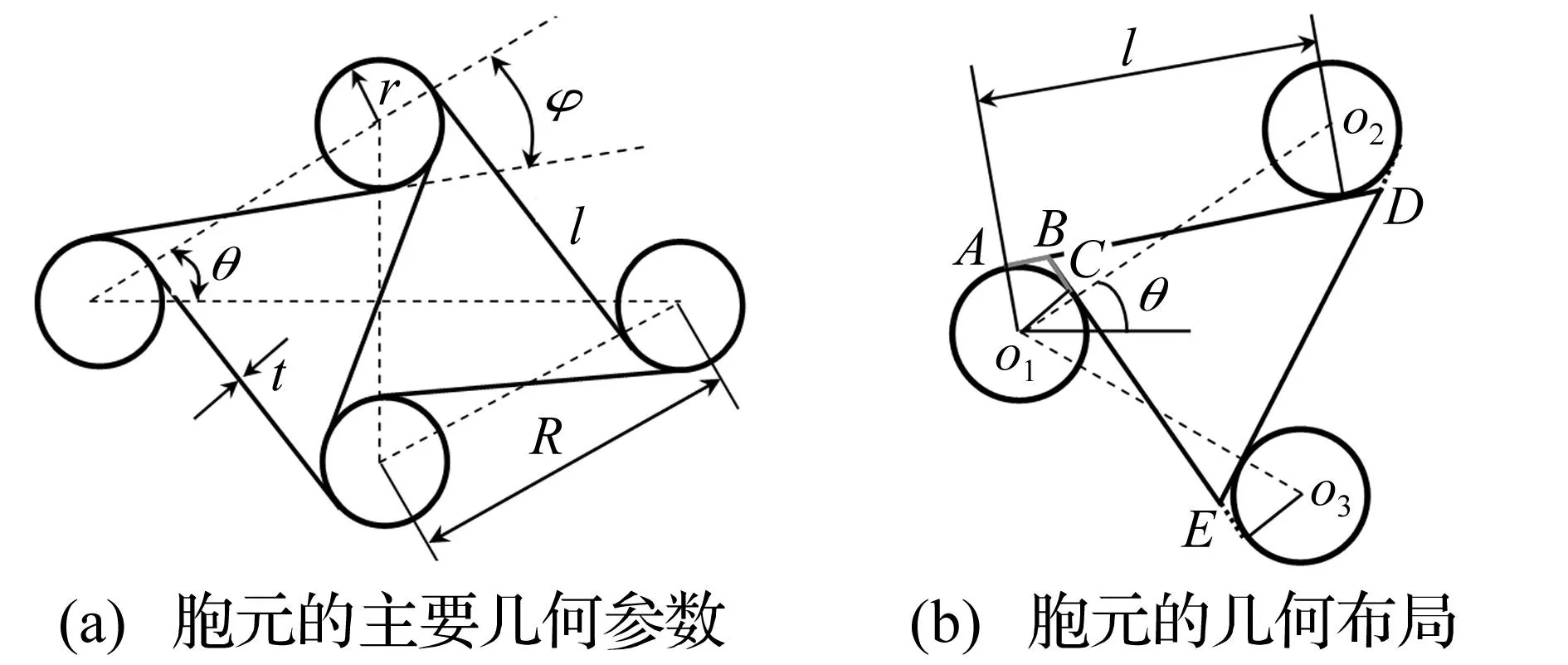
图2　六韧带手性蜂窝结构典型胞元示意图Fig.2 Diagrammatic sketchof typical cell for hexachiral honeycomb

1.2有限元模型

面内冲击载荷下六韧带手性蜂窝结构的计算模型如图3所示。利用显式动力有限元软件ANSYS/LS-DYNA进行面内冲击动力学特性模拟。基体材料为金属铝(Al)，采用弹-塑性随动强化模型。主要材料参数为：杨氏模量Es=69 GPa，屈服应力σys=76 MPa，密度ρs=2 700 kg/m3，泊松比μ=0.3，取强化模量为零。胞壁采用SHELL163壳单元(4节点四边形壳单元)进行离散，韧带单元数目为10，圆环节点单元数目为20，总共有12 120个壳单元。采用全积分Belytschko-Tasy壳单元算法，为了收敛的需要，沿厚度方向定义为5个积分点。对于计算中可能的接触，在刚性板与试件之间设置为面-面自动接触算法(*CONTACT_AUTOMATIC_SURFACE_TO_ SURFACE)，摩擦因数取为0.02；在试件内部各胞元间采用单面自动接触算法(*CONTACT_AUTOMATIC_SINGLE_SURFACE)。边界条件与文献[4]相同，即顶端刚性板以初始速度v沿y方向冲击蜂窝体，底端刚性板固定，试件左右两侧自由。为保证变形的平面应变状态，在模拟过程中，约束所有节点沿z方向位移以防止面外屈曲的发生。

图3　面内冲击作用下六韧带手性蜂窝的计算模型Fig.3 Calculating model of hexachiral honeycomb under in-plane crushing

根据多孔材料(即CMT)理论[12]，手性蜂窝材料的相对密度可由典型胞元的承载面积与其总横断面面积的比值给出。由于总的横断面面积中曲线三角形部分的面积(即ABC部分的面积，见图2(b))与总横断面面积相比可以忽略[8]。所以，总的横断面面积可近似由两个三角形面积(由相连圆环的韧带所构成，见图2(a))加上一个圆环部分的面积构成，即

Atotal=πr2+l2sin2θ

(1)

考虑到每条韧带有两个相邻的胞元所共有，而圆环节点仅与每个胞元有关(见图2)。因此，典型六韧带手性蜂窝晶胞实体部分的面积为

A*=(2πr+3l)t

(2)

因此，六韧带手性蜂窝材料的相对密度可由下式给出，即

(3)

式中：ρ*为六韧带手性蜂窝材料的密度，ρs为基体材料的密度，α和β分别为无量纲参数α=l/r，β=t/r。

1.3平台应力与密实应变

在给定冲击速度下，六韧带手性蜂窝材料的具体动态响应曲线如图4中实线所示。图中显见，面内冲击载荷下六韧带手性蜂窝材料亦表现为三种不同的动态响应阶段：初始线弹性阶段，平台阶段和压缩密实阶段。第二变形阶段中的平台应力(σp)是描述多胞材料动力响应特性的一个非常重要的指标[1,4]，可由下式给出

(4)

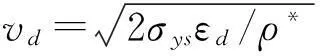
(5)

式中：E为多胞材料的能量吸收效率参数，可定义为在给定名义应变下所吸收的能量与相应名义应力的比值，即

(6)

实际上，多胞材料的能量效率曲线中有很多局部极大值(见图4)。文中定义最后的极大值点(即能量效率曲线开始迅速下降的点)所对应的名义应变为绝对密实化点[4]。

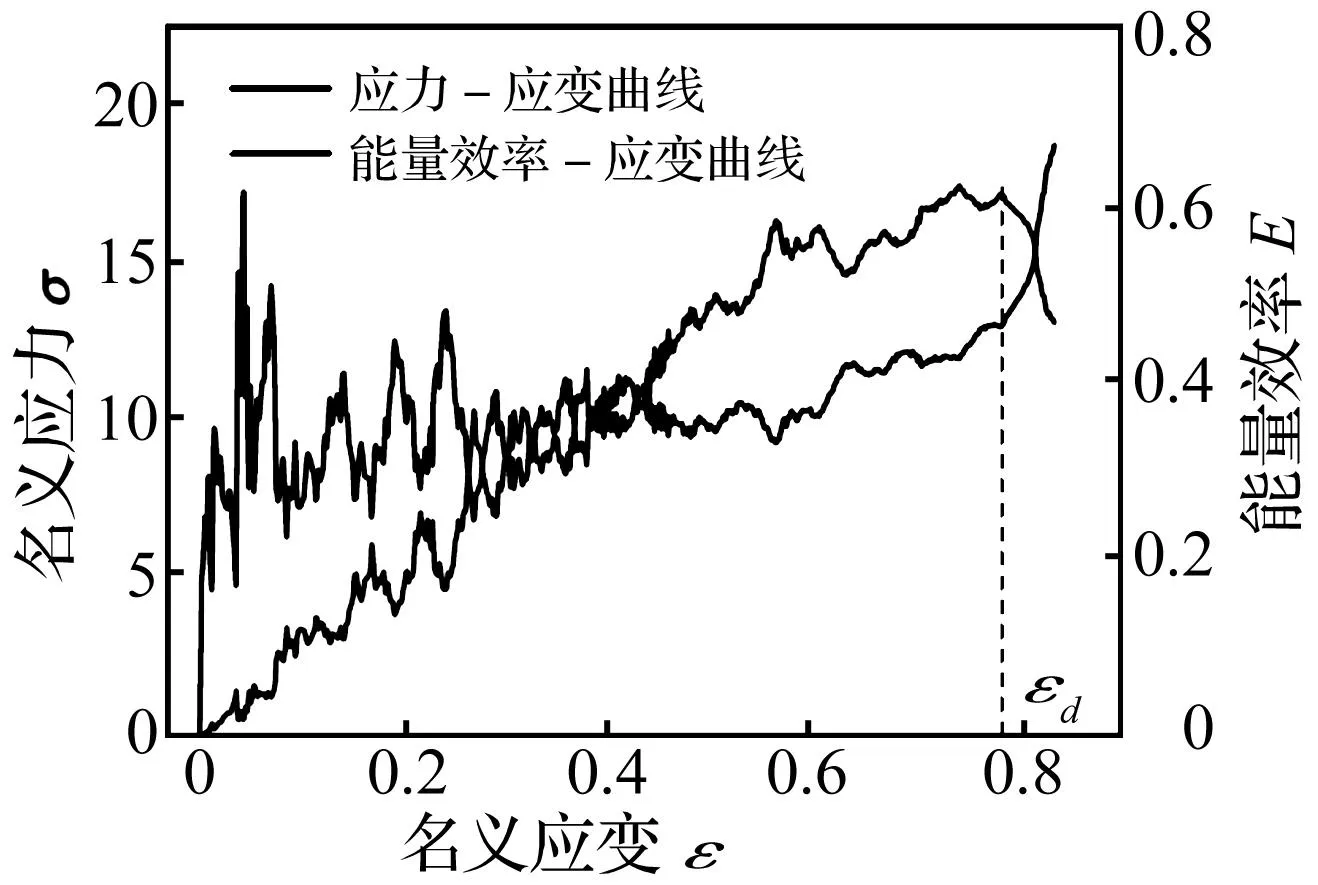
图4　六韧带手性蜂窝材料的动态应力-应变曲线与其对应的能量效率曲线Fig.4 Dynamic nominal stress-strain curve of hexachiral honeycomb and the corresponding energy efficiency curve

为了更好地评估多胞材料的动态平台应力水平，Tan等[13-14]基于率无关、刚性-理想塑性-锁定(R-PP-L)冲击波模型，给出了多胞材料动态平台应力的简单表达式，即

(7)

式中：σp为多胞材料在冲击端的动态平台应力，σ0为多胞材料的准静态平台应力。A为冲击强化参数，可由下式给出

A=Δρρs/εd

(8)

对于规则六边形蜂窝，目前研究相对成熟，Gibson等[12]已给出了其准静态塑性坍塌应力的表达式，即

(9)

结合式(7)～式(9)，正六边形蜂窝材料的动态平台应力可改写为

(10)

为了验证本文数值模拟结果的可靠性，基于式(4)和(10)，图5给出了正六边形蜂窝材料的动态平台应力数值计算结果(式(4))和理论结果(式(10))的比较。在基体材料特性、边界条件和冲击速度完全相同的条件下，数值模拟结果与理论结果吻合较好，从而证明了文中有限元模拟结果的可靠性。在以上分析的基础上，本文对六韧带手性蜂窝材料的面内冲击动力学响应特性进行了数值研究。

图5　不同冲击速度下正六边形蜂窝材料的平台应力有限元模拟结果与理论结果对比Fig.5 Comparison of dynamic plateau stresses for hexagonal honeycombs between FE results and theoretical results under different impact velocities

2数值结果与讨论

2.1变形模式及分类

在面内冲击压溃下，蜂窝材料的动态响应与准静态压缩不同。变形局部化和应力增强是蜂窝材料动态冲击响应的两个典型特征[4,15-16]，而惯性效应则主导蜂窝材料的宏/微观动态变形行为。在冲击载荷作用下，六韧带手性蜂窝在不同名义应变(即试件的竖向压缩位移与试件原始高度的比值)的面内宏观变形如图6所示。与内凹六边形蜂窝[4]、交错排布三角形和四边形蜂窝材料[15]类似，六韧带手性蜂窝材料在中、低速冲击作用下亦表现出“> <”型局部变形模式。当压缩应力超过弹性极限后，各韧带将沿着圆环节点发生顺时针旋转变形，而表现出明显各向同性的宏观变形特征(见图7(a)和7(b))。随着压缩应变的增加，韧带紧紧缠绕在各中心节点上，并逐渐向固定端延伸。继而发生连锁反应，缠绕变形遍及整个试件，直到各圆环节点发生堆积，该现象在低速冲击时相对明显(见图6(a) ～ 6(h))。这种韧带的缠绕与张开正是手性蜂窝结构产生负泊松比行为的变形机制[5]。这一变形阶段称为第一平台阶段，冲击能量主要由韧带的缠绕变形所吸收。与传统蜂窝材料在压缩变形中凸的性质不同[1,12,15-16]，试件在垂直于加载方向上发生明显的“颈缩”现象，而表现出手性蜂窝独特的拉胀变形特性。此时，各韧带紧密缠绕在中心节点上，圆环节点充分接触，其厚度加倍，此时变形更加困难(见图6(c)和6(g))。显然，胞元的缠绕将引起试件的几何钢化效应。随着刚性板压缩位移的增加，圆环节点逐渐被压溃，这一变形阶段称为第二平台阶段，冲击动能主要由圆环节点的压溃变形所吸收。

随着冲击速度的增加(v=70 m/s)，惯性效应增强，韧带的缠绕变形变弱，部分圆环节点被压溃(见图7(c))，变形主要集中于冲击端，“颈缩”现象相对变弱且靠近冲击端(见图6(i) ～ 6(l))。在高速冲击载荷下(v=120 m/s)，惯性效应进一步增强，“颈缩”现象不再发生，靠近冲击端的韧带和圆环节点完全被压溃(见图7(d))，局部变形带表现为一层一层地向固定端传播(见图6(m) ～ 6(p))。这种变形与传统蜂窝材料在高速冲击下的“I”型变形模式一致[1,15]。可见，在低速冲击过程中，六韧带手性蜂窝材料的局部变形主要是由韧带沿着中心节点的缠绕所引起的。局部变形可分为两个阶段：第1阶段为韧带绕着中心节点顺时针缠绕和中心节点的转动，第2阶段为圆环节点胞壁的塑性坍塌。这一阶段的变形模式称之为典型的“> <”型模式(即准静态模式)。在高速冲击载荷下，试件的局部变形主要是由惯性效应引起的，而发生从结构冲击端向固定端渐进的“I”型模式(即动态模式)。在中等冲击速度下，变形模式表现为介于准静态变形模式和高速动态变形模式之间，称之为“过渡”变形模式(见图6(i) ～ 6(l))。

除了冲击速度，韧带长度和胞元厚度亦是影响手性蜂窝结构面内冲击变形模式的重要因素。图8给出了冲击速度v=35 m/s时，无量纲参数α对手性蜂窝材料宏观冲击变形的影响。图中显见，在冲击速度和胞元厚度一定的前提下，韧带长度越小，韧带缠绕变形越明显，其整体“颈缩”现象和几何钢化效应显著增强。随着韧带长度的增加，韧带将在中间位置首先发生折弯，继而绕中心节点缠绕。这种变形导致了手性蜂窝材料“颈缩”现象相对减弱，而发生宏观变形与中等速度冲击下的“过渡”变形模式类似(见图6和8(c))。从图8中可以发现，韧带长度越大，“颈缩”现象越集中于冲击端。数值研究还表明，减少胞壁厚度或增加韧带长度与提高冲击速度具有相同的宏观冲击变形效应。

2.2动态平台应力与能量吸收特性

描述多胞材料冲击能量吸收特性的两个重要技术指标是密实应变和动态平台应力，其与基体材料本身的性能、胞元微结构以及冲击速度等因素有关[1,4,15]。基于能量吸收效率方法，图9给出了六韧带手性蜂窝材料的密实应变与冲击速度间的关系。由图9可知，对于相同的胞元微结构，六韧带手性蜂窝材料的密实应变具有明显冲击速度依赖性，随着冲击速度的增加，手性蜂窝材料的密实应变值也相应增大。但当冲击速度达到或超过冲击波速时，密实应变基本保持不变。在胞壁厚度和冲击速度相同的条件下，手性蜂窝材料的密实应变随着韧带长度的增加而增大，其主要与试件的相对密度有关(见式(3))。

基于有限元模拟结果和式(4)，图10给出了相同胞元厚度但不同韧带长度手性蜂窝材料在冲击端和固定端的动态平台应力与冲击速度间的关系。当胞元厚度和韧带长度为常数时，冲击端的平台应力随冲击速度的增加而增大。在高速冲击作用下，其动态平台应力近似正比于冲击速度的平方。与冲击端动态平台应力不同，固定端试件的平台应力随冲击速度的增加有略微减小的趋势，这主要与手性蜂窝材料的变形模式有关。在高速冲击下，局部变形带集中于冲击端(见图6)。当冲击端的胞元完全被压溃后，固定端的胞元仍处于静止状态。因此，高速冲击下试件在固定端的动态平台应力要低于中、低速冲击的情况。但需要指出的是，对于相同的胞元厚度和冲击速度，其冲击端和固定端的动态平台应力都随韧带长度的增大而减小(见图10和图11)。

图6　不同冲击速度下六韧带手性蜂窝材料的宏观变形模式(α=4)Fig.6 Deformation modes of hexachiral honeycombs under different impact velocities (α=4)

图7　不同冲击速度下六韧带手性蜂窝材料的局部密实变形Fig.7 Local densification deformation of hexachiral honeycombs under different impact velocities

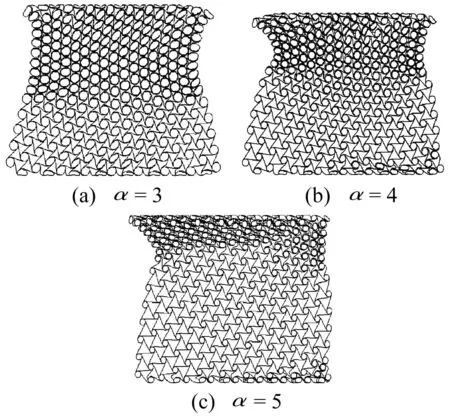
图8　不同韧带长度下六韧带手性蜂窝材料的宏观变形模式Fig.8 Deformation modes of hexachiral honeycombs with different ligament lengths

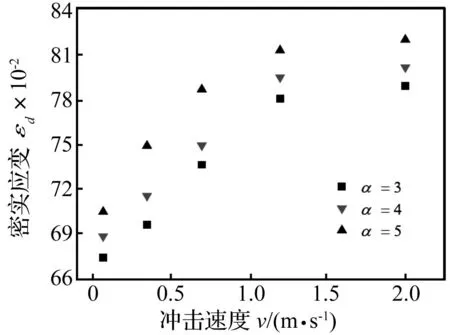
图9　六韧带手性蜂窝材料的密实应变与冲击速度间的关系Fig.9 Variation of densification strain of hexachiral honeycombs with respect to impact velocity

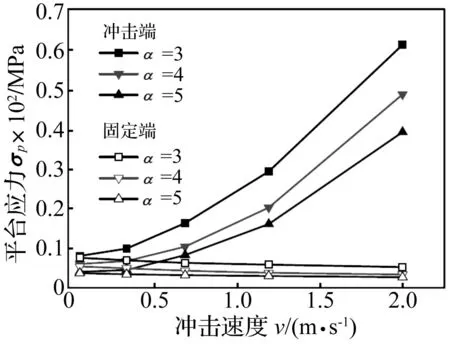
图10　六韧带手性蜂窝材料的平台应力与冲击速度间的关系Fig.10 Variation of plateau stresses of hexachiral honeycombs with respect to impact velocity

图11　相同冲击速度下六韧带手性蜂窝材料冲击端的平台应力与β间的关系(v=35 mm)Fig.11 Variation of plateau stresses in the impacting end for hexachiral honeycombs with respect to β (v=35 mm)

描述蜂窝材料冲击能量吸收特性的另一个非常重要的指标是比能量吸收Em(即单位质量所吸收的能量)，可由下式给出[16]，即

(11)

式中：Δρ为手性蜂窝材料的相对密度，ρs为基体材料的密度。基于式(11)，图12给出了不同冲击速度下六韧带手性蜂窝材料单位质量所吸收的能量。在胞元厚度、冲击速度以及基体材料完全相同的条件下，韧带长度对手性蜂窝材料的能量吸收有重要影响。韧带长度越短，手性蜂窝材料在相同压缩应变下的能量吸收能力越强。一方面，与手性蜂窝材料的变形模式有关。在中、低速冲击下，韧带长度越短，试件的缠绕变形越明显，从而导致几何钢化效应增强(见图8)。另一方面，韧带长度越短，其相对密度越大(见式(3))。随着冲击速度的增加，惯性效应明显增强，手性蜂窝材料表现出更强的能量吸收特性，但韧带长度的影响相对变弱(见图12)。在整个冲击过程中，手性蜂窝材料所吸收的能量大部分由胞元的塑性变形所耗散掉(即韧带的缠绕变形和圆环节点的塑性压溃)，部分转化为动能，还有一小部分则以热能和声能等其他形式耗散掉。与其传统多胞材料的压溃变形不同，手性蜂窝材料在中、低速冲击时通过韧带绕中心节点的缠绕变形来吸收大量的冲击动能，为多胞材料的能量吸收结构的智能化自适应设计提供了新的思路。

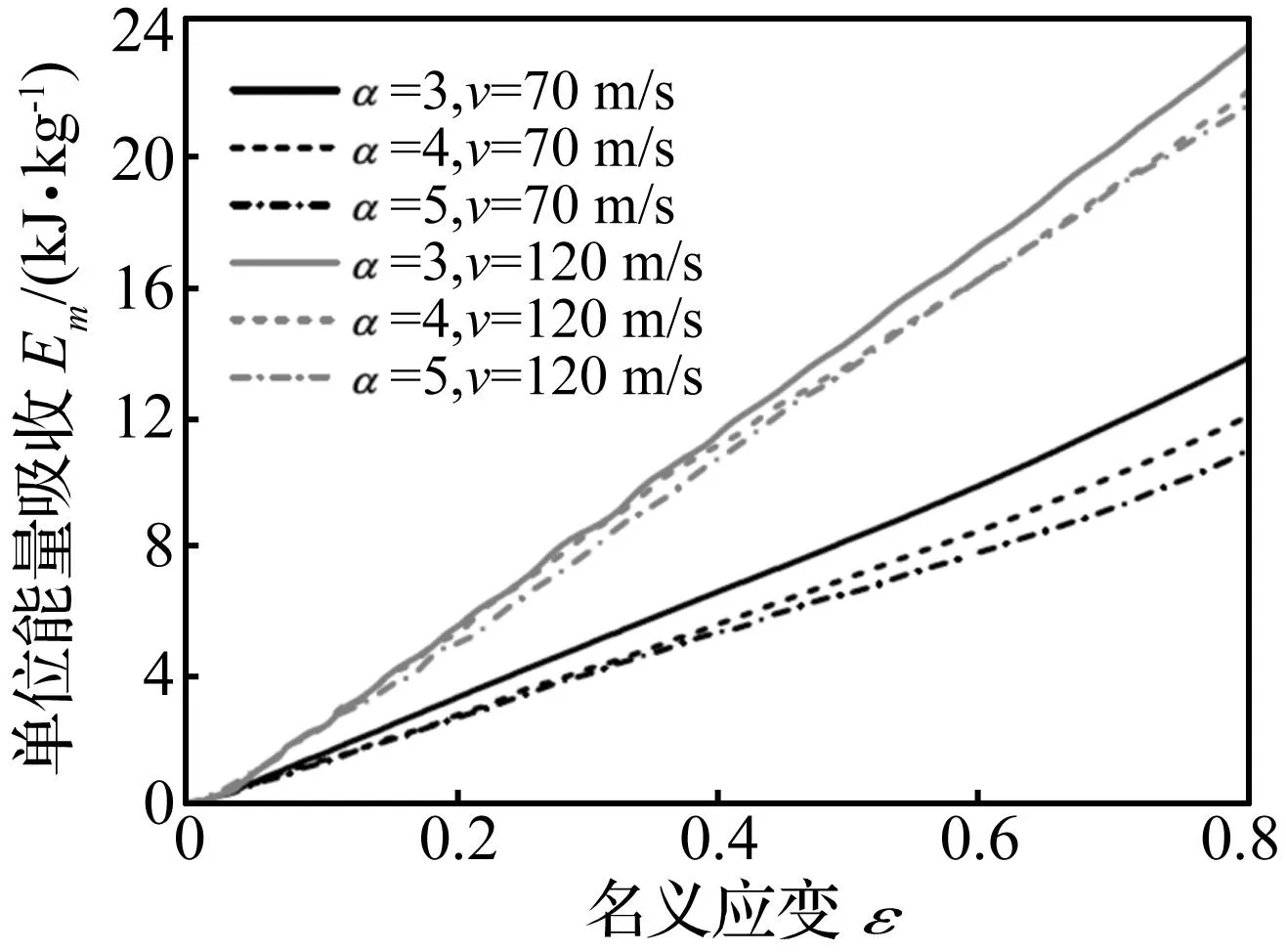
图12　不同冲击速度下六韧带手性蜂窝材料能量吸收比较Fig.12 Comparison of energy absorption ability of hexachiral honeycombs under different impact velocities

2.3动态冲击强化

以上研究结果表明，随着冲击速度的增加，六韧带手性蜂窝材料在冲击端的动态承载能力(见图10)和比能量吸收能力(见图12)均得到强化。这种动态冲击强化主要是由胞元微结构的惯性所引起的。在冲击荷载作用下，蜂窝材料的动态冲击强化现象通常由冲击强化因子γ来评估[17]，即

(12)

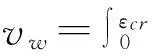
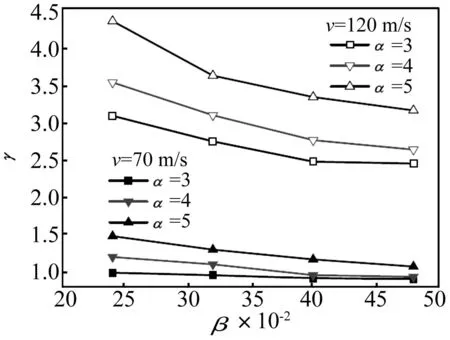
图13　不同冲击速度下六韧带手性蜂窝材料的冲击强化敏感性Fig.13 Dynamic enhancement sensitivity of hexachiral honeycombs under different impact velocities

3结论

基于显式动力有限元方法，本文对六韧带手性蜂窝结构的面内冲击动力学响应特性进行了数值分析。研究结果表明，随着冲击速度的增加，六韧带手性蜂窝结构将依次表现为“> <”型(准静态模式)、“过渡”模式和“I”型(动态模式)3种宏观变形模态。在低速冲击作用下，手性蜂窝结构的各韧带沿着中心圆环节点首先发生顺时针旋转变形，试件表现为明显各向同性的变形特征，进而圆环节点的胞壁发生塑性压溃。试件在垂直于加载方向上发生明显的“颈缩”现象，而表现为“> <”型变形模式。在高速冲击作用下，变形局部化从结构冲击端向固定端渐进发生，表现为“I”型变形模式。在中等冲击速度下，变形模式表现介于准静态和动态变形模式之间的“过渡”模式。在胞壁厚度和冲击速度相同条件下，六韧带手性蜂窝材料冲击端的动态承载能力和比能量吸收能力都随韧带长度的增加而减小，其与胞元的局部变形模式有关。与冲击端平台应力不同，试件固定端的平台应力随着冲击速度的增加相对减小。数值结果还表明，除了冲击速度，六韧带手性蜂窝结构的动态冲击强化因子还敏感于韧带长度和胞壁厚度。

参 考 文 献

[ 1 ] Lu G X, Yu T X.Energy absorption of structures and materials[M].Cambridge: CRC Press, Woodhead Publishing Limited, 2003.

[ 2 ] Prawoto Y.Seeing auxetic materials from the mechanics point of view: a structural review on the negative Poisson’s ratio[J].Computational Materials Science, 2012, 58: 140-153.

[ 3 ] Hou Y, Tai Y H, Lira C, et al.The bending and failure of sandwich structures with auxetic gradient cellular cores[J].Composites Part A: Applied Science and Manufacturing, 2013, 49: 119-131.

[ 4 ] Zhang X C, An L Q, Ding H M, et al.Influence of cell micro-structure on the in-plane dynamic crushing of honeycombs with negative Poisson’s ratio[J].Journal of Sandwich Structures and Materials, 2015, 17(1): 26-55.

[ 5 ] Prall D, Lakes R S.Properties of a chiral honeycomb with a Poisson’s ratio of-1[J].International Journal of Mechanical and Science, 1996, 39(3): 305-314.

[ 6 ] Alderson A, Alderson K L, Attard D, et al.Elastic constants of 3-, 4-and 6-connected chiral and anti-chiral honeycombs subject to uniaxial in-plane loading[J].Composites Science and Technology, 2010, 70(7): 1042-1048.

[ 7 ] Lorato A, Innocenti P, Scarpa F, et al.The transverse elastic properties of chiral honeycombs[J].Composites Science and Technology, 2010, 70(7): 1057-1063.

[ 8 ] Scarpa F, Blain S, Lew T, et al.Elastic buckling of hexagonal chiral cell honeycombs[J].Composites Part A: Applied Science and Manufacturing, 2007, 38(2): 280-289.

[ 9 ] Liu X N, Huang G L, Hu G K.Chiral effect in plane isotropic micropolar elasticity and its application to chiral lattices[J].Journal of the Mechanics and Physics of Solids, 2012, 60(11): 1907-1921.

[10] Haghpanah B, Papadopoulos J, Mousanezhad D, et al.Buckling of regular, chiral and hierarchical honeycombs under a general macroscopic stress state[J].Proceedings of the Royal Society A, 2014, 470(2167): 20130856.

[11] 肖锋, 华宏星,谌勇,等.设计参数对手性蜂窝橡胶覆盖层水下爆炸抗冲击性能的影响[J].振动与冲击,2014,33(1): 56-62.

XIAO Feng, HUA Hong-xing, CHEN Yong, et al.Influences of design parameters on underwater explosion shock resistance of chiral honeycomb rubber cladding[J].Journal of Vibration and Shock, 2014, 33(1): 56-62.

[12] Gibson L J, Ashby M F.Cellular solids: structure and properties[M].Cambridge: Cambridge University Press, 1997.

[13] Tan P J, Reid S R, Harrigan J J, et al.Dynamic compressive strength properties of aluminum foams.Part II—Shock theory and comparison with experimental data and numerical models[J].Journal of the Mechanics and Physics of Solids, 2005, 53(10): 2206-2230.

[14] Reid S R, Peng C.Dynamic uniaxial crushing of wood[J].International Journal of Impact Engineering, 1997,19(5/6): 531-570.

[15] Liu Y, Zhang X C.The influence of cell micro-topology on the in-plane dynamic crushing of honeycombs[J].International Journal of Impact Engineering, 2009, 36(1): 98-109.

[16] Zhang X C, An L Q, Ding H M.Dynamic crushing behavior and energy absorption of honeycombs with density gradient[J].Journal of Sandwich Structures and Materials,2014,16(2):125-147.

[17] Hou B, Zhao H, Pattofatto S, et al.Inertia effects on the progressive crushing of aluminium honeycombs under impact loading[J].International Journal of Solids and Structures, 2012, 49(19/20): 2754-2762.

A study of the dynamic response characteristics of hexagonal chiral honeycombs

ZHANGXin-chun,ZHUXiao-yan,LINa(School of Energy Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China)

Abstract:The in-plane dynamic crushing behaviors of hexagonal chiral (hexachiral) honeycombs were numerically studied by explicit dynamic finite element (EDFE) simulations using ANSYS/LS-DYNA.Assuming that the circular radii are all the same, the FE models of hexachiral honeycombs were first established by the variation of ligament length and cell-wall thickness.The respective influences of the impact velocity and microcell structural parameters on the in-plane macro-/micro-deformation behaviors, densification strains, dynamic plateau stresses and specific energy absorption of chiral honeycombs were discussed.Numerical results show three different types of deformation modes for hexachiral honeycombs with increasing impact velocity: “> <” mode, “transition” mode, and “I” mode.Under low or moderate velocity crushing, hexachiral honeycombs display a particular lateral compression “shrinkage” phenomenon of auxetic materials, which mainly depends on the rotation deformation of the ligament on the central node.By introducing a non-dimensional “dynamic sensitivity index”, the in-plane dynamic enhancement effect of hexachiral honeycombs was also investigated.

Key words:hexachiral honeycomb; plateau stress; deformation modes; dynamic enhancement; negative Poisson’s ratio (NPR)

中图分类号:O347

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.001

收稿日期：2015-02-25修改稿收到日期：2015-04-23

基金项目：国家自然科学基金资助项目(11402089)；河北省自然科学基金资助项目(A2013502120)；中央高校基本科研业务费专项资金资助项目(2014MS117)

第一作者 张新春 男，博士，副教授，1980年4月生

E-mail:xczhang@ncepu.edu.cn