基于CFD/CSD耦合的结构几何非线性静气动弹性数值方法研究

聂雪媛， 黄程德， 杨国伟(中国科学院 力学研究所 流固耦合系统力学重点实验室，北京　100190)



基于CFD/CSD耦合的结构几何非线性静气动弹性数值方法研究

聂雪媛， 黄程德， 杨国伟(中国科学院 力学研究所 流固耦合系统力学重点实验室，北京100190)

摘要：柔性飞行器在气动力作用下会发生大变形，产生结构几何非线性，线性小变形方法难以获得准确的气动弹性分析结果。基于RANs的三维N-S流场控制方程耦合非线性结构静力学方程时域分析方法，用于考虑结构几何非线性的静气动弹性分析。该方法在结构静力学方程求解上采用非线性增量有限元方法进行迭代求解，考虑结构刚度矩阵随结构位形的变化，采用径向基函数方法实现气动/结构界面的数据交换和动网格变形。在建立某型宽体客机复材机翼三维有限元模型的基础上，对其静气动弹性进行了数值仿真，分析了线性结构和考虑结构几何非线性的结构在静气动弹性作用下翼面扭转、展向位移、垂向位移以及升力系数等物理量。算例结果表明，与线性结果相比，非线性结构由于结构几何非线性的影响，在展向和垂向变形上两者存在显著差异。为准确进行柔性结构的气动弹性分析，必须考虑结构几何非线性的影响。

关键词：静气动弹性；结构几何非线性；柔性飞行器

随着对航空工业领域需求的发展，大型运输机，高空长航时无人机得以广泛应用。这类飞行器往往具有大的展弦比结构，并大量使用复合材料，在实现更高的升阻比和更轻的结构质量的同时也增大了结构的柔性，导致结构在气动载荷作用下发生大变形。此时在对这类飞行器进行气动弹性分析时，结构的几何非线性效应不容忽视。

当前对考虑结构几何非线性的气动弹性稳定性分析通常采用气动-结构相耦合的时域数值分析方法，根据气动力计算方法大致可分为两大类，一类为线性气动力耦合梁模型的方法，由Patil等[1-3]提出，采用片条理论或者偶极子格网法计算气动力，研究几何非线性对几何精确梁模型的气动弹性稳定性的影响。杨智春等[4]采用偶极子格网法和梁模型对考虑结构几何非线性效应的颤振特性进行研究，研究结果表明结构几何非线性对其动力学特性影响显著；另一类为非线性气动力耦合非线性梁模型，Smith等[5]采用Euler求解器耦合几何精确梁模型对大展弦比机翼进行了气动弹性分析，Garcia等[6]采用N-S方程计算气动力，对细长机翼进行了非线性气动弹性分析。

已有对考虑结构几何非线性的气动弹性分析的研究中，结构模型几乎都是将三维机翼简化为一直梁模型进行分析，无法体现实际工程应用中的三维模型的真实弹性变形[7]，也无法准确地展现复合材料在结构中的分布和对结构变形的影响。此外，线性气动力模型无法应用于存在强激波或流动分离的流场，无法体现黏性效应。为此，本文提出基于N-S方程耦合三维结构有限元模型的方法用于分析结构几何非线性对气动弹性性能的影响。首先以文献[2]中大展弦比机翼为算例，验证了该方法的准确性，然后以某型号宽体客机的复材机翼作为研究对象，在跨声速流场，分析比较其线性和非线性结构达到静平衡位置后的变形情况。为增强结构的几何非线性效应，本文通过改变来流的攻角来突出线性和非线性结构变形的差异。

1CFD/CSD耦合方法

本文采用气动结构耦合的时域分析方法将流体控制方程和结构动力学方程耦合起来进行求解。这主要是由于流场和结构采用不同的坐标体系描述，难以做到统一求解。非定常气动力的计算采用N-S方程实现，结构动力学方程采用非线性有限元增量法求解。此外，由于气动和结构方程的数值求解都是在离散时间步上进行的，需要相应时刻的结构位移和气动力，这就需要在气动和结构之间建立数据交换，即结构节点位移插值到气动物面网格点；气动物面气动力插值到结构节点。本文采用径向基函数实现界面数据插值和流场动网格变形，考虑结构几何非线性的静气动弹性分析流程如图1所示。

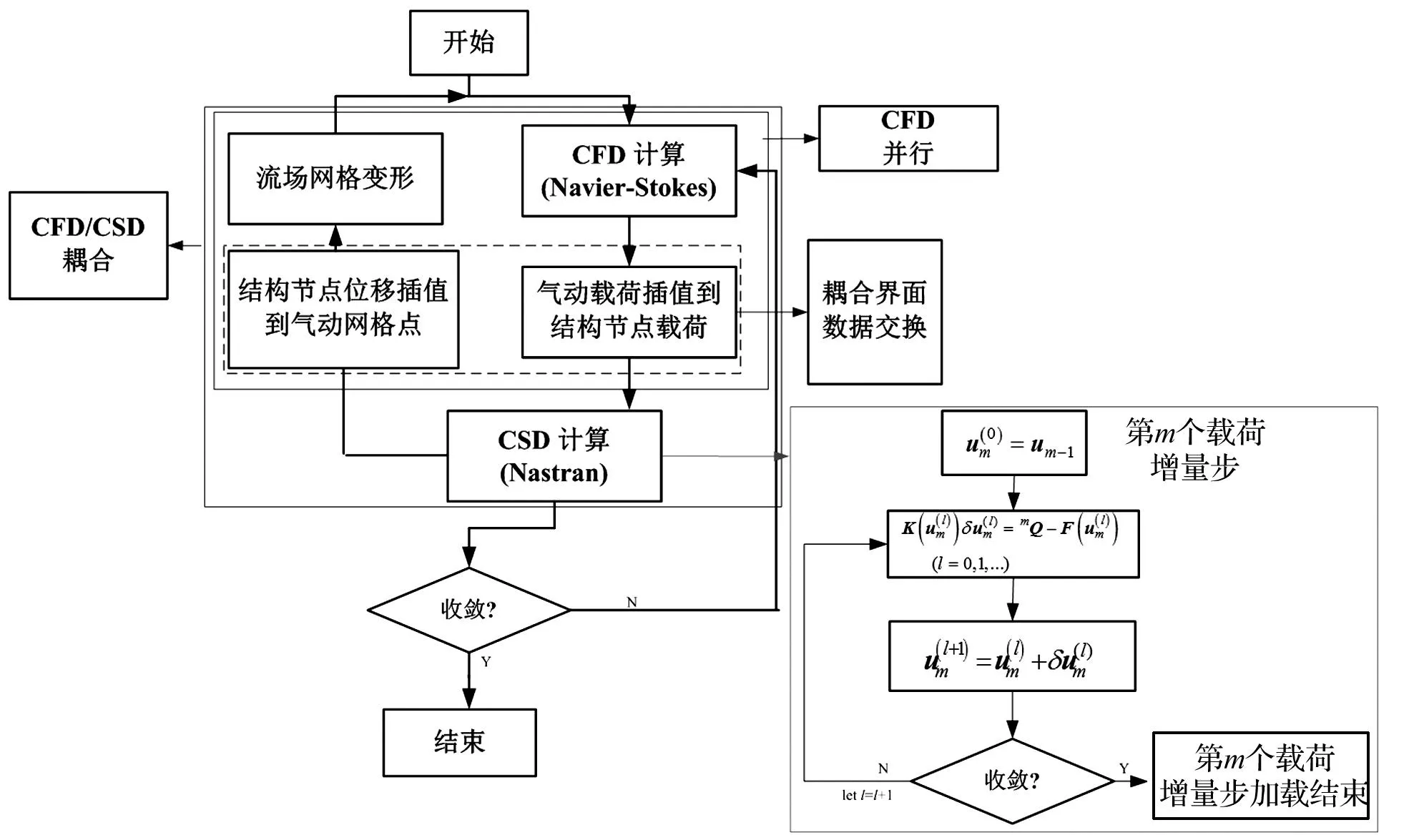
图1　结构几何非线性静气动弹性分析流程Fig.1 Static aeroelastic analysis flow chart for structural geometric nonlinearity

1.1气动控制方程

气动力计算采用基于RANS的三维N-S控制方程， 守恒型的流动方程可表达为，

(1)

式中,Q 为守恒向量，Gc和Gv分别为对流通量和黏性通量，S为控制体V的边界面积，n 代表面的法向量，t代表物理时间。将式(1)按有限体积法进行空间离散可得，

(2)

式中，VI代表第I个控制体单元,NF代表包围第I个单元的所有面数，ΔSm代表第m个表面的法向面积。

N-S方程组空间离散分为无黏项和黏性项。黏性项的离散采用二阶中心差分格式，无黏项是非线性对流的集中体现，因此无黏项离散是空间离散的研究重点。为捕捉激波并避免求解过程中的数值振荡[8]，对无黏项的离散采用Roe格式，即

式中，A为Roe矩阵，上标R，L分别代表相关变量来自单元界面的右边和左边。

对于等式(2)采用二阶三点近似，进行时间离散可得，

(4)

式中，RI称为残差，代表等式(2)的右边项。

为提高时间推进精度，在等式(4)中引入虚拟时间，最终可得到以下时间离散形式，

式中，上标‘*’ 代表虚拟时刻对应的物理量，m为虚拟时间步。本文在虚时间域上采用LU-SGS(Lower-Upper Symmetric Gauss-Seidel) 隐格式对气动方程做隐式时间推进，当子迭代步m→∞时，Q*(m)→Q(n+1)即可求得流场在下一物理时间步的解。

1.2结构静力学求解

结构线性分析认为结构的刚度不会随结构的位形改变，因此对于线性结构静力学方程的解可以通过结构刚度矩阵直接求得。当结构柔度增大产生大变形，引起结构的几何非线性时，结构的刚度矩阵成为随结构位形变化的函数，传统的小变形假设理论不再适用。

在涉及几何非线性问题的有限元方法中，通常采用增量法，将要求解的问题分为若干步，求解每一步的位移，并更新结构刚度，每一步都是以上一步的解作为该步的初始解。由于结构几何非线性效应，使得在建立结构的平衡条件时必须考虑变形后的位形，这就涉及到所参考的平衡位形。在实际分析中，有两种选择[9]，一种是以上一时刻求得的位形作为参考位形，称之为更新拉格朗日格式(Updated Lagrange Formulation, UL)；一种是以时间0的位形作为参考位形，称之为完全拉格朗日格式(Total Lagrange Formulation, TL)。本文采用TL格式对几何非线性问题进行描述，现在假定在时间0到t的所有时间点的解已经求得，当前需要求解t+Δt时刻各物理量，利用虚功原理，结构平衡方程可表示为，

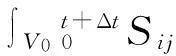
(6)

(7)

(8)

(9)

其中，

将式(7)～式(9)代入式(6)，并对平衡方程进行线性化处理，最终导出用于TL的静力学求解方程为,

(10)

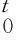
(11)

对式(10)的求解采用增量法，在每一个增量步采用Newton-Raphson迭代算法，由于在每一次迭代中都需要进行刚度矩阵的重新计算，当迭代收敛后，进入到下一个增量，直到增量载荷加载到t+ΔtQ。因此非线性结构与线性结构求解相比要花费更多的计算时间。其具体求解过程可见图1。

1.3数据交换和动网格变形

为给气动控制方程提供运动边界，同时给结构方程提供节点载荷，以实现气动-结构的耦合求解，需要在结构和气动之间进行数据转换，即将结构点位移插值到气动物面网格点，得到气动物面的网格变形，并将气动物面点的气动力变换为结构节点载荷。此外，结构变形也会带动整个空间流场的网格变形。由于该方法插值过程仅需要节点坐标，而无需节点间连接信息，所以数据结构简单，是一种高效的数学插值方法[10]。在本文中采用基于径向基函数[11](RBF)的插值方法用于上述气动-结构之间的界面数据交换和动网格变形，这是一种三维插值方法，其插值公式为，

(12)

式中,s(r)为在空间位置r处需要被估计的函数值，φ为径向基函数，其函数类型表达可参见Wendland[12]，Ns是径向基函数中心点个数，ri是中心点的空间位置，系数γi为插值系数。p(r)是一个可选的多项式，在界面数据交换时，其表达式为p(r)=a0+a1x+a2y+a3z以满足力和力矩平衡的要求；在动网格变形时，该表达式不出现在式(12)中。

RBF实现数据插值的过程可简述如下。设

(13)

ax=(γ1…γNsa0a1a2a3)T

(14)

式中,Ns为用于RBF插值的结构中心点个数，xi,yi,zi(i=1,…,Ns)为中心点坐标。

由式(12)可知，结构节点在x方向上的位移分量可表达为，

usx=Cssax

(15)

式中,Usx=(usx0000)T

根据对插值基函数的研究，本文选取的基函数如式(16)所述。

(16)

通过求解式(15)可得到系数矩阵式(14)，由此可计算出气动物面网格点的位移向量uax为，

uax=Casax

(17)

式中，

Na为气动物面点个数。

根据虚功原理，气动力Fa和结构节点气动力Fs之间满足以下关系

Fs·us=Fa·ua

(18)

利用式(15)和式(17)即可得气动物面气动力到结构节点气动了转换关系为，

(19)

在获得气动物面点位移后，通过贪婪算法[13]选择某些气动物面点用于动网格变形的插值计算，整个插值的过程与上述结构节点到气动物面网格点位移插值相类似。需要指出的是，在动网格变形时，式(13)～式(15)中的后四行数据需要去掉，这是因为网格变形和CFD/CSD 数据交换需要满足的要求是不同的，CFD/CSD 数据变换矩阵需要保证准确的力和力矩平衡准则而包含线性项，而网格变换矩阵为了避免边界网格的移动和非物理力的传递而不需要线性项。另外在基函数的选取上，需要引入紧支半径R，用于控制中心点的作用范围，即基函数形式为

(20)

由于流场网格点数量巨大，将流场网格分块后，采用并行计算实现动网格变形。

2算例与分析

为验证本文中所采用的计算非线性结构静气动弹性算法的正确性，本文首先以诸多文献在研究结构非线性时通常所选取的结构即半展弦比为16∶1的机翼作为研究对象，有关该结构的具体参数见文献[2]。计算在飞行高度20 km，飞行速度25 m/s，攻角为2°时的结构静平衡位置，并与已有文献[5]结果进行了比较，如图2所示。其中面元法和欧拉法为文献[5]计算时采用的方法，CFD为本文计算气动力的方法。

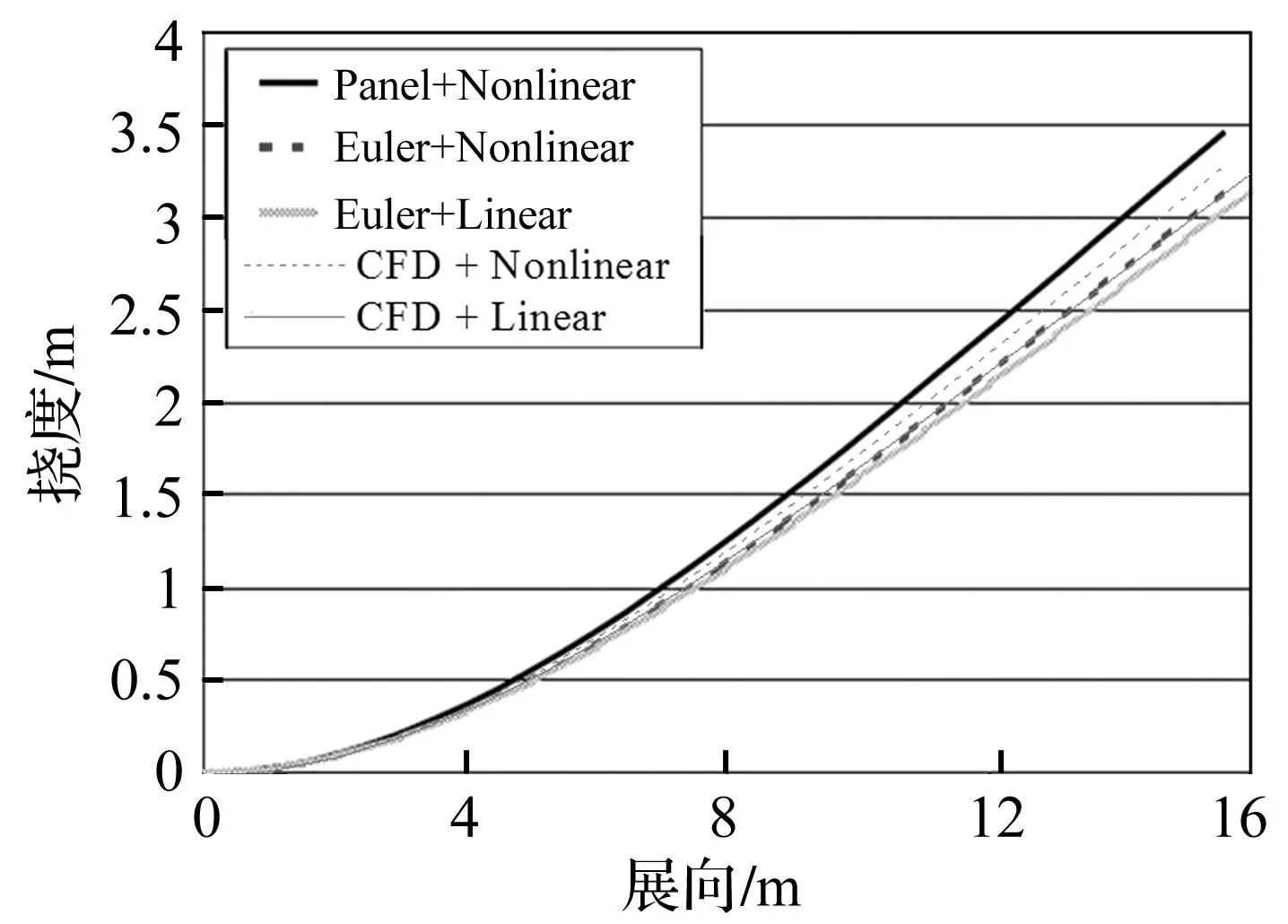
图2　梁结构静气动弹性变形Fig.2 Static aeroelastic deformation of large span ratio beam

从图2可以看出，采用本文所提出方法对非线性结构进行静气动弹性分析，其线性结构和非线性结构的变形规律与文献[5]的研究相似，即非线性结构在垂向上的变形大于线性结构。需要指出的是，由于结构是按照梁结构进行建模，因此在计算线性结构的变形时，轴向是没有位移的，这也是将机翼简单视为梁结构的不足之处。

在对方法进行验证后，本文以某带短舱的宽体客机复材机翼作为研究几何非线性静气动弹性的模型。该机翼展弦比12，梢根比0.2，后掠角30°，翼根弦长约13 m。整个机翼由复合材料按照0°，±45°和90°进行铺层，以增大结构变形时的弯扭耦合效应。在弹性结构有限元分析时认为机身为刚性的，只考虑机翼的弹性变形，其有限元模型如图3所示。流场计算网格采用结构化网格，利用ICEM CFD，以全机半模外形为基础生成O-H型多块对接结构网格，在机翼与机身连接处，采用H型网格，网格在机翼的前后缘方向以及翼根处做了适当加密，以便更好地分辨流场细节。为更好的刻画边界层内的流动，在壁面附近布置了边界层网格，其首层高度为0.05 mm，边界层最大厚度为400 mm。计算网格规模约为1 700万，流场计算网格如图4所示。湍流模型采用两方程涡黏性模型—Wilcoxk-ω模型。

图3　结构有限元模型Fig.3 Structural finite element model

图4　气动表面网格Fig.4 Surface mesh and symmetry plane mesh

该算例的计算条件为：Ma=0.85，Re= 8.264×107，飞行高度11 km，大气密度0.363 92 kg/m3。

通过计算不同来流攻角下结构变形，分析结构几何非线性对静气动弹性特性的影响。分别计算了1°,5°和8°攻角下，线性结构和非线性结构的静平衡位置，图5给出了沿展向在不同攻角下的变形。图6给出了在8°攻角下线性结构和非线性结构在静平衡位置的变形比较。

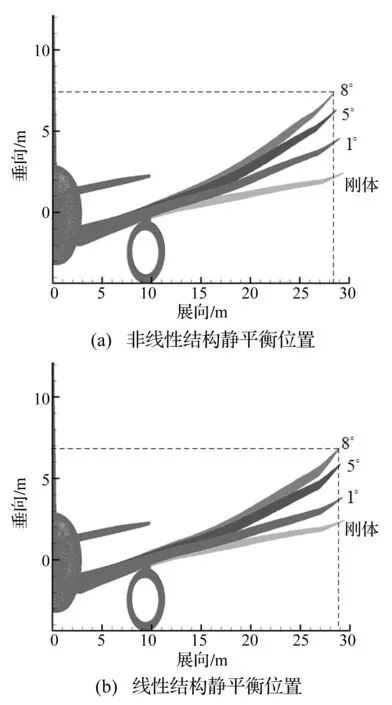
图5　不同攻角下结构沿展向变形比较Fig.5 Spanwise displacement for different attack angle at Mach=0.85

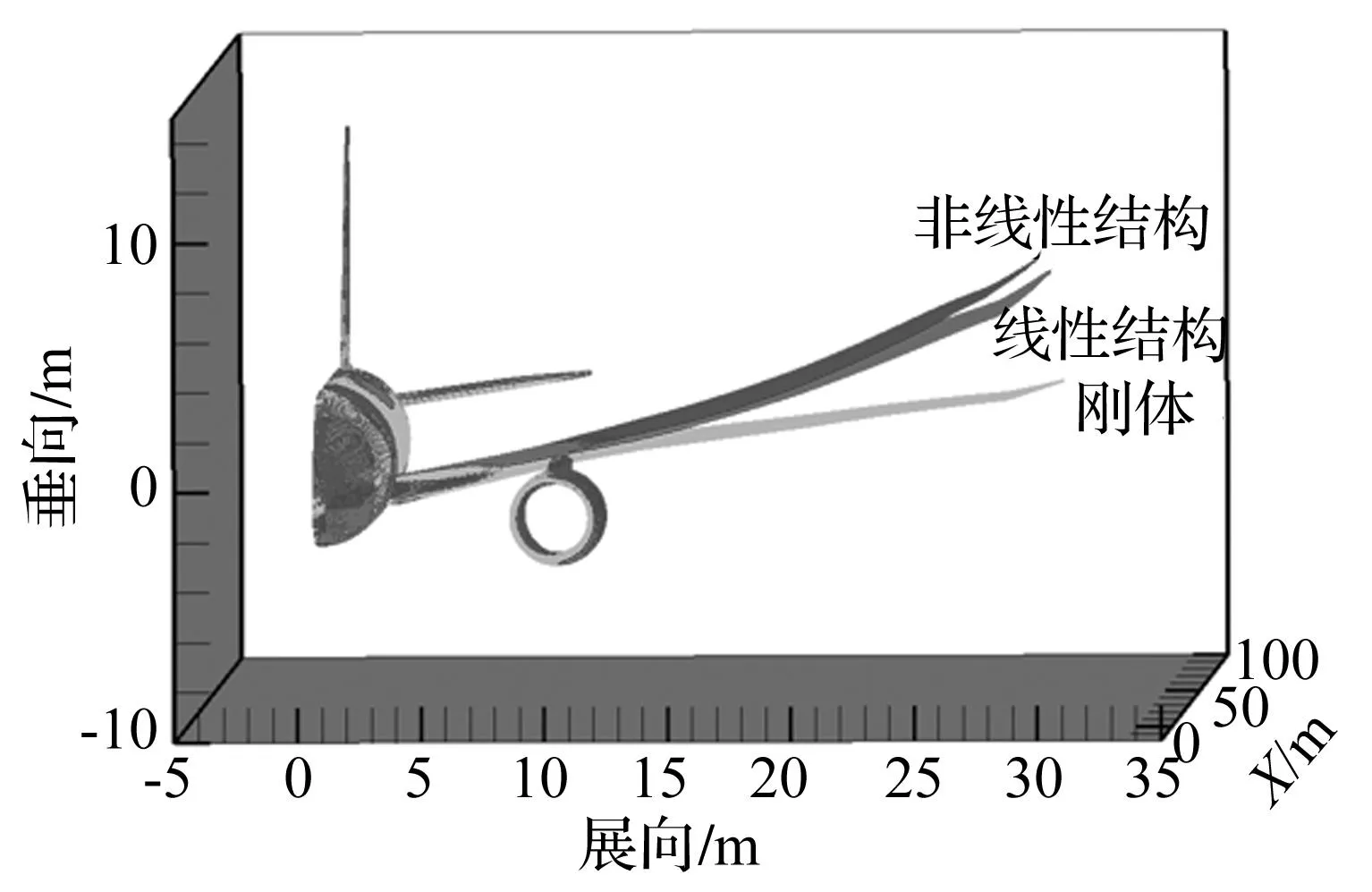
图6　Ma=0.85 8°攻角下结构变形Fig.6 Deformation comparison for linear and nonlinear structure at Mach 0.85 and AOA 8°

从上述两图可看出，与线性结构相比，几何非线性在展向和垂向上的变形都大于线性结构，而且在本计算攻角范围内，随着攻角的增大变形增大。这与Mian[14]中，线性结构在展向没有位移的结论有所不同，分析认为Mian所建立的结构实质为单一的梁结构，而在梁结构的线性计算中，是不考虑展向变形的。

图7给出了在8°攻角时，结构在静平衡位置处，沿展向各剖面的弯矩和扭矩。可以看出非线性结构所受的弯矩大于线性结构，导致非线性结构垂向位移和展向位移大于线性结构。

图7　Ma=0.85 8°攻角下静平衡位置弯扭矩比较Fig.7 Bending and torsion moments comparisons for linear and nonlinear structure at Mach 0.85 and AOA 8°

图8给出了在0.85马赫数下，线性和非线性结构升力系数随攻角的变化，可以看出在本算例中，线性结构在平衡位置的升力小于非线性结构。这可从翼面扭转角来分析，以8°攻角为例，图9给出了沿展向不同剖面的相对扭转角。无论是线性还是非线性结构，由于弹性变形，后掠机翼沿流向各个剖面都会产生负扭转，且该扭转角沿展向增加而增大。在本例中，线性结构在静气动弹性作用下各剖面产生的负扭转角大于非线性结构，导致线性结构飞行攻角小于非线性结构，因此其升力系数小于非线性结构。

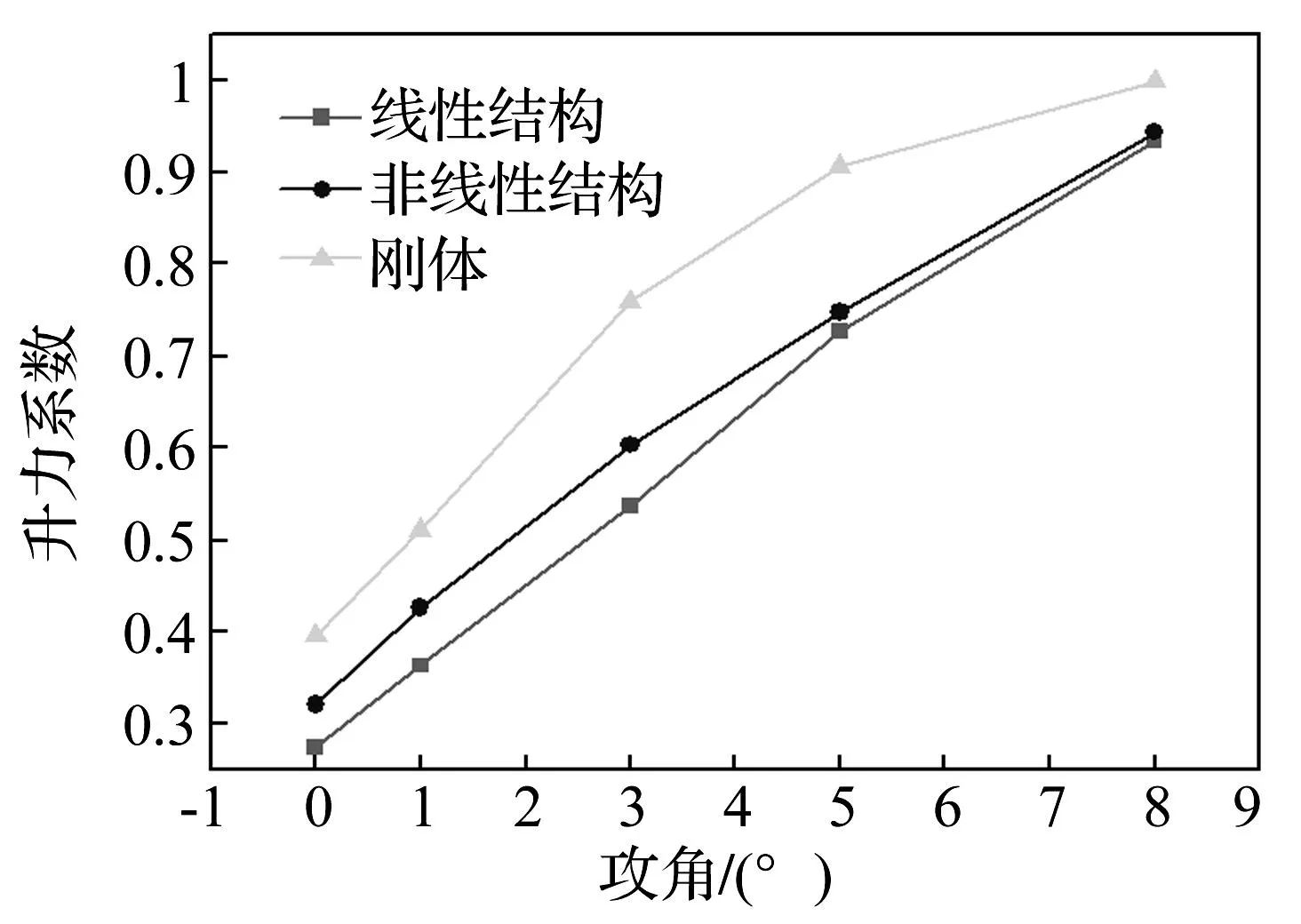
图8　升力系数随攻角变化Fig.8 Lift coefficient curve with different angle of attack at Mach=0.85

图9　沿展向剖面相对扭转角Fig.9 Relative twist angle along spanwise

3结论

本文针对柔性飞行器在气动力作用下呈现出的结构几何非线性特点，采用非线性气动力耦合非线性结构的时域分析方法，对考虑结构几何非线性效应的静气动弹性进行了数值仿真。基于RANs的N-S流场求解器，在虚拟时间歩上采用LU-SGS 方法和 Newton-Raphson方法交替求解非线性气动力和非线性结构变形的紧耦合方式，径向基函数插值方法被用来进行动网格变形和耦合界面数据插值。运用所发展的算法对已有文献算例进行了方法验证，然后对某宽体客机复材机翼的静气动弹性开展研究，比较了线性和非线性结构的静气动弹性特性。针对本文算例，可以得到以下结论:

(1) 无论是线性还是非线性结构，对于后掠角机翼，由于弹性变形的影响，机翼沿流向各个剖面会产生负的扭转角，且随着展向的增大，各剖面扭转角增大，机翼飞行攻角减小；

(2) 非线性结构因变形产生的各剖面负扭转角小于线性结构，因此线性结构在静平衡位置时的升力小于非线性结构；

(3) 采用CFD与结构耦合的方法进行静气动弹性分析，在结构达到平衡位置时，线性结构在展向上有变形；非线性结构的展向位移大于线性结构；在相同展向站位处，非线性结构的垂向变形大于线性结构。

参 考 文 献

[ 1 ] Patil M J, Hodges D H. Limit cycle oscillations in high-aspect-ratio Wings[C]//AIAA-1099-1464,April12-15,1999,St.Louis,Mo,USA.

[ 2 ] Patil M J, Hodges D H. On the importance of aerodynamic and structural nonlinearities in aeroelastic behavior of high-aspect-ratio wings[J]. Journal of Fluids and Structures,2014,19(7):905-915.

[ 3 ] Patil M J, Hodges D H, Cesnik C E S. Characterizing the effects of geometrical nonlinearities on aeroelastic behavior of high-aspect-ratio wings[C]// International Forum on Aeroelasticity and Structural Dynamics, June 22-25,1999,Williamsburg, VA,USA.

[ 4 ] 杨智春, 张惠，谷迎松,等.考虑几何非线性效应的大展弦比机翼气动弹性分析[J].振动与冲击，2014,33(16):72-75.

YANG Zhi-chun, ZHANG Hui, GU Ying-song, et al. Aeroelastic analysis of the high aspect ratio wing considering the geometric nonlinearity[J]. Journal of Vibration and Shock, 2014,33(16):72-75.

[ 5 ] Simth M J, Patil M J,Hodges D H. CFD-based analysis of nonlinear aeroelastic behavior of high-aspect ratio wing [C]// AIAA 2001-1582,April 16-19,2001,Seattle, WA USA.

[ 6 ] Garcia J A,Guruswamy G P. Aeroelastic analysis of transonic wings using Navier-Stokes equations and a nonlinear beam finite element model[C]//AIAA 1999-1215,April 12-15,1999, St. Louis,MO,USA.

[ 7 ] Palacios R,Cesnik C E S. Static nonlinear aeroelasticity of flexible slender wings in compressible flow[C]//AIAA 2005-1945,April 18-21,2005,Austin,TX,USA.

[ 8 ] Roe P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics,1981,43:357-372.

[ 9 ] 王勖成.有限单元法[M].北京：清华大学出版社，2002.

[10] 张伟伟，高传强，叶正寅. 气动弹性计算中网格变形方法研究进展[J]. 航空学报,2014(35):303-319.

ZHANG Wei-wei,GAO Chuan-qiang,YE Zheng-yin. Research progress on mesh deformation method in computational aeroelasticity[J]. Acta Aeronautica et Astronautica Sinica,2014(35):303-319.

[11] Michler A K. Aircraft control surface deflection using RBF-based mesh deformation[J]. International Journal for Numerical Methods in Engineering,2001,88:996-1007.

[12] Beckert A, Wendland H. Multivariate interpolation for fluid-structure interaction problems using radial basis functions[J]. Aerospace Science and Technology,2001,5(2):125-134.

[13] Rendall T C S,Allen C B. Reduced surface point selection options for efficient mesh deformation using radial basis functions[J]. Journal of Computational Physics,2010,229: 2810-2820.

[14] Mian H H, Wang Gang, Ye Zheng-yin. Numerical investigation of structural geometric nonlinearity effect in high-aspect-ratio wing using CFD/CSD coupled approach[J]. Journal of Fluids and Structures, 2014,49:186-201.

Numerical analysis for aeroelastic with structural geometrical nonlinearity using a CFD/CSD-coupled method

NIEXue-yuan,HUANGCheng-de，YANGGuo-wei(Key Laboratory for Mechanics in Fluid Solid Coupling Systems of Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China)

Abstract:Flexible aircrafts tend to undergo large deformations under aerodynamic forces.As a result, structural geometric nonlinearity occurs.The linear small-deformation theory cannot provide accurate results for analyzing static aeroelasticity.Fluid structure-coupling method based on three-dimensional RANs, Navier-Stokes equations and nonlinear static equation is used for static aeroelastic analysis with structural geometric nonlinearity.The mentioned approach adopts the nonlinear incremental finite-element method to solve nonlinear static equations with assembled structure stiffness matrixes.Moreover, RBF method is used for data interpolation and mesh deformation.Based on the multi-material wing finite-element model, the numerical simulations were made to analyze the static aeroelastic behavior.Comparisons of twist angles, vertical displacements, spanwise displacements and life coefficients between linear and nonlinear structures were made.The results show that geometric nonlinearity cannot be neglected for predicting accurate static aeroelastic behavior for large, flexible airplanes.

Key words:static aeroelastic analysis; geometric nonlinearity; flexible aircrafts

中图分类号:V211

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.008

通信作者杨国伟 男，博士，研究员，1967年生

收稿日期：2015-07-28修改稿收到日期：2015-09-24

基金项目：国家高技术研究发展计划(863计划)(2014AA110501)

第一作者 聂雪媛 女，博士，助理研究员，1978年生

E-mail:gwyang@imech.ac.cn