地震模拟振动台多向扩展系统

程麦理， 李青宁， 吴　多， 毕研超， 苗如松(西安建筑科技大学 土木工程学院，西安　710055)



地震模拟振动台多向扩展系统

程麦理， 李青宁， 吴多， 毕研超， 苗如松(西安建筑科技大学 土木工程学院，西安710055)

摘要：为利用单振动台实现大跨度空间结构多维多点激励的振动台试验研究，提出地震模拟振动台改向扩展系统概念。结合曲杆机构改变地震波传递方向的特性，对地震模拟振动台扩展系统进行结构动力分析。根据多点激励理论，考虑上部结构惯性力对子台的作用，推导出子台等效质量的计算公式。在谐波荷载作用下，给出多向扩展系统动力响应的解析式。研究表明，多向扩展系统能有效改变地震波的峰值加速度、相位和传递方向，是一种利用单振动台实现大跨结构多维多点激励试验研究的有效方法。算例结果验证了该理论的正确性，为振动台多向扩展系统的研制提供理论依据。

关键词：振动台；扩展系统；多维多点；曲杆机构

为研究空间大跨结构的整体抗震性能，可通过地震模拟振动台试验最大程度真实再现结构在地震作用下的动力工作行为，振动台试验是研究和评价结构抗震性能的最有效方法[1]。

由于空间大跨结构跨越能力强，可获得较大的利用空间，在工程实践中得到了广泛的应用。然而正是由于该类结构空间范围大，使得地震过程中在建筑各支承点接收的地震激励有差异[2-6]。例如：在建筑场地局部地形效应引起的结构局部支承地震动幅值和相位变化；地震波传递方向与地裂缝呈一定夹角时，地震波穿越地裂缝将会引起地震波的传播方向改变和频谱改变；平面不规则的大跨曲线长桥在各桥墩墩底输入径向或切向的地震动等问题。如果在分析该类结构的地震动响应时,仍按照传统的单向地震激励分析方法,分析模拟该类结构的地震动力行为及抗震性能就显得与实际不符，不能合理反映结构真实的动力工作状态。为研究工程结构在多维多点地震激励下的动力工作性能，日本首先研制成功4个3m×2m的地震模拟振动台台阵系统[7]，很好的实现大跨结构的非一致地震激励研究。但由于台阵系统造价高昂，试验过程及后期维护成本高，因而可尝试对单个振动台进行设计改造，以期实现多维多点地震激励方式，最大程度降低试验成本。

本文利用曲杆机构的改向特性，提出对单个单向地震模拟振动台进行多向扩展，突破单向单振动台的一致激励方式，实现多维多点激励试验研究。将地震模拟振动台系统分为母台(原振动台)和子台(扩展台)及曲杆改向装置。为方便研究，将母台、子台均简化为质点，考虑上部结构惯性力对子台的动力作用，推导给出子台等效质量的计算公式；考虑曲杆弯曲刚度及多维输入时结构模型内刚度影响，推导求解系统振动方程。通过算例分析子台动力响应稳态解与母台间动力输入的幅值和相位差异。算例对本文理论进行了验证，结果表明：本文方法可行，可为地震模拟振动台多向扩展提供指导。

1振动台多向扩展系统理论

为实现单向单振动台对结构模型的多维多点激励动力试验，可利用曲杆改向转置改变地震动激励的输入方向。假定：忽略曲杆转动引起台面的径向位移，杆件分析采用集中质量模型，等效质量根据实际结构模型确定。根据地震模拟振动台改向扩展系统分析简化原则，图1为扩展系统分析简图。

图1(a)中，导向轨道在试验中应可靠固定在地基上，使得子台沿其轨道方向运动，子台运动通过曲杆装置传递母台动力输入。图1(b)中，O点为固定转动铰，在进行试验过程中该点应与地基可靠固定，其为曲杆装置改变方向提供平面内支反力；角度θ为子台改向的转向角；A点为曲杆与母台的连接点，用mA表示母台等效质量；点B为曲杆与扩展子台连接点，等效质量为mB；子台处设置的弹簧刚度k为结构试验模型的等效内刚度，可根据具体的试验结构模型计算确定。

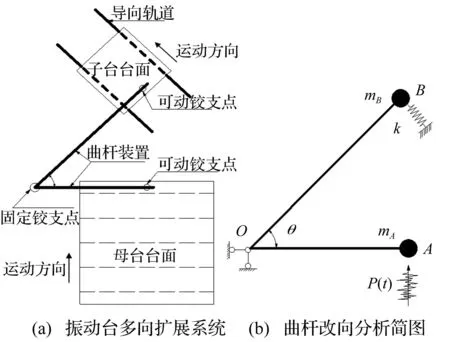
图1　改向扩展系统Fig.1 Redirection extended system

1.1静力分析

为确保曲杆改向系统在试验过程中可靠工作，系统支点O处的支反力应根据静力学基本原理计算求得，计算简图如图2所示。图中l1、l2分别为与母台和子台连接杆的长度。

图2　曲杆改向系统静力分析简图Fig.2 Curved bar redirection system static analysis diagram

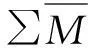
(1)

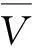
(2)

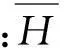
1.2动力分析

1.2.1系统动力特性分析

利用柔度法求解结构动力特性。式(3)给出了扩展系统的固有频率

(3)

式中ω1、ω2分别为曲杆扩展系统的一阶、二阶自振频率；I1、I2分别为与母台和子台连接曲杆的抗弯刚度。系统刚度矩阵为

(4)

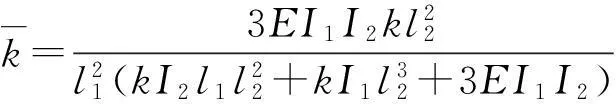
1.2.2系统动力响应分析

假定在母台处输入位移荷载vA(t)，子台绝对位移分解为静力响应位移vba(t)和动力响应位移vb(t)，即vB(t)=vba(t)+vb(t)。根据达朗贝尔原理，图3给出子台质点动力平衡[8]分析简图。

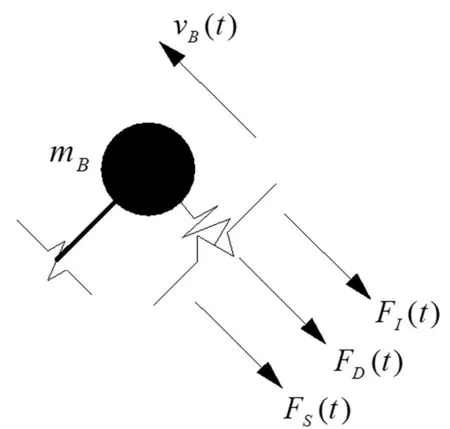
图3　子台质点动平衡Fig.3 Dynamic balance of sub-sets

(5)

式中：c为曲杆系统阻尼系数。

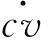
根据曲杆改向扩展系统静力分析，子、母台间静位移传递关系为

(6)

将式(6)代入式(5)可知

(7)

式(7)即为振动台多向扩展系统的振动方程。

2子台等效质量

在地震模拟振动台多向扩展系统工作过程中，由于子台受上部结构模型振动的影响，使得子台受上部结构惯性力的作用。为考虑该影响，引入拟静力模态矩阵概念，合理确定上部结构对子台动力作用及对子台等效质量的贡献。

根据结构多点激励理论[9-10]，结构不同支承点处输入不同地震动载荷时，结构的振动方程为

(8)

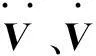
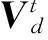
(9)

将式(9)代入式(8)的第一项，忽略所有动力项，非支座节点的拟静力位移可表示为

(10)

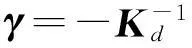
展开式(8)第二项，并忽略所有动力项

(11)

将式(10)变换后代入式(11)可知

(12)

Qe=λQd

(13)

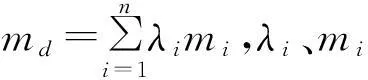
(14)

式中：mb为子台台面质量；n为上部结构集中质量点数。

3振动方程求解

根据傅里叶积分变换原理，任意周期地震波荷载均可由若干条谐振波荷载叠加而成[8]，因而对在谐波荷载作用下的振动台多向扩展系统振动方程求解显得十分必要。

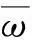
vB(t)=(AcosωDt+BsinωDt)exp(-ξωt)+

(15)

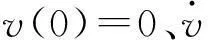
(16)

对式(16)整理可知

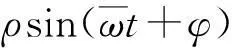
(17)

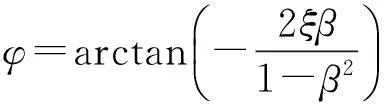
(18)

通过式(17)及式(18)可知，子台的动力输出与母台动力输入存在差异。子、母台的相位差φ和动力放大系数D为两个关键传递参数，在对结构进行多点多向地震激励研究时往往需要考虑结构不同支承点间地震荷载的差异，相位滞后、幅值增减均是结构多点多向激励研究的热点问题。行波效应可较好的用相位滞后来表征，动力放大系数D可模拟局部场地效应对地震波的放大或缩小效应。可根据试验研究的侧重点对该两关键参数进行设计利用，通过曲杆杆件刚度及系统阻尼、质量分布进行调节控制。

4算例

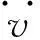
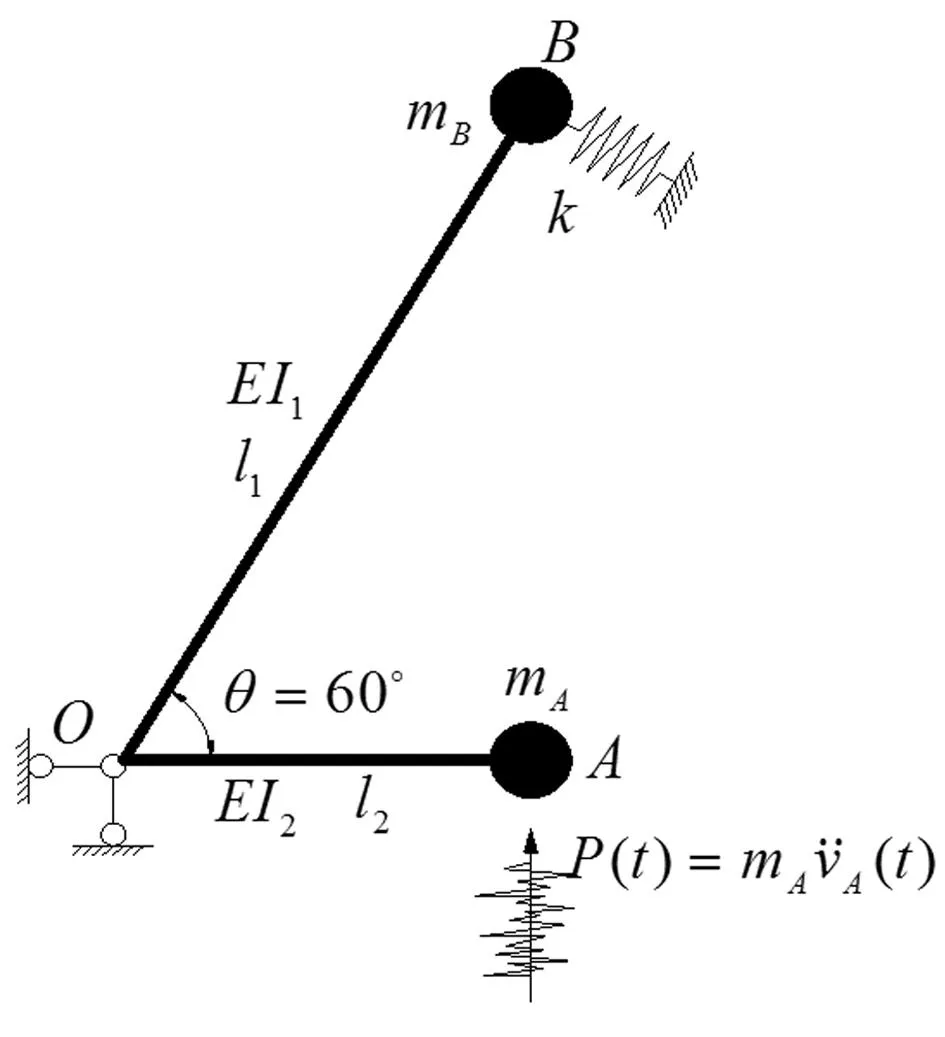
图4　改向扩展系统设计参数Fig.4 Expand system design parameters

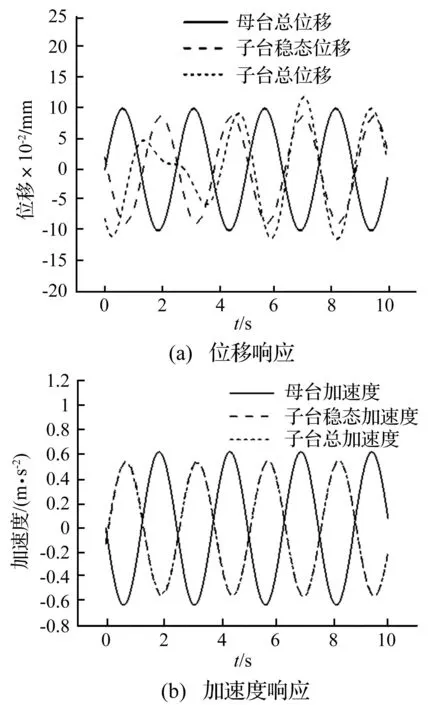
图5　子、母台位移及加速度对比Fig.5 Displacement and acceleration

图5(a)中子台总位移响应在振动若干周期之后与子台稳态位移响应趋于相等，这说明子台动力响应瞬态解衰减较快，系统反应可靠、稳定。图5(b)中子台的总加速度反应和稳态加速度反应相等(响应曲线重合)，系统加速度输出稳定。此外，通过对比图5中子台和母台的位移与加速度关系，发现子、母台动力行为存在振动相位滞后及动力响应幅值差异。

5结论

本文利用曲杆装置有改变方向的特性，根据达朗贝尔原理建立地震模拟振动台曲杆多向扩展系统模型，根据系统的动力分析与算例求解可得如下几点结论：

(1) 算例结果表明，母台的动力输入与子台动力输出有明显差异，在系统经过若干周期振动后，子台位移响应的瞬态解衰减消失，振动台扩展子台动力反应稳定。

(2) 扩展系统可以改变地震波的传递方向、相位和幅值。考虑曲杆刚度有限性，在改变方向过程中地震波的幅值和相位发生变化，该变化可通过改变曲杆杆件刚度、系统阻尼和质量分布来控制，并可在结构多点激励的研究中加以利用。

(3) 根据本文理论可对单向振动台进行设计改造，完成多向扩展，实现大跨结构的多点多向地震模拟振动台试验研究。

参 考 文 献

[ 1 ] 周颖,吕西林.建筑结构振动台模型试验方法与技术[M].北京:科学出版社,2012.

[ 2 ] Zerva A.Spatial variation of seismic ground motions: modeling and engineering applications [M].Florida: CRC Press Inc, 2009.

[ 3 ] 陈彦江,张德义,李晰.空间变化地震作用下钢管混凝土拱桥的抗震分析[J].工程力学,2013,30(12):99-106.

CHEN Yan-jiang, ZHANG De-yi, LI Xi.Stochastic seismic analysis of a CFST arch bridge under spatially varying ground motions [J].Engineering Mechanics, 2013, 30(12): 99-106.

[ 4 ] Konakli K, Der K A.Simulation of spatially varying ground motions including incoherence, wave-passage and differential site-response effects [J].Earthquake Engineering and Structural Dynamics, 2011, 41(3): 495-513.

[ 5 ] 赵建锋,杜修力,韩强,等.外源波动问题数值模拟的一种实现方式[J].工程力学,2007,24(4):52-58.

ZHAO Jian-feng, DU Xiu-li, HAN Qiang,et al.An approach to numerical simulation for external source wave motion [J].Engineering Mechanics, 2007, 24(4): 52-58.

[ 6 ] 杨昀,周列茅,周勇军.弯桥与高墩[M].北京:人民交通出版社,2011.

[ 7 ] 纪金豹,李晓亮,闫维明,等.九子台模拟地震振动台台阵系统及应[J].结构工程师,2011,27:31-36.

JI Jin-Bao, LI Xiao-liang, YAN Wei-ming, et al.Research on the shaking table array and dynamic model test [J].Structural Engineers, 2011, 27: 31-36.

[ 8 ] Clough R W, Penzien J.Dynamics of structures [M].New York: McGraw-Hill Inc, 1993.

[ 9 ] 亓兴军,李小军,申永刚.地震行波输入下大跨连续刚构桥梁半主动控制效应分析[J].振动与冲击,2007, 26(2):117-120.

QI Xing-jun, LI Xiao-jun, SHEN Yong-gang.Semi-activecontrol effect analysis for long-span continuous rigid-framed bridge under seismic travelling wave input [J].Journal of Vibration and Shock, 2007, 26(2): 117-120.

[10] 周国良,鲍叶欣,李小军,等.结构动力分析中多点激励问题的研究综述[J].世界地震工程,2009,25(4):25-32.

ZHOU Guo-liang, BAO Ye-xin, LI Xiao-jun, et al.Review on dynamic analyses of structures under multi-support excitation[J].World Earthquake Engineering,2009,25(4):25-32.

[11] 李忠献,史志利.行波激励下大跨度连续刚构桥的地震反应分析[J].地震工程与工程振动,2003,23(2): 68-76.

LI Zhong-xian, SHI Zhi-li.Seismic response analysis for long-span continuous rigid-framed bridges under excitation of traveling waves [J].Earthquake Engineering and Engineering Vibration, 2003, 23(2): 68-76.

[12] 屈铁军,王前信.多点输入地震反应分析研究的进展[J].世界地震工程,1993,1:30-38.

QU Tie-jun, WANG Qian-xin.Progress in the research on the seismic response analysis of multi-point input [J].World Earthquake Engineering, 1993, 1: 30-38.

Seismic simulation shaking table multidirectional expansion system

CHENGMai-li,LIQing-ning,WUDuo,BIYan-chao,MIAORu-song(School of Civil Engineering，Xi’an University of Architecture and Technology，Xi’an 710055, China)

Abstract:For the multidimensional, multipoint excitation vibration table test research of large-span space structures by using single vibration table, this paper put forth a seismic simulation shaking-table redirection extended system concept.Combined the characteristics of changed curved-bar mechanism on seismic wave propagation direction, the dynamics of the shaking table expand system was analyzed.Based on the multipoint excitation theory, considering the effect of superstructure inertia force to sub-units, the formula of the sub-units of equivalent mass was derived.Under the harmonic load, the multidirectional extended system dynamic response analytic expression was obtained.Studies show that multidirectional extended systems can effectively change the peak of seismic-wave acceleration, phase and the transfer direction; it is an effective method to achieve the large-span structure multipoint excitation test using a single shaking table.Examples show that the theory is correct; the method is reliable.

Key words:shaking table; extended system; multidimensional multipoint; curved-bar mechanism

中图分类号:TU311.3;TU317+.1

文献标志码：A

DOI:10.13465/j.cnki.jvs.2016.08.012

通信作者李青宁 男，教授，博士生导师，1952年4月生

收稿日期：2014-11-11修改稿收到日期：2015-03-25

基金项目：国家自然科学基金(51078306)；国家青年基金项目(51408453)；高等学校博士学科点专项科研基金(20106120110004)；陕西省自然科学基础研究计划资助项目(2013JQ7007)

第一作者 程麦理 男，博士生，1987年6月生

E-mail：liqndq@xauat.edu.cn