具时滞阶段结构和非线性发生率的SIS模型*

童姗姗， 仝云旭

(南阳理工学院 数理学院，河南 南阳 473000)



具时滞阶段结构和非线性发生率的SIS模型*

童姗姗， 仝云旭

(南阳理工学院 数理学院，河南 南阳 473000)

摘要：研究了一类具有时滞、阶段结构和非线性发生率的SIS传染病模型；讨论了平衡点的存在性，并利用Routh-Hurwits判据和超越函数零点判别法探究了平衡点的局部渐近稳定性,给出了此类传染病平衡点的局部渐近稳定性的判定定理，结论为卫生部门的疾病防控工作提供了一定的理论支持.

关键词：时滞；阶段结构；非线性发生率；局部渐近稳定性

种群的增长都有成长发育的过程，不同年龄阶段的种群表现不同的特征，因此考虑具有年龄阶段的传染病模型更具有实际意义[1].近些年来，已有许多学者研究了具有年龄阶段的传染病模型，文献[2-4]讨论了具有阶段结构和分布时滞的传染病模型,文献[5-7]研究了具有阶段结构和非线性发生率的传染病模型.

研究一类种群具有恢复期时滞、两个阶段结构和非线性发生率的SIS传染病模型.

假设传染病仅在成年阶段传播，幼年阶段不会感染此类传染病，把成年阶段分为易感染者和染病者两类，考虑非线性传染率，建立如下SIS传染病数学模型：

(1)

其中X(t),S(t),I(t)分别表示t时刻幼年个体的数目、成年易感者的数目、成年感染者的数目，a表示种群的出生率，r表示种群幼年个体的自然死亡率，b表示幼年个体的成熟率，δ表示成年个体的自然死亡率，βI(t)S2(t)表示疾病的发生率，d表示感染者的死亡率，d=δ+ε，ε表示感染者的因病死亡率，α表示感染者的恢复率，τ≥0为恢复期时滞，根据生态学意义，a、r、b、δ、A、β、d、ε、α都为正常数.

1平衡点的存在性

令方程组右端为零，可得

解得系统(1)在G内有平凡平衡点E0(0,0,0).当ab-δ(b+r)>0时式(1)在G内有唯一疾病平衡点E*(X*,S*,I*).

其中

为讨论方便记

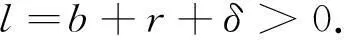
2平衡点的稳定性[8-9]

定理1当m>0时，平衡点E0(0,0,0)不稳定;当m<0时，E0(0,0,0)是局部渐近稳定的.

证：系统在E0(0,0,0)处的雅可比行列式为

特征方程为

(2)

对于超越方程

假设其至少有一个非负实部的根u+iv(u>0)，代入得

分离实部虚部得

这与假设矛盾.故超越方程的根都具有负实部.

对于方程

(3)

令

则有

当m>0时p>0,q<0,Δ>0，方程(3)有一负实部特征根和一正实部特征根，即特征方程(2)有一正实部特征根，E0(0,0,0)不稳定;

当m<0时p>0,q>0,Δ>0，方程(3)有两负实部特征根，此时特征方程(2)的特征根均具有负实部，E0(0,0,0)是局部渐近稳定的.证毕.

定理2当m>0时，即E*(X*,S*,I*)存在时，若满足

则对任意的滞后时间λ≥0，系统(1)的疾病平衡点是局部渐近稳定的.

证：为求E*(X*,S*,I*)的近似线性，作x=X-X*,s=S-S*,i=I-I*,为叙述方便，仍用X,S,I记x,s,i，得系统(1)在E*(X*,S*,I*)处的近似线性系统为

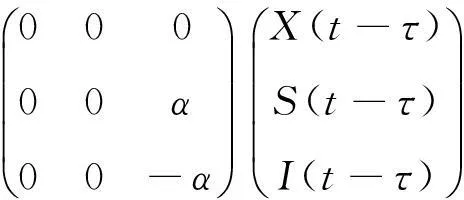
特征矩阵为

特征方程为

(4)

其中：

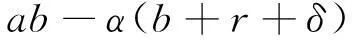
当τ=0时，特征方程式(4)变为

(5)

由于

由Routh-Hurwits判据知方程(5)的根均具有负实部，即当τ=0时，疾病平衡点E*(X*,S*,I*)局部渐近稳定.

假设存在τ>0使特征方程(4)有纯虚根λ=±iω(ω>0),代入特征方程(4)中可以得到

分离实部和虚部得到

(6)

(7)

式(6)和式(7)两边同时平方得到

令ω2=μ，则得到

令

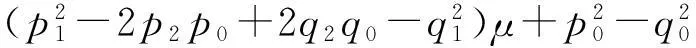
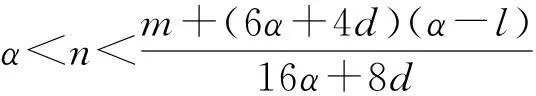
(2βS*I*+b+r+δ-α)2-2[2βS*I*(b+d+r)+δ(b+r)-ab-α(b+r+δ)]-α2=

(2βS*I*+b+r+δ)2-2α(2βS*I*+b+r+δ)+α2-4βS*I*(b+r+d)+2[ab-δ(b+r)]+2α(b+r+δ)-α2=

2[ab-δ(b+r)]+(b+r+δ)2+4β2S*2I*2+4βS*I*(δ-α-d)=

2[ab-δ(b+r)]+(2βS*I*+δ-α-d)2+(b+r+d+α)(b+r+2δ-α-d)=

2[ab-δ(b+r)]+(2βS*I*+δ-α-d)2+(b+r+d+α)(l-ε-α) > 0

[2βS*I*(b+d+r)+δ(b+r)-ab-α(b+r+δ)]2+2α[αδ(b+r)-αab]+2(2βS*I*+b+r+δ-α)

[(b+r)(2dβS*I*-αδ)+αab]-[α(b+r+δ)]2=

4β2S*2I*2(b+r+d)2+[ab-δ(b+r)]2-4βS*I*α(b+r+d)(b+r+δ)+2α[ab-δ(b+r)](b+r+δ-α)-4βS*I*α[ab-δ(b+r)]+2[ab-δ(b+r)](2d+3α)(2βS*I*+b+r+δ-α) > 4βS*I*(b+r+d)2(βS*I*-α)+[ab-δ(b+r)][ab-δ(b+r)-4βS*I*α-2(2d+3α)(2βS*I*+b+r+δ-α)]=

4βS*I*(b+r+d)2(n-α)+m[m-4nα-2(2d+3α)(2n+l-α)] > 0

(p0+q0)[(b+r)(2βS*I*d-αδ)+αab-αδ(b+r)+αab]=

2(p0+q0)[αab+(b+r)(βS*I*d-αδ)]=

2(p0+q0){αab-αδ(b+r)+(d+α)[ab-αδ(b+r)]}=

2(p0+q0)(d+2α)[ab-δ(b+r)]=2m(p0+q0)(d+2α)>0

综上有g(μ)>0,与g(μ)=0矛盾.故此时，特征方程(4)没有纯虚根，方程(4)的根皆具有负实部.故当满足条件H1,H2时,对任意的滞后时间τ>0系统的疾病平衡点是局部渐近稳定的.证毕.

3结论

利用Routh-Hurwits判据和超越函数零点判别法分别讨论了平凡平衡点与疾病平衡点的局部渐近稳定性的充分条件,从而给出了此类传染病平衡点的局部渐近稳定性的判定定理，为人类研究疾病的传播提供了一定的理论依据.

参考文献(References)：

[1]马知恩,周义仓,王稳地,等.传染病动力学的数学建模与研究[M].北京：科学出版社,2007

MA Z E,ZHOU Y C,WANG W,et al.Mathematical Modeling and Research on Dynamics of Infectious Diseases[M].Beijing:Science Press，2007

[2] XIAO Y N,CHEN L S.Analysis of a SIS Epidemic Model with Stage Structured and a Delay[J].Communications in Nonlinear Science & Numerical Simulation,2000,6(1):35-39

[3] WU C F,WENG P X.Stability Analysis of a SIS Model with Stage Structured and Distributed Maturation Delay[J].Nonlinear Analysis,2009,71(5):892-901

[4] 王文娟,辛京奇.一类具有阶段结构和分布时滞的种群-传染病模型[J].数学的实践与认识,2010,40(14)：114-120

WANG W J,XIN J Q.An Populaition-Epidemic Model with Distribution Delay and Stage Structure[J].Mathematics in Practice and Theory,2010,40(14):114-120

[5] 徐文雄,张仲华.年龄结构SIR流行病传播数学模型渐近分析[J].西安交通大学学报,2003,37(10):1086-1089

XU W X,ZHANG Z H.Asymptotic Analysis of an Age-Dependent SIR Epidemic Model[J].Journal of Xi'an Jiao Tong University,2003,37(10):1086-1089

[6] 张素霞,谢妮,胡钢,等.一类具有染病年龄结构流行病模型渐近分析[J].西安理工大学学报,2008,24(4):495-498

ZHANG S X,XIE N,HU G,et al.Asymptotic Behavior of an Epidemic Model with Infection-Age-Dependence[J].Journal of Xi’an University of technology,2008,24(4):495-498

[7] 曹瑾,唐蕾,武佳,等.具饱和传染率和时滞两阶段结构的传染病模型[J].数理医药学杂志,2013,(3):260-263

CAO J,TANG L,WU K,et al.Analysis of a Delayed Epidemic Model with Two Stage-Structure and Saturation Incidence[J].Journal of Mathematical Medicine,2013,(3):260-26

[8] 陈爱珍,周宗福.一类非线性退化时滞微分系统的一致稳定性[J].重庆工商大学学报(自然科学版),2014,31(11):4-9

CHEN A Z,ZHOU Z F.Uniform of a Class of Nonlinear Degenerate Differential System with Delay[J].Journal of Chongqing Technology and Business:Natural Sciences Edition,2014,31(11):4-9

[9] 吴禧,周宗福.脉冲时滞微分方程的渐近稳定性分析[J].重庆工商大学学报(自然科学版),2014,31(7):1-3

WU X,ZHOU Z F.Analysis of Asymptotic Stability of Impulsive Differential Equation with Delay[J].Journal o f Chongqing Technology and Business:Natural Sciences Edition,2014,31(7):1-3

责任编辑：田静

SIS Epidemic Model with Time Delay，Stage-structrue and Nonlinear Incidence

TONG Shan-shan, TONG Yun-xu

(College of Mathematics and Physics,Nanyang Institute of Technology,Henan Nanyang 473004,China)

Abstract：A class of an SIS epidemic model with delay，stage-structure and nonlinear incidence is established and analyzed. The existence of equilibrium points is discussed and its local asymptotic stability of equilibrium is discussed by the Routh-Hurwits and transcendental function zero distinction. Furthermore,the determinating theorem for the local asymptotic stability of this class of the epidemic is given, the conclusion provides some theoretical support for the disease control and prevention in the health sector.

Key words：delay; stage-structure; nonlinear incidence; local asymptotic stability

中图分类号：O175.1

文献标志码：A

文章编号：1672-058X(2016)02-0001-04

作者简介：童姗姗(1986-)，女，河南南阳人，助教，硕士，从事应用数学模型与微分方程研究.

*基金项目：陕西省自然科学基金项目(2014JM1019)；陕西省教育厅科研基金项目(14JK1225).

收稿日期：2015-09-26；修回日期：2015-11-28.

doi:10.16055/j.issn.1672-058X.2016.0002.001