基于EEMD和小波神经网络的短期电价组合预测*

郭 欣 欣

(安徽工程大学 电气工程学院,安徽 芜湖 241000)



基于EEMD和小波神经网络的短期电价组合预测*

郭 欣 欣

(安徽工程大学 电气工程学院,安徽 芜湖 241000)

摘要：从降低电价序列非平稳性出发，提出一种基于聚类经验模态分解(EEMD)和小波神经网络(WNN)的新型组合预测模型来预测短期电价；采用Matlab/Simulink仿真平台进行建模仿真；仿真结果表明：新算法预测精度高，预测方法可行。

关键词：电价；预测；聚类经验模态分解；小波神经网络；混合模型

电价预测在电力市场运行过程中对风险管理、决策投资以及监督管理具有不可或缺的意义。目前的预测方法都对电价的预测做出了卓越贡献[1-7]。从目前检索到的有关电价的文献资料来看，电价时间序列具有非正态性[8-9]，比如“尖峰、有偏”，这跟电价受多种复杂信息影响有关。纵观所有电价预测方法，其实质是直接拟合电价与其影响因素之间的“黑箱”模型，减少中间环节的不良影响，虽然取得了一定效果，但是由于电价本身的特性没有得到深度挖掘，预测效果过度依赖于“黑箱”模型的性能。因此短期电价预测应从深度挖掘电价特性出发，基于电价特点，针对性地选择多种算法，通过算法本身优势互补来建立组合预测模型。

电价预测的核心问题是预测的技术问题，或者说是预测的数学模型。从文献[8-9]对电力市场分布特性的研究来看，电价本身的运动规律是非线性的，也可能是非正态的，很难用清晰的数学表达式来表达电价及其影响变量间的关系。而小波神经网络预测模型恰好是一种非线性、自适应信息处理系统，是一种非精确数学模型方法。电价的非线性和非平稳性是影响预测效果的主要原因，因此对电价信号进行一定尺度或波动趋势的有效分解可减低电价信号的非平稳性。此处从研究降低电价序列非平稳性出发，提出一种基于聚类经验模态分解和小波神经网络(EEMD-WNN)的组合短期电价预测模型，预测精度高，具有一定参考价值。

1聚类经验模态分解(EEMD)

文献[10]对经验模态分解(EMD)进行了详细的介绍，经验模态分解相对于传统的小波分解算法减少了人为因素对分解结果造成的影响，具有一定的先进性，但上述算法在一些情况下会出现模态混叠现象。针对EMD的模态混叠问题，此处采用一种利用高斯白噪声辅助分析的新方法，即聚类经验模态分解(EEMD)[11-12]。聚类经验模态分解步骤如下：

1) 将高斯白噪声序列{nm(t)}加入到电价序列{x(t)}中，得到加噪的待处理信号{xm(t)}：xm(t)=x(t)+knm(t)，并用EMD分解xm(t)为若干IMF；

2) 平均化IMF整体值，将其作为{x(t)}的最终分解结果。

聚类经验模态分解有效地解决了信号模态混叠的问题并最大程度地保留了原序列的真实性，根据参考文献[10]，加入的白噪声序列服从(0，(αε)2)的正态分布，为了取得比较好的分解结果，r取100，α取0.1。

2小波神经网络结构

多个参考文献对WNN拓扑结构均有论述，此处主要参考文献[13]，选取Morlet母小波基函数作为小波基函数，数学表达式如下：

(1)

小波神经网络采用如下方式进行修正以逼近期望结果：

1) 计算网络预测误差：

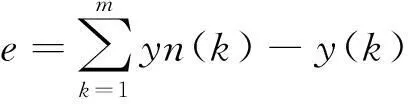
(2)

yn(k)为期望输出，y(k)为小波神经网络预测输出。

2) 根据e值修正WNN权值和基函数系数：

(3)

(4)

式(4)中，η为学习速率。

3实例仿真

3.1模型建立

根据前面的论述，建立基于EEMD-WNN的组合短期电价预测模型结构流程如图1所示：

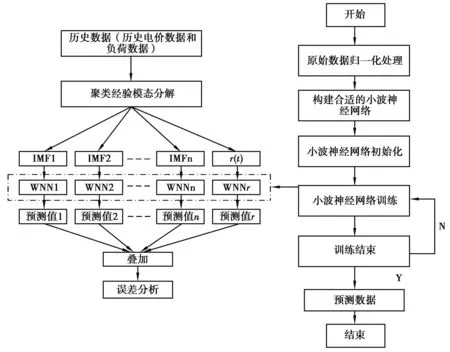
图1　基于EEMD及小波神经网络预测模型结构图Fig.1　Model structure of electricity price forecasting based on EEMD-WNN

3.2样本选择与处理

为验证所提方法的可行性，选取电价规律性较好的美国加州电力市场的历史运行数据作为样本进行模拟和预测。

图2是2010年8月1日到2010年9月13日原始电价序列。为检验预测效果，将其与其他3种模型进行比较。第1种模型不考虑负荷因素，电价未作分解，直接使用传统神经网络进行预测，简称模型1；第2种，电价序列进行分解，负荷序列不分解，对电价进行预测(简称模型2)；第3种模型分解后，采用径向基神经网络预测(简称模型3)；此处方法简称模型4。误差指标MAPE作为评价模型性能的指标，MAPE定义如下[14]：

(6)

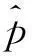
用2010年8月1号到2010年9月12号的历史电价及其对应的历史负荷数据为样本数据进行小波神经网络的训练，图2为电价序列图。训练后利用2010年9月13号的负荷数据对2010年9月13号的电价进行预测，图3为EEMD分解原始电价序列结果图，从图3可以看出EEMD分解得到的信号比较平稳，为准确预测打下基础。表1为部分时段电价原始值与预测值，表2为各方法日平均绝对百分比误差。

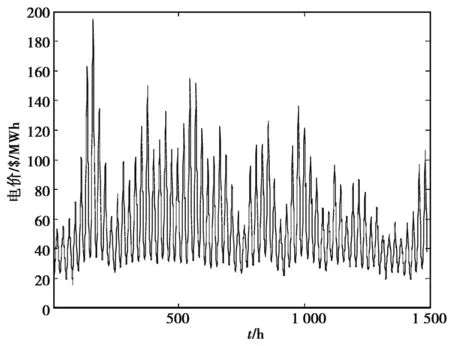
图2　原始电价序列图Fig.2　Time series of electricity price signal

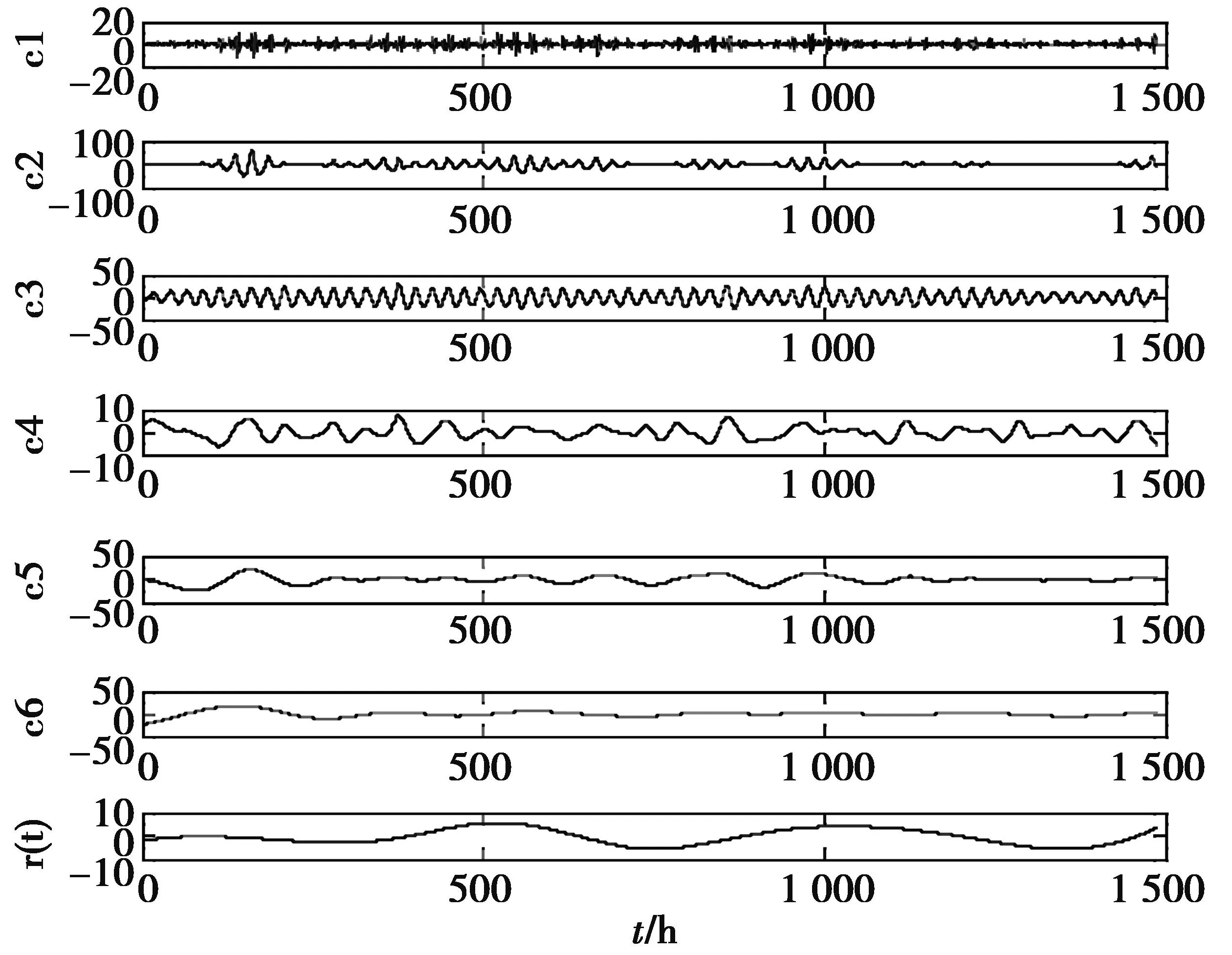
图3　EEMD分解电价序列结果Fig.3　EEMD results of electricity price signal

时 段012345678原值($/MWh)预测($/MWh)30.6730.7425.6725.0524.3125.0522.1922.7721.6321.9522.4622.9625.3825.7333.633.9433.5233.54

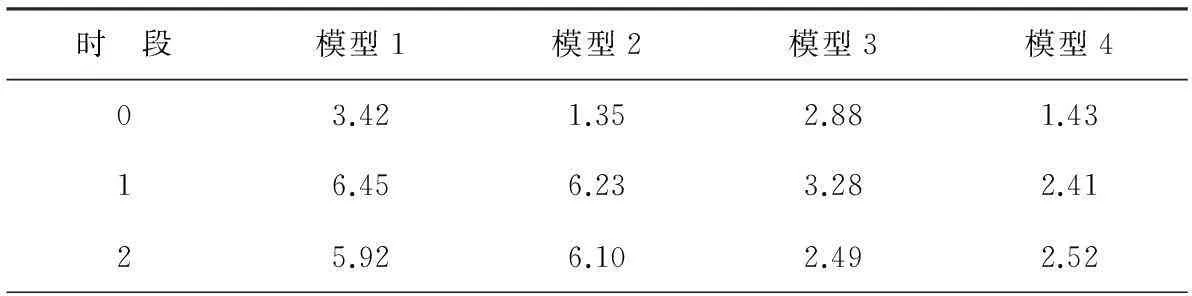
表2　4种模型的MAPE误差比较

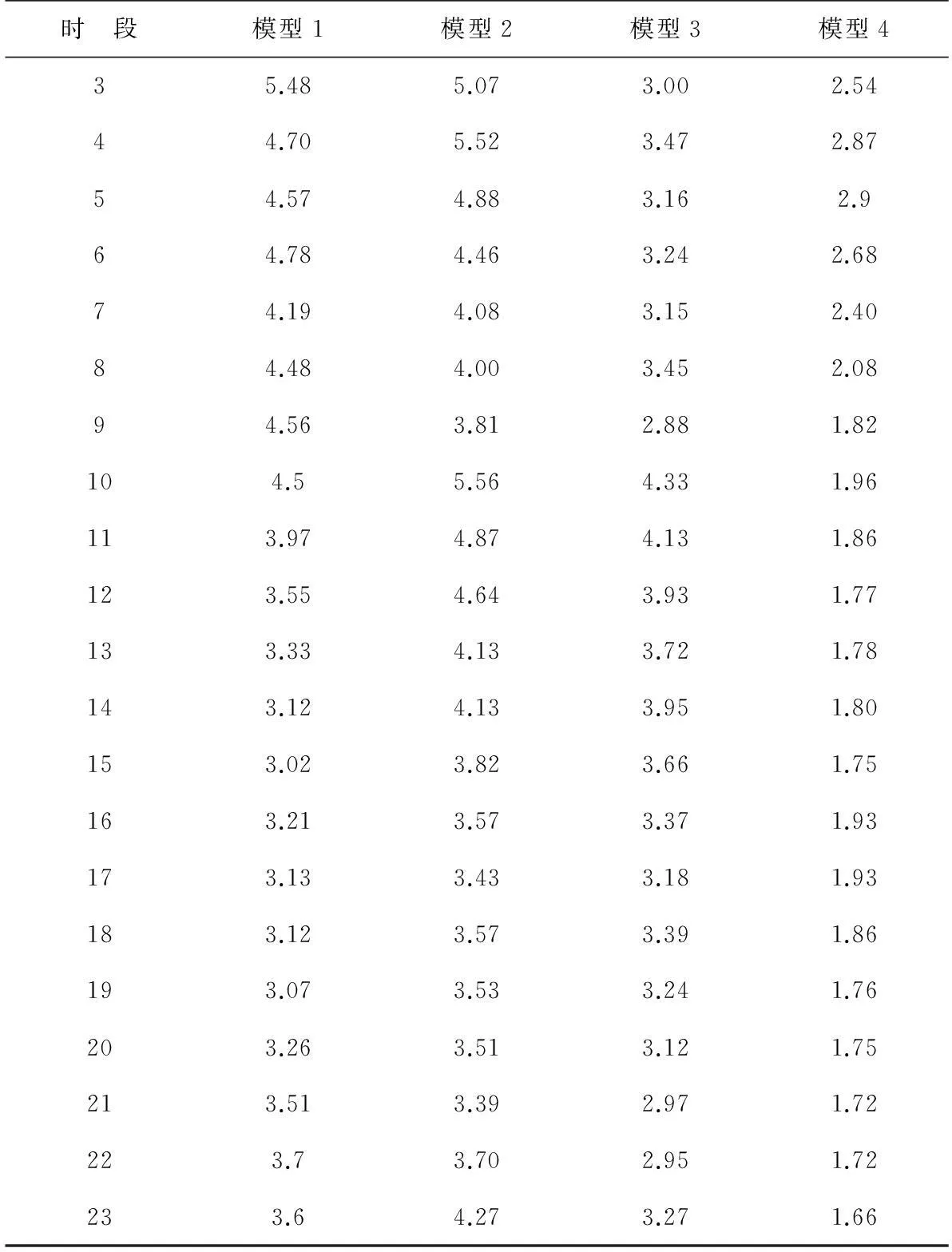
续表2　%

从表2可以看出，尽管负荷跟电价密切相关，但直接引入负荷因素，对电价的预测效果并不理想，此处组合预测模型从降低电价序列的非平稳性出发，引入关联性较大的负荷因素，并对其进行分解，以更好反应电价变化的特征，使得预测精度有了很大提高。

4结论

采用EEMD及小波神经网络相结合的方法对美国加州电力市场电价进行预测与分析，预测流程简单，可操作性强，预测结果准确度高，工程应用价值大。同时也可看出，像电价这种受多种不确定因素影响的时间序列，组合预测模型比之单一模型更能提高预测精度。

参考文献(References)：

[1]胡朝阳,孙维真,汪震,等.考虑市场力的短、中、长期电价预测[J].电力系统自动化，2003，27(22)：16-22

HU ZH Y，SUN W ZH，WANG ZH，et al.Short-term，Medium-term and Long-term Forecasting of Electricity Price with Consideration to Market Power[J].Automation of Electric Power Systems，2003，27(22)：16-22

[2] HU Z，YU Y，WANG Z，et al.Price Forecasting：Using an Integrated Approach[C]∥IEEE International Conference on Electric Utility Deregulation，Restructuring and Power Technologies.HongKong，China，2004

[3] HONG Y，HSIAO C.Location Marginal Price Forecasting in Deregulated Electric Markets Using a Recurrent Neural Network[C]∥IEEE PES Winter Meeting Columbus OH USA,2001

[4] GUO J J，LUH P B.Selecting Input Factors for Clusters of Gaussian Radial Basis Function Networks to Improve Market Clearing Price Prediction[J].IEEE Transactions on Power Systems，2003,18(2)：665-672

[5] YAMIN H Y，SHAH I S，LI Z.Adaptive Short-term Electricity Price Forecasting Using Artificial Neural Networks in the Restructured Power Markets[J].Electrical Power and Energy Systems，2004，26(8)：571-581

[6] 杨洪明，段献忠.电价的混沌特性分析及其预测模型研究[J].电网技术,2004,28(3)：60-64

YANG H M,DUAN X ZH.Research on Chaotic Characteristics of Electricity Price and Its Forecasting Model[J].Power System Technology，2004，28(3)：60-64

[7] 田丽.基于SVM和神经网络组合预测模型物流需求预测[J].重庆工商大学学报(自然科学版)，2012,29(9)：61-64

TIAN L.Research on Logistic Demand Forecast Based on Support Vector Machines and Neural Network[J].Journal of Chongqing Technology and Business University(Natural Science Edition),2012,29(9)：61-64

[8] 刘西陲.系统边际电价概率分布检验及模型研究[J].中国电机工程学报,2009,29(2):72-78

LIU X CH.Study on Probability Distribution and Model of System Marginal Price[J].Proceeding of the CSEE,2009,29(2):72-78

[9] 郑华.系统边际价格概率分布的实证分析[J].中国电机工程学报,2006,26(3)：43-48

ZHANG H.Positivism Analysis on the Probability Distribution of System Marginal Price[J].Proceeding of the CSEE,2006,26(3)：43-48

[10]HUANG N E,SHEN Z,LONG S R.The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-stationary Time Series Analysis[J].Proceedings of the Royal Society Scotland,1998,454(1971): 903-995

[11] WU Z,HUANG N E.Ensemble Empirical Mode Decomposition:A Noise-assisted Data Analysis Method[J].Advances in Adaptive Data Analysis,2009(1): 1-41

[12] 王贺.基于经验模态分解分解和小波神经网络的短期风功率组合预测[J].电工技术学,2013,28(9):137-145

WANG H.A Hybrid Model for Wind Power Forecasting Based on Ensemble Empirical Mode Decomposition and Wavelet Neural Networks[J].Transactions of China Electrotechnical Society,2013,28(9):137-145

[13] 王小川.Matlab神经网络43个案例分析[M].北京：北京航空航天大学出版社，2013

WANG X CH.43 Case Analysis of Neural Network by Matlab[M].Beijing：Beijing University of Aeronautics and Astronautics Press,2013

[14] 张金良.短期电价预测的组合混沌方法[J].中国管理科学，2011,19(2)：133-140

ZHANG J L.Short Term Electricity Price Forecasting of Combined Chaotic Method[J].Chinese Journal of Management Science，2011,19(2)：133-140

责任编辑：李翠薇

Combined Forecast for Short-term Electricity Price Basedon EEMD and Wavelet Neural Network

GUO Xin-xin

(School of Electrical Engineering, Anhui Polytechnic University, Anhui Wuhu 241000, China)

Abstract：Based on the non-stationary of electricity price sequence, this paper proposes a new combined forecast model to forecast short-term electricity price based on ensemble empirical mode decomposition (EEMD) and wavelet neural network (WNN), and uses Matlab/Simulink simulation platform to model. The simulation results show that the new algorithm has high forecasting accuracy and the forecasting method is feasible.

Key words：electricity price; forecast; ensemble empirical mode decomposition (EEMD); wavelet neural network (WNN); hybrid model

中图分类号：TM715

文献标志码：A

文章编号：1672-058X(2016)02-0021-05

作者简介：郭欣欣(1980-)，女，河南永城人，讲师，从事电力系统自动化及微电网研究.

*基金项目：安徽工程大学青年科研基金资助项目(KZ00313033).

收稿日期：2015-10-01；修回日期：2015-11-24.

doi:10.16055/j.issn.1672-058X.2016.0002.005