基于PSO的一类线性系统参数辨识方法研究*

李　珍， 魏利胜**， 程运昌

(1.安徽工程大学 电气工程学院,安徽 芜湖 241000；2.国网霍邱县供电有限责任公司,安徽 六安 237400)



基于PSO的一类线性系统参数辨识方法研究*

李珍1， 魏利胜1**， 程运昌2

(1.安徽工程大学 电气工程学院,安徽 芜湖 241000；2.国网霍邱县供电有限责任公司,安徽 六安 237400)

摘要：研究了一种线性系统的参数精确辨识方法；首先采用PSO(Particle Swarm Optimization，粒子群优化)方法对模型进行优化迭代，并选择合适误差准则作为粒子群优化算法的适应度函数，以迭代每个粒子所对应的参数速度和大小；在此基础上，寻找最小适应度值的粒子，推导出最优的适应度函数值，实现系统参数的实时、精确估计；最后通过实验验证了基于粒子群优化算法的参数辨识法的准确性和有效性。

关键词：参数辨识；PSO方法；准则函数

系统辨识是一种数学表达式，主要用于建立其状态参数之间及其与外作用的相互作用、相互制约的关系[1-2]。建立一个合适的数学模型，将为后续的系统控制提供较大的帮助，可以帮助人们对系统本质特征有一个更加充分的认识。而系统辨识就是一种利用系统运行或试验的输入输出数据建立系统的数学模型的理论和方法，被广泛地应用于工业控制、医学辅助等众多领域。由于实际研究对象通常都非常复杂，且内部激励不完全清楚，导致其数学模型很难直接获取。因此，许多科研工作者根据系统辨识方法对对象模型进行参数估计。

朱呈祥等[3]向人们提出了又一种辨识的方法，针对线性系统引入一种PIλDμ控制器来实现辨识，用被滤波的差值传递方程刻画出一个动态的过程，控制系统是以差值为状态变量，同时通过解决使用状态反馈方法使得误差系统状态渐进稳定的问题，达到辨识误差的校正与限制。俞林宏等[4]提出了利用递推空间的辨识方法，依据传播函数把对应的能观矩阵进行分解，能观矩阵的更新是依据递推的最小二乘法准则、线性算子以及递推的估计传播函数。程轶平等[5]研究了关于形态空间的辨识方法，在求出系统中预估器的马儿可夫参数、状态序列、预估器的可观性矩阵之间的成积矩阵之后，再次依据多元的线性回归求出它的各个矩阵来实现参数的辨识。徐晓龙等[6]运用了粒子群的优化方法，将最大的似然标准看作适应度的函数，通过粒子群算法将参数估计问题转变为目标优化问题。文献[7]中，应用了离线的ARX(Auto-Regression with eXog-enous variables，有源自回归)法和在线遗忘因子的RARX法(Recursive ARX，递推式有源自回归)，根据地震响应的记录数据来对建筑物在地震损伤中时变与时不变的参数进行估计。这些方法都有一定的局限性，有的需要矩阵必须是可观测的，实际中ARX模型可能会出现丢失和虚假模态的情况，并且在大型或复杂系统中，RARX法的适用性还有待检验。

通过对现有的辨识方法的比较和分析，并考虑到PSO优化方法具有速度非常快、调整参数少，且不要求矩阵的可观测性与结构是否复杂等特点[8]，拟将PSO方法引入到系统参数的实时估计中。在利用PSO方法的参数具体估计过程中，将误差准则函数作为该算法的适应度函数，粒子参数的速度与大小更新根据该算法的公式来完成。对于速度与大小的更新，是同时根据历史数据和本次数据来计算得到下次的速度与大小，数据可靠性将更高。对于线性系统的参数估计，分别采用该算法与最小二乘遗传递推算法，分析其收敛性与准确性，为以后更多不同系统中的参数估计提供辨识的基础。

1粒子群优化算法基本原理

自1995年PSO方法首次被提出以来，得到了研究者的青睐。PSO方法属于进化计算方法中的一种新方法[9-10]，具有系统一开始就要给予每一个粒子一个随机的速度，同时保证每个粒子可以在整个问题空间流动；每一个粒子都是记忆粒子；粒子的进化是经过粒子之间的淘汰与协作来实现的等特点；同时，PSO具有手动调整参数较少，相关编程简单等诸多优点，致其发展速度非常迅速[1]。

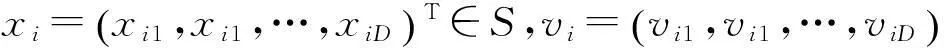
步骤1：在给定的搜索区域当中，随机产生粒子的位置大小与速度来初始化粒子群。

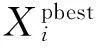
步骤3：对i=1,2,…,N，求出整个粒子群中的gbest和pg，即全部粒子中所搜索到的最优的适应度与全部粒子中所搜索到的最优位置。

步骤4：对i=1,2,…,N，表示出粒子i在当前位置xi处的适应度值fitnessi。

步骤5：粒子的位置大小与速度按照下面的式子来变换：

(1)

(2)

(3)

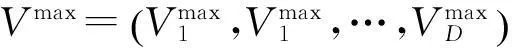
(4)

式(4)中，wmax、wmin分别是w的最大与最小值；t、Tmax分别是当前进化次数与最大进化次数。

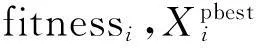
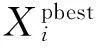
步骤8：当算法中的适应度值gbest小于了事先设定好的阈值ε时或则到达了最大的循环次数Tmax，就终止计算，不然就转接到步骤4。

2基于粒子群优化算法的系统参数辨识

在系统辨识中，主要考虑一类单输入单输出动态系统[12]，其参数辨识结构图如图2所示。

图1中，系统的输入u(k)与输出z(k)是都是可以观测的；系统的模子由G(z-1)来表示，其形容了系统的输入与输出的特征，系统的实际输出则取y(k)来表达。而N(z-1)则是噪声的模型，设定不相关的随机噪声v(k)的均值为零。通常情况下：

其中A(k)、B(k)、C(k)和D(k)分别为

当系统选取滑动模型时，则

(5)

若假定模型阶次na，nb和nd已经确定，并令

将式(5)化为最小二乘格式，可得：

(6)

基于PSO系统辨识的实质问题也就是将辨识问题作为优化问题来考虑。对于SISO动态系统的模型：

(7)

式(7)中：z(k)表示系统的输出；u(k)表示系统的输入信号；零均值且方差为σ2的高斯白噪声由v(k)来表示，v(k)与u(k)相互之间是独立的。

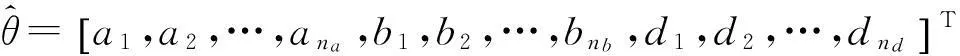
(8)

从进化计算的角度讲，将J(θ)作为粒子群优化算法中的适应度函数，基于PSO参数辨识的目的是使J(θ)最小，则其对应的位置即为被辨识的参数。由于极小化式(8)是属于在线优化问题，可以采用PSO算法求式(8)的极小值及其对应的模型参数。

3仿真实验

依据被辨识系统的真实的输入-输出数据，从已知的一组类似模型中来选择出一个与待辨识系统等价的系统模型。然后再利用MATLAB软件进行编程。利用粒子群优化算法和最小二乘遗传递推算法来实现系统辨识的仿真，给出系统辨识的仿真全过程，可以将其作为实际的工程中的一个简单的基础知识[12]。

对于系统的两种辨识方法即粒子群优化算法和最小二乘遗传递推算法的仿真结果为

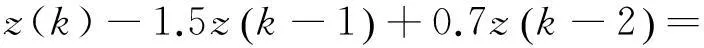
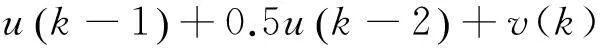
(9)

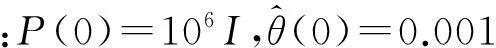
模型产生的随机输入信号和随机噪声信号如图3所示，图中噪声信号的不同颜色代表了不同的维数，噪声信号是一个L×L维的信号。

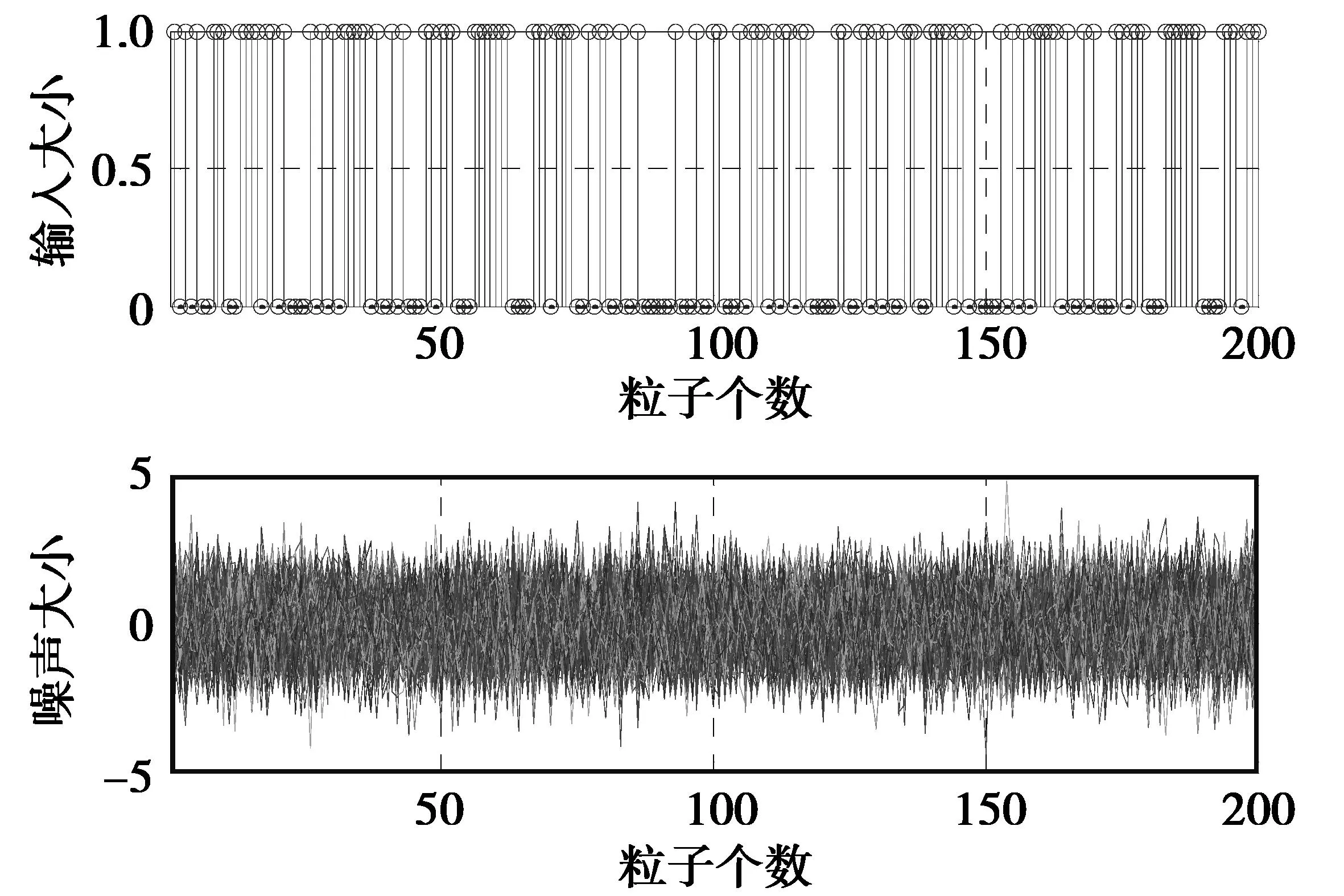
图3　模型的输入信号图和噪声信号图Fig.3　Input signal and noise signal of the model

对于待辨识参数而言，比较两种辨识算法的仿真图。图4是采用粒子群优化方法来进行系统的参数估计，应用式(8)作为适应度函数的参数仿真图，图5是采用最小二乘遗传递推方法来进行系统的参数估计。两图比较可见，在图4中辨识的参数最早的只需要5次左右的循环就趋于收敛了，最晚也只需要35次左右的循环就趋于收敛了，且每个参数的波动性都比较平缓。而在图5中辨识的参数最早的需要10次左右的循环才趋于收敛，最晚的需要120次左右的循环才趋于收敛，且相比而言每个参数的波动性要大。由图4可以看得出，参数a1在循环次数达到20次就开始趋于收敛，循环次数达到40次的时候，参数的估计值就不再抖动，保持在-1.5不变了；由图5可以看得出，参数a1在循环次数达到40次才开始趋于收敛，循环次数达到170次的时候，参数的估计值就几乎不再抖动，保持在-1.325 7了。同理其他参数的比较也可以看出。由此可知，粒子群的优化算法相比较最小二乘遗传递推算法可以更准确和快速的估计出参数。

从图4、图5中可得出两种辨识方法估计出来的参数大小见表1。

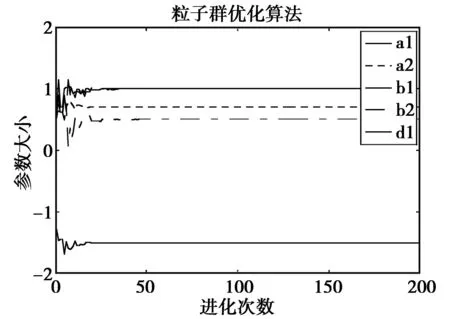
图4　基于粒子群优化算法的辨识参数Fig.4　Recognition paramther based on PSO

图5　最小二乘遗传递推算法的辨识参数[10]Fig.5　Recognition parameter of deduction algorithm of least square

参数a1a2b1b2d1实际值-1.50.710.51文献[10]方法-1.32570.62241.04410.53590.0291方法-1.50.710.51

从表1中可知，PSO方法可以确切的估计出参数的大小，a1=-1.5、a2=0.7、b1=1、b2=0.5、d1=1。与最小二乘遗传递推算法相比较而言，粒子群优化算法具有辨识精确的特点。

图6是采用粒子群的优化方法来进行的参数估计，图7是采用最小二乘遗传递推方法来进行的参数估计。两图比较可见，在图6中有噪声的系统输出与模型辨识输出的图形几乎是90%多的吻合，误差范围在-0.5～1.5。在图8中有噪声的系统实际输出与模型辨识输出的图形有60%左右的吻合度，它们的误差变化范围在-10～5之间。相比较而言图6误差图形比图7误差图形的波动要平缓得多。由此可见，运用粒子群的优化算法相比较最小二乘遗传递推算法可以使辨识输出值与系统的实际输出值之间的误差更小，体现了方法的准确性更高。

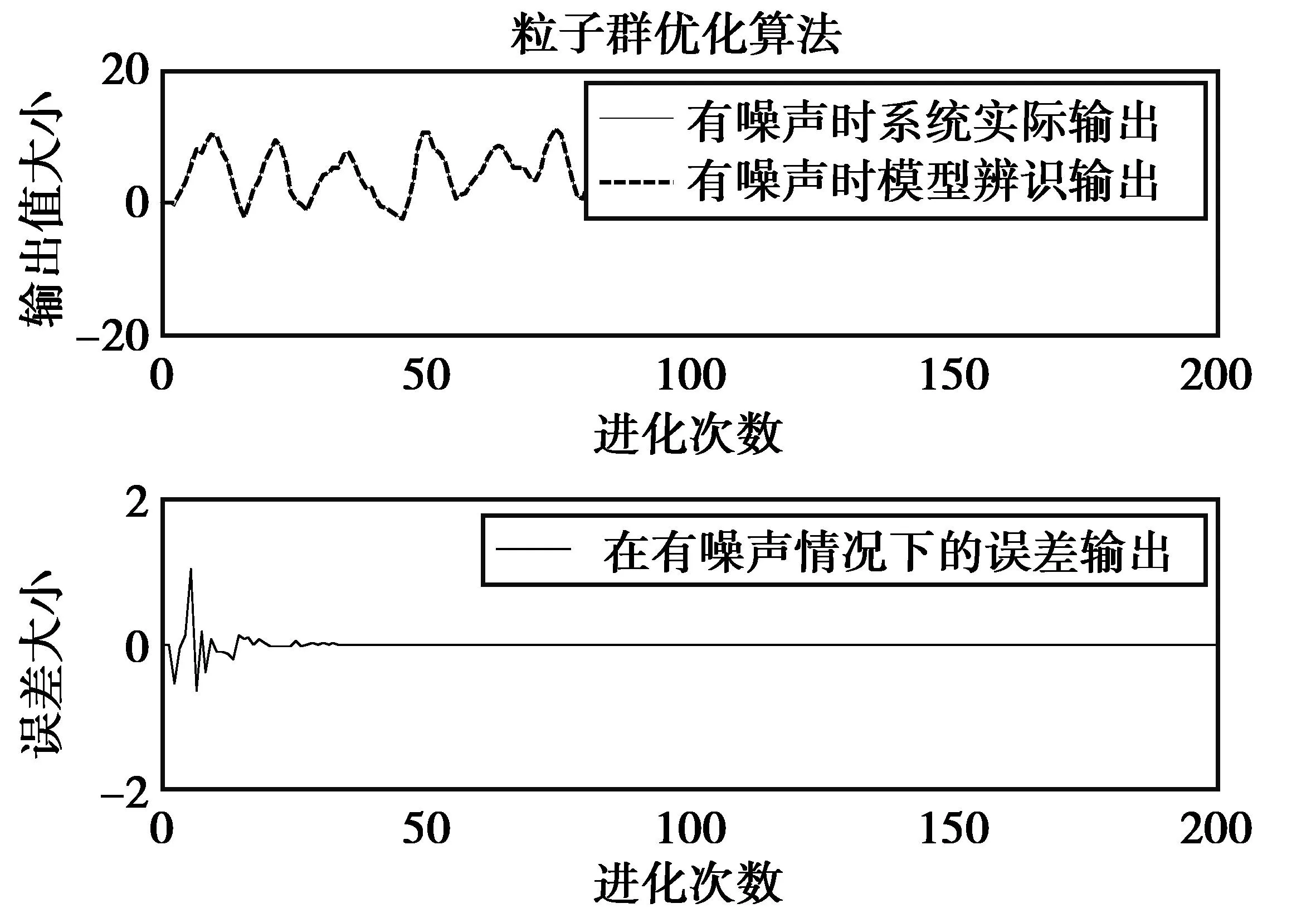
图6　基于粒子群优化算法输出误差图Fig.6　Output deviation chart

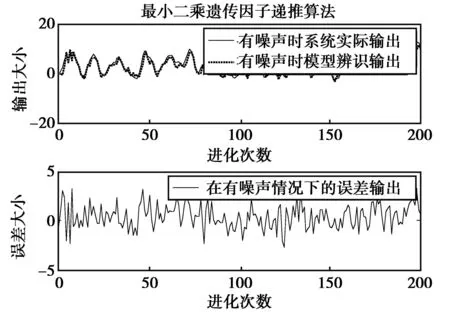
图7　最小二乘遗传递推算法输出误差图[11]Fig.7　Deviation chart of LS genetic dedution algorithm

在图8中是采用的粒子群优化算法的性能函数用Pbest表示，采用最小二乘遗传递推算法性能函数用J表示。性能指标由式(8)来表示。从图8可知，采用粒子群优化的方法，进化次数在5次左右，性能函数就趋于收敛了，而且收敛于8.662 6e-019，它的性能函数的最大值趋于500。而采用最小二乘遗传递推的方法，在进化次数达到20次左右时，性能函数才趋于收敛，收敛于300左右，它的性能函数的最大值达到了4 500多。由此可以得出粒子群的优化算法的收敛性更好，收敛速度也是非常快的。

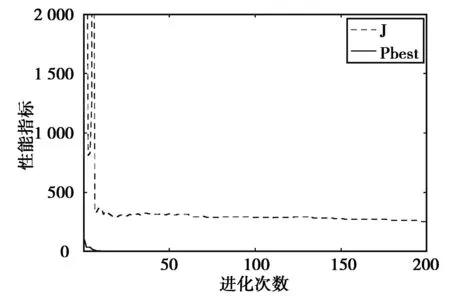
图8　性能指标与进化次数的关系Fig.8　Relation between performance indexand evolution number

4结论

运用MATLAB软件对引用的方法进行仿真实验，比较算法的仿真图与估计的参数值可以看出，PSO方法可以解决系统中参数估计的难题。算法不但可以解决线性动态系统中的参数辨识问题，相比较其他传统算法如仿真试验中引用的最小二乘遗传递推算法，算法的辨识效果更好，不管对于数据的收敛速度还是对于参数的辨识精确度；算法的实现还比较简单，故可以将此算法进一步引用到其他系统中。

参考文献(References)：

[1]刘党辉,蔡远文,苏永芝,等.系统辨识方法及应用[M].北京国防工业出版社,2010

LIU D H,CAI Y W,SU Y Z,et al.The Method and Application of System Identification[M].BeijingNational Defense Industry Press,2010

[2] 陈智勇,张平改,钱艳艳.基于最小二乘法的步态机器人运动轨迹辨识[J].重庆工商大学学报(自然科学版),2014,31(12):43-49

CHEN Z Y,ZHANG P G,QIAN Y Y.Trajectory Identification of Gait Robot Movement Based on Least Square Method [J].J Chongqing Technol Business Univ.(Nat Sci Ed) ,2014,31(12):43-49

[3] 朱呈祥,邹云.基于 PIλDμ控制器的一种线性系统辨识方法研究[J].系统仿真学报,2009,21(12)：3532-3533

ZHU C X,ZOU Y.Identification Algorithm for Linear System Based on Fractional-order PIλDμController[J].Journal of System Simulation,2009,21(12)：3532-3533

[4] 俞林宏,刘庆华.线性系统模态参数识别的递推子空间辨识方法[J].桂林电子科技大学学报,2010,30(6):553-556

YU L H,LIU Q H.Recursive Subspace Identification Method to Estimate Parameters of Linear System[J].Journal of Guilin University of Electronic Technology,2010,30(6):553-556

[5] 程轶平.基于多元线性回归的线性系统状态空间辨识算法[J].北京交通大学学报,2014,38(2)：13-17

CHENG Y P.A State Space Identification Algorithm for Linear Systems Based on Multivariate Linear Regression[J].Journal of Beijng Jiaotong University,2014,38(2)：13-17

[6] 徐晓龙,孙炳楠,付军.基于粒子群优化算法的结构系统辨识[J].科技通报,2007,23(6)：878-884

XU X L,SUN B N,FU J.Identification Method of Structure System Based on Particle Swarm Optimization[J].Bulletin of Science and Technology,2007,23(6)：878-884

[7] GONG M S,TOSHIHIDE K,SUN J.Application of ARX and RARX Methods in Structural Parameter Identification[C]∥2010 Third International Conference on Information and Computing Wuxi,Jiang Su,China,2010

[8] 魏休业,潘宏侠.粒子群优化及智能故障诊断[M].北京:国防工业出版社,2010

WEI X Y,PAN H X.Particle Swarm Optimization and Intelligent Fault Diagnosis [M].BeijingNational Defense Industry Press,2010

[9] KENNEDY J,EBERHART R C.InProc.IEEE International Conference on Neural Networks[J].Particle Swarm Optimi-zation,1995,41：1942 -1948

[10]崔秀美,刘文杰,陈澄.基于最小二乘法的MATLAB辨识仿真实验[J].工业控制计算机,2013,26(7)65-66

CUI X M,LIU W J,CHEN CH.Experiment of MATLAB Identification Simulation Based on Least Squares[J].Industrial Control Computer,2013,26(7)：65-66

[11] HU X,EBERHART R.Solving Constrained Nonlinear Optimization Problems with Particle Swarmoptimization[J].6th World Multiconference on Systemics,Cybernetics and Informatics,Orlando,USA,2002(12)：1188-1191

[12] 侯媛彬,汪梅,王立琦.系统辨识及其MATLAB仿真[M].北京科学出版社,2004

HOU Y B,WANG M,WANG L Q.System Identification and MATLAB Simulation[M].BeijingScience Press,2004

责任编辑：田静

Research on Parameter Identification Method fora Class of Linear System Based on PSO

LI Zhen1, WEI Li-sheng1, CHENG Yun-chang2

(1.School of Electrical Engineering, Anhui Polytechnic University, Anhui Wuhu 241000, China;2.State Grid Huoqiu County Electric Power Supply Co., Ltd, Anhui Liuan 237400, China)

Abstract：This paper studies an accurate identification method for the parameters for a class of linear system, firstly uses PSO (Particle Swarm Optimization) to optimize and iterate the model, chooses suitable deviation standard as the fitness function of the PSO algorithm to iterate the relative parameter speed and size of each particle, on the basis of this, seeks the particle with minimum fitness vale, deducts the optimal fitness function value, implements real-time and accurate estimation of systematic parameters and finally uses experiment to test the accuracy and effectiveness of PSO algorithm based parameter identification method.

Key words：parameter identification; PSO algorithm; criterion function

中图分类号：TP273

文献标志码：A

文章编号：1672-058X(2016)02-0008-06

作者简介：李珍(1989-),女,安徽枞阳人,硕士研究生,从事智能化网络控制理论、系统仿真研究.**通讯作者：魏利胜(1978-),男,安徽巢湖人,副教授,博士,从事嵌入式仪器仪表及系统、智能化网络控制理论、系统仿真研究.E-mail:lshwei_11@163.com.

*基金项目：国家自然科学基金项目(61203033；61172131；61271377).

收稿日期：2015-10-24；修回日期：2015-11-30.

doi:10.16055/j.issn.1672-058X.2016.0002.003