一阶非周期减弱超二次哈密顿系统同宿轨的存在性和多解性*

杨　赛, 陈文雄

(华侨大学 数学科学学院,福建 泉州 362021)



一阶非周期减弱超二次哈密顿系统同宿轨的存在性和多解性*

杨赛, 陈文雄**

(华侨大学 数学科学学院,福建 泉州 362021)

摘要：利用变分方法中强不定泛函的临界点理论得到了非周期一阶哈密顿系统(t)=JHu(t,u)在减弱的超二次条件下同宿轨的存在性和多解性结论.

关键词：一阶哈密顿系统;临界点理论;减弱超二次

1基础知识

主要研究以下非周期超二次的一阶哈密顿系统同宿轨的存在性和多解性：

(1)

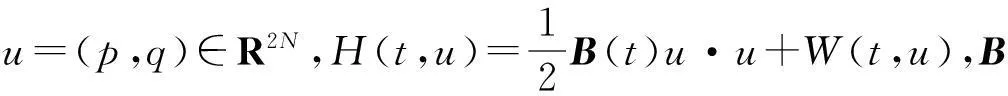
作为动力系统的一个特殊情况,哈密顿系统在研究气体动力学、流体力学、相对论力学和核物理中扮演着重要的角色.在过去的几十年间,一阶哈密顿系统同宿轨的存在性和多解性已经被广泛研究.COTI-ZELATI和EKELAND在文献[1]中首次通过现代变分方法中的临界点理论证明了在满足B是常数矩阵且0∉σ(A),W(t,u)满足凸性条件和Ambrosettti-Rabinowitz超二次条件下，系统(1)同宿轨的存在性.在此之后许多学者通过改进B和W的假设条件得到相似结论.SÉRÉ在文献[2]研究了更一般化的W的假设条件;HOFER和WYSOCKI在文献[3]中利用Fredholm算子和环绕理论研究了W不含凸性条件的情况;文献[4-10]则研究了B和W关于t周期的情况.

当没有周期性假设条件时,最困难的问题是系统(1)在R上的Sobolev嵌入缺乏紧性.DING和JEANJEAN在文献[11]中通过控制W的大小在t无穷远处恢复紧性的方式得到了系统在非周期渐进二次情况下的同宿轨;DING和LEE在文献[12]中通过自治极限方程的方法研究了非周期超二次的情况；ZHANG等在文献[13]中减弱了W的假设条件.

当B是常数矩阵且0是σ(A)的谱隙上的一个边界点时,ZHANG等在文献[14]中通过极限方程的方法研究了当W满足非周期和Ambrosettti-Rabinowitz超二次条件情况下系统(1)同宿轨的存在性和多解性;SUN等在文献[15]中研究了W非周期渐进二次的情况.但是文献[14]中W的条件太强,许多函数无法满足这个条件,所以此处在此条件下通过减弱W的非周期条件来研究系统(1),假设条件如下:

(L1) B是一个2N×2N阶常数矩阵,0∈σ(A)，且存在β>0使得(0,β]∩σ(A)=∅;

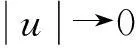
下面是研究的主要结果:

定理1若假设条件(L1)(H1)—(H3)成立,则系统(1)有至少一个同宿轨.

标注1例1的函数满足条件(H1)—(H3).

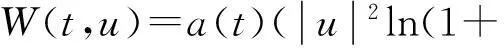
定理2若(L1)(H1)—(H3)成立,且W(t,u)关于u是偶的,则系统(1)有无穷多个同宿轨.

2变分框架的设定

引理1如果(L1)成立,那么σ(A)=σc(A).

证明证明类似参考文献[4]中的Proposition 2.2.

(2)

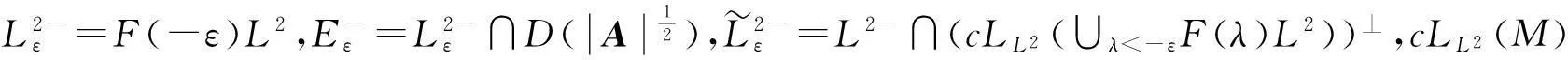
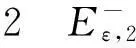
证明证明类似参考文献[4]中的Lemma 2.3.

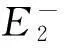
(3)

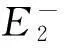
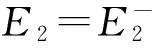
证明证明类似参考文献[15]中的Lemma 2.2.

其中ψ(u)=∫RW(t,u),根据假设条件和引理2可知,φ∈C1(E,R),则φ的临界点即为系统(1)的同宿轨.因此，求系统的同宿轨即转化为求泛函φ(u)的临界点.

3临界点理论

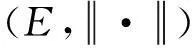
假设X可分自反,S是X*的可数稠密子集,对任意s∈S,定义E上的一个半范数为

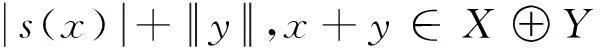
定义τS为其诱导拓扑,w*为E*上的弱拓扑.假设:

(N0) 对于任意的c∈R,φc是τS闭集,且φ′:(φc,τS)→(E*,w*)是连续的;

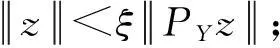
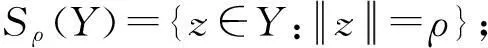
下面的定理分别是T.BARTSCH和DING在文献[16]中Theorem 4.4 和Theorem 4的特殊情况.

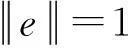
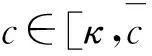
4环绕结构和(Cc)序列

(4)

(5)

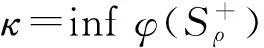
证明根据引理3和式(5)可知,对所有u∈E+和任意ε>0,有

令ε足够小,则∃ρ>0,κ>0,使得φ(u)|∂Bρ∩E+≥0且φ(u)|∂Bρ∩E+≥κ.

(6)

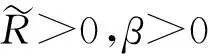
(7)

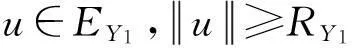
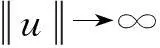
(8)

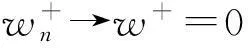
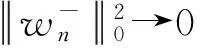
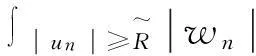
2) 当w+≠0,由式(6)(7)可得

因此存在r>0,使得

(9)

所以：

由式(8)和(9)可知：

结论得证.

引理7若(H1)—(H3)成立,则任意(Cc)序列有界.

证明令{un}⊂E2,则有

(10)

则存在常数c0>0，使得

(11)

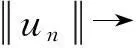
(12)

(13)

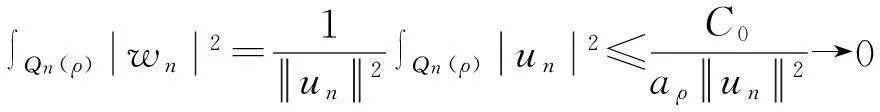
对∀s∈[2,∞),利用Hölder不等式和引理3可知，对∀ρ>0,有

(14)

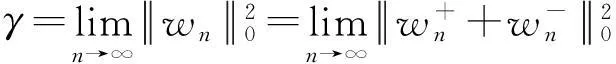
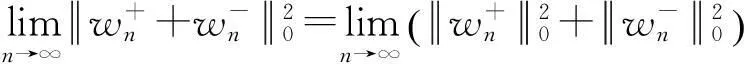
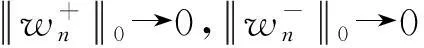
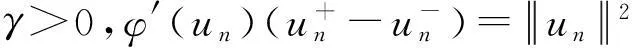
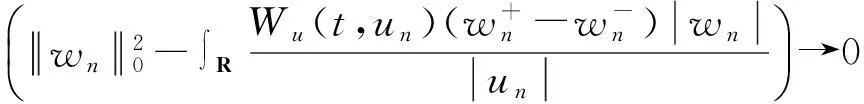
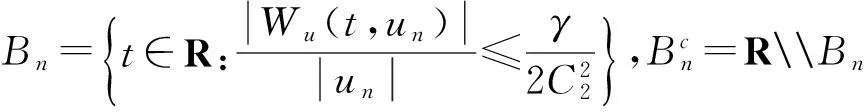
因此:

(15)

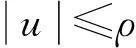
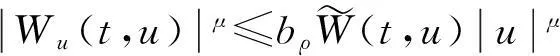
(16)

根据Hölder不等式,式(10)(11)(14)(16)知当n→∞时,有

与式(15)矛盾,结论得证.

引理8在引理7的假设条件下,φ满足(Cc)条件.

证明令{un}⊂E2是(Cc)序列,则只需证明存在收敛子列.由式(4),引理3和引理7，可得

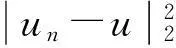
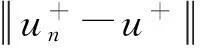
5主要定理的证明

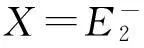
引理9(H1)—(H3)满足时,φ满足(N0).

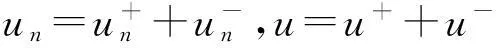
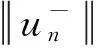
(17)

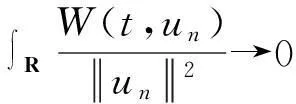
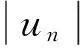
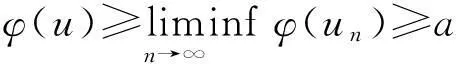
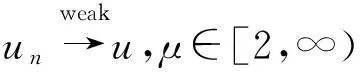
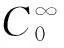
引理10(H1)—(H3)满足时,φ满足(N1).

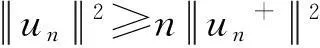
(18)

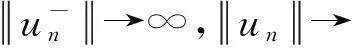
(19)

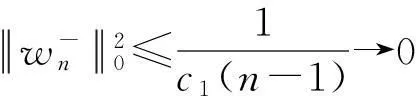
定理1的证明引理9和引理10得到(N0)和(N1),引理4得条件(N2),引理6说明了φ关于定理3的环绕结构,引理7和引理8说明φ满足(Cc)条件.所以由定理3可知φ至少有一个临界点u,使得φ(u)≥κ>0.

参考文献(References)：

[1] COTI-ZELATI V,EKELAND I,SÉRÉ E.A Variational Approach to Homoclinic Orbits in Hamiltonian Systems[J].Math Ann,1990(228):133-160

[2] SÉRÉ E.Existence of Infinitely Many Homoclinic Orbits in Hamiltonian Systems[J].Math Z,1992(209):27-42

[3] HOFER H,WYSOCKI K.First Order Elliptic Systems and the Existence of Homoclinic Orbits in Hamiltonian Systems[J].Math Ann,1990(228):483-503

[4] DING Y H,WILLEM M.Homoclinic Orbits of a Hamiltonian System[J].Z Angew Math Phys,1999(50):759-778

[5] DING Y H,GIRARDI M.Infinitely Many Homoclinic Orbits of a Hamiltonian System with Symmetry[J].Nonlinear Anal,1999(38):391-415

[6] SZULKIN A,ZOU W M.Homoclinic Orbits for Asymptotically Linear Hamiltonian Systems[J].J Funct Anal,2001(187):25-41

[7] DING Y H.Multiple Homoclinics in a Hamiltonian System with Asymptotically or Superlinear Terms[J].Commun Contemp Math,2006(4):453-480

[8] WANG J,XU J,ZHANG F B.Homoclinic Orbits for Superlinear Hamiltonian Systems Without Ambrostti-Rabinowitz Growth Condition[J].Discrete Contin Dyn Syst Ser A,2010(27):1241-1257

[9] WANG J,XU J,ZHANG F B.Infinitely Many Homoclinic Orbits for Superlinear Hamiltonian Systems[J].Topol Met-hods Nonlinear Anal,2012(39):1-22

[10] DING Y H,LI S J.Homoclinic Orbits for First Order Hamiltonian Systems[J].J Math Anal Appl,1995(189):585-601

[11] DING Y H,JEANJEAN L.Homoclinic Orbits for a Nonperi-odic Hamiltonian System[J].J Differential Equations,2007(237):473-490

[12] DING Y H,LEE C.Existence and Exponential Decay of Homoclinics in a Nonperiodic Superquadratic Hamiltonian System[J].J Differential Equations,2009(246):2829-2848

[13] WANG J,ZHANG H,XU J,et al.Existence of Infinitely Many Homoclinic Orbits for Nonperiodic Superquadratic Hamiltonian Systems[J].Nonlinear Analysis,2012(75):4873-4883

[14] DING J,XU J,ZHANG F B.Homoclinic Orbits of Nonperiodic Super Quadratic Hamiltonian System[J].Acta Appl Math,2010(110):1353-1371

[15] SUN J T,CHEN H B,NIETO J J.Homoclinic Orbits for a Class of First-order Nonperiodic Asymptotically Quadratic Hamiltonian Systems with Spectrum Point Zero[J].J Math Anal Appl,2011(378):117-127

[16] BARTSCH T,DING Y H.Deformation Theorems on Non-metrizable Vector Spaces and Applications to Critical Point Theory[J].Math Nachr,2006(279):1-22

责任编辑：李翠薇

Existence and Multiplicity Results for Homoclinic Orbits in First-orderNonperiodic Hamiltonian Systems with Weakened Superquadratic Terms

YANG Sai， CHEN Wen-xiong

(School of Mathematical Sciences,Huaqiao University,Fujian Quanzhou 362021,China)

Abstract：Using the critical points theory for strongly indefinite functionals of variational methods,we can get the existence and multiplicity results of homoclinic orbits for the following first-order nonperiodic Hamiltonian systems (t)=JHu(t,u)with weakened superquadratic condition.

Key words：the first-order Hamiltonian system;critical points theory;weakened superquadratic

中图分类号：O177

文献标志码：A

文章编号：1672-058X(2016)02-0014-07

作者简介：杨赛(1992-),男,江西新余人,硕士研究生,从事非线性泛函分析研究.**通讯作者：陈文雄(1982-),男,福建泉州人,讲师,从事非线性泛函分析研究.

*基金项目：国家自然科学基金(11226115).

收稿日期：2015-06-22；修回日期：2015-07-17.

doi:10.16055/j.issn.1672-058X.2016.0002.004