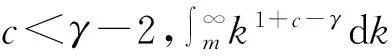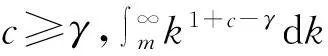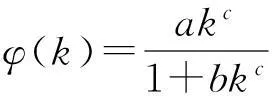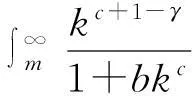具有非线性发生率的森林火灾模型阈值分析*

尹礼寿, 张晋珠

(太原工业学院 理学系,太原 030008)



具有非线性发生率的森林火灾模型阈值分析*

尹礼寿, 张晋珠

(太原工业学院 理学系,太原 030008)

摘要：在具有出生和死亡的一类SIS传染病模型中，考虑了非线性发生率对阈值的影响，对模型进行了改进；主要分析了复杂网络中考虑出生及死亡的情形下非线性率对传染病阈值的影响；结果表明：非线性感染力对传染阈值有着严重影响，传染病阈值λc与因病死亡率β有着非常密切的关系.

关键词：死亡率；非线性发生率；阈值；稳定性

利用数学模型来研究传染病的传播已成为应用数学知识解决实际问题的一个重要领域，已经取得了许多实用价值很高的研究成果[1-3].大部分传染病模型都假设种群个体数量是常数N，实际上有些疾病，出生和死亡(自然死亡、因病死亡等)对种群个体数量的影响是极大的.因此，文献[1]中提出了具有出生和死亡的传染病模型，这对有些疾病的实际传播机制更加贴近，更有实用价值.

即使是考虑了出生和死亡的传染病模型[1]，在对传染病阈值的分析计算中，一般都假设节点的发生率符合“马太效应”，即节点的度越大，感染其他节点的概率就越大，但有些疾病的传播机制与这种假设不符合，一个染病的个体在单位时间内不可能与其所有的邻居节点进行接触(比如性疾病).因此，提出了非线性发生率.

1模型介绍

主要在具有出生与死亡的传染病模型中采用非线性发生率研究传染病模型的动力学性态.

所采用的模型中，考虑个体出生率δ，感染率λ，以及个体的死亡率.假定个体因感染疾病死亡的概率为β.假定ρk(t)为度为k的节点中染病者所占密度、Sk(t)为度为k的节点中易感者所占密度.

基于上述假设，具有出生和死亡的传染病模型(森林模型)为

(1)

其中θ(ρk(t))是指网络中任意一个连接指向一个感染者个体的概率.对于无尺度网络，其具体表达式为

(2)

式(1)中第一个方程的首项代表单位时间内易感者出生的概率，第二项代表感染者个体传染易感者个体的概率，第二个方程第二项代表单位时间内感染者个体因病死亡的概率.

2阈值分析

假设模型(1)中两方程式等于零,得模型(1)的线性近似系统为

两式相加求解得

(3)

(4)

在式(3)(4)的计算中，不是一般性，假设δ=1.为得到关于θ的自适应方程，把式(4)代入式(2)中，求解得

(5)

(6)

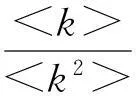
从式(6)求解得阈值

(7)

从而

(8)

3具有非线性发生率下的阈值分析

a) 当c=1,b=0时，φ(k)=ak.在此情形下：

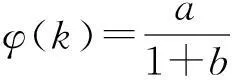
c) 当0

无尺度网络的度分布又具有幂率分布p(k)～k-γ(2<γ<3)的特征，利用积分连续逼近∑kp(k)k1+c来计算λc，得

4结论分析

参考文献(References)：

[1]LIU J Z,TANG Y F,YANG Z R.The Spread of Disease-with Birth and Death on Networks[J].Elsevier Science,2008(9):38-49

[2] 徐芳.具有非线性发生率的传染病模型的研究[D].甘肃：兰州交通大学，2009

XU F.Research of Epidemic Model with Nonlinear Incidence[D].Gansu Province Lanzhou Jiaotong University,2009

[3] ZHANG H F,FU X C.Spreading of Epidemics on Scalefree Networks with Nonlinear Infectivity[J].Nonlinear Analysis，2008(2):353-367

[4] 张旭.含有非线性发生率和治疗项的传染病模型[D].重庆：西南大学，2008

ZHANG X.Epidemic Model with Nonlinear Incidence and Treatment of Items[D].Chongqing:Southwest University,2008

[5] 艾霜.含有时滞的不连续神经网络在非线性干扰下的指数同步[J].重庆工商大学学报(自然科学版)，2015(9)：24-29

AI S.Exponential Synchronization of Delayed Neural Networks with Discontinuous Activations and Nolinear Perturbation[J]. Chongqing Technology and Business University (Natural Science), 2015(9)：24-29

责任编辑：田静

Analysis of Threshold Value of Forest Fire Disaster Modelwith Nonlinear Incidence Rate

YIN Li-shou, ZHANG Jin-zhu

(Department of Science, Taiyuan College of Technology, Shanxi Taiyuan 030008, China)

Abstract：In a class of SIS epidemic model with birth and death, this paper considers the impact of nonlinear incidence rate on threshold value, improves the model, and mainly analyzes the influence of nonlinear rate on the epidemic threshold value based on considering the situation of the birth and death in complex network. Results show that nonlinear infectivity has severe effect on epidemic threshold value and that there is very close relation between epidemic threshold value λc and the death rate β with disease.

Key words：death rate; nonlinear incidence rate; threshold value; stability

中图分类号：O175.3

文献标志码：A

文章编号：1672-058X(2016)02-0005-03

作者简介：尹礼寿(1982-)，男，山西盂县人，讲师，硕士研究生，从事传染病的数学建模与动力学分析理论研究.

*基金项目：山西省教育厅科技研发基金项目(20091041)；太原工业学院理科重点基金项目(2009LZ02).

收稿日期：2015-10-01；修回日期：2015-11-04.

doi:10.16055/j.issn.1672-058X.2016.0002.002