2016年数学高考模拟卷(文科)
2016-05-19骆永明
2016年数学高考模拟卷(文科)
一、选择题:本大题共8个小题,每小题5分,共40分.在每小题给出的4个选项中,只有1项是符合题目要求的.
1.已知集合M={1,2,3,5,7},N={x|x=2k-1,k∈M},则M∩N=()
A.{1,2,3}B.{1,3,5}C.{2,3,5}D.{1,3,5,7}
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
A.3B.4C.6D.7
4.某几何体的三视图如图1所示,其中俯视图中的曲线为半径为2的圆弧,则该几何体的体积为()
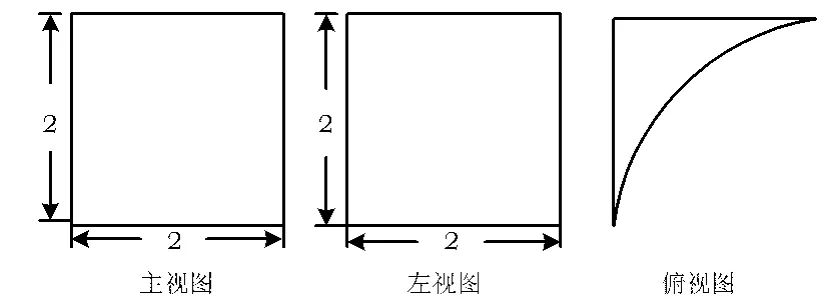
图1
A.6-πB.8-πC.6-2πD.8-2π

6.如图2所示,一个底面半径为R的圆柱被与其底面所成角是30°的平面所截,截面是一个椭圆,则该椭圆的离心率是()

图3

图2
A.只与⊙C的半径有关
B.既与⊙C的半径有关,又与弦AB的长度有关
C.只与弦AB的长度有关
D.是与⊙C的半径和弦AB的长度均无关的定值
8.定义f(x)={x}(其中{x}表示不小于x的最小整数)为“取上整函数”,例如{1.2}=2,{4}=4.“取上整函数”在现实生活中有着广泛的应用,诸如停车收费、出租车收费等都是按照“取上整函数”进行计费的.以下关于“取上整函数”性质的描述,正确的是()
①f(2x)=2f(x);②若f(x)=f(y),则x-y<1;
A.①②B.①③C.②③D.②④
二、填空题:本大题共7小题,第9~12题每空3分,第13~15题每空4分,共36分.
9.双曲线x2-y2=1的离心率为______,渐近线方程是______.
10.设函数f(x)=sinx+cosx,且f(x0)=1,则f(x)的最小正周期为______,sin2x0=______.
12.一个四面体中如果有3条棱两两互相垂直,且垂足不是同一点,这3条棱就象中国武术中的兵器——三节棍,我们把这样的四面体称为三节棍体.若三节棍体ABCD的4个顶点在空间直角坐标系中的坐标分别为A(0,0,0),B(0,2,0),C(4,2,0),D(0,0,2),则|BD |=______,此三节棍体外接球的表面积为______.
13.若正项等比数列{an}满足:a3+a4-a2-a1=5,则a5+a6的最小值为______.
14.当实数x,y满足x2+y2≤1时,|x+3y+a|+|6-x-3y|的取值与x,y均无关,则实数a 的取值范围是______.
15.在给定的直线y=x+t上任取一点P,从点P向圆x2+(y-2)2=8引一条切线,切点为Q.若存在定点M,恒有PM=PQ,则t 的取值范围是______.
三、解答题:本大题共5个小题,共74分.解答应写出文字说明、证明过程或演算步骤.
16.(14分)在△ABC中,角A,B,C所对的边分别为a,b,c,满足
1)求角C;
17.(15分)已知无穷数列{an}分别满足|an+1-an|=2,且a1=1.
1)若数列{an}都为递增数列,求数列{an}的通项公式.
2)若数列{cn}满足:存在唯一的正整数r(其中r∈N*),使得cr+1<cr,称数列{cn}为“梦r数列”.若数列{an}为“梦5数列”,求数列{an}的前n项和Sn.
18.(15分)在如图4所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠ABC=60°,AB=2CB=2.在梯形ACEF中,EF∥AC,且AC=2EF,EC⊥平面ABCD.

图4
1)求证:BC⊥AF;
2)若直线CE与平面ADF所成角为30°,求CE的长.
19.(15分)已知抛物线C的顶点在原点,焦点为F(0,1).
1)求抛物线C的方程;
2)若直线l与抛物线C交于2个不同的点A,B,且弦AB中点M在⊙O:x2+y2=1上,求直线l斜率的取值范围.
20.(15分)设函数f(x)=x|x-a|+b,其中a,b∈R,且a≤1.
2)若函数f(x)在[0,1]上存在零点,求实数b的取值范围.
参考答案
1.B2.A3.D4.D5.A6.B7.C8.C
15.t≤-2或t≥6
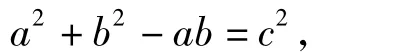


17.解1)数列{an}为递增数列,从而an+1-an=2,故an=2n-1.
2)因为数列{an}满足:存在唯一的正整数r= 5,使得ar+1<ar,且|an+1-an|=2,所以数列{an}必为1,3,5,7,9,7,9,11,…,即前5项为首项为1、公差为2的等差数列,从第6项开始为首项7、公差为2的等差数列,故

18.1)证明∠ABC=60°,AB=2CB=2,由余弦定理知,故∠ACB=90°,即AC⊥BC.因为EC⊥平面ABCD,所以EC⊥BC.又因为EC∩AC=C,所以BC⊥面ACEF,从而BC⊥AF.
2)解如图5所示,取AC的中点G,过点G作GH⊥AD于H,联结FG,FH.在梯形ACEF中,EF∥AC,且AC=2EF,从而
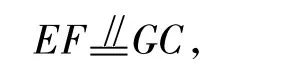

图5
即四边形EFGC是一个平行四边形.因为EC⊥平面ABCD,所以

又因为GH⊥AD,所以

从而∠HFG为直线FG与平面ADF所成角,也即直线CE与平面ADF所成角为∠HFG=30°.
19.解1)由已知得抛物线C的方程为x2=4y.
2)设直线l:y=kx+b,A(x1,y1),B(x2,y2),由
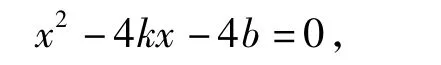
则弦AB中点M(2k,2k2+b)在⊙O:x2+y2=1上,从而

由式(1)和式(2)知

从而k4+4k2-1<0且1-4k2≥0,

2)函数f(x)在[0,1]上存在零点,即x|xa|=-b在x∈[0,1]上有解.令g(x)=x|x-a|,只需-b∈{y|y=g(x),x∈[0,1]}即可.
①当a≤0时,g(x)=x(x-a)=x2-ax在[0,1]上单调递增,从而g(x)∈[0,1-a],即a-1≤b≤0.
②当0<a≤1时,
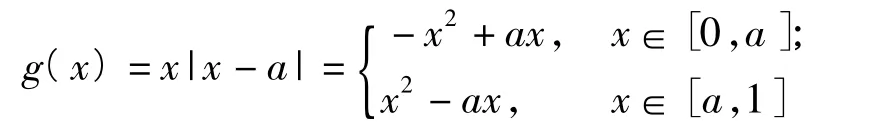
分类讨论解得

供稿人:骆永明(浙江省绍兴市稽山中学)
