基于动态线性步长的分群交替果蝇优化算法研究

胡丽芳，郭　星，2，李　炜，2（.安徽大学　计算智能与信号处理重点实验室，安徽　合肥　230039；2.安徽大学　计算机科学与技术学院，安徽　合肥　23060）



基于动态线性步长的分群交替果蝇优化算法研究

胡丽芳1，郭星1，2，李炜1，2
（1.安徽大学计算智能与信号处理重点实验室，安徽合肥230039；2.安徽大学计算机科学与技术学院，安徽合肥230601）

摘要：本文在传统的果蝇优化算法基础上提出了一种基于动态线性步长的分群交替优化算法.首先利用动态线性步长来控制算法搜索空间的大小，从而平衡了算法寻优的全局性能和局部性能.其次，利用双子群交替策略来解决多峰优化函数容易陷入局部最优的问题.最后，使用了6个经典测试函数来进行实验测试，验证了本文提出的算法具有求值精度高、稳定和收敛速度快等优点.

关键词：演化式计算；果蝇算法；动态线性步长；分群交替

1　果蝇优化算法原理

果蝇优化算法（Fruit Fly Optimization Algorithm, FOA）是由台湾学者潘文超教授在2011年6月份提出的一种基于果蝇觅食行为的演化式全局寻优的新方法[1].该算法将果蝇在觅食过程中的行为进行仿真模拟，利用果蝇对食物味道敏锐的感知能力来快速准确地获取食物.通过计算果蝇群体中每只果蝇所在处的味道浓度判定值，从而得出其相应的味道浓度，求得味道浓度最大的果蝇位置，作为下一次迭代中果蝇群体的出发位置.

基于上述过程，对果蝇觅食行为的进行仿真模拟，FOA算法的推演寻优过程如下：

（1）随机初始化果蝇群体位置，假设果蝇群体的规模为N

（2）果蝇利用嗅觉觅食的随机方向与距离（L为果蝇随机搜索食物的步长[2]）

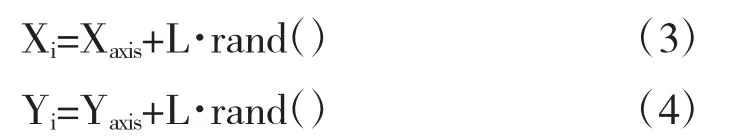
（3）计算群体中每只果蝇的味道浓度判定值，设定每只果蝇的味道浓度判定值为其所在位置与原点的距离之倒数

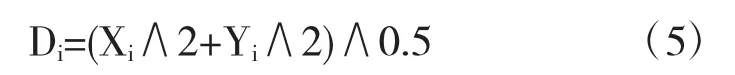
（4）将果蝇的味道浓度判定值代入到适应函数中，求得每只果蝇的味道浓度

（5）获取群体中味道浓度最大的果蝇

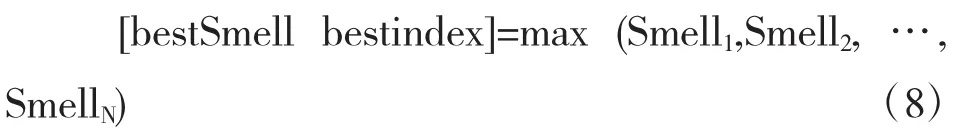
（6）更新果蝇群体位置，所有果蝇飞往味道浓度最大的果蝇所在位置

（7）继续下一轮迭代，重复（2）-（5），并且将每次获取的味道浓度最优值与前一次迭代结果进行比较，如果优于前一次，则执行（6）以更新果蝇群体位置，否则继续迭代，直到达到预先设定的迭代次数结束.

2　果蝇算法优化改进

2.1 FOA的局限性

（1）如上步骤7中所述，FOA在寻优的过程中，如果当次迭代中所获取的群体最大味道浓度值优于前一次迭代的结果，则将果蝇的群体位置更新到此处.可见，影响果蝇群体移动的因素只有前一次迭代的结果[3]，这就大大限制了果蝇群体在搜索过程中位置移动的变化.

（2）果蝇在觅食的过程中，其所在位置是随机产生的，仅用步长L来控制其随机移动的方向和距离.在FOA中，步长L为一个定值，但是如果L设置得太大，虽然增强了全局搜索能力，但同时也降低了局部搜索能力；同理，如果L设置得太小，会增强局部搜索能力同时降低了全局搜索能力[4].另外，步长为一个固定值会导致果蝇的群体位置被限制在一个固定的范围内，对于多峰的情况，很容易陷入局部最优情况无法跳出[5].

2.2基于动态线性步长的分群交替果蝇优化算法（LD-FOA）

（1）动态线性步长控制搜索空间大小

首先，利用线性生成机制来修改果蝇搜索食物过程中每次迭代的搜索步长L，将L设为

其中，L0为步长的初始值，权重参数a用来平衡果蝇全局和局部搜索能力.n为当前的迭代次数，N为最大迭代次数.

从上述公式可以看出，在迭代开始的时候，权重参数a最大，搜索步长也最大.这个时候具有最强的全局搜索能力.随着搜索迭代的进行，权重参数a的值逐渐减小，搜索步长也逐渐减小，全局搜索能力减弱.

（2）利用双子群交替避免局部最优解

虽然线性步长可以控制搜索空间的大小，但是如果适应函数的峰值很多，在迭代后期还是容易陷入局部最优解.为了解决这个问题，利用双子群（A子群和B子群）交替搜索.

从上述公式可以看出，子群A的搜索步长逐渐增大，最初的时候全局搜索能力最强，局部搜索能力最弱，随着迭代的进行，全局搜索能力减弱，局部搜索能力增强；子群B则反之.在迭代的时候，保存上一次迭代中的最优值，如果本次迭代的结果优于上一次的，则子群A或者子群B的群体位置分别取这两个最优值，取值的策略是交替进行.这种方法的优点是，如果子群A的当前步长已经比较小，而此时子群B的当前步长则相反比较大，可以取代子群A，改变其搜索空间，避免其陷入局部最优解的情况.

3　实验结果与分析

3.1实验过程介绍

为验证基于动态线性步长的分群交替果蝇优化算法的寻优效果，选用6个典型的静态函数[6]，如下表所示，对其求解最小值进行模拟，来检测LD-FOA算法的性能.

表1　测试函数

按照LD-FOA算法的步骤，设置果蝇子群A的规模为200，种群B的规模为100，最大迭代次数为1000.迭代结果与相同实验环境下的标准粒子群算法[7]（PSO）、标准的差分进化算法[8]（DE）和LEMS-FOA[9]的结果进行对比[10]，可以得到四种算法在求解精度和收敛速度上的对比情况如下图所示：

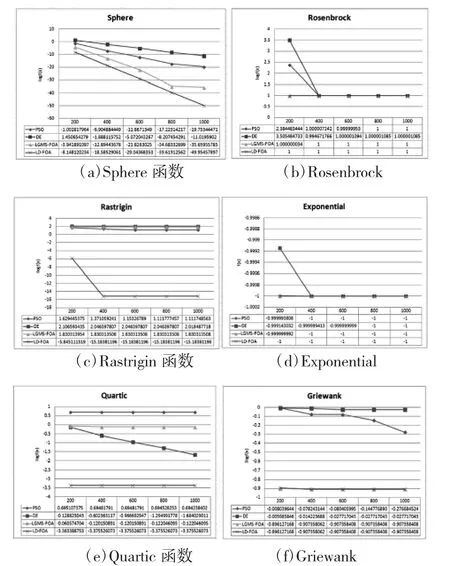
图1　四种算法性能对比

3.2实验结果分析

图1中分别给出了PSO、DE、LGMS-FOA和LD-FOA求解6个测试函数的对比实验结果，从折线图中可以看出，LD-FOA算法在求解精度、收敛速度和稳定性上均由于其它三种算法.在对Sphere函数求解中，LD-FOA的全局搜索性能较好，在对Rastrigin、Quartic、Griewank三个函数的求解中，其它三个函数均陷入局部最优情况没有跳出，而LD-FOA的收敛速度很快，在Rastrigin函数中也较快地跳出了局部极值的情况.

4　结束语

本文提出了一种改进的果蝇优化算法LD-FOA算法.通过使用动态线性的策略来调节步长，从而同时保证了算法寻优的全局性能和局部性能.另外，算法利用双子群交替寻优策略来缓解FOA算法容易陷入局部极值的情况.通过实验证明，LD-FOA算法具有较好的稳定性和收敛速度，并且保证了求值的精度.虽然算法在函数求解最优值的实验中表现出优越性，但在工程问题中的性能还有待于应用验证.

参考文献：

〔1〕胡能发.演化式果蝇算法及其应用研究[J].计算机技术与发展，2013(07).

〔2〕宁剑平,王冰,李洪儒,许葆华.递减步长果蝇优化算法及应用[J].深圳大学学报(理工版)，2014(04).

〔3〕徐富强，陶有田，吕洪升.一种改进的果蝇优化算法[J].苏州大学学报（自然科学版），2014(01).

〔4〕刘成忠,黄高宝,张仁陟,柴强.局部深度搜索的混合果蝇优化算法[J].计算机应用，2014(04).

〔5〕张勇,夏树发,唐冬生.果蝇优化算法对多峰函数求解性能的仿真研究[J].暨南大学学报(自然科学与医学版)，2014(01).

〔6〕张琳,郑忠,高小强.多峰函数优化的混合遗传算法[J].重庆大学学报(自然科学版)，2005(07).

〔7〕唐俊.PSO算法原理及应用[J].计算机技术与发展，2010(02).

〔8〕潘欣,高晓智.基于差分演化的果蝇优化算法[J].微型机与应用，2015(01).

〔9〕Dan Shan, GuoHua Cao, and HongJiang Dong.LGMS -FOA: An Improved Fruit Fly Optimization Algorithm for Solving Optimization Problems,Mathematical Problems in Engineering,2013.

〔10〕吴小文,李擎.果蝇算法和5种群智能算法的寻优性能研究[J].火力与指挥控制，2013(04).

基金项目：安徽省科技攻关项目：有机生猪智能化饲养设备关键技术研究(No.06060701)

收稿日期：2015-12-25

中图分类号：TP18；O221

文献标识码：A

文章编号：1673-260X（2016）04-0021-03