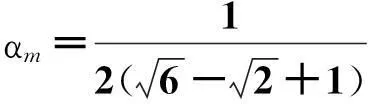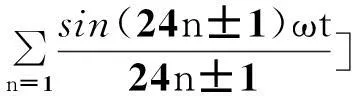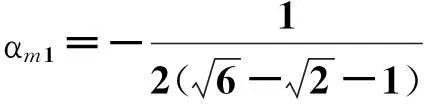多脉波整流器直流侧无源谐波抑制机理研究

高蕾，　孟凡刚，　杨威，　杨世彦

(哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001)



多脉波整流器直流侧无源谐波抑制机理研究

高蕾，孟凡刚，杨威，杨世彦

(哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001)

摘要:为提高多脉波整流器的直流侧无源谐波抑制能力，研究了基于两抽头变换器的24脉波整流器直流侧谐波抑制机理。根据抽头变换器的结构及安匝平衡原理，分析了抽头变换器的功能及工作模式，研究了抽头变换器的工作模式对整流桥输出电流、整流器输入电流及负载电压的影响,给出了抽头变换器变比的理论最优值。理论分析及实验结果表明，抽头变换器的端电压会使其所接的两个二极管交替导通，对整流桥输出电流进行调制，进而产生环流，该环流流经交流侧时会抵消原输入电流中的12k±1(k为奇数)次谐波。另外，抽头变换器所接的两个二极管的交替导通，会在负载上产生附加电压，附加电压的存在可以显著降低负载电压的纹波系数。相应的实验结果验证了理论分析的正确性。

关键词:多脉波整流器； 两抽头变换器； 平衡电抗器； 自耦变压器； 谐波抑制

0引言

多脉波整流技术是大功率整流系统抑制输入电流谐波的主要方法[1-2]。因其具有谐波抑制能力强、系统结构简单、可靠性高等优点，在飞机电源系统、船舶电力系统等领域得到了广泛应用[3]。

在多脉波整流器中，整流脉波数决定着系统的谐波抑制能力[4]。因此，获得尽可能高的整流脉波数是多脉波整流器的设计目标之一。通常来说，提高整流脉波数的方法主要有两种。第一种是增加移相变压器的输出相数，如文献[5-7]中所设计的多相移相变压器。但是，该方法会增加移相变压器结构的复杂性，加大变压器的制造难度；同时，多绕组的交互联结也会降低材料的利用率。在不增加移相变压器结构复杂性的前提下，使用抽头变换器是增加整流脉波数的有效方法[8]。根据抽头数的不同，多抽头变换器通常分为两抽头、三抽头，直至n抽头。以12脉波整流器为例，若使用的抽头变换器抽头数为n，则系统的整流脉波数由12变为12n，因此使用抽头变换器可以显著抑制输入电流谐波[9]。然而，当抽头数的个数达到一定值后，再增加抽头数不仅不能明显降低输入电流THD值，还会增加控制系统的复杂性[10]。在感性负载下，使用两抽头变换器的多脉波整流器的输入电流THD理论值为7.6%。若考虑变压器漏感等实际因素，THD值大约为5%。在大多数场合下，该值满足电网对接入整流器的谐波要求。另外，在众多抽头变换器中，两抽头变换器结构最为简单、可靠。因此，本文以使用两抽头变换器的24脉波整流器为例，分析了抽头变换器的谐波抑制机理，为抽头变换器的应用提供理论指导。

112脉波整流器分析

图1所示为12脉波整流器。

图1中，移相变压器为三角形联结自耦变压器，其等效容量为负载功率的18%左右，可显著降低系统的体积，提高功率密度；零序电流抑制器(zero sequence blocking transformer,ZSBT)可对三倍频电流产生高阻抗，确保两整流桥每个二极管导通120°；平衡电抗器IPR可吸收两整流桥输出电压的瞬时差，使两整流桥能够独立并联工作[11-12]。

图2所示为三角形联结自耦变压器的绕组结构图，图3所示为其相量图。

图2　三角形联结自耦变压器绕组结构图Fig.2　Winding configuration of delta-connected 　　　autotransformer

图3　自耦变压器变压器相量图Fig.3　Phasor diagram of delta-connected 　　　autotransformer

12脉波整流器要求移相变压器输出的两组三相电压存在30°的相位差[13]。根据该要求，图3中α等于15°。因此，图2中自耦变压器绕组匝数满足

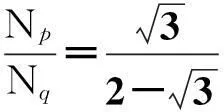
(1)

式中Np和Nq分别为三角形绕组和小绕组的匝数。

根据基尔霍夫电流定律及安匝平衡原理，12脉波整流器的输入电流可以表示为

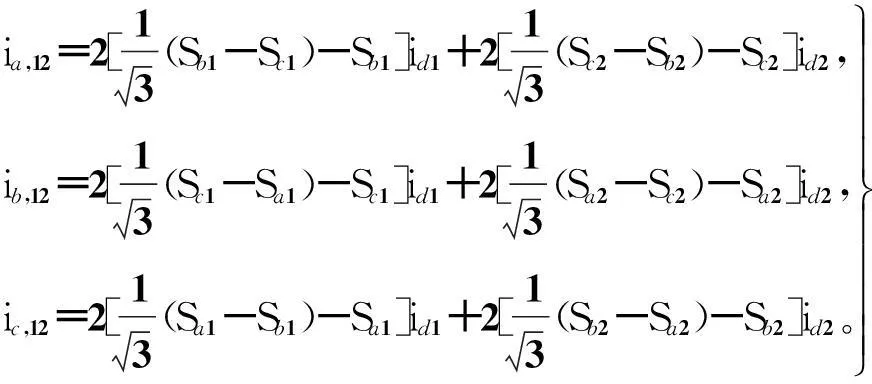
(2)

式中id1和id2分别为两整流桥输出电流；Sa1、Sb1、Sc1、Sa2、Sb2、Sc2,分别为a1、b1、c1、a2、b2、c2相的开关函数。

假设12脉波整流器输入电压为

(3)

则可以得到a1相的开关函数如图4所示。

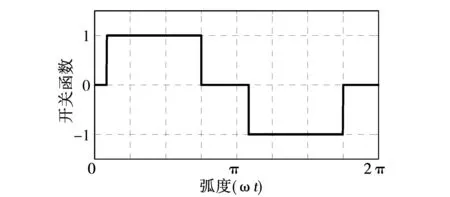
图4　a1相开关函数Fig.4　Switching function of Sa1

各相开关函数之间满足

(4)

在大电感负载下，负载电流可以认为为恒定值，且负载电流与两整流桥输出电流满足

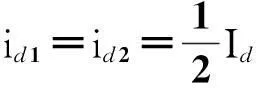
(5)

由式(2)、式(4)和式(5)可以得到

(6)

图5所示为a相输入电流及其谐波频谱。式(7)所示为输入电流的傅里叶级数。由图5和式(7)可知，12脉波整流器输入电流中仅含有12k±1(k为正整数)次谐波，其THD值为15.2%。

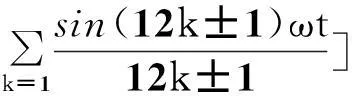
(7)

图5　输入电流及其频谱Fig.5　Input line current of phase a and its spectrum

图1中，假设点m1、m2、m3及m4的电位分别为vm1n、vm2n、vm3n和vm4n， 则负载电压ud,12可以表示为

(8)

即负载电压等于两整流桥输出电压瞬时值的平均值。

根据调制理论，可得两整流桥输出电压满足

(9)

根据图3，自耦变压器输出的两组三相电压满足

(10)

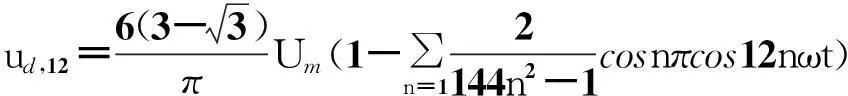
(11)

图6所示为负载电压。负载电压在一个周期内含有12个等宽度的波头，因此图1所示整流器称之为12脉波整流器。

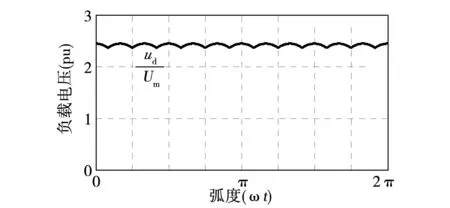
图6　负载电压Fig.6　Load voltage

2抽头变换器的功能及工作模式分析

图7所示为使用两抽头变换器的24脉波整流系统。在多脉波整流系统中，抽头变换器主要有两个作用：一是吸收并联整流桥的输出电压瞬时差，保证各个整流桥能够独立工作；二是产生环流，抵消12脉波整流系统高次谐波。为了便于分析，作以下假设：1)忽略自耦变压器的漏感；2)输入电压为对称的正弦波；3)整流桥为理想器件；4)忽略抽头变换器和自耦变压器的电阻。

由于多脉波整流系统抑制谐波的机理相同，因此下述分析对于使用自耦变压器或隔离变压器的多脉波整流系统皆适用。

图7　使用两抽头变换器的24脉波整流器Fig.7　24-pulse rectifier with double-tapped IPR

2.1抽头变换器的功能分析

2．1．1吸收整流桥输出电压瞬时差

由于两个整流桥的输入电压之间存在30°的相位差，因此两整流桥输出电压的瞬时值不相等。此时，若不加平衡电抗器，则在两个整流桥中，只有瞬时电压较高的二极管导通，因此两组整流桥是轮流工作而不是并联工作。为了使两个整流桥并联独立运行，需要在两个整流桥输出端接平衡电抗器。平衡电抗器的作用是吸收两个整流桥的瞬时值之差，从其中点输出，从而使两个整流桥的输出电压瞬时值相等，保证这两组整流桥同时处于正常整流状态，使负载电流平均分配在两组整流桥中，达到并联工作的目的。

2．1．2产生环流抵消网侧电流谐波

若单纯使用平衡电抗器而不加抽头，则整流系统为12脉波运行，此时网侧电流中含有12k±1(k为正整数)次谐波，与标准正弦波相比存在较为严重的畸变。若使用抽头变换器，则开关管的交替导通会产生流经主整流器电路和抽头变换器所构成回路的环流。理想状态下，该环流可以抵消12k±1(k为正整数)次谐波，使得理想条件下网侧电流存在的最低次谐波为23次。因此，抽头变换器能显著抑制输入电流的畸变。

抽头变换器的上述两个作用相对独立，前者要求抽头变换器在实际运行时有一个临界电感值，保证励磁电流小于每个整流桥输出电流的最小值；后者要求抽头变换器有一个最优变比，在实际运行时能够抵消12k±1(k为正整数)次谐波。因此，临界电感值与最优变比是抽头变换器优化设计的两个重要方面。

2.2抽头变换器工作模式分析

图8所示为两抽头变换器原理图。

图8　两抽头变换器Fig.8　Double-tapped IPR

定义抽头变换器的变比αm为

(12)

根据图7，两抽头变换器的端电压可以表示为

um=vm1n-vm3n-(vm2n-vm4n)=

vm1n-vm2n-(vm3n-vm4n)=

ud1-ud2。

(13)

即抽头变换器端电压等于两整流桥输出电压瞬时值的差。

将式(4)和式(10)代入式(13)，可得两整流桥的输出电压，进而得到抽头变换器的端电压为

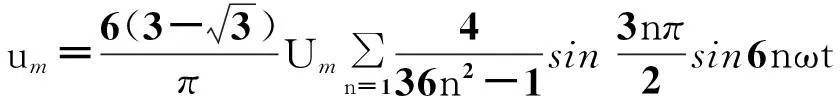
(14)

图9所示为抽头变换器端电压。

图9　抽头变换器端电压Fig.9　Voltage across double-tapped IPR

图8中，当ud1>ud2，即um>0时，二极管Dp导通，根据安匝平衡原理和基尔霍夫电压定理可得

(15)

式中ud,24为使用抽头变换器的24脉波整流系统的负载电压。

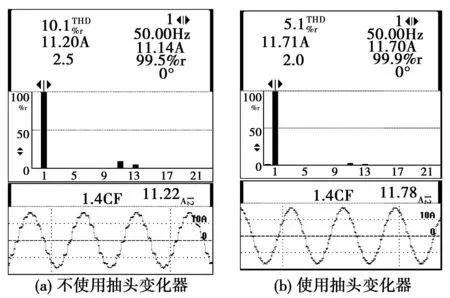
同理，当ud1

(16)

因此，抽头变换器共有两种工作模式。下面分析这两种工作模式对整流器输入电流和负载电压的影响。

3整流器输入电流与负载电压分析

假设Dp和Dq的开关函数分别为Sp和Sq。根据图9，可以得到Sp和Sq满足图10。

图10　二极管Dp和Dq的开关函数Fig.10　Switching functions of Dp and Dq

由式(9)和式(10)及图9可以得到两整流桥输出电流和负载电压满足

(17)

式中：im=(Sp-Sq)αmId，udα=(Sp-Sq)αm(ud1-ud2)。

由式(17)可知，使用抽头变换器后，整流桥输出电流由两部分组成，第一部分为Id/2，该部分与12脉波整流器中整流桥输出电流相等，第二部分为im，该部分称之为环流，它与抽头变换器的变比有关，是抽头变换器在整个系统电流上的附加成分；负载电压也由两部分组成，第一部分ud,12/2为12脉波整流器的负载电压，第二部分um是由抽头变换器产生的附加电压。

3.1抽头变换器对整流器输入电流的影响

下面以a相为例，分析抽头变换器对整流器输入电流的影响。根据式(2)和式(17)，a相输入电流可以表示为

ia,24=ia,12+iam。

(18)

式中

(19)

因此，使用抽头变换器后，整流器输入电流也由两部分组成，第一部分等于12脉波整流器的输入电流，第二部分iam与环流im有关，可以认为是直流侧环流在整流器输入电流中的表现形式。

根据开关函数的表达式，经计算可以得到环流的傅里叶级数为

(20)

将式(7)和式(20)代入式(19)，得到整流器输入电流为

(21)

很显然，抽头变换器的谐波抑制能力与αm相关。为了得到αm的最优值，需计算输入电流的THD表达式。经计算，式(21)中电流的THD表达式为

(22)

为了计算THD的最小值，式(22)中，THD对求αm导数，并令导数等于零，可得

(23)

将式(23)代入式(22)可得THD为7.6%。相比较12脉波整流系统，输入电流谐波得到了显著抑制。图11所示为整流器输入电流及其频谱。

图11　整流器输入电流及其频谱Fig.11　Input line current and its spectrum

将式(23)代入式(21)，得到使用抽头变换器后的整流器输入电流为

(24)

由式(24)可知，使用抽头变换器后，输入电流中不含有12k±1(k为奇数)次谐波，仅含有12k±1(k为偶数)次谐波。也就是说，当抽头变换器的变比满足式(23)时，可以完全抑制输入电流中的12k±1(k为奇数)次谐波。事实上，抽头变换器仅能完全抑制12k±1(k为奇数)次谐波，而不能完全抑制12k±1(k为偶数)次谐波。式(24)中，若要完全抑制输入电流中的12k±1(k为偶数)次谐波，需满足

(25)

即

(26)

式中，αm1小于零。由αm的定义及图8所示的抽头变换器的结构，可以得到αm应满足

0≤αm<0.5。

(27)

显然，式(26)不满足式(27)。因此，不可能使用两个具有不同变比的抽头变换器来抑制输入电流的12k±1(k为正整数)次谐波。

3.2抽头变换器对负载电压的影响

根据式(9)及图10所示的二极管开关函数，得到抽头变换器产生的附加电压

(28)

(29)

图12所示为负载电压。负载电压在一个周期内含有24个等宽度的波头，因此，图7所示整流器在理想条件下可以实现24脉波整流。

图12　负载电压Fig.12　Load voltage

定义直流侧输出电压的纹波系数为

(30)

式中：udmax、udmin和udav分别为负载电压的最大值、最小值和平均值。

对于12脉波整流器，负载电压的最大值、最小值和平均值为

(31)

将式(31)代入式(30)可得12脉波整流系统直流输出电压的脉动系数为0.017 2。

对于使用两抽头变换器的多脉波整流系统，由式(29)可得

(32)

(33)

(34)

同样，为了获得最小纹波系数，分别对式(33)和式(34)中的αm求导，并令导数等于零，得到

(35)

将式(35)代入式(33)或式(34)，可得负载电压的最小脉动系数为4.096×10-3。因此，相对于12脉波整流器，使用抽头变换器的24脉波整流器的负载电压的脉动系数显著减小。

由式(23)和式(35)可知，输入电流THD值最小和负载电压纹波系数最小时，抽头变换器的最优变比相同。

综上所述，基于两抽头变换器的24脉波整流器的直流侧谐波抑制机理可以描述为：抽头变换器所接的两个二极管交替导通，在直流侧可以产生环流；当该环流流经交流侧时，其所含有的12k±1(k为奇数)次谐波与12脉波整流器的输入电流中所含有的12k±1(k为奇数)次谐波幅值相等、相位相反，由此导致输入电流中的12k±1(k为奇数)次谐波得到完全抑制。另外，抽头变换器所接的两个二极管交替导通还会产生一个附加电压，该附加电压与12脉波整流器的负载电压相叠加，共同构成整流器的负载电压，附加电压的存在可以显著降低负载电压的纹波系数。

4实验验证

为了验证上述理论分析的正确性，设计了基于两抽头变换器的24脉波整流器，并进行了相应的实验验证。实验时，为便于设计，抽头变换器变比为0.25；为便于对比，文中同时给出了12脉波整流器的实验结果。实验条件如下：1)输入线电压为250 V；2)负载电阻值为25 Ω，负载电感值为41.2 mH。

图13所示为整流桥输出电流。在感性负载下，不使用抽头变换器时，两整流桥输出电流近似为平滑的直线；使用抽头变换器后，两个二极管交替导通，在整流桥输出电流上叠加了周期为60°的方波。

图13　整流桥输出电流Fig.13　Output current of bridge rectifier

图14所示为抽头变换器端电压，该电压为频率等于300 Hz的三角波，其会使抽头变换器所接的两个二极管交替导通，进而产生环流抑制输入电流谐波。

图14　抽头变换器端电压Fig.14　Voltages across double-tapped IPR

图15所示为流经抽头变换器所接两个二极管的电流。由该图可知，由于抽头变换器端电压的作用，其所接的两个二极管可以实现交替导通。

图15　流经抽头变换器二极管的电流Fig.15　Current through the diodes of double-tapped IPR

图16所示为整流器输入电流及其频谱。未使用抽头变换器时，输入电流THD值为10%左右；使用抽头变换器后，由于环流的作用，THD值为5%左右。由于变压器漏感的影响，整流器输入电流THD值比理论值略小。

图16　多脉波整流器输入电流及频谱(正常工作)Fig.16　Input line currents and their spectrums

图17所示为负载电压。未使用抽头变换器时，负载电压为12脉波，频率为600 Hz；使用抽头变换器后，负载电压频率为1 200 Hz，且纹波较使用前有显著地降低。

图17　负载电压Fig.17　Load voltage

分析上述实验结果可以发现，使用抽头变换器后，整流桥输出电流发生了改变，相当于抽头变换器对整流桥输出电流进行了调制，调制后的电流在输入侧表现为不含12k±1(k为奇数)次谐波。

5结论

针对使用两抽头变换器的多脉波整流器，分析了其谐波抑制机理，主要结论如下：

1)给出了抽头变换器变比的理论最优值。理论分析表明，当输入电流THD值最小时，抽头变换器的最优变比与负载电流纹波系数最小时的最优变比相同。

2)抽头变换器的端电压使其所接的两个二极管交替导通，相当于对整流桥输出电流进行了调制，调制后的电流流经整流器输入侧时，可以抵消12脉波整流器中含有的12k±1(k为奇数)次谐波。

3)两个二极管交替导通产生一个附加电压，该附加电压与12脉波整流器的负载电压相叠加，共同构成整流器的负载电压，附加电压的存在可以显著降低负载电压的纹波系数。

4)本文的分析结果表明，不能使用两个具有不同变比的抽头变换器抑制12脉波整流器输入电流中的全部谐波。

参 考 文 献:

[1]SINGH B,GAIROLA S,SINGH B N,et al.Multi-pulse AC-DC converters for improving power quality: a review [J].IEEE Transactions on Power Electronics,2008,23(1): 260-281.

[2]陆佳政,朱思国,李波,等.特高压输电线路直流融冰变流系统设计[J].电力系统保护与控制,2014,42(11): 124-129.

LU Jiazheng,ZHU Siguo,LI Bo,et al.DC ice-melting converter system design for EHV transmission line [J].Power System Protection and Control,2014,42(11): 124-129.

[3]周宏林,杨耕.用于大型DFIG风电场的混合型HVDC系统中整流器的建模与控制[J].电工技术学报,2012,27(4): 224-232.

ZHOU Honglin,YANG Geng.Modeling and control for rectifier in the hybrid-HVDC system for DFIG-based wind farm [J].Transactions of China Electrotechnical Society,2012,27(4): 224-232.

[4]RODOLFO Castanho Fernandes,PRISCILA da Silva Oliveira,FALCONDES Jos′e Mendes de Seixas.A family of autoconnected transformers for 12- and 18-pulse converters-generalization for delta and wye topologies [J].IEEE Transactions on Power Electronics,2011,26(7): 2065-2078.

[5]KALPANA R,BHUVANESWARI G,SINGH Bhim.Autoconnected-transformer-based 20-pulse AC-DC converter for telecommunication power supply [J].IEEE Transactions on Industrial Electronics,2013,60(10): 4178-4190.

[6]SINGHB,GARG V,and BHUVANESWARI G.A novel T-connected autotransformer-based 18-pulse AC-DC converter for harmonic mitigation in adjustable-speed induction-motor drives [J].IEEE Transactions on Industrial Electronics,2007,54(5): 2500-2511.

[7]张鹏真,陈乾宏,毛浪.一种18脉冲隔离型变压整流器[J].南京航空航天大学学报,2014,46(1): 129-136.

ZHANG Pengzhen,CHEN Qianhong,MAO Lang.A type 18-pulse isolation transformer [J].Journal of Nanjing University of Aeronautics & Astronautics,2014,46(1): 129-136.

[8]PAN Qijun,MA Weiming,LIU Dezhi,et al.A new critical formula and mathematical model of double-tap interphase reactor in a six-phase tap-changer diode rectifier [J].IEEE Transactions on Industrial Electronics,2007,54(1): 479-485.

[9]MENG Fangang,YANG Shiyan,YANG Wei.Modeling for a multitap interphase reactor in a multipulse diode bridge rectifier [J].IEEE Transactions on Power Electronics,2009,24(9): 2171-2177.

[10]孟凡刚,杨世彦,杨威.多脉波整流技术综述 [J].电力自动化设备,2012,32(2): 9-22.

MENG Fangang,YANG Shiyan,YANG Wei.Overview of multi-pulse rectifier technique [J].Electric Power Automation Equipment,2012,32(2): 9-22.

[11]NGUYEN Thanh Hai,LEE Dong-Choon,KIM Chan-Ki.A Series-Connected Topology of a Diode Rectifier and a Voltage-Source Converter for an HVDC Transmission System [J].IEEE Transactions on Power Electronics,2014,29(4): 1579-1584.

[12]张洋,吴旖.用于船舶综合电力推进的同步发电机电磁设计 [J].电工技术学报,2013,28(10): 67-74.

ZHANG Yang,WU Ni.Design of synchronous generator for integrated power propulsion system in marine [J].Transactions of China Electrotechnical Society,2013,28(10):67-74.

[13]PAICED A,Power Electronic Converter Harmonic Multipulse Methods for Clean Power[M].New York: IEEE Press,1996.

(编辑：刘素菊)

Harmonic reduction mechanism at DC link of multi-pulse rectifier

GAO Lei，MENG Fan-gang，YANG Wei，YANG Shi-yan

(School of Electrical Engineering and Automation， Harbin Institute of Technology，Harbin 150001，China)

Abstract:In order to improve the ability of harmonic reduction at DC link of multi-pulse rectifier (MPR),the harmonic reduction mechanism at DC link of 24-pulse rectifier with double-tapped inter-phase reactor (IPR) was analyzed.According to the winding configuration of double-tapped IPR and Ampere-Turn balance,the function and operation mode of double-tapped IPR were analyzed.The effect of operation mode on output currents of the two bridge rectifiers,input current of rectifiers,load voltage were also analyzed,and the theoretical value of turn ratio of IPR was calculated.Theoretical analysis and experimental results show that the conduction in turn of the two diodes connected with IPR will produce a circulating current to modulate the output currents of the bridge rectifiers.When the circulating current flows through the input mains,it reduces the (12k±1)th(k is odd number) harmonics.In addition,conduction in turn of the two diodes produces an additional voltage on the load voltage,which depresses the ripple coefficient of load voltage.Experimental results validate the correctness of theoretical analysis.

Keywords:MPR； double-tapped inter-phase reactor； IPR； autotransformer； harmonic reduction

中图分类号:TM 461.3

文献标志码:A

文章编号:1007-449X(2016)04-0069-09

DOI:10.15938/j.emc.2016.04.010

通讯作者:孟凡刚

作者简介:高蕾(1982—)，女，博士，讲师，研究方向为智能电网及整流系统对电网的影响；孟凡刚(1982—)，男，博士，副教授，研究方向为电能变换及其控制；杨世彦(1962—)，男，博士，教授，研究方向为电能变换及其控制。

基金项目：国家自然科学基金(51307034)；山东省自然科学基金(ZR2013EEQ002)

收稿日期:2014-10-28

杨威(1978—)，男，博士，副教授，研究方向为特种电源变换技术；