初级横向偏移时直线感应电机磁场与推力的有限元分析

吕刚，　曾迪晖，　周桐，　刘志明，　孙守光

(1.北京交通大学 电气工程学院，北京100044；2.北京交通大学 机械与电子控制工程学院，北京 100044)



初级横向偏移时直线感应电机磁场与推力的有限元分析

吕刚1，曾迪晖1，周桐1，刘志明2，孙守光2

(1.北京交通大学 电气工程学院，北京100044；2.北京交通大学 机械与电子控制工程学院，北京 100044)

摘要:由于振动以及弯道等原因，直线感应电机初级和次级经常处于横向偏移状态。考虑在此种工况下，电机拓扑结构和电气结构两个方面均为不对称情况，使用3-D有限元法，分析了直线感应电机的磁场以及推力的变化。首先，给出了直线感应电机的数值计算方法和边界条件，并建立了完整3-D模型来考虑纵/横向边缘效应、初级绕组端部与次级伸出缘等参数。其次，在此3-D模型基础上，计算了不同偏移量时纵/横向的磁场分布，以及讨论了半添槽对直线感应电机出力的影响，提出了纵向和横向磁场的畸变系数，用于量化不对称的程度。最后，计算了推力在对中和横向偏移情况下的变化，并分析了该变化对实际行车中牵引力和控制系统的影响。

关键词:直线感应电机；横向偏移；磁场畸变率；纵向边缘效应；横向边缘效应；三维有限元模型

0引言

在直线电机城市轨道交通中，由于采用直线感应电机后，车辆可以不依赖机械传动系统获取直接驱动力。此种非粘着驱动形式的车辆可以获取高达8%的爬坡能力以及60m的转弯半径。另外，直线感应电机的扁平拓扑结构可以有效降低隧道横断面积从而减少土建工程造价。因此，直线电机车辆能够在不增加制作成本的前提下提升车辆的性能。

直线感应电机的纵向和横向长度的有限性导致了纵向和横向边缘效应，此类效应引起气隙磁场在三维空间的畸变，从而严重影响电机的特性。

初级安装于车下的转向架上，次级铺设在地面。由于车辆运行时的振动以及过弯道的影响，初级与次级之间常会出现横向偏移的现象。在初级与次级横向偏移的情况下，边缘效应会出现更加剧烈的畸变情况，并且由对称转化为不对称，即磁密的畸变将与初级与次级对中时情况不同。本文侧重于研究与计算此种工况下，直线感应电机磁场的变化情况，并引入磁场畸变率进行量化。

2-D有限元法常被用于计算直线感应电机的纵向气隙磁密、推力和法向力[5-6]。但是，由于是默认横向磁密分布均匀并且横向边缘效应常被忽略，因此电机性能的计算结果偏高。2-D有限元法的决定了其无法考虑初级和次级横向偏移的工况，即不可能计算横向磁密分布。等效3-D有限元模型[8]可以用来计算推力和法向力，同时考虑横向边缘效应。等效3-D有限元模型是在假设初级和次级对中的情况下，取直线感应电机一个极的1/2进行计算，因此是1/2极模型。使用该模型可以大大缩短3-D的计算工作量，但是由于忽略纵向边缘效应，因此计算值通常较大，且无法考虑初级横向偏移的情况。3-D整体模型被用于研究不同次级型式对电机性能的影响[9]，同时计算了纵向和横向磁通密度、推力的变化等参量，并据此提出了衡量横向边缘效应的计算公式。但是，该方法所有计算均是在初级和次级对中的前提下进行的，无法考虑直线感应电机在弯道工况时由于初级横向偏移后磁场、力特性的变化。

综上可知，以往的研究集中在初级和次级对中的情况，此种工况对应直线感应电机平稳运行与平直道。但是，对于更加一般的工况，即由于振动和过弯道，导致初级偏移情况研究较少。因为此时直线感应电机的电气与几何出现严重不对称，所以本文通过建立完整的直线感应电机3-D有限元模型，对于整个求解区域，提出了直线感应电机不同组成部分的数值分析方法，计算了横向偏移情况下，纵向磁场分布、横向磁场分布、磁场畸变率等，进一步研究了推力的变化，分析了该变化对实际行车的影响。

1城轨交通中横向偏移的直线感应电机

坐标定义为：x轴为初级运行方向即纵向；y轴为初级铁芯叠片方向即横向；z轴由xy轴确定即法向。直线电机城轨车辆如图1所示，初级悬挂于直线电机车辆下，次级铺设沿线于两条钢轨之间。初级由铁芯和绕组构成，次级由导磁层和导电层构成。当初级由车载逆变器施加幅值和频率都可调的电压时，在初级和次级之间会产生行波磁场，该磁场在纵向边缘和横向边缘都会产生畸变。

图.1　直线电机城轨车辆与直线感应电机 Fig.1　Linear metro system and structure of SLIM

图2中，次级伸出缘(c2) 用来减弱横向边缘效应，c1是初级绕组端部长度。当横向偏移量为 Δy时，次级两侧的伸出缘会由c2变化为c2-Δy和c2+Δy，分别称为伸出缘窄边和宽边。此时，由于伸出缘的宽度变化，气隙磁场将在纵/横向边缘效应的基础上，产生更加强烈的畸变，从而最终影响到电机的性能。

图2　初级和次级横向偏移情况Fig.2　SLIM with lateral displacement

2直线感应电机数值分析

在整个求解区域中，计入次级涡流的电磁方程为：

(1)

其中:v,A,μ,σ,Jp,Js是速度、矢量磁位、磁导率、电导率、初级和次级电流密度。下标x,y,z,i,表示x,y,z分量和求解区编号。其中，求解编号1、2、3、4和5分别为初级铁芯、绕组、气隙、次级铝板和次级铁轭。在每个求解区域，有：

(2)

其中:μCore、μIron和 μ0为初级铁芯、次级铁轭和空气的磁导率。σAl和 σCu为次级铝板和绕组的导电率。求解区域的设为气球边界条件。绕组、初级铁芯、次级铝板、次级钢板等材料之间使用自然边界条件，即为

Ax=Ay=0。

(3)

(4)

令n为次级铝板和次级铁轭的总剖分单元数，则推力为

(5)

Bzj和 Jsyj为第j个剖分单元的磁密z分量和次级涡流y分量。Vj为第 j 个单元体，Te计算周期。

3有限元分析结果

直线感应电机参数见表1。 3-D有限元分析模型如图3所示，切片1#和2#用于获取纵向磁密和横向磁密分布曲线。考虑到初级和次级对中时，偏移量为0mm；当初级和次级产生最大横向偏移时，偏移量为30mm。选取计算条件为：初级电流为210A,频率为5、15、35Hz,Δy=30mm,s=0.25。

表1　直线感应电机参数

图3　3-D整体模型Fig.3　3-D FEM model with displacements

选取频率为5、15、35 Hz,初级电流为 210A,转差率为 0.25，分别计算横向偏移量取0 mm、 30 mm时的纵向磁通密度，如图4中所示。定义不同横向偏移量时，纵向磁场密度的变化率为

(9)

其中，z,f,Δy分别表示磁密 z轴分量、频率、横向偏移量。计算可知，当Δy=30 mm，f=35 Hz时，磁场变化率达到最大值98.16%，可见当初级和次级产生横向偏移后，初级中心线处的纵向磁密变化不大。即在电机铁芯与次级耦合部分，沿纵向的磁密几乎没有变化。

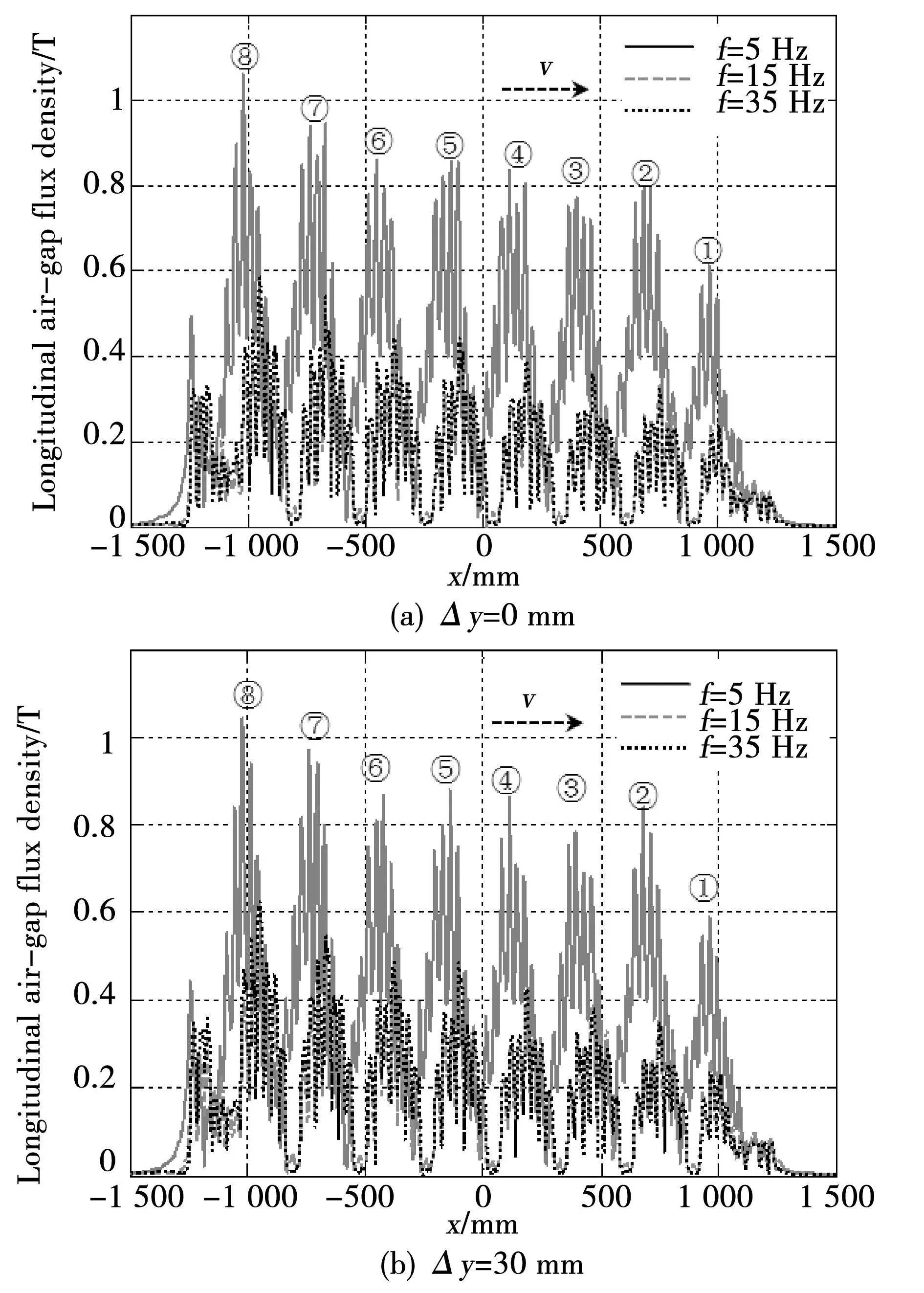
图4　纵向气隙磁密Fig.4　Longitudinal air-gap flux density

由于纵向边缘效应的影响，由图4可见，从第1个磁极第8个磁极，依次消弱。此称之为纵向边缘效应，将减少推力的输出以及产生附加损耗。

如图5所示，标记出的两个区域采用半添槽，本身磁场较弱，同时进口端受到纵向边缘效应磁场消减作用，磁场更加弱，所以进口端的第一个由半添槽绕组产生的磁极几乎对电机出力没有贡献。出口端受到纵向边缘效应磁场增强作用，磁场增大。

图5　入口端和出口端的纵向磁密 Fig.5　Longitudinal air-gap flux density in the two ends

图6　横向气隙磁密Fig.6　Transverse air-gap flux density

不同频率和横向偏移量下，横向气隙磁密如图6所示。图6(a)为初级和次级对中的情况，可见由于横向边缘效应的影响，该磁密曲线呈“U”型，且左右对称。当横向偏移产生后，气隙磁密分布严重不对称，在窄伸出缘区域，气隙磁密急剧增加；而宽伸出缘区域，气隙磁密减少。窄伸出缘区域磁密的增加是因为该部分次级感应板中涡流的减少导致。定义横向磁密的畸变率为

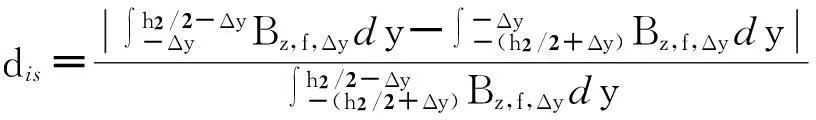
(10)

选取横向偏移量为0、10、20、30 mm，初级电流为210 A,频率分别是5、15、35 Hz ,转差频率0.25，计算横向磁密的畸变率，结果统计如图7所示。

图7　横向磁通分布畸变率Fig.7　Distortion of the transverse flux density

由图可见，随着频率与横向偏移量的增加，横向磁密畸变率处于上升趋势。随着磁场畸变率的上升，由于磁场的分布不均，则推力沿横向的分布将呈左右不对称，易产生附加转矩，影响行车的横向稳定性。同时，由于畸变率较大时，磁场基波含量将降低，则基波推力将减小，同时谐波推力将增加。计算在不同频率下的推力-时间曲线如图8所示。

图8　横向偏移与不同频率时推力变化Fig.8　Variations of thrust with different lateral　　　 displacements

由图8可知，推力在300～400 ms后进入计算稳定。因为在式(5)可知，Bz和Jsy均为正弦量，所以推力稳定后有二倍频波动。当Δy=0 mm,频率为5 Hz、15 Hz、 35 Hz时，推力分别为17 kN、13.6 kN、9.1 kN。当Δy=30 mm时，推力变为15.8 kN、11.7 kN、8.5 kN，且变化率分别为 7%、 13%、6.5%。这一变化主要是由于伸出缘耦合部分磁场变化，以及次级涡流y分量较少导致。

由上述数据可见，列车过弯道时，直线感应电机牵引力会下降，此变化需要在牵引计算以及电机选型时加以考虑，留出适当裕量，否则容易造成牵引力不足。根据上述仿真结果，此裕量考虑在10～15%之间。同时，此工况下由于电机参数产生变化，尤其是互感和次级电阻变化较大，因此对于矢量控制系统来讲，其控制器参数需要重新整定，观测器和定向角计算，需要根据变化的参数做出相应调整。

4结论

本文在不同频率和横向偏移量下，直线感应电机的纵向磁场分布和推力变化，总结为：

1)当初级产生横向偏移后，纵向磁密幅值基本变化不大，相反，横向磁密由原来的对称“U”型变成严重的不对称，具体表现为：窄伸出缘区域磁密增强、宽伸出缘区域磁密减弱。此畸变后的磁密有效值减小，将导致推力减小。

2)由于采用半添槽，直线感应电机进口端和出口端的磁密较弱。进口端受到纵向边缘效应磁场消减作用，磁场更弱，所以进口端的第一个磁极几乎对电机出力没有贡献。因此，在推力计算时，需要着重考虑这种情况，否则容易造成计算值比实际值偏大。

参 考 文 献:

[1]PAI R,BOLDEA I,NASAR S A.A complete equivalent circuit of a linear induction motor with sheet secondary[J].IEEE Trans.Magn.,1988,24(1):639-654.

[2]GIERAS J F,DAWSON G E,EASTHAM A R.A new longitudinal end effect factor for linear induction motors[J].IEEE Trans.Energy Conversion,1987,EC-2(1): 152-159.

[3]LU Qinfen,LI Yanxin,YE Yunyue,et al.Investigation of forces in linear induction motor under different slip frequency for low-speed maglev application[J].IEEE Trans.Energy Conversion,2013,28(1):145-153.

[4]XU W,ZHU J G,ZHANG Y C,et al.An improved equivalent circuit model of a single-sided linear induction motor[J].IEEE Trans.Veh.Technol.,2010,59(5): 2277-2289.

[5]BYUNG J L,DAE H K,YYN H C.Investigation of linear induction motor according to secondary conductor structure[J].IEEE Trans.Magn.,2009,45(6),2839-2842.

[6]QASEER L,MARZOUK R.Hybrid finite-element-boundary element analysis of a single-sided sheet rotor linear induction motor[J].IEEE Trans.Energy Conversion,2014,29(1): 188-195.

[7]ZHANG Yuxing,ZHANG Mingyuan,MA Weiming.Modeling of a double-stator linear induction motor[J].IEEE Trans.Energy Conversion,2012,27( 3):572-579.

[8]SUNG G L,HYUNG W L,SANG H H,et al.Influence of the construction of secondary reaction plate on the transverse edge effect in linear induction motor[J].IEEE Trans.Magn.,2009,45(6): 2815-2818.

[9]NINH V C,KOSEKI T,ISOBE E.Numerical analysis for the influence of the construction of the secondary reaction plate on the characteristics of linear induction motor[J].IECON 2013,2013,pp: 3012-3017.

[10]YAMADA T,FUJISAKI K.Basic characteristic of electromagnetic force in induction heating application of linear induction motor[J].IEEE Trans.Magn.,2008,44(11):4070-4073.

[11]YAMAGUCHI T,KAWASE Y,YOSHIDA M,et al.3-D finite element analysis of a linear induction motor[J].IEEE Trans.Magn.,2001,37(5):3668-3671.

(编辑：贾志超)

Magnetic field and thrust analysis for linear induction motor with lateral displacement

LÜ Gang1,ZENG Di-hui1,ZHOU Tong1,LIU Zhi-ming2，SUN Shou-guang2

(1.School of Electrical Engineering,Beijing Jiaotong University,Beijing 100044,China;2.School of Mechanical,Electronic and Control Engineering，Beijing Jiaotong University,Beijing 100044,China)

Abstract:The single-sides linear induction motor (SLIM) has been applied to the metro vehicle.When the vehicle runs on the turning rails,primary is displaced sideways from a symmetrical position.A full 3-D model,which considering the longitudinal and transverse end effects,overhangs of the primary windings and secondary,as well as lateral displacement,is developed.The air-gap flux densities along longitudinal and transverse direction with different lateral displacements are obtained.Then,influences of half-filled slots on the performance of the SLIM are analyzed,and distortion coefficients of the air gap flux density are proposed to calculate the asymmetry.Finally,thrusts of the SLIM are calculated when the asymmetry between the primary and secondary occurred,and the influence of the thrust variation on the train are debated.

Keywords:linear induction motor；lateral displacement；distortion coefficients；longitudinal end effects；transverse end effects；three dimensional finite-element model

中图分类号:TM 351;TP 273

文献标志码:A

文章编号:1007-449X(2016)04-0064-05

DOI:10.15938/j.emc.2016.04.009

通讯作者:吕刚

作者简介：吕刚(1976—)，男，博士，副教授，博士生导师，研究方向为直线电机分析与控制；

基金项目：国家自然科学基金(51377009，U1134201)

收稿日期:2014-12-16

曾迪晖(1988—)，男，博士研究生，研究方向为直线电机分析与控制；

周桐(1990—)，男，硕士研究生，研究方向为直线电机及设计；

刘志明(1966—)，男，教授，博士生导师，研究方向为机车车辆;

孙守光(1962—)，男，教授，博士生导师，研究方向为机车车辆。