攻克一例,完解一类
2016-05-15浙江省余姚中学龚凤
☉浙江省余姚中学龚凤
攻克一例,完解一类
☉浙江省余姚中学龚凤
在高中平面向量的学习中,经常会遇到以三角形为载体,且涉及一串向量线性和的问题,初次接触,使人会有无从下手的感觉.本文试图通过对典型例题的多种解答,来揭示问题的特点和本质所在,同时找到这类问题的最佳解法.
引例△ABC的面积为12,P为△ABC所在平面内一点,且则△ABP的面积为().
A.3B.4C.6D.9
分析:本题的难点是如何利用所给条件来确定P点的位置,为此,可考虑用坐标法来解决.鉴于本题是选择题,又由题意获知,凡面积为12的三角形,只要符合条件,所得到的△ABP的面积是相等的,因此可构造特殊三角形,以简化解题的运算过程.
解法一:如图1,设△ABC的三个顶点为A(2,0),B(-2,0),C(0,6),又设P(x,y),则=(2-x,-y),=(-2-x,-y),2P—→C=(-2x,12-2y),3=(-12,0).
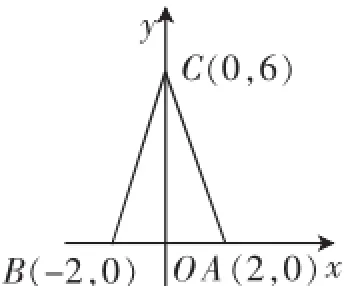
图1

注意到P点的纵坐标为3,故可得△ABP的面积为6.
如果把本题改成证明题或解答题,解法一就不适用了,须采取如下解法.
解法二:不失一般性,如图2,可设A(a,0),B(b,0),C(0,h),又设P(x,y),则
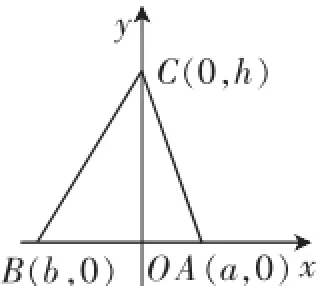
图2
解法二较之解法一,在运算上虽麻烦了一些,但还属于可承受的范围;另外,读者必须明白,当A或B是钝角时,解法二依然是成立的.到此,读者自然会产生这样的一个疑问,不利用坐标法而采用向量法能否解决本题呢?回答是肯定的.

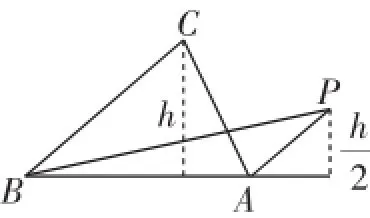
图3
通过对上述问题的解决,不难得到两条经验性的结论:(1)采用坐标法解题的关键是坐标运算的可解性;(2)采用向量法解题的关键是条件等式的化简,从中寻找向量间的关系.因此,为了获得更佳的解法,我们需要在两者之间做一选择,请看下面的例题.
分析:从向量的条件等式入手去解题,似乎有较大困难,故先采用坐标法去求解.
解法一:如图4,设A(a,0),B(b,0),C(0,h),又设P(x,y),则=(x-a,y),2=(2x-2b,2y),=(3x,3y-3h).
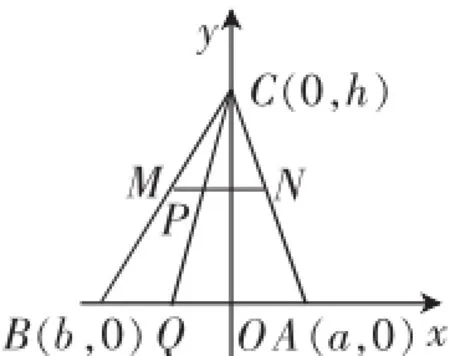
图4

由此可知,点P在中位线MN上,此时已无需深究P点的横坐标,立即可得C—→Q=2m.
然而,若采用向量法去求解,难度会骤然增大,不仅涉及向量的一些新知识,还要依赖于一些平面几何的知识.

由题设知,2(P—→A+P—→B+P—
→C)=P—→A-P—
→C=C—→A,于是得到P—→G=
下面画图.如图5,先画出重心G,再画出P点位置,CP的延长线交边AB于点Q,PG的延长线交边AB于点D.
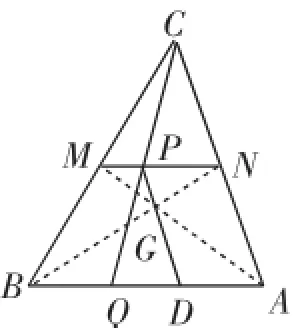
图5
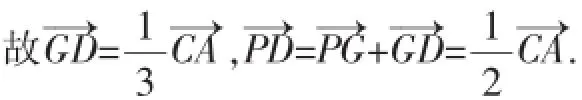
不难看出,如若变动m、n在等式中的位置或变动所求结果,并赋值予m、n,我们就能构造出许多这类问题,有兴趣的读者不妨一试.最后,必须指出,遇到此类问题,坐标法总是可行的,不过当你对条件等式的化简确有把握时,向量法也不失是一种好方法.F
