例析与导数相关的参数问题

☉江苏省海门实验学校刘九华

例析与导数相关的参数问题

☉江苏省海门实验学校刘九华

导数和含参数函数的单调性问题是历年高考命题的热点，也是难点.试题主要有以下两类：一是利用导数解决有关含参数函数的单调性问题；二是已知含参数函数的单调性求参数范围的问题.下面笔者结合平时的教学实践谈谈这两类问题，欢迎指正.

一、利用导数解决含参数函数的单调性问题

利用导数解决含参数函数的单调性问题是常考题型，传统解法要求考生的思维极其严密才能讨论全面.笔者根据教学经验，要解决这类问题，首先明确讨论的三个基本点:1.导函数是否存在零点；2.若导函数存在零点，零点是否在定义域内；3.若导函数有零点，零点是否相等.有时可能是上述几种因素的综合考查，下面举例说明.

①当a＜0时，由f′（x）=0，解得x=a或x=1，a∉（0，+∞），在（0，1）上，f′（x）＜0，在（1，+∞）上，f′（x）＞0，故f（x）的单调递减区间是（0，1），单调递增区间是（1，+∞）.

②当a=0时，f′（x）=x-1，在（0，1）上，f′（x）＜0，在（1，+∞）上，f′（x）＞0，故f（x）的单调递减区间是（0，1），单调递增区间是（1，+∞）.

③当0＜a＜1时，在（0，a）和（1，+∞）上，f′（x）＞0，在（a，1）上f′（x）＜0，故f（x）的单调递增区间是（0，a）和（1，+∞），单调递减区间是（a，1）.

⑤当a＞1时，在区间（0，1）和（a，+∞）上，f′（x）＞0，在区间（1，a）上f′（x）＜0，故f（x）的单调递增区间是（0，1）和（a，+∞），单调递减区间是（1，a）.

综上所述：当a≤0时，f（x）的单调递减区间是（0，1），单调递增区间是（1，+∞）；

当0＜a＜1时，f（x）的单调递增区间是（0，a）和（1，+∞），单调递减区间是（a，1）；

当a=1时，f（x）在（0，+∞）上单调递增；

当a＞1时，f（x）的单调递增区间是（0，1）和（a，+∞），单调递减区间是（1，a）.

点评：此例导函数有零点，但需考虑零点是否落在定义域内与导函数有零点但需要讨论零点是否相等的问题的结合.解题中抓住主要问题，确定分类标准，逐步击破，才能快速、正确地解题.

二、已知函数单调性利用导数求参数范围问题

已知函数单调性，求参数范围是高中数学重点考查的题型之一.关于此类问题在各类高考题中经常出现，变化也多.那么如何简单、准确地解决这类问题呢？一般有以下几种思路可以考虑.

（一）分离参数法

故a的取值范围是a≥3.

点评：若a≥f（x）对x∈D恒成立，则a≥f（x）max；若a≤f（x）对x∈D恒成立，则a≤f（x）min.求函数的最值一般要用到函数的单调性.

（二）数形结合法

例3已知函数f（x）=lnx-a2x2+ax（a∈R）在区间（1，+∞）上是减函数，求实数a的取值范围.

解法1：因为f（x）是区间上（1，+∞）减函数，

所以f′（x）≤0在上（1，+∞）恒成立.

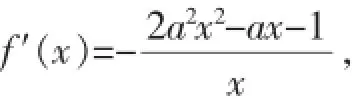
即2a2x2-ax-1≥0在（1，+∞）上恒成立.但此时无法分离参数a，分离参数法不奏效.因为2a2x2-ax-1≥0在（1，+∞）上恒成立，令g（x）=2a2x2-ax-1，

当a=0时，-1＜0，故a=0不满足题意.

当a≠0时，2a2＞0，Δ=9a2＞0.

故由二次函数图像，数形结合知，

（三）分类讨论法

点评：当无法分离参数时，可用分类讨论法求参数的取值范围.但是，若导函数与二次函数有关，用数形结合法能更简便、快速地解决问题，比分类讨论法更方便.

在每年的高考试题中都会出现与函数单调性、导数有关的问题.掌握了以上两种题型及常规处理方法，才能对新颖题型的处理游刃有余，同时能培养学生思维的深刻性和灵活性.G