妙用“类比”激发创新

☉湖北省武汉市第十二中学余智敏☉湖北省武汉市钢城第十四中学何春玲

妙用“类比”激发创新

☉湖北省武汉市第十二中学余智敏☉湖北省武汉市钢城第十四中学何春玲

牛顿说过：“没有大胆的猜想，就做不出伟大的发现.”说明合情推理这种思维方式何其重要！类比就是研究两个对象在某些方面相同或相似的一种思维方式，我们平常碰到的具有探究价值的问题，若能合理联想，将问题一般化、类比、拓展等，则会有新的发现，这就是“再创造”.若能持之以恒，必能激发我们学习数学的兴趣，提升我们的数学素质和探究能力.

本文列举若干用“类比”解题的例子，期望起到抛砖引玉的作用.

图1

证明：如图1，延长AO交BC于点D，以AD为对角线作平行四边形AEDF，则A—→D=A—→E+A—→F，而由平行线分线段成比例定

类比1：设O是△ABC内部的一点，且有O—→A+2O—→B+ 3O—→C=0，则△ABC的面积与△AOC的面积的比为（）.

解析：类比1与问题1完全一样，类比可得，S△BOC∶S△COA∶S△AOB=1∶2∶3，所以S△ABC∶S△AOC=（1+2+3）∶2=6∶2=3.

问题2：求过抛物线y2=2px（p＞0）的焦点F的弦AB的最小值.

解析：如图2，设弦AB的中点为E，分别过点A、E、B作准线的垂线，垂足分别为D、H、C，由抛物线的定义知，|AD|=|AF|，|BC|=|BF|，所以|AB|=|AF|+ |BF|=|AD|+|BC|=2|EH|，由图容易知道|EH|≥|GF|，当且仅当AB与x轴垂直时，|EH|=|GF|，即|AB|min=2|GF|=2p（此时AB为通径）.

图2

解析：类比问题2的解法，可得|AB|=|AF|+|BF|=e|AD|+ e|BC|=2e|EH|，而|EH|≥|GF|，所以当且仅当AB与x轴垂直时，|EH|=|GF|，即|AB|min=2e|GF|=2·

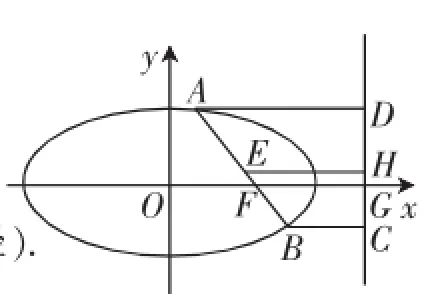
图3

结论2：圆锥曲线通径的长度是焦点弦长度的最小值，相应于抛物线、椭圆、双曲线分别曲线是过焦点与对应的双曲线一支相交的焦点弦）.

解析：由对称性设直线l的方程为y=k（x-c），其中k=

22222

结论3：同一类型的问题有其共同的本质属性和规律，通过类比，揭示出共性，对培养我们思维的广阔性及提高能力大有帮助.实际上，我们可以继续向纵深发散思维，如问题3中的“焦点F”改为“实轴顶点E”；类比4中的“准线与x轴的交点是H”改为“长轴顶点E”等，你又会探索出θ与e有怎样的最简关系式呢？不妨尝试一下.

问题4：求出一个数学问题的正确结论后，将其作为条件之一，提出与原来问题有关的新问题，我们把它称为原来问题的一个“逆向”问题.例如，原来问题是“若正四棱锥底面边长为4，侧棱长为3，求该正四棱锥的体积”.求，它的一个“逆向”问题可以是“若正四棱锥底面边长为4，体侧棱长”；也可以是“若正四棱锥的体积所有侧面面积之和的最小值”.

试给出问题“在平面直角坐标系xOy中，求点P（2，1）到直线3x+4y=0的距离.”的一个有意义的“逆向”问题，并解答你所给出的“逆向”问题.

分析：解答本题的关键是提出问题，理解问题中的条件和结论，条件是一个点P（2，1）、一条直线3x+4y=0、一个关系点P（2，1）与直线3x+4y=0之间的距离；结论只有一个点P（2，1）到直线3x+4y=0的距离是2，从而以关系为桥梁，将点P（2，1）与直线3x+4y=0分别与结论组成条件，提出有意义的“逆向”问题.

类比5：在平面直角坐标系xOy中，求到直线3x+4y=0的距离是2的点的轨迹.

结论4：问题4的提出要求我们对创新定义必须认真阅读，正确理解，如对问题4的“结论作为条件之一”、“与原来问题有关的新问题”、“有意义的‘逆向’问题”等的含义要深刻理解，理解得越深刻，提出的问题越好，思维层次越高，否则，“有意义”的思维层次就差，甚至“没有意义”；另一方面，问题4更重要的意义还在于要求考生“反思学习过程”，就是当求出一个数学问题的正确结论后，要经常回顾、提炼与总结，这是克服“题海战术”的一个重要途径.F