例谈核心素养在向量教学中的呈现

☉江苏省南通市天星湖中学王小丽

例谈核心素养在向量教学中的呈现

☉江苏省南通市天星湖中学王小丽

众所周知，新一轮课程改革正在积极酝酿之中，教育部以浙江、上海作为新一轮课程改革的示范省市，将更为全面的教育推向全国.原东北师大史宁中教授等正着力数学新一轮课程标准的编制，其提出了在中学传统数学教学注重双基三能（基本知识、基本技能、逻辑思维能力、空间想象能力、推理运算能力）的基础上，将更为细致地进行划分，提出了六大核心素养的培养，即数学抽象素养、逻辑推理素养、数学建模素养、直观想象素养、数据处理素养、运算能力素养.这些素养对于一线教师而言，其实并不陌生，可以这么说，在当下数学教学中，教师通过数学问题的解决，对于学生也不断穿插、提炼了上述素养，只是笔者觉得这种提炼还缺乏一定的体系和系统化，因此，课程改革正是需要将这些碎片化的部分整合起来，给出明确的教学目标，让数学教学变得更有导向性，让学生的数学能力和素养变得更为全面.

向量是新课程中较为重要的章节，将向量引入高中数学教学是高等数学与初等数学合理的衔接.从知识来看，向量体现了抽象与形象的结合，如平面向量基本定理和正交分解，向量体现了很多高等数学背景下的建模类型，如极化恒等式；向量体现了工具性的作用，在解决立体几何和平面几何中有着无可比拟的优越性.下文笔者将结合教学案例谈一谈这些核心素养在向量教学中的实施，限于篇幅选择部分素养进行交流.

一、数学建模素养

建模素养是数学实际价值性的体现，是数学最终服务于生活的所在.课程标准一直致力于数学应用价值的推广，在教材中章建跃等编者编写了很多与数学知识相关的应用题，旨在暗示利用数学建模解决问题的重要性，提高学生数学建模的素养.但是与现阶段高考应试有所不同的是，应用题在高考应试中出现的频率较少、难度也较低，因此，广义的建模也不一定是实际问题的模型建立，笔者认为也可以是数学问题本身的本质模型识别、建构，如何将不同的陌生问题建模为熟悉的数学问题求解，也是亟需培养的核心素养.

在向量章节中，向量有很多实际的重要使用模型可供教学总结，如向量中极为重要的三点共线性质：已知O是直线AB外一点，则A、B、P三点共线的充要条件是O—→P=（1-t）.以这一模型为本设计的向量问题，都是为了培养学生将陌生问题转化为熟悉问题的建模素养，值得教师教学探索.

说明：三点共线性质是平面向量基本定理演变的一个非常重要的性质，使用其可以轻快地解决很多向量相关问题，在理解向量、思维开拓上有着极为重要的作用，特别是对于斜交分解有着深刻的认知和理解，因此，将这样重要的性质以单元知识结构的形态存储，以模型的形态置于头脑中，有助于学生建模素养的形成和问题解决的优化.

二、数学抽象素养

抽象素养是数学核心素养的第一要素，这也是高中数学不同于初中数学、小学数学的重要因素.从低龄段非形式化为主的数学知识学习，到高龄段形式化为主的数学知识学习，学生的学习正是不断地从具体形象到抽象转变，这种转变贯穿于高中数学教学的始终，这正是初等数学上升到一定程度的理性总结，向高等数学靠拢的特征渐渐体现出来.笔者以为，从初高中衔接到高中数学新知教学结束，高中数学非形式化的手段更多的是辅助形式化知识学习，不断灌输数学抽象素养的形成，不断总结抽象归纳的重要性.

例2已知a·b=0，向量c满足（c-a）·（c-b）=0，|a-b|= 5，|a-c|=3，则a·c的最大值为_____.

解析：向量有坐标向量和自由向量，学生往往喜欢坐标向量，而惧怕自由向量，原因很简单：坐标向量是以运算为主的正交分解下的运算，而自由向量更多涉及的是联系几何本质、图形化的一种知识，需要更多的思考，相对而言抽象性较坐标向量大，因此抽象理解需要教学更多关注.请学生思考问题，我们发现，大都学生首先对于问题的处理都是一种代数化的想法.

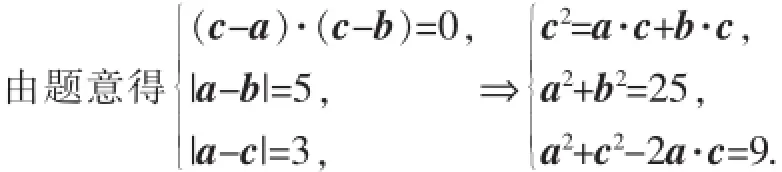
尝试：从向量问题的思维来说，愈来愈多的向量问题是以考查学生思维为主的，如学生所给出的代数法很难在具体运算中得到答案，作为填空题而言缺乏向量抽象的思维是很难实现的.因此，笔者认为，在解决依赖思维作为突破口的向量小题面前，多理解向量的图形本质、多从思维角度入手、多培养抽象的思维，有助于学生掌握中学数学的向量小题，也有助于数学抽象思维的培养和核心素养的建立.仔细分析上述问题，学生给出代数法由于同时还涉及|a|，|b|，|c|，b与c的夹角这些未知数，因此无法求得a·c，而且代数法计算量明显较大，因此选择从思维角度和图形化入手.

导向：引导学生对于本题进行再思考、再精读：“a· b=0”、“（c-a）·（c-b）=0”向我们提供了一个重要的信息：垂直，利用这种垂直关系可以找到本题的图形特征——圆，因此根据题意构造图4.

知识：我们再结合问题进行寻根，问题之根：a·c=|a|·|c|cosθ=（x1， y1）（x2，y2）.

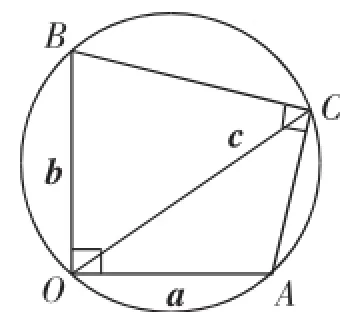
图4

定法：根据求向量数量积的两种不同形式，自然能想到求解此题的两种方法：几何法、解析法（方法之根）；只要我们准确找到了题根，破题在即，跃然纸上，利用多解性的方式将问题给予呈现，也成为了开枝散叶、提高思路的一种方式.

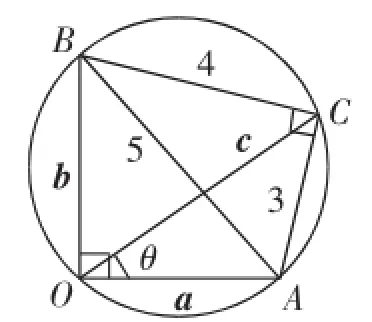
图5

思维素养1：关注到有条件a·b= 0和（c-a）·（c-b）=0，也就是存在两个垂直关系，因此引导学生想到此题中应该蕴含着典型的几何图形，由此可借助于这两个垂直关系去构造图形.如图5，令向量O—→A=a，O—→B=b，O—→C=c，则由a·b=0和（c-a）·（c-b）=0，可得∠AOB=∠ACB=90°，因此可得四边形OACB为圆的内接四边形，AB=|a-b|=5为圆的直径，CA=|a-c|=3，BC=|b-c|=4.记a与c的夹角为θ，在圆中，由θ=平方可得a2+c2-2a·c=9，则a2+c2=9+2|a|·|c|cosθ=9+

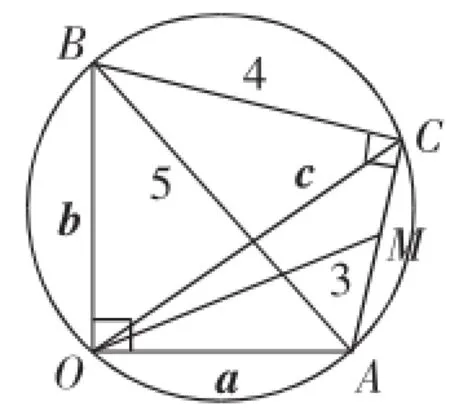
图6

思维素养2：又注意到题中出现了a-c及a·c，因此结合a+c便可得到此三者之间的一恒等关系：a·c=对于a+c，可在△OAC中，取AC中点M（如图6），则a+c=2→，因此，要求a·c的最大值，只需求|的最大值即可.在圆中，由于AC=3，所以当OM经过圆心时取得最大值.18.

说明：从问题解决过程中，我们发现如何将条件一步一步用思维构建成图形，如何利用这些条件在头脑中形成抽象性质的整合是关键，这种利用思维不断解决向量问题的思路是思维素养的核心.另外，在处理数量积c）2］”是一个极为高效的处理工具，教学中可以多加关注和引导.

总之，核心素养还有其余方面的呈现，要适应新的课程教学改革，教师首先要在教学中尝试这些素养的渗透，并注重以知识结合素养进行教学的设计，限于篇幅，笔者未能在逻辑方面、运算方面、数据处理方面等展开叙述，恳请以本文之砖引读者之玉.

1.鲍建生，等.向量教学研究［J］.数学教学，2013（1）.

2.宋卫东.从生“动”到生动，诠释思维品质的提升［J］.中学数学月刊，2013（5）.

3.方厚石.向量教学诠释思维品质［J］.数学通讯，2014（1）.F