一次类比思想使用的复习教学设计
2016-05-15江苏如皋市第一中学夏隽
☉江苏如皋市第一中学夏隽
一次类比思想使用的复习教学设计
☉江苏如皋市第一中学夏隽
众所周知,数学思想教学是中学数学中最为高层次的意识形态的教学,从基本知识、基本技能到知识之间的整合教学,数学教学一直呈现一种螺旋式上升的过程,当知识间整合教学完成之后,教学又进入一种全新的上升状态,即思想方法教学.谈起数学思想方法,学生从初中开始就接触过很多,比如:数形结合思想、分类讨论思想、函数与方程思想等,这些思想方法都很重要,帮助学生在不同问题间游刃有余、轻松解决.笔者请学生数过他们了解的一些数学思想方法,学生可以说出很多思想方法的名称,除上述之外还有特殊和一般的思想、转化与化归的思想、类比思想等,笔者又问这些思想方法间有什么差别?学生一脸茫然.这说明学生并没有真正地体会数学思想的重要作用,他们会将方x+b仅有一解时b的范围用画图的方式求出来,就认为已经掌握了数形结合思想.
其实,思想方法本身也有不同的差别,如函数与方程思想、数形结合思想、分类讨论思想等可以称之为具备知识基础的知识型思想方法,比如:类比思想、转化与化归思想等明显是置身于意识形态中的更为高端的思想方法,其往往除具备知识外,还极大地引领、开拓学生的思维,这就与课程标准对于思想方法渗透于数学教学的描述不谋而合.从现阶段中学数学教学来看,类比思想是启发学生思维发展、延伸,帮助其培养创新性思维较好的方法.笔者以解析几何中圆与椭圆的相似问题做一番设计,从圆的角度出发,来探索如何利用类比思想解决椭圆问题,以笔者之砖引读者之玉.
大家知道,圆和椭圆有着很多类似的性质,比如:类似的形态、直线与其位置关系仅有三种,切线的方程极为相似等,这种相似是偶然的吗?笔者和大家一起来探索这样的问题.
设计一、类比伸缩的认识
先介绍下纵向伸缩变换:将圆x2+y2=a2在纵向均匀压缩为原来的倍,其表达式变为新的曲线,即椭圆= 1(a>b>0),考虑到焦点在y轴的情况类似,故本文只研究焦点在x轴的情形.记:已知圆上点P(x,y)变换成点P′(x′,y′),纵向变换然这是一个一一映射(可逆的),且由于点P、P′的横坐标相等,因此PP′的连线必垂直x轴.同理:有横向伸缩变换.
设计二、类比伸缩的性质
先给出几个类比伸缩的性质:
性质1:记一个变换为f:其将一条直线变换为另一条直线,则变换后直线斜率为原来直线斜率的倍.
说明:由此可知,若两直线原来位置关系为平行,则变换后两直线平行性保持不变.
性质2:记一个变换为f:将线段AB分为比值λ的点P变换成分线段A′B′为同一分比的点P′.
说明:这个容易证明,在伸缩变换中这个比值是不变的,可以利用定比分点公式证明,此处简化.
性质3:一个面积为S的三角形经f变换后的三角形面积S′=S.
简证:设△A1A2A3三个顶点的坐标分别为Ai(xi,yi),则xi=x′i,yi=y′i(i=1,2,3).

说明:对于三角形成立的上述性质,在多边形中也能成立,即可以将多边形分解为多个三角形,即变换前
设计三、类比伸缩的运用
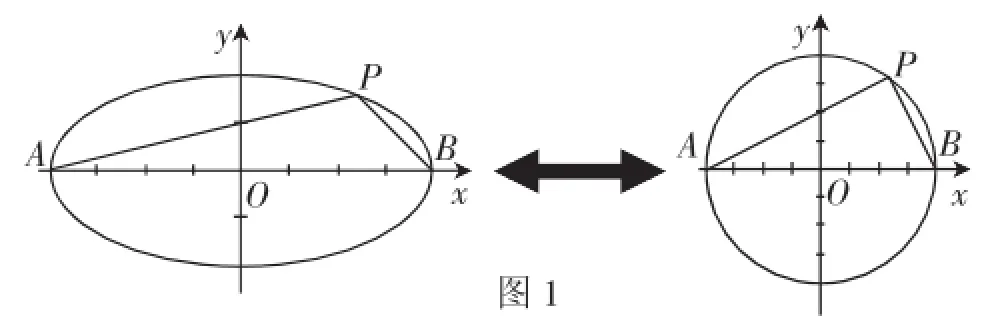
图1
解析:我们可以想象,若本题的背景是圆,则显然有KAP·KBP=-1,因此可以肯定经过了伸缩变换,在椭圆背景定值.如图1,把纵坐标变换为原来椭圆变成半径为a的圆,由性质1得定值.(本性质可以在椭圆中进行证明,但是运算量比通过伸缩变换证明稍显复杂一些)
问题2:(2009年安徽高考数学理科第20题)点P(x0, y0)在椭圆(a>b>0)上,x0=acosβ,y0=bsinβ直线l与直线垂直,O为坐标原2点,直线OP的倾斜角为α,直线l2的倾斜角为γ.求证:点P
分析:问题的实质就是证明直线l1是椭圆在点P的切线方程.由过圆x2+y2=a2上一点(x0,y0)的切线方程为x0x+ y0y=a2,可知利用伸缩变换得到直线l1:=1,即为过点P的椭圆切线.
证明:把纵坐标变换为原来的a倍,则椭圆变成半b径为a的圆,则过圆上点Q(X0,Y0)(Q为P的一一对应点)的切线方程为X0x+Y0y=a2,由伸缩变换因此,l1就是椭圆在点P的切线方程,结论成立.
说明:大家知道,过圆上一点作的切线方程与过圆外一点引两切线,两切点连线的方程都是同一结论,而将背景改变为椭圆后,其实椭圆中也有类似的结论.对于椭圆中相关切线的证明,可以利用类比思想和伸缩变换,这种方式非常有助于学生从不同的视角看待问题,其并没有运用一味的运算方式,而是将圆中现成的结论通过伸缩变换直接转换成椭圆的切线结论,是既高效又简捷的方式,还充满了创新的精神.
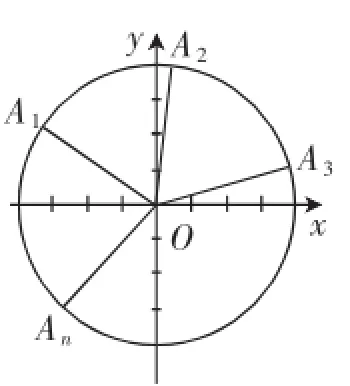
图2
记∠AiOAi+1=θi(1≤i≤n-1),式为琴生不等式,因为f(θ)= sinθ在(0,π)上为凸函数,由琴声不等等号成立,由性质3知,椭圆的内接n边形的面为椭圆内接n边形面积的最大值.
对圆和椭圆之间的类比问题解决,笔者初步做了一番上述的探索.类比思想在其中起到了很大的作用,很多以前看似较为困难的问题在类比思想的运用下,简化了很多,也给我们解决椭圆中类似的问题带来了全新的解决思路.笔者这一课的教学设计对于思维活跃的学生有着比较好的提高,因此,在教学中若能有效结合常规解决方案和类比思想下的伸缩变换,有助于这些优秀学生更好地开拓新的问题解决视角.
圆锥曲线本身就是一个统一体,为了方便中学生学习,我们人为地将其分成了圆、椭圆、双曲线、抛物线四部分.圆和椭圆有着极为相似的性质和特点,笔者建议在学习椭圆过程中,恰如其分地引入圆中的一些性质、特点,利用圆中问题的解决进而伸缩变换解决椭圆中类似的问题,既简化了问题解决的过程,又开拓了学生问题解决的思路,增加了学生的视野,也有利于学生创新精神的培养.
1.张琴竽.活用伸缩变换巧解椭圆问题[J].中国数学教育(高中版),2009(10).
2.刘瑞美.对2009年高考中一道圆锥曲线问题的探究[J].中学数学杂志(高中版),2009(6).F
