基于ARIMA—GARCH模型对上海银行间隔夜拆放利率的实证分析

夏若雯 程宇

[摘要]通过以上海银行间隔夜拆放利率为研究对象，选取2015年1月4日至2015年12月28日的数据作为样本数据，通过Evieas软件分别建立ARM A模型和ARMA-GARCH模型对2015年12月29日至2015年12月31日的上海银行间隔夜拆放利率进行分析，以期望为金融产品的定价和投资套利提供参考。研究结果表明：AR IMA （2，2，1）-6AR（H（1，0）-GED模型相较于ARIMA （2，2，1）模型很好地消除了AR（H效应，并且能够更好地对上海银行间隔夜拆放利率作出短期预测。

[关键词]上海；银行间隔夜拆放利率；ARIMA-6ARCH 模型；短期预测；实证分析

[中图分类号]F470 [文献标识码]A

引言

上海银行间同业拆放利率（简称Shibor）是由信用等级较高的银行组成报价团自主报出的人民币同业拆出利率计算得出的算术平均利率。公布的Shibor品种共有8种，分别是：0N、1W、2W、1M、3M、6M、9M和1Y。Shibor是我国从2007年开始培育的准基准利率，随着利率市场化的发展趋势，Shibor真正成为中国的基准利率也指日可待。随着Shibor的发展与完善，市场上已经有越来越多的金融产品与Shbor挂钩，所以对Shibor走势的预测无论对于金融产品的定价，还是对于投资套利都起着极为重要的作用。

一、文献综述

目前我国国内关于同业拆放利率的研究大致可以分为两类：

第一类是关于同业拆放利率影响因素的实证研究，如崔海亮和徐枫（2007）通过ARIM A模型和Granger因果检验研究发现：一年期人民币银行存款利率和回购利率是影响中国银行系统的同业拆借市场利率（CH IBOR）的主要因素。高柳、田敏（2011）从货币市场资金供求货币流动性比例、金融机构存贷比、法定存款准备金率）、同业拆借替代融资渠道（中央银行再贷款利率、债券回购利率、金融机构存款利率）、拆借行为动机（股票市场价格、房地产市场相关指标、企业短期资金拆借）三个角度分别对影响我国同业拆借利率的因素进行了分析。

第二类是关于对同业拆放利率预测的研究，如彭化非、任兆璋（2005）分别建立了AR IM A和6AR（H模型对隔夜同业拆借利率进行了预测，比较发现ARIMA模型的预测效果比6ARCH模型要好；冯科、王德全（2009）通过建立ARMA-GAR CH模型对同业拆借利率的动态特性进行了刻画，而且通过VaR方法有效地预测出同业拆借利率风险并得出结论7天拆借模型的预测能力优于隔夜拆借模型。

本文沿用第二类研究的思路，旨在通过对同业拆放利率的预测，为金融市场上对金融产品的定价和投资者的套利操作提供参考。

二、ARM A模型的建模思路

自回归移动平均模型ARMA （p，q）由p阶自回归模型AR（p）和q阶移动平均模型MA（q）组合而成，其表达式如下：

运用A RM A模型进行预测分析的思路如下：

（1）检验时间序列是否平稳。常用的方法有通过自相关图判断和单位根检验（ADF检验）。如果时间序列是平稳的，那它的自相关系数就会在滞后阶数大于2或3时很快地趋于零，反之，则序列是非平稳的。不过由于通过自相关图判断具有一定的主观性，所以更经常采用的检验时间序列是否平稳的方法是单位根检验，若得到的ADF的值同时小于1%、5%、10%三个检验水平下的临界值，则拒绝原假设，即时间序列是平稳序列.反之，则序列是非平稳的。

（2）非平稳序列的平稳化。通过步骤（1）如果发现所选序列为非平稳的，则需要通过一定的方法将非平稳序列转化为平稳序列，因为使用ARM A模型对时间序列进行预测的很重要的一个前提便是要求序列是平稳的。事实上，生活中大部分的时间序列都不满足平稳性的要求。常用的将非平稳序列平稳化的方法是差分法。差分自回归移动平均模型ARIM（p，d，q）就是指通过d阶差分将非平稳序列平稳化后构建的ARM A模型。

（3）定阶。根据自相关、偏自相关图同时结合A lC、SC信息准则来对模型定阶，定阶规则如表1所示。

（4）参数估计。运用最小二乘法（OLS）对模型进行估计，由估计结果可初步确定模型。

（5）模型检验。对模型的残差序列进行白噪声检验，如果残差序列出现白噪声过程，则说明我们对于信息的提取已经足够充分，再无信息可以提取了相反，如果残差序列不是白噪声过程，则需要重新调整模型。在实际检验中，主要是检验残差序列是否存在自相关，可用QLB统计量进行2检验，当伴随概率都大于0.05，自相关系数都落在临界区域内，可以认为残差序列是白噪声过程。

三、6 ARCH模型介绍

为了解决金融时间序列变量相关模型的残差序列的异方差性，出现了自回归条件异方差模型ARCH（p）和广义自回归条件异方差模型GARCH（q，p）。

ARCH模型是最简单的条件异方差模型，其核心思想是，误差项在时刻t的方差依赖于时刻t-1的误差平方的大小。AR（H（p）过程的表达式为：

此外，为了更精确地描述时间序列分布的尾部特征，还需要对误差项u_t的分布进行假设。GARCH模型中的残差的分布，一般会有正态（高斯）分布、学生t分布和广义误差分布（GED）3种分布。同ARCH模型一样，6AR CH模型常常使用极大似然估计法进行估计。

四、实证分析

（一）数据选取

选取2015年1月4日至2015年12月28日的上海银行间隔夜拆放利率共246个数据作为样本数据，2015年12月29日至2015年12月31日的数据作为预测比较数据，数据来源于http：∥www.shibor.org/。

（二）构建ARM A模型

5.2.1序列的平稳性检验及非平稳序列的平稳化

1.序列平稳性的图示判断

如图1所示，用时序图描绘样本数据后发现有明显的上升和下降趋势，由此初步判断该序列为非平稳的。

下面通过自相关图和偏自相关图进一步进行分析。如表2所示，由于原序列的自相关函数在延迟36阶的过程中，没有迅速向零趋近的趋势，这说明该序列是非平稳序列。

由于原序列非平稳，考虑将原序列取对数后再次检验平稳性，发现平稳性仍然无法满足，接着对取对数后的时间序列做一阶差分得到取对数后一阶差分条件下的相关图，发现所得序列仍非平稳，再将对数序列二阶差分后得到的相关性检验（表3），发现自相关图迅速趋于零，说明取对数后的二阶差分序列为平稳序列。

2.序列平稳性的单位根检验

由于序列平稳性的图示判断是通过人的肉眼观察判断得出的，因此具有一定的主观性，下面我们采用较为客观和常用的单位根检验（ADF检验）。原序列、取对数后序列、取对数后一阶差分序列、取对数后二阶差分序列的AD F值分别为∶-1.635918、-1.641883、-2.960225、-9.285977。不同检验水平下的临界值为1%∶-3.997418；5%∶-3.428981；10%∶-3.137946，根据ADF检验结果可以发现，原序列、取对数后序列、取对数后一阶差分序列的ADF值都大于不同检验水平的三个临界值，所以不能拒绝原假设；而取对数后二阶差分序列同时小于不同检验水平的三个临界值，所以拒绝原假设，即取对数后的二阶差分序列为平稳序列。结论与序列平稳性的图示判断一致。

5.2.2ARMA模型的定阶、参数估计与检验

结合表3取对数后二阶差分条件下的相关图以及表1ARMA模型的定阶规则，我们初步选定MA（1）、ARIMA（1，2，1）、AR IMA（2，2，1）、AR（IMA（3，2，1）四个模型分别进行参数估计和预测（表4）。由于在参数估计过程中发现常数项始终不显著，所以剔除常数项。

（三）构建ARIM A-6AR（H模型

1.ARCH效应检验

如图2所示，对ARIM A（2，2，1）模型的残差序列用时序图描绘后发现其出现“成群”现象，所以考虑可能存在条件异方差性，因此检验ARIMA （2，2，1）模型的残差是否具有ARCH效应，检验一个模型的残差是否具有AR CH效应通常有两种方法：ARCH-LM检验和残差平方相关图检验。

（1）ARCH-LM检验

对AR IMA （2，2，1）模型的残差进行滞后阶数为3的ARCH-LM检验，结果如表5所示。由于P值为O，所以拒绝原假设，ARIMA （2，2，1）模型的残差序列存在ARCH效应。

（2）残差平方相关图检验

通过Eviews软件得到ARIM（2，2，1）模型的残差平方相关图，结果如表6所示。由于AC和PAC显著不为O，Q统计量又非常显著，所以ARIMA（2，2，1）模型的残差序列存在ARCH效应。

2IAR IM A-GAR CH模型形式的确定

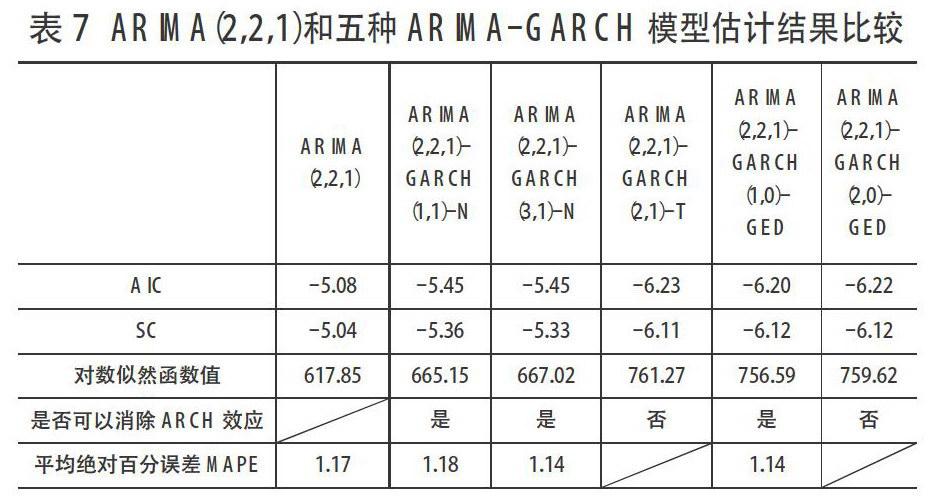
通过反复测算，分别考虑了方程的误差在正态（高斯）分布、学生t分布和广义误差分布（GED）三种不同分布下的不同形式，剔除掉了估计结果中存在变量不显著的模型，最后筛选出以下五种形式的模型：ARIM A（2，2，1）-GARCH （1，1）-N、AR IM A （2，2，1）-6AR CH （3，1）-N、AR IMA（2，2，1）-6AR CH （2，1）-T、AR IMA （2，2，1）-GARCH （1，0）-GED和AR IM A （2，2，1）-G6ARCH （2，0）-GED。

对五种模型分别进行参数估计和预测，得到的结果如表7所示。根据AIC、SC、调整后的可决系数、对数似然函数值、是否可以消除ARCH效应以及平均绝对百分误差M APE这六项指标综合判定，选择ARIMA （2，2，1）-6AR（H（1，0）-GED为预测模型的最终形式，方程表达式为：

结论

本文基于2015年1月4日至2015年12月28日的上海银行间隔夜拆放利率分别构建了ARIMA模型和AR IMA-6ARCH模型，以期对上海银行间隔夜拆放利率做出短期预测。基于模型估计结果，得出以下结论：

1.2015年1月4日至2015年12月28日的上海银行间隔夜拆放利率组成的时间序列是非平稳的，取对数后的二阶差分序列为平稳序列；

2.在AR IMA模型的几种形式中，ARIMA（2，2，1）模型是最优的预测模型；

3.AR IMA （2，2，1）模型的残差序列具有显著的ARCH效应；

4.通过反复测算，分别考虑了方程的误差在正态（高斯）分布、学生t分布和广义误差分布（GED）三种不同分布下的不同形式，最后确定ARIMA （2，2，1）-6ARCH（1，0）-GED为预测模型的最终形式。ARMA （2，2，1）-GARCH（1，0）-GED模型相较于ARIMA （2，2，1）模型很好地消除了ARCH效应，并且对数似然函数增加了，AIC和SC都变小了，同时平均绝对百分误差MAPE也变小了，这说明ARIM A （2，2，1）-GAR CH（1，0）-GED模型相较于ARIMA（2，2，1）模型能够更好地对上海银行间隔夜拆放利率作出短期预测；

5.GED分布假设下AR IMA-GARCH模型的估计结果要优于正态分布假设下的估计结果。