角，原来还可以这样量

王逸卿

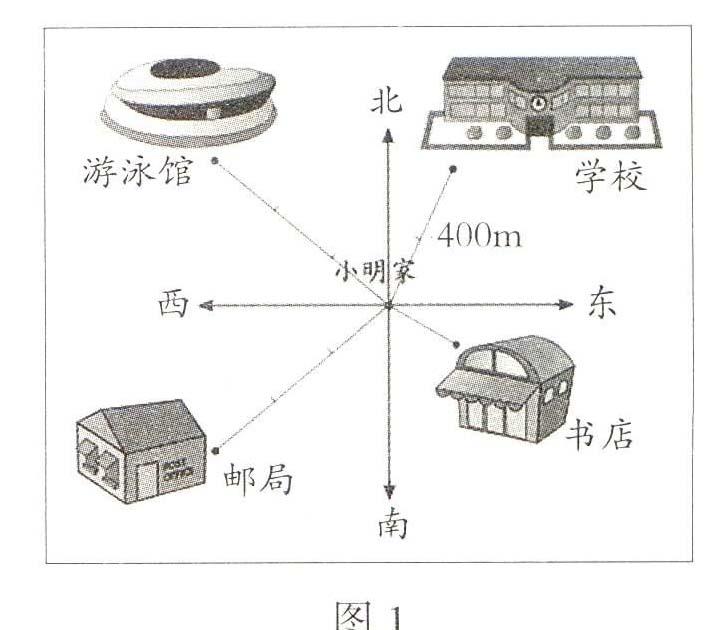
人教版小学数学六年级上册“位置与方向（二）”单元中，教材提供了这样一道习题（如图1）。习题要求以小明家为观测点，描述学校、游泳馆、邮局、书店的位置。第一个填空是：“学校在小明家北偏 方向上，距离是 米”。我让学生尝试着填一填。巡视时发现不少学生不停地转动着量角器，有的学生费了很大的劲也没有量对。

细细分析，我们可以发现，主要原因是这个角的两条边都不在水平方向上，学生量这样的角存在困难。如果此题改为：“学校在小明家东偏 方向上，距离是 米”，学生就容易量对。当然，如果仅仅从获得结果的角度看，我们确实可以指导学生量出东偏北的角度，然后用90°- 65°得到北偏东是25°。但这样就降低了量角的难度。笔者认为学生量角的能力不能停留在这样的水平上。

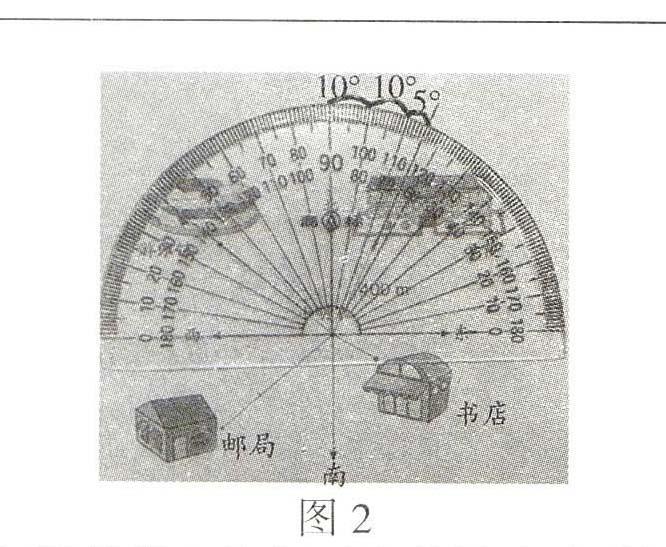
于是，在分析的时候，笔者将量角器水平放置（如图2）。从90°位置开始往右数：“请同学们看大屏幕，一个大格、两个大格、还有半个大格，10°+ 10°+ 5°= 25°。这时，不少学生露出了惊讶的表情，一位学生竟然情不自禁地喊道：“还可以这样量？”

六年级的学生为何对这种量法感到如此惊讶？这与四年级《角的度量》一课的学习又有什么关系？

“量出指定角的度数”属于操作技能，可以归为典型的程序性知识学习范畴。程序性知识的学习需要明晰相应的操作流程。与实验教科书相比，人教版的新教材提炼出了量角的步骤：“第一步，把量角器的中心与角的 重合，0°刻度线与角的一边 。第二步，角的另一边所对的量角器的刻度，就是这个角的 。”面对程序化知识的学习，掌握一般的步骤是必不可少的。学生只有明确了相应的操作步骤，再加以一定量的练习，才能正确而熟练地量出角的度数。

这样想来，四年级《角的度量》一课的学习中，我们直接从量角器量角入手，也能够让学生学会量角的方法。但如果这样，多数学生看到的量角器，仅仅是一条条线和一个个度数，而没有看到一个个角。掌握的也仅仅是测量的方法而不是测量的本质。于是，他们量角的方法很机械，以至于稍有变化，学生就不知所措，也不明白为什么“神奇”的量角器上的度数就是这个角的度数。

因此，笔者认为仅仅掌握这样的步骤是不够的，学生更需要明白这样操作的道理。有位教师在上“角的度量”一课的时候，就先抛开教材提供的“量角步骤”，从圆的等分入手，揭示了量角的本质。

教师首先给学生建立了1°角概念：即人们将圆平均分成360份，将其中一份所对的角作为度量角的单位，它的大小就是1°。然后教师呈现了一个四等分的圆（如图3），问学生：“你看到角了吗？”学生表示看到了4个直角。教师接着问：“每一个直角是几度？你是怎么知道的？”学生列出了这样的算式：360°÷ 4=90°。随后，教师又将其中的一个直角平均分成了9份，呈现了第二个圆（如图4）。教师又问道：“看见更多的角了吗？你知道这样的一个角（教师指着其中一个小的角）是多少度吗？”一位学生答道：“这个角是10°”教师继续问：“你是怎么知道的？”第二位学生答道：“90°÷ 9=10°”。之后，教师呈现了一个任务：“请你利用这个图形量出下列两个角的度数。”（教师提供了2个印在透明纸上的角。）

学生很快就完成了度量。教师呈现了一位学生的度量结果（如图5），问学生：“两个角各是几度？你是怎么知道的？”学生回答：“∠1是30°，因为1个小的角是10°，3个小的角就是30°；∠2是50°，因为1个小的角是10°，5个小的角就是50°。”教师又呈现另一位学生的作品（如图6），学生摆的位置不同，量的方法和结果相同。在这个测量过程中，学生体会到“包含几个10°角，这个角就是几十度，而角摆的位置可以不相同”。

角的度量其实就是用量角器上已知度数的角度量生活中未知角的度数。量角器就是角的集合。这位教师巧妙地设计了这样测量的环节，让学生应用10°角量出了30°的角和50°的角，明白了30°的角就是由3个10°角组成，50°的角就是由5个10°角组成。有了这样的体验，他自然也会明白量角器上的30°里面包含了30个1°角，有了这样的体验，到了六年级学生还会发出上面的惊讶声吗？

程序化知识的教学中掌握规范的操作流程十分重要，但是我们的教学又不能直奔流程而去。我们需要花更多的时间去引导学生理解流程背后的道理。只有真正明白了其中的道理，操作才能变得灵活，否则就会走向僵化。

【责任编辑：陈国庆】