巧设学生提问 优化数学教学
2016-05-14陆琪松顾建锋
陆琪松 顾建锋
【摘要】 数学教学中的一个普遍现象是师问生答,这样的教学方式看似做到了师为主导,生为主体,实则还是教师为中心,学生只是被动地接受问题的设计,其主体地位没有得到充分体现,不利于学生质疑、探究、创新能力的发展. 而学生提问就是让学生从自己需要的角度出发去准备问题,并针对自己未知的领域,通过观察、比较、分析和综合,提出一些具有代表性的问题,这是数学教学新的要求.
【关键词】 学生提问;让生提问;数学教学;新知
《义务教育数学课程标准(2011年版)》在原有分析和解决问题的基础上,新增了发现和提出问题的能力目标,这是基于培养学生创新意识和创新能力的考虑,体现了数学课程对时代对人才培养要求的主动适应,当然对于数学教学也提出了新的要求.为此,数学教师的教学理念和行为都应作出适当的调整与改变,努力创设有利于学生发现和提出问题的课堂环境,引导学生用数学的眼光看世界,鼓励学生用数学的思维方式发现和提出问题.近来,笔者尝试实践将学生提问融入数学课堂教学,小有收获.下面笔者以浙教版教材学习为例,简述学生课堂提问的几点做法,与同行交流.
一、上课伊始时让生提问,新知引出事半功倍
教育家陶行知说过:“发现千千万,起点是一问.” 从数学教学来说,当学生感到要问“是什么”、“为什么”、“怎么办”时,其主动性思维将会真正激发和启动,学习积极性也将持续保持.基于此,在上课伊始时设置学生提问情境,让学生带着问题走进数学世界,则新知学习将事半功倍.
案例1 浙教版八上《4.2平面直角坐标系》新课导入教学片断
上课伊始,教师创设如下对话情境:
师:“数学学习就是从发现问题、提出问题到分析问题、解决问题的过程.今天我们要学习的内容是《4.2平面直角坐标系》,看到这个课题你能发现并提出怎样的问题?”
生1:什么是平面直角坐标系?
生2:如何表示平面直角坐标系?
生3:平面直角坐标系有什么用?
师:布置预学任务:(1)阅读书本119页内容,尝试解决同学提出的问题.(2)你还能提出什么新的问题?
评析:古人云:“学贵知疑,小疑则小进,大疑则大进.”疑问是主动思维的火花塞,是积极学习的发动机.本案例中,学生通过观察课题提出的三个问题,切中了本课时新知学习的重点,指引了新知学习的方向(即“是什么”、“为什么”、“怎么用”),引起了全体学生的共鸣,学习氛围悄然形成.相对教师提出问题,学生自己提出的问题,更能让学生处于一种求知的“愤悱”状态,也更迫切地想对新知一探究竟.此时,后续学习的路径清晰可辨,教学活动的展开水到渠成.
二、概念阅读时让生提问,新知获得浅入深出
教材文本是经过专家们反复论证而编排的,很多概念的文字描述虽浅显易懂,但闪耀着智慧的光芒,蕴藏着深刻的内涵,隐含着丰富的外延,需要教师和学生一起仔细研读、细细品味、追根溯源.因此,概念学习时,若能在学生阅读教材文本后,设置学生课堂提问环节,表述个人对概念文本的理解和疑惑,询问概念的来龙去脉,则新知获得就能做到寻本挖源、浅入深出.
案例2 浙教版八下《5.1四边形》概念教学片断
师:请同学们打开书本,阅读书本94页第一自然段,思考四边形定义的描述,提出自己的疑问.
生1:四边形的4个顶点可否不在同平面内?
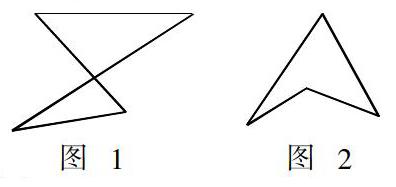
生2:这样的图形算不算四边形(如图1和图2)?
生3:四边形的外角共有几个?
生4:三角形的3条边有大小关系,四边形的4条边有大小关系吗?
生5:三角形有符号表示,四边形有符号表示吗?
评析:本案例中,教师仅仅为学生搭建了自由提问的舞台,学生却回赠给教师一个个灵动地、闪耀着智慧火花的问题.生1、生2所提问题涉及四边形定义的内涵,生3、生4、生5所提问题恰与四边形定义的外延有着诸多联系.值得一提的是,生2给出的图形1是一个“折四边形”,不管其四个顶点在不在同一平面内,均符合书本四边形的定义(由不在同一条直线上的四条线段首尾顺次相接形成的图形叫做四边形),这个图形或许会给教师带来一些尴尬,但这恰恰是学生创新思维的具体体现;生4与生5则充分运用类比学习的方法,联想三角形的有关概念与性质,提出了四边形的研究问题,说明发现问题、提出问题以及数学学习的方法已在他们心中生根发芽.
三、例题学习时让生提问,新知应用本固枝荣
书本例题具有典型性和示范性,是学生新知应用的桥梁,也是甄别学生新知掌握程度的“试金石”.因此,为更好地凸显例题的教学价值,在例题学习时营造学生提问的氛围,鼓励学生说出自己的不解和困惑,这样,他们的思维将处于积极思考状态,心智潜能也将得到有效发展,进而促使新知应用本固枝荣.
案例3 浙教版七下教材《用加减消元法解二元一次方程组》例题教学片断
……
师:请用加减消元法解方程组2s + 3t = 2
2s - 6t = -1.
师:先请同学们独立尝试解答,若没有思路,可以参阅书本43页例3的解题过程.
生:动笔解答.
师:现在请同学们说说你在解此方程组时碰到的困难和思维受阻点.
生1:老师,虽然通过看书我明白了用加减消元法解这个方程组的方法,但对于用加减消元法解方程组,我还是不太清楚什么时候用“加法消元”?什么时候用“减法消元”?
师(转向其他学生):生1同学提的问题,也是我心中的困惑,谁能帮我们解开困惑?
生2:用加减消元法解方程组的关键是观察所给方程组里相同字母系数的特征,当相同字母的系数相等时用“减法消元”,当相同字母的系数是相反数时用“加法消元”.
师:哦,原来如此,我明白了,生1同学你呢?
生1:哦,明白了,可是:“如果在方程组中既没有相同字母的系数相等,也没有相同字母的系数是相反数,那么又该如何处理呢?”
师:了不起!生1同学的问题具有前瞻性,的确在我们用加减消元法解方程组时,会碰到相同字母的系数既不相等,也不是互为相反数,对此,其他同学有好的解决方法吗?
生:……
评析:上述案例中,教师为解题思路受阻的学生营造了提问的氛围,制造了学生质疑和学生释疑的机会,使得例题教学焕发了新的生机.生1同学针对自己未知的领域,通过观察、比较和思考提出的两个问题,恰好命中加减消元法解方程组的关键,同时也引发了其他学生的思考.这样,伴随着问题的提出与解决,在生问生答之间,数学知识与方法的奥秘被抽丝剥茧,层层剥开,学生也在此过程中体会到了学习的方法与乐趣.
四、当堂训练时让生提问,新知拓展入木三分
数学教学离不开当堂训练,它是对本课时所学新知的巩固与拓展,也是提升学生解题能力的需要.当堂训练时,数学教师擅长将习题进行变式重组,此时若能融入学生提问的场景,搭建学生改题、变题和出题的平台,则可达到以一当十的练习效果,有利于激发学生学习的潜能,培养学生发散性思维能力和创造性思维能力,使得新知拓展入木三分.
案例4 浙教版七下教材《乘法公式1》当堂训练教学片断
……
评析:教师通过示范引领,暗示了习题变式的一般方法,紧接着为学生搭建变题、出题的平台,让学生提出问题与变式训练实现无缝对接.纵观4道变式题,每道题与原题之间不仅有着明显的差异,而且4道题自上而下呈由易到难、由熟到疏、层层递进的状态排列,其中,生1、生2的问题能起到巩固新知的作用,生3、生4的问题既是对新知的拓展应用,又为学生下节课学习完全平方公式埋下伏笔,可谓一举两得.此外,从未成年人心理特点上来说,由于出题的人是学生,更能激起其他学生的好胜心,相信随着4个问题的解决,学生们必定会经历一场思维风暴,其知识和能力也必将得到一定程度的提升.
五、结 语
总而言之,课堂是数学教学的主阵地,也是发展学生能力的加油站.在不同的课堂教学阶段设置学生提问环节,让每一名学生根据自己的需要对所学知识存在的疑惑或新见解提出问题,这尊重了学生学习的主体地位,调动了学生的主观能动性,落实了“四能”目标,优化了数学教学,符合“学为中心”的教学改革方向.其中理解学生、理解教材和理解教学是对数学教师的前提要求;对学生提问情境的创设、提问氛围的营造、提问场景的搭建以及提问时机的把握是数学教师的关键能力要求;引领学生提问并根据学生提问的实际情况给予正确评价是数学教师要掌握的核心技巧.日常的数学教学若能长此以往,学生课堂提问会渐渐地成为习惯,创新能力的发展会慢慢地成为现实,对数学学习的炽爱也会逐渐地成为一种常态.
【参考文献】
[1]中华人民共和国教育部制定.义务教育数学课程标准(2011年版)[M].北京:北京师范大学出版社,2012.
[2]王丽娟.初中数学“预学—展评”课堂教学转型的实践.浙江教学研究,2014(1):30-32.
