带交叉算子的量子粒子群优化算法
2016-05-09陈汉武朱建锋刘志昊赵生妹
陈汉武 朱建锋 阮 越,2 刘志昊 赵生妹
(1东南大学计算机科学与工程学院,南京 210096)(2安徽工业大学计算机科学与技术学院,马鞍山 243005) (3南京邮电大学通信与信息工程学院,南京 210003)
带交叉算子的量子粒子群优化算法
陈汉武1朱建锋1阮越1,2刘志昊1赵生妹3
(1东南大学计算机科学与工程学院,南京210096)
(2安徽工业大学计算机科学与技术学院,马鞍山243005) (3南京邮电大学通信与信息工程学院,南京210003)
摘要:为了改善量子粒子群优化(QPSO)算法、提高其求解多峰优化问题的能力,采用新的粒子吸引点和势阱特征长度计算方法,引入遗传算法中的交叉算子并融入交叉概率自适应的参数控制技术,设计了一种带交叉算子的量子粒子群优化(CQPSO)算法.CQPSO算法既可确保QPSO粒子群体的多样性、维护粒子整体的活力性,又能克服特殊情况下QPSO算法收敛的不稳定性和陷入局部最优的偶发性.实验结果表明,在21个标准测试函数中,无论对应单峰函数、多峰函数或是偏移、旋转函数,在相同的物理仿真平台上,CQPSO算法的性能在绝大多数情况下都优于其他改进的量子粒子群算法,从而验证了CQPSO算法的有效性和鲁棒性.
关键词:量子粒子群优化;交叉算子;局部优化;多峰函数;收敛
引用本文:陈汉武,朱建锋,阮越,等.带交叉算子的量子粒子群优化算法[J].东南大学学报(自然科学版),2016,46(1) : 23-29.DOI: 10.3969/j.issn.1001-0505.2016.01.005.
粒子群优化(PSO)算法是一种重要的群体智能随机搜索算法[1-2],因其概念简单、易于实现而备受关注[3-5].但PSO算法存在易早熟的问题,不能完全保证全局收敛[6].文献[7]针对研究多维空间中粒子群运动轨迹时PSO算法的稳定性和收敛性进行了讨论.受量子力学研究对象具有随机行为特征的启示,Sun等[8-9]提出了一种基于量子力学的量子粒子群优化(QPSO)算法,并证明了该算法的全局收敛性[10]优于PSO算法.在QPSO算法中,基于量子计算的内禀性,每一个粒子都可以通过学习种群全体的历史最优位置(gBest)来修正自己的搜索方向,故算法具有快速收敛的特征.但对于求解复杂多极值问题时,受极值的物理分布以及初始种群选择等因素的影响,特定情况下搜索过程中若出现的种群全体历史最优位置是一个不实的gBest,则该算法同样也会导致群体多样性降低,引发整个群体易于陷入局部最优,最终导致算法早熟收敛.
为了改善QPSO算法的整体性能,研究者们提出了多种改良方法.文献[11]提出了2种参数调节方法,使收缩-扩张系数随迭代次数增加而线性减小或依据个体的适应值动态调整收缩-扩张系数;文献[10,12]分别采用随机选取的个体历史最优位置和加权平均最优位置替代QPSO算法中的平均最优位置;文献[13]提出了一种随机选择学习粒子的方法,如果随机选取的粒子的适应值优于当前个体,则将该粒子作为学习粒子,否则仍然以群体中适应值最好的粒子作为学习粒子;文献[14]使用高斯分布生成个体吸引点;文献[15-17]采用多种群协同进化的方法,利用多个协作的粒子群分别优化解向量的不同部分,从而增强算法的搜索多样性;文献[18]提出了一种多粒子协作的方法,将多个经过多次测量得到的粒子进行协作,以便更好地获取每个粒子中包含的有用信息.此外,学者们还将OPSO算法与模拟退火算法[19]、免疫算法[20-21]、差分演化[22]、单纯形法[23]等其他方法进行融合或结合变异算子[24-25]、局部搜索算子[26]、混沌搜索[27]、公共历史搜索[28]等技术,以达到改进算法的目的.
本文将遗传算法中的交叉算子引入QPSO算法中,提出了一种带交叉算子的量子粒子群优化(CQPSO)算法.
1 量子粒子群优化算法
在PSO算法中,群体内每个个体被称为一个粒子,表示待求解问题的一个潜在解.粒子i(i =1,2,…,N)可由2个向量表示,即速度向量Vi,t=和位置向量,其中D为待求解问题的维数,t为当前的迭代次数.在每一次迭代中,令为粒子i到目前位置搜索到的最优位置,Pg,t=为整个群体迄今为止搜索到的最优位置,可根据下式更新粒子i的速度与位置:
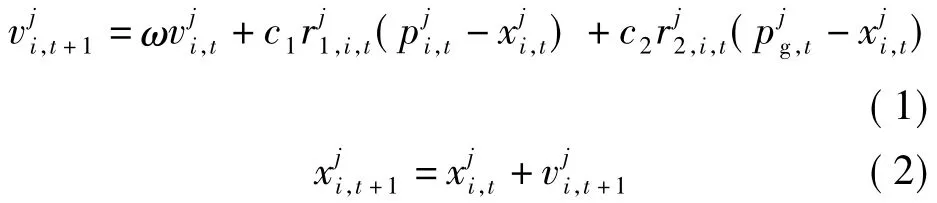
式中,ω为惯性权重[29]; c1,c2为加速系数;为[0,1]之间满足均匀分布的随机数.
文献[7]表明,群体中粒子i在演化过程中会以自身历史最优位置Pi,t和群体历史最优位置Pg,t的加权平均位置为吸引点,并逐渐趋向于该点.Si,t的计算公式如下:
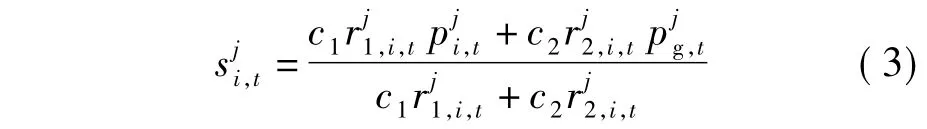
PSO算法中,一般取c1= c2,故式(3)可改写为

基于以上对PSO算法中粒子运动轨迹的分析,QPSO算法假定粒子群系统是一个满足量子力学基本假设的粒子系统,粒子i在第j维上是在以点为中心的δ势阱中运动,具有量子基本行为特征,则其状态可由波函数Ψ描述,即
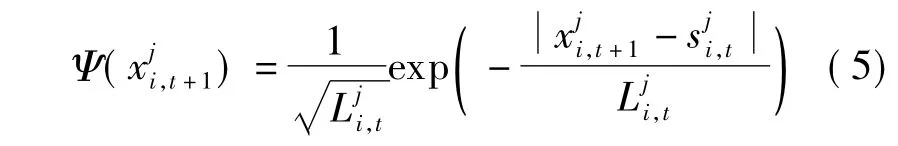
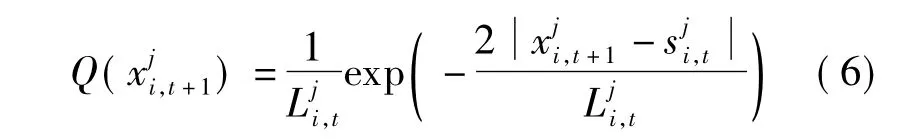
为了得到粒子的位置,需要将粒子的状态由量子态塌缩到经典态,采用Monte Carlo随机模拟的方法来测量粒子的位置,从而得到粒子的位置更新方程为
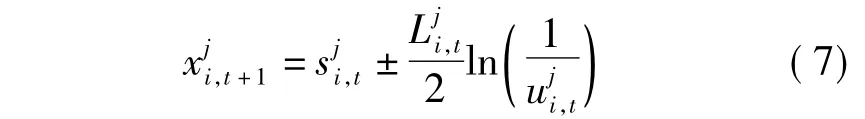
粒子i在第j维的概率密度函数为
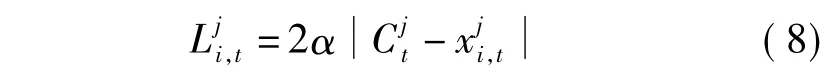
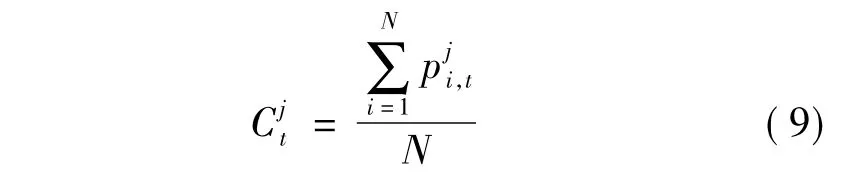
2 带交叉算子的量子粒子群算法
2. 1粒子吸引点
在QPSO算法中,每个粒子将个体历史最优位置Pi,t与群体历史最优位置Pg,t的加权平均位置Si,t作为自身的吸引点.这种计算方法以粒子运动轨迹的分析结果[7]为指导,具有计算简单的优点,但也存在2个明显的问题:①每个粒子除了学习自身的经验外,只以群体的历史最优位置为引导,导致大群体的多样性下降速度过快,降低了算法求解复杂多峰优化问题的性能;②根据式(4)得到的吸引点将限定在以个体历史最优位置Pi,t和群体历史最优位置Pg,t为对顶点的D维超矩形内,随着算法演化过程的进行,每个粒子吸引点的可能分布空间逐渐减小,使粒子吸引点逐渐趋向于群体历史最优位置,最终导致算法在后期跳出局部最优的能力不足.
为了避免吸引点只能限定在特定区域的问题,可将吸引点的计算公式改写为

式中,βi,t为区间[0,1]上均匀分布的随机数;下标a 为随机选取且适应值最好的个粒子中的一个粒子,选取粒子的比率q∈(0,1];为扰动向量,且
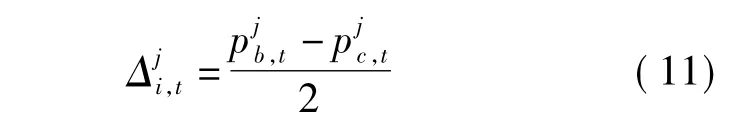
式中,下标b,c为群体中随机选取的2个粒子,且a≠b≠c≠i.
利用这种关于粒子吸引点的计算方法,可以提高算法求解多峰优化问题的性能.这是因为当某个粒子陷入局部最优时,分布在其他搜索空间中的粒子有机会帮助该停滞粒子逃离局部最优.
为了克服上述缺点,参考2. 1节中的粒子吸引点计算方法,参数可按照下式进行计算:

根据式(12),即使在多数粒子都陷入局部最优时,由于依然存在部分分散在其他区域中的粒子,使得每个粒子仍然具有适度的概率逃离局部最优,从而提高了算法的全局搜索能力.
2. 3交叉算子
交叉算子源于遗传算法[30].通过交叉操作可以进行群体中个体的信息交换,并随着演化过程的延续逐渐保留那些优秀的基因,使群体能够往好的方向进化.为了增加群体的多样性,提高算法求解复杂多峰优化问题的性能,本文将交叉算子引入到QPSO算法中.
首先,根据式(7)、(10)、(11)与(12),生成粒子i对应的测量位置Xi,t +1;然后,将测量位置Xi,t +1与个体历史最优位置Pi,t进行离散交叉,生成测试位置.交叉公式为

式中,randj(0,1)为[0,1]之间满足均匀分布的随机数; jrand为[1,D]上随机均匀产生的整数; p为交叉概率.这种交叉方式与差分演化[31-32]中的二项交叉操作相同.
最后,按照下式更新粒子的个体历史最优位置:
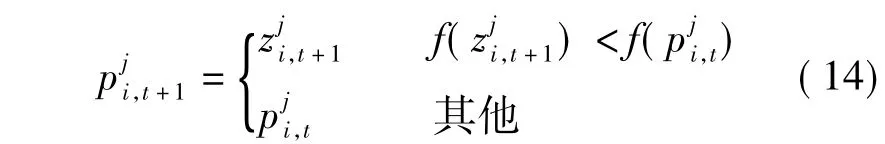
式中,f(·)为适应值函数.不失一般性,本文仅考虑最小优化问题.
交叉概率p的取值对算法的搜索能力和收敛速度具有重要影响.较小的交叉概率可以使群体中个体更多地保留自身的信息,维持较高的群体多样性,有利于算法进行全局探索;相反,较大的交叉概率促使个体更多地学习群体中经验知识,从而加快算法的收敛速度.
2. 4参数控制
不同优化问题以及同一优化问题在进化的不同阶段需要设置不同的最优参数.因此,难以选定适合所有问题的p值.参照文献[31]中的参数自适应方法,本文将参数p直接编码到每个粒子中,以实现自适应控制.扩展编码后群体中粒子i可描述为
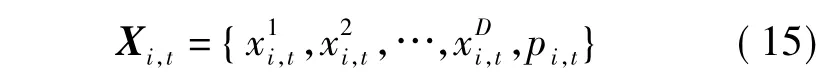
对于群体中的每个粒子,采用如下规则更新交叉概率:

式中,τ为参数pc的更新概率.
参照文献[32],本文提出了一种改进的交叉概率修复方法.为便于描述,将粒子i关联一个额外的二进制向量
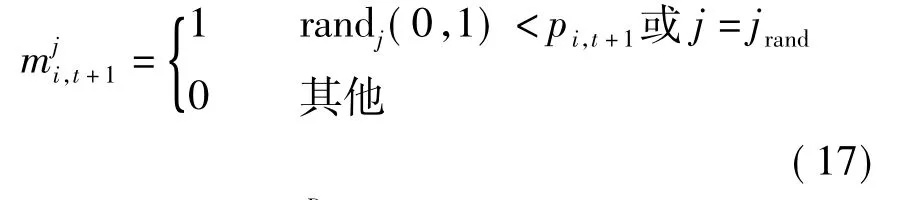
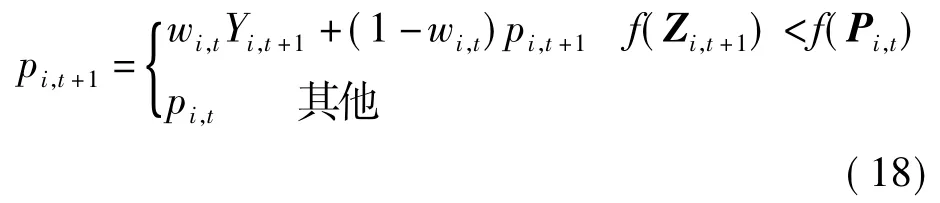
式中,wi,t为[0. 9,1]之间满足均匀分布的随机数.
收缩-扩展系数α采用的更新方法为:随着迭代次数的增加,α线性减小,即
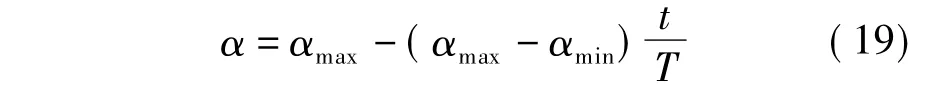
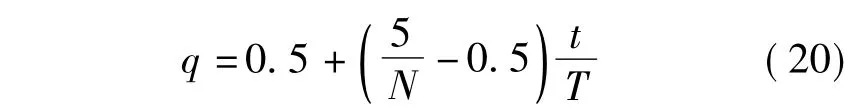
2. 5 CQPSO算法
结合以上给出的粒子位置更新方法和参数控制方法,设计了一种带交叉算子的量子粒子群算法.该算法中,每个粒子的吸引点都不会局限在特定的搜索空间中,从而增强了每个粒子的探索能力.同时,该算法采用了参数自适应的控制方法,使
式中,T为设定的最大迭代次数.
选取粒子的比率q取值较大时,算法的全局探索能力较强;相反,q取值较小时,则有利于算法快速收敛.为了平衡算法在搜索前期的全局搜索能力与后期的局部搜索能力,q的取值随迭代次数的增加而线性减小,即得每个粒子通过学习先前的经验逐步自适应调整参数的取值.CQPSO算法的伪代码描述如下:

3 实验结果与比较
为了验证CQPSO算法的有效性,选取了21个标准测试函数用于实验测试(见表1).表中的测试函数可以分为3类:①单峰函数f1~f7;②多峰函数f8~f13;③偏移、旋转函数f14~f21.在21个维数D = 30的标准测试函数上,比较了QPSO[9],MQPSO[13],QPSO-RM[10],WQPSO[12],CQPSO等5种算法.
实验中CQPSO算法的参数设置如下:群体规模N = 50;收缩-扩展系数α从0. 7线性减小到0. 1;每个粒子的初始交叉概率均为0. 9;交叉概率的更新概率τ=0. 2.
为了进行公平比较,QPSO,MQPSO,QPSORM,WQPSO算法的群体规模也都设置为50,其他参数则按照原文献设置,即QPSO算法与WQPSO算法的收缩-扩展系数从1线性减小到0. 5,MQPSO算法的收缩-扩展系数从1线性减小到0. 4,QPSO-RM算法的收缩-扩展系数从0. 6线性减小到0. 5.此外,在每个测试函数上,每种算法都进行2×105次函数评价(FEs).为了减小统计误差,5种算法在每个测试函数上独立运行50次,取50次运行的平均结果进行分析与比较.实验的测试环境设置如下:操作系统为Windows 7,处理器为AMD PhenomTM8450 Triple-Core,内存为2 GB,编程语言为C + +,编译器为VS C + +2008.

表1 21个标准测试函数
表2给出了所有算法在各个测试函数上50次运行的平均结果和标准方差.由表可知,CQPSO算法在单峰函数f1,f2,f3,f5上获得了最高精度的解; QPSO-RM算法在大多数单峰函数上具有较好的性能,并且在函数f4上获得了最好的解;虽然MQPSO算法在单峰函数上的收敛速度较慢,但其在噪声函数f7上获得了最好的解.
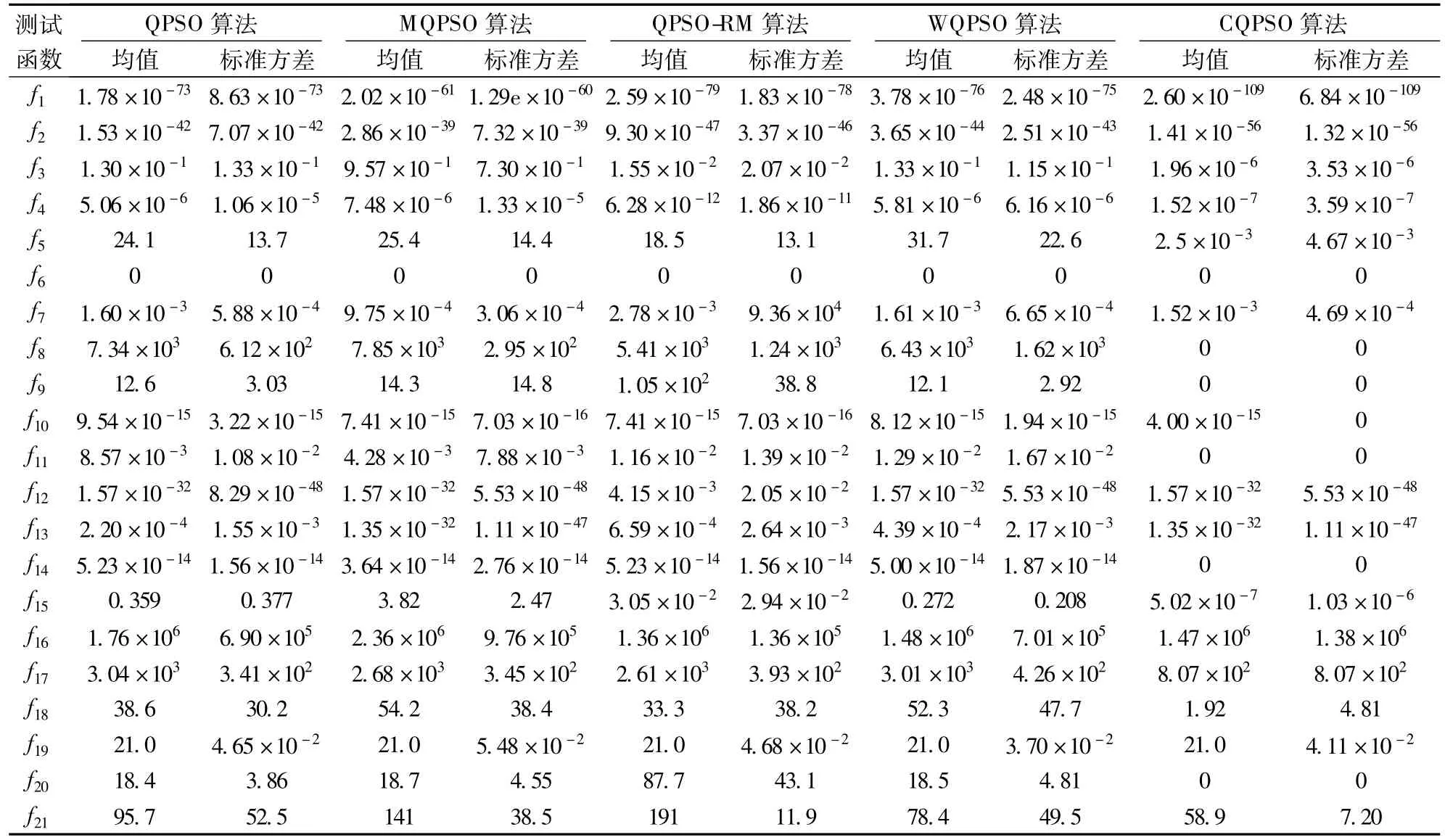
表2 5种独立运行50次的均值与标准方差
其次,CQPSO算法在复杂多峰函数f8~f13上也获得了最好的结果.尤其是对于函数f8,f9和f11,其他4种算法都陷入了局部最优,仅CQPSO算法获得了最好的解.由此表明,CQPSO算法能够维持较好的群体多样性,增强了算法跳出局部最优的能力,在复杂多峰函数上具有较高的搜索精度.在CQPSO算法中,每个粒子都向群体中适应值最好的粒子学习经验,故算法仍然具有较快的收敛速度.
函数f14~f17为单峰函数,函数f18~f21为多峰函数.经过偏移、旋转变换后,这些函数变得难以求解.从实验结果可以看出,CQPSO算法在测试函数f14,f15,f17,f18,f20,f21上获得的解的质量优于其他4种算法.
综上所述,CQPSO算法在大多数标准测试函数上的性能要优于其他4种算法.CQPSO算法在保持快速收敛的同时,较传统QPSO算法以及其他几种改进的QPSO算法具有更好的全局搜索能力.
4 结语
本文提出了新的吸引点和势阱特征长度评价方法,并在此基础上设计了一种带交叉算子的量子粒子群优化算法.通过在量子粒子群优化算法中引入交叉算子,使得群体中个体的优秀特征得以保留,提高了群体的多样性,增强了算法的全局搜索能力.同时,新的吸引点和势阱特征长度计算方法增强了算法跳出局部最优的能力.21个标准测试函数上的实验结果证明了所提算法的有效性和优良性.下一步的研究方向是如何更好地自适应调节算法参数以及改进算法的迭代策略以提高算法性能.
参考文献(References)
[1]Kennedy J,Eberhart R C.Particle swarm optimization [C]/ /Proceedings of the IEEE International Conference on Neural Networks.Perth,WA,USA,1995: 1942-1948.
[2]Eberhart R C,Kennedy J.A new optimizer using particle swarm theory[C]/ /Proceedings of the Sixth International Symposium on Micro Machine and Human Science.Nagoya,Japan,1995: 39-43.
[3]Eberhart R C,Shi Y H.Particle swarm optimization: Developments,applications and resources[C]/ /Proceedings of the 2001 Congress on Evolutionary Computation.Seoul,Korea,2001: 81-86.
[4]Hu X H,Shi Y H,Eberhart R C.Recent advances in particle swarm[C]/ /Proceedings of the Congress on Evolutionary Computation.Portland,Oregon,USA,2004: 90-97.
[5]Li X D,Engelbrecht A P.Particle swarm optimization: An introduction and its recent developments[C]/ /Proceedings of the 9th Annual Conference Companion on Genetic and Evolutionary Computation.London,UK,2007: 3391-3414.
[6]van den Bergh F.An analysis of particle swarm optimizers[D].Hatfield,South Africa: University of Pretoria,2002.
[7]Clerc M,Kennedy J.The particle swarm-explosion,stability,and convergence in a multidimensional complex space[J].IEEE Transactions on Evolutionary Computation,2002,6(1) : 58-73.DOI: 10. 1109/ 4235. 985692
[8]Sun J,Feng B,Xu W B.Particle swarm optimization with particles having quantum behavior[C]/ /Proceedings of the Congress on Evolutionary Computation.Portland,Oregon,USA,2004: 325-331.
[9]Sun J,Xu W B,Feng B.A global search strategy of quantum-behaved particle swarm optimization[C]/ / Proceedings of the IEEE Conference on Cybernetics and Intelligent Systems.Singapore,2004: 111-116.
[10]Sun J,Wu X J,Palade V,et al.Convergence analysis and improvements of quantum-behaved particle swarm optimization[J].Information Sciences,2012,193: 81 -103.DOI: 10. 1016/j.ins.2012. 01. 005.
[11]Sun J,Xu W B,Liu J.Parameter selection of quantum-behaved particle swarm optimization[J].Computer Engineering&Applications,2007,43(23) : 543-552.
[12]Xi M L,Sun J,Xu W B.An improved quantum-behaved particle swarm optimization algorithm with weighted mean best position[J].Applied Mathematics and Computation,2008,205 (2) : 751-759.DOI: 10. 1016/j.amc.2008. 05. 135.
[13]Sun J,Lai C H,Xu W B,et al.A novel and more efficient search strategy of quantum-behaved particle swarm optimization[C]/ /Proceedings of the 8th International Conference on Adaptive and Natural Computing Algorithms.Warsaw,Poland,2007: 394-403.
[14]Sun J,Fang W,Palade V,et al.Quantum-behaved particle swarm optimization with Gaussian distributed local attractor point[J].Applied Mathematics and Computation,2011,218 (7) : 3763-3775.DOI: 10. 1016/j.amc.2011. 09. 021.
[15]Gao H,Xu W B,Gao T.A cooperative approach to quantum-behaved particle swarm optimization[C]/ / Proceedings of the IEEE International Symposium on Intelligent Signal Processing.Alcala de Henares,Spain,2007: 1-6.
[16]Lu S F,Sun C F.Coevolutionary quantum-behaved particle swarm optimization with hybrid cooperative search[C]/ /Proceedings of the Pacific-Asia Workshop on Computational Intelligence and Industrial Application.Wuhan,China,2008: 109-113.
[17]Lu S F,Sun C F.Quantum-behaved particle swarm optimization with cooperative-competitive coevolutionary[C]/ /Proceedings of the International Symposiumon Knowledge Acquisition and Modeling.Wuhan,China,2008: 593-597.
[18]Li Y Y,Xiang R R,Jiao L C,et al.An improved cooperative quantum-behaved particle swarm optimization [J].Soft Computing,2012,16(6) : 1061-1069.DOI: 10. 1007/s00500-012-0803-y.
[19]Liu J,Sun J,Xu W B.Improving quantum-behaved particle swarm optimization by simulated annealing [C]/ /Proceedings of the International Conference on Intelligent Computing.Kunming,China,2006: 130-136.
[20]Liu J,Sun J,Xu W B,et al.Quantum-behaved particle swarm optimization based on immune memory and vaccination[C]/ /Proceedings of the IEEE International Conference on Granular Computing.Atlanta,GA,USA,2006: 453-456.
[21]Liu J,Sun J,Xu W B.Quantum-behaved particle swarm optimization with immune operator[C]/ /Proceedings of the 16th International Symposium on Foundations of Intelligent Systems.Bari,Italy,2006: 77-83.
[22]Jamalipour M,Sayareh R,Gharib M,et al.Quantum behaved particle swarm optimization with differential mutation operator applied to WWER-1000 in-core fuel management optimization[J].Annals of Nuclear Energy,2013,54: 134-140.
[23]Davoodi E,Tarafdar M T,Zadeh S G.A hybrid improved quantum-behaved particle swarm optimizationsimplex method (IQPSOS) to solve power system load flow problems[J].Applied Soft Computing,2014,21: 171-179.DOI: 10. 1016/j.asoc.2014. 03. 004.
[24]Liu J,Sun J,Xu W B.Quantum-behaved particle swarm optimization with adaptive mutation operator [C]/ /Proceedings of the Second International Conference on Advances in Natural Computation.Xi'an,China,2006: 959-967.
[25]dos Santos Coelho L.A quantum particle swarm optimizer with chaotic mutation operator[J].Chaos,Solitons&Fractals,2008,37(5) : 1409-1418.DOI: 10. 1016/j.chaos.2006. 10. 028.
[26]Wang J H,Zhou Y L.Quantum-behaved particle swarm optimization with generalized local search operator for global optimization[C]/ /Proceedings of the Third International Conference on Intelligent Computing.Qingdao,China,2007: 851-860.
[27]Yang K Q,Nomura H.Quantum-behaved particle swarm optimization with chaotic search[J].IEICETransactions on Information and Systems,2008,E91-D (7) : 1963-1970.
[28]Huang Z,Wang Y J,Yang C J,et al.A new improved quantum-behaved particle swarm optimization model[C]/ /Proceedings of the 4th IEEE Conference on Industrial Electronics and Applications.Xi'an,China,2009: 1560-1564.
[29]Shi Y H,Eberhart R.A modified particle swarm optimizer[C]/ /Proceedings of the IEEE World Congress on Computational Intelligence.Anchorage,AK,USA,1998: 69-73.
[30]Holland J H.Adaptation in natural and artificial systems[M].Cambridge,MA,USA: MIT Press,1992: 5-10.
[31]Brest J,Greiner S,Boskovic B,et al.Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems[J].IEEE Transactions on Evolutionary Computation,2006,10 (6) : 646-657.DOI: 10. 1109/TEVC.2006. 872133.
[32]Gong W Y,Cai Z H,Wang Y.Repairing the crossover rate in adaptive differential evolution[J].Applied Soft Computing,2014,15: 149-168.DOI: 10. 1016/ j.asoc.2013. 11. 005.
[33]Yao X,Liu Y,Lin G M.Evolutionary programming made faster[J].IEEE Transactions on Evolutionary Computation,1999,3(2) : 82-102.
[34]Suganthan P N,Hansen N,Liang J J,et al.Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization[EB/ OL].[2015-04-20].http: / /www.cil.pku.edu.cn/ resources/pso-paper/src/Optimization-Tech-Report-May-30-05.pdf.
Quantum particle swarm optimization algorithm with crossover operator
Chen Hanwu1Zhu Jianfeng1Ruan Yue1,2Liu Zhihao1Zhao Shengmei3
(1School of Computer Science and Engineering,Southeast University,Nanjing 210096,China)
(2School of Computer Science and Technology,Anhui University of Technology,Maanshan 243005,China)
(3College of Telecommunications and Information Engineering,Nanjing University of Posts and Telecommunications,Nanjing 210003,China)
Abstract:In order to improve the performance of the quantum particle swarm optimization (QPSO) algorithm and its ability to solve multimodal optimization problems,by using a new calculation method for the point of interest and the characteristic length of the potential well,an improved QPSO algorithm with crossover operator,named as CQPSO algorithm,is proposed by introducing the crossover operator in the genetic algorithm and incorporating the adaptive parameter control technology of crossover probability.The CQPSO algorithm can not only ensure the diversity of the particle group and the vigor of the particles,but also overcome the instability of convergence and accidental fall into local optimum in some special scenarios.The experimental results show that in 21 standard test functions,on the same physical simulation platform,as for whether unimodal functions,multimodal functions,offset or rotating functions,the CQPSO algorithm is superior to other improved QPSO algorithms in performance in most cases,and its effectiveness and robustness are proved.
Key words:quantum particle swarm optimization; crossover operator; local optimization; multimodal function;convergence
基金项目:国家自然科学基金资助项目(61170321,61502101)、高等学校博士学科点专项科研基金资助项目(20110092110024)、江苏省自然科学基金资助项目(BK20140651).
收稿日期:2015-06-11.
作者简介:陈汉武(1955—),男,博士,教授,博士生导师,hw_chen@ seu.edu.cn.
DOI:10.3969/j.issn.1001-0505.2016.01.005
中图分类号:TP387
文献标志码:A
文章编号:1001-0505(2016) 01-0023-07
