低复杂度大规模MIMO系统上行功率分配算法
2016-05-09范利金石
范 利 金 石
(东南大学国家移动通信重点实验室,南京 210096)
低复杂度大规模MIMO系统上行功率分配算法
范利金石
(东南大学国家移动通信重点实验室,南京210096)
摘要:为了降低莱斯信道衰落下多小区大规模多输入多输出系统上行链路功率分配算法的复杂度,提出了基于小区近似和速率的低复杂度功率分配算法.首先,给出基站采用最大比合并接收时的小区和速率近似表达式及其上下界;然后,在小区发射总功率受限及保证用户服务质量需求的条件下,提出分别基于上、下界的2种功率分配算法.这2种算法仅利用大尺度衰落等长时信道信息,减少了信道估计开销及运行功率分配算法的次数,从而降低了系统实现复杂度.仿真结果表明,与等功率分配算法相比,所提算法在低信噪比下能够显著提升系统和速率;然而,信噪比越大,性能增益越小.因此,这种新的功率分配算法可以有效应用于低信噪比情况.
关键词:大规模多输入多输出;多小区;莱斯衰落;最大比合并;功率分配
引用本文:范利,金石.低复杂度大规模MIMO系统上行功率分配算法[J].东南大学学报(自然科学版),2016,46(1) : 7-12.DOI: 10.3969/j.issn.1001-0505.2016.01.002.
MIMO技术在不增加频谱资源和天线发射功率的情况下,可以成倍地提高系统信道容量[1-2],被视为充分利用空间无线资源、提高频谱效率的核心技术,在学术界和工业界引起了广泛关注.为了满足日益增长的无线数据传输需求,Marzetta[3]于2010年提出了massive MIMO技术,在基站端部署较现有系统中天线数目高若干数量级的天线阵列,从而为数量相对较小的用户提供服务.massive MIMO技术可以通过低复杂度的线性收发处理,成倍地提升系统容量与能量效率[4-6],已经成为第五代移动通信的关键技术之一[7].
随着massive MIMO理论研究的深入,考虑的信道模型从最初的瑞利信道[3-4]扩展到有限维信道模型[8]以及存在直射径(LoS)的莱斯信道[9].然而,在文献[4,9]中,用户分配了相同的发射功率,无法充分利用无线信道的衰落来提升传输速率.为此,文献[10]提出了一种迭代算法,用于联合优化用户发送功率和上行接收矩阵,复杂度较高.为了降低功率分配实现复杂度,本文研究了莱斯信道衰落下,基站采用MRC接收机的多小区massive MIMO系统中的低复杂度功率分配算法.首先给出系统模型;然后,对基站采用MRC接收机的可达和速率进行分析,并提出了2种低复杂度的功率分配算法;最后,通过数值仿真对算法进行验证.
1 系统模型
考虑多小区上行传输场景,中心小区周围环绕L个干扰小区.其中,各个小区基站配置由M根天线组成的均匀线性阵列,在同一时频资源上服务N个单天线用户.中心小区基站接收信号为

式中,Λl= diag(p1l,…,pnl,…,pNl),pnl为小区l(l =0,1,…,L)中基站允许用户n进行发射的功率; xl∈CN×1为小区l中所有用户的发射信号矢量; n0∈CM×1为服从零均值单位方差的加性高斯白噪声; G0l为信道矩阵,且
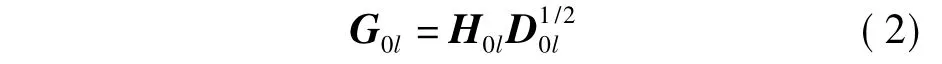
式中,D0l= diag(β01l,…,β0nl,…,β0Nl),β0nl为小区l中用户n到中心小区(l = 0)基站的大尺度衰落系数; H0l为小区l中所有用户到中心小区基站的快衰落信道矩阵.本文采用文献[9]中提出的含有LoS径的信道模型,则

式中,Ω0l= diag(K01l,…,K0nl,…,K0Nl),K0nl为小区l中用户n到中心小区基站的信道莱斯因子;^H0l∈CM×N为服从零均值、单位方差的复高斯分布的快衰落信道矩阵;珚H0l为确定矩阵,其元素为
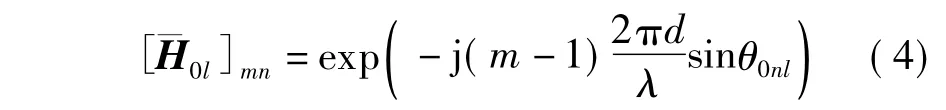
式中,d为天线间距;λ为载波波长;θ0nl为小区l中用户n到中心小区基站的LoS径到达角.为方便分析,本文取d =λ/2.
假设各个小区能够精确获取本小区用户瞬时信道状态信息和干扰小区长时信道状态信息,包括LoS径到达角θ0nl与发射功率矩阵Λl、干扰用户到达本小区的大尺度衰落β0nl、莱斯因子K0nl等.基站采用线性接收机,接收矩阵Al∈CM×N,中心小区经过接收机处理的信号为
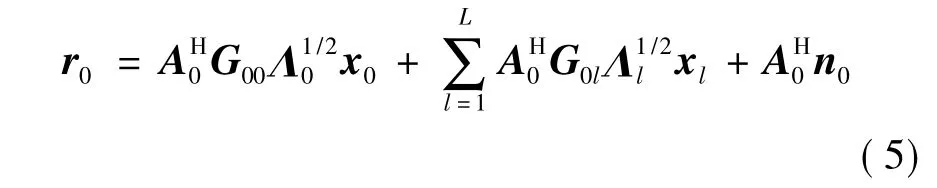
r0中的第n个元素为
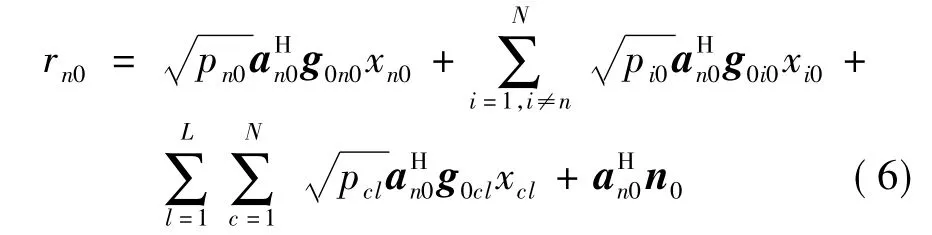
式中,an0为矩阵A0的第n列; g0cl为G0l的第c列,表示小区l中用户c到中心小区基站的信道矢量; xcl为小区l中用户c的发送信号.
与文献[4]类似,针对一次固定的信道实现,将干扰和噪声建模为独立于xn0的高斯随机噪声,其均值为零,方差为,从而获得可达速率的一个下界,即中心小区用户n的可达速率为

式中,E{·}为期望函数.
2 和速率分析
本节针对基站采用MRC接收机的情况,对式) (7)进行分析,探索和速率与天线数目、信道LoS径等因素之间的关系,为功率分配算法的设计提供依据.基站采用MRC接收机时,A0= G00,即an0= g0n0,则式(7)可表示为
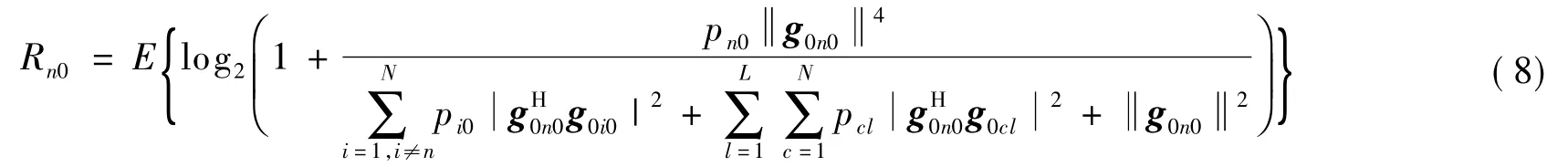
由文献[9]可知,


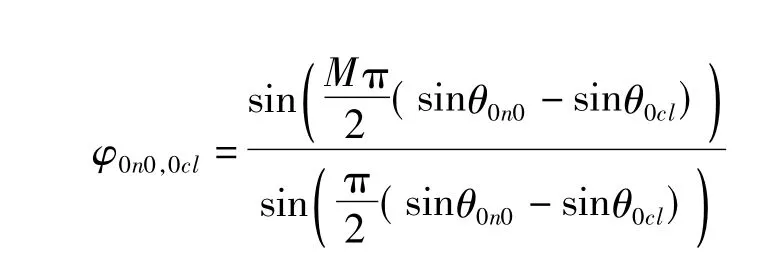
根据文献[9]中引理1,式(8)可近似为

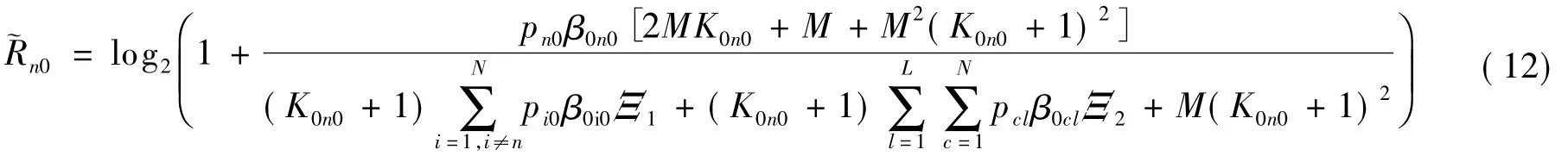
式中

1)对于没有直射径分量的瑞利信道(即K0nl=0),式(12)退化为

显然,用户可达速率与小区内以及小区间用户相关,这是MRC接收机不能消除用户间干扰带来的必然结果.若各用户采用相同发射功率(即pnl= P/M,P为一个常量),则当M趋于无穷时,有

这与文献[4]中给出的单小区结果一致,表明在基站拥有准确信道状态信息时,massive MIMO系统中发射功率为P/M的用户可达速率与不受用户间干扰和快衰落影响且发射功率为P的单输入单输出系统可达速率一致.值得注意的是,式(14)根据式(13)推导而来,描述的是多小区场景,但结果却与文献[4]给出的单小区结果一致;这其实并不矛盾,因为随着天线数目的增长,用户间干扰和快衰落噪声带来的影响逐渐消失,用户可达速率仅与大尺度衰落有关[3].
2)在毫米波大规模MIMO系统中,信道由为数不多的几条可分辨径构成.考虑信道仅包括1条LoS径的情况,且满足K0nl= K,n =1,2,…,N,l = 0,1,…,L.当K→∞时,式(12)退化为
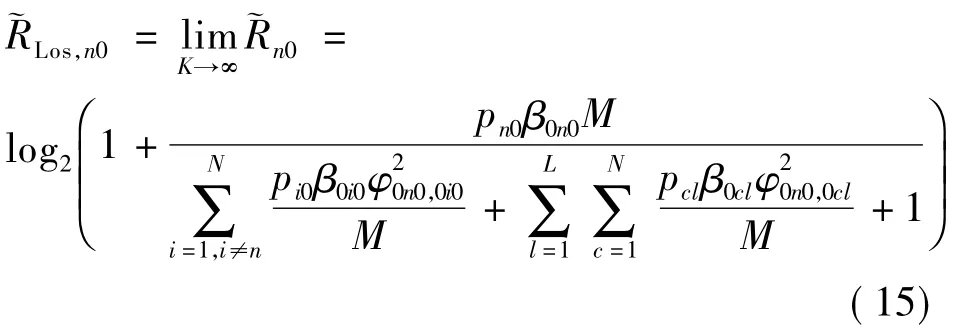
对比式(15)与(13)可以发现,当M较大时,式(15)的数值大于式(13),即用户可达速率会随着LoS径的增强而增加.尽管在形式上式(15)与式(13)存在较大差异,但随着基站天线数目趋于无穷,差异逐渐消失.即各用户采用相同的发射功率,pnl= P/M,当M趋于无穷时,式(15)可记为
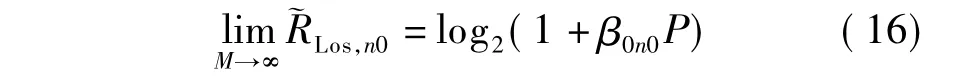
式(16)与式(14)一致,表明在基站天线数目趋于无限大时,瑞利信道和仅包含LoS径的信道拥有相同的可达速率.
3 功率分配
用户可达速率与各用户发射功率相关,增加用户发射功率在增强有用信号的同时会导致用户间干扰的增大,即简单地提高各个用户的发射功率并不能保证用户速率的增长.为了进一步探讨用户发射功率与小区可达和速率之间的关系,本节研究了中心小区功率分配问题,即在满足服务质量要求和总功率受限的条件下,使得小区可达和速率最大.假设中心小区基站已知干扰小区长时信道状态信息与发射功率,相应的优化问题为
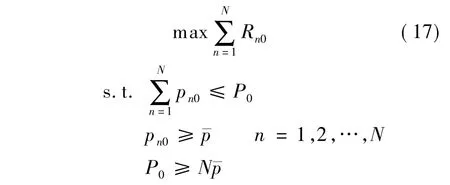
式中,P0为中心小区所有用户总发射功率上限;珔p为满足用户服务质量需求时的最低发射功率; P0≥N珔p表示系统能够让N个用户同时以最低功率珔p进行数据传输.考虑采用MRC接收,用可达速率近似式(12)替换优化问题(17)中Rn0,则功率分配优化目标可以表示为为了便于后续推导,将记为式中,Λ1=2MK0n0+ M + M2(K0n0+1)2,Λ2= (K0n0且Θ需满足


式(19)描述了小区内用户间干扰的2种极限情况:①0表示不存在小区内用户间干扰;②表示小区内每个用户发射功率均为P0.显然,Θ
落在区间内.利用式(19)可得

利用全国网民对淮海经济区5A级景区网络关注度的旅游偏好指数,借助ArcGIS 10.2.2软件,以景区为中心,以几何间隔为分类方法,绘制旅游偏好指数等值线图(图6),分析淮海经济区5A级景区网络关注度的空间分布特征.可以发现,等值线最密集的是位于山东泰安市的泰山景区,旅游偏好最强,且与沂蒙山旅游区、曲阜明故城旅游区距离较近,形成了一个较大的关注度中心;其次是山东枣庄的台儿庄古城景区,与云龙湖景区和连云港花果山景区形成了一个较小的关注度中心.

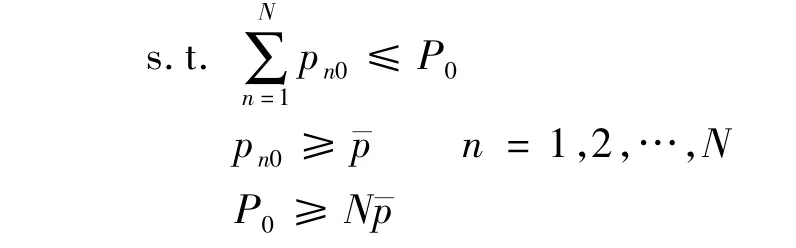
式(21)的解满足

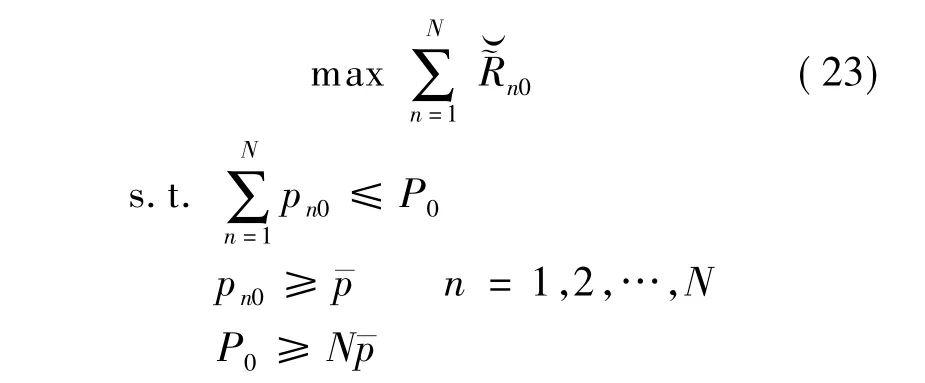
式(23)的解满足
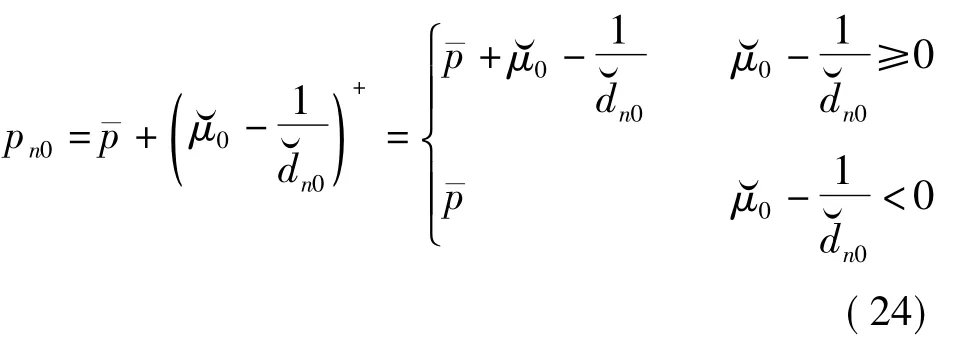
与式(22)的分析一致,式(24)给信道条件好的用户分配更多的发射功率,并且满足M→∞,pn0即在基站天线数目充分大的情况下,基于上界的功率分配算法将会给出对用户进行等功率分配的结果.与式(22)不同,式(24)中与P0无关,导致pn0随着P0的增加而增加,在P0足够大时,各个用户分配到的功率趋于一致.
上述2种算法利用近似和速率的上、下界将功率分配问题简化为利用注水法进行求解的优化问题.与文献[10]提出的利用迭代方式进行功率分配相比,本文所提算法实现简单,可以一次性完成对所有用户的功率分配,并且仅利用到长时信道信息,在显著降低信道估计开销的同时,延长了功率分配的周期.在基站天线数目足够大的情况下,2种算法都会给出等功率分配的结果,表明增加天线数目能够有效降低系统实现复杂度.
4 数值仿真
下面对所提的2种功率分配算法进行蒙特卡洛仿真.仿真场景中,中心小区周围环绕6个干扰小区(L =6),各个小区用户均匀分布在距离各自小区rs=100 m之外、半径rc=1 000 m的六边形小区内.大尺度衰落β0nl= z0nl(r0nl/rh)-v,其中r0nl为小区l中用户n到中心小区基站间的距离,z0nl为阴影衰落,服从标准差为8 dB的对数正态分布,v =3.8为路径损耗指数,小尺度衰落服从瑞利分布.为方便起见,仿真中设置所有用户具有相同莱斯衰落因子K.另外,为了尽可能遍历信道,仿真中产生104次信道,对每次信道下的结果进行平均.
在各个小区总发射功率为10 dB、用户数目为10的仿真参数设置下,中心小区可达和速率与天线数目、莱斯因子的关系见图1.由图可知,蒙特卡洛仿真得到的结果与式(12)得到的结果吻合,表明式(12)为准确近似.与单小区场景相比,多小区场景下的和速率较小,这是因为后者存在小区间干扰.当基站天线数目一定时,小区和速率均随着莱斯因子K的增加而增加,但是单小区场景下的和速率增长更加明显;究其原因在于,小区中各个用户的莱斯因子K相同,K的增加必然导致小区间干扰增加,从而影响了和速率的提升.此外,2种场景下的小区和速率均随着基站天线数目的增加而增加,且增长速率逐渐变缓,这与第2节中的速率分析结果一致.

图1 仿真结果与近似结果比较
根据式(12),不同基站天线数目下中心小区近似和速率与信道莱斯因子的关系见图2.其中,各个小区总发射功率为20 dB,各个小区中用户数目为10.由图可知,当天线数目一定时,小区和速率随莱斯因子的增加而增加,并且在K≥20 dB后达到饱和.这表明当信道莱斯因子超过20 dB时信道快衰落对小区和速率带来的影响可以忽略,即可认为是强LoS径传播环境.

图2 近似和速率与莱斯因子关系
图3给出了中心小区发射总功率和天线数目不同的情况下3种功率分配算法的可达小区和速率比较.其中,各个小区均存在10个用户,中心小区用户最低发射功率珔p =0.5 dB,干扰小区用户发射总功率为10 dB,信道莱斯因子K =6 dB.图中,算法1和算法2分别表示基于上、下界的功率分配算法.由图可知,与等功率分配算法相比,本文提出的2种功率分配算法能够有效提升小区可达和速率,且随着天线数目的增加,和速率增量逐渐减小,这与第3节中的分析结果一致.当中心小区总发射功率为10 dB时,所提的2种功率分配算法性能几乎一致;但是随着发射功率的增加,算法1的性能优于算法2,并且随着天线数目的增加优势更加明显.为了更清晰地反映功率分配带来的性能增益与天线数目、发射总功率之间的关系,定义功率分配相对增益系数η= (CPA-CEQ) /CEQ,其中CPA为采用算法1或算法2得出的小区和速率,CEQ为采用等功率分配算法得出的小区和速率.图4给出了图3对应的η曲线.由图可知,当M =100,P0=10 dB时,所提的2种功率分配算法增益超过25%;当M =100,P0=15 dB时,增益超过15%.这表明在实际系统中,所提功率分配算法能够达到可观的性能增益,然而增益随着功率的增加逐渐减小.

图3 不同功率分配算法下和速率曲线

图4 不同发射功率条件下η曲线
5 结语
本文研究了莱斯信道衰落下,基站采用MRC接收机的多小区massive MIMO系统中的低复杂度功率分配算法.首先,给出了一个高精确度的小区可达和速率近似表达式;然后,基于该近似和速率的上、下界,提出了2种低复杂度的上行功率分配算法.数值仿真表明,在不同的系统参数配置条件下,与等功率分配算法相比,本文所提功率分配算法能够以较低的系统复杂度有效提升小区可达和速率.
参考文献(References)
[1]Telatar I E.Capacity of multi-antenna Gaussian channels[J].European Transactions on Telecommunications,1999,10(6) : 585-595.
[2]Gesbert D,Kountouris M,Heath R W,et al.Shifting the MIMO paradigm[J].IEEE Signal Processing Magazine,2007,24(5) : 36-46.
[3]Marzetta T L.Non-cooperative cellular wireless with unlimited numbers of base station antennas[J].IEEE Transactions on Wireless Communications,2010,9 (11) : 3590-3600.
[4]Ngo H Q,Larsson E G,Marzetta T L.Energy and spectral efficiency of very large multiuser MIMO systems[J].IEEE Transactions on Communications,2013,61(4) : 1436-1449.
[5]Pitarokoilis A,Mohammed S K,Larsson E G.On the optimality of single-carrier transmission in large-scale antenna systems[J].IEEE Wireless Communications Letters,2012,1(4) : 276-279.
[6]Hoydis J,Brink S T,Debbah M.Massive MIMO in the UL/DL of cellular networks: How many antennas do we need?[J].IEEE Journal on Selected Areas in Communications,2013,31(2) : 160-171.
[7]Andrews J G,Buzzi S,Choi W,et al.What will 5 G be?[J].IEEE Journal on Selected Areas in Communications,2014,32(6) : 1065-1082.
[8]Ngo H Q,Larsson E G,Marzetta T L.The multicell multiuser MIMO uplink with very large antenna arrays and a finite-dimensional channel[J].IEEE Transactions on Communications,2013,61(6) : 2350-2361.
[9]Zhang Q,Jin S,Wong K K,et al.Power scaling of uplink massive MIMO systems with arbitrary-rank channel means[J].IEEE Journal of Selected Topics in Signal Processing,2014,8(5) : 966-981.
[10]Fan L X,Huang Y M,Zhang F,et al.Power control and low-complexity receiver for uplink massive MIMO systems[C]/ /IEEE/CIC International Conference on Communications in China.Shanghai,China,2014: 266-270.
Low complexity power allocation algorithms for uplink of massive MIMO systems
Fan Li Jin Shi
(National Mobile Communications Research Laboratory,Southeast University,Nanjing 210096,China)
Abstract:In order to reduce the complexity of the power allocation algorithm for the multi-cell massive multiple-input multiple-output (MIMO) systems in Ricean fading channels,low complexity power allocation algorithms based on the uplink sum rate are proposed.First,in the case of using the maximal-ratio combing (MRC) receiver,an approximate expression of the uplink sum rate and its lower and upper bounds are presented.Then,two power allocation algorithms based on lower and upper bounds respectively are put forward,which satisfies that the total power transmitted by all users is limit and the quality of service of every user is met.These two algorithms only utilizing the long term channel state information such as large-scale fading can reduce the channel estimation overhead and times to perform the power allocation schemes,inducing the reduce of the complexity of system implementation.The simulation results show that,compared with the equal power allocation algorithms,the proposed power allocation algorithms can improve the sum rate significantly with the low signal to noise ratio.However,the higher the signal to noise ratio,the smaller the performance gain.Therefore,the proposed power allocation algorithms can be effectively utilized in the situations with low signal to noise ratio.
Key words:massive multiple-input multiple-output; multi-cell; Ricean fading; maximal-ratio combing;power allocation
基金项目:国家自然科学基金资助项目(61222102)、国家国际科技合作专项资助项目(2014DFT10300).
收稿日期:2015-07-19.
作者简介:范利(1992—),女,硕士生;金石(联系人),男,博士,教授,博士生导师,jinshi@ seu.edu.cn.
DOI:10.3969/j.issn.1001-0505.2016.01.002
中图分类号:TN929.5
文献标志码:A
文章编号:1001-0505(2016) 01-0007-06
