整体架构提前渗透走好规律教学每一步——《乘法分配律》三次教学实践的研究分析

丁水法 倪 芳

第一次实践：从计算到规律的寻找、模型的建构

一、在计算比赛中感受异同、寻找联系

1．比一比，谁算得快。

师：计算比赛，看看哪组算得快？

79×38+21×38

（79+21）×38

反馈结果，讨论顺序，还有什么发现？

2.交换题目再比赛。

（92+8）×56

92×56+8×56

反馈结果，发现什么？

师：选择喜欢的题进行计算，为什么这样挑选？

（80+8）×125

80×125+8×125

36×72+64×72

（36+64）×72

二、在比较研讨中发现等量关系、表达规律模型

比赛时发现了什么？对题目进行分类。

用其他方式表示，尝试用字母写乘法分配律。

指名板书：A×B+C×B=（A+C）×B说说你是怎样想的？A、B、C各代表几呢？

把相等的两个算式用等号连接，这个规律在数学上叫作乘法分配律，用字母表示就是A×B+C×B=（A+C）×B。

三、在巩固练习中加深理解、巩固规律（略）

四、在猜想验证中拓展规律、完整模型结构

师：乘加可以用乘法分配律，那么乘减行吗？

自己举例试一试：100×38-50×38；32×12-29×12。

第二次实践：从生活原型到规律的发现、模型的强化

一、创设情境、生成算式

1.阅读材料，明确主要任务?

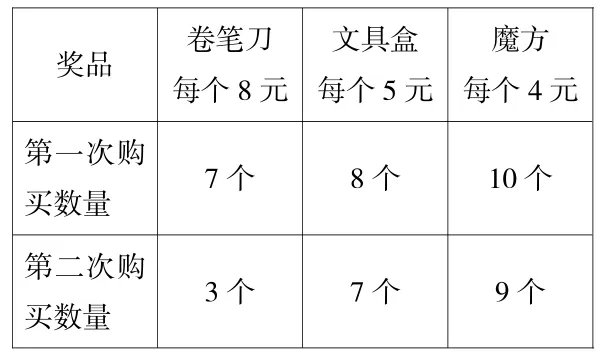
魔方每个4元第一次购买数量 7个 8个 10个奖品 卷笔刀每个8元第二次购买数量 3个 7个 9个文具盒每个5元

2.收集信息，寻找数学问题：买卷笔刀、文具盒、魔方各用多少钱？

3.选择问题，列出综合算式。

4.交流反馈，比较两类不同算式。

二、分类整理，生成模型

1.算式分类，初步感知算式结构?

2.观察算式，寻找两类模型结构。

3.比较结果，发现算式恒等关系：（7+3）×8=7×8+3×8。

4．理解意义，语言表达算式结构：10个8就是“7个8”+“3个8”的和。

5.翻动算式，刺激学生回忆。

6.猜测算式，强化模型结构。

7.总结归纳，初步形成模型。

三、意义建构，理解规律

1.顺藤摸瓜，发现算式。（这样的等式还有吗？写一写、说一说）

2.展开想象，符号表达。（用喜欢的图形表达一般规律）

3.定义规律，规范表达。（用字母（a+b）×c=a×c+b×c，叫做乘法分配律）

四、实践应用，深化吸收。

1.计算比较，选择合适做法。

8×(125+9)和 8×125+8×9

2．抢答比赛，强化简算思想。

7×48+7×52和7×(48+52)

3.回忆旧知，强化模型结构。

回忆长方形周长、两面墙的面积、乘法口诀等。

4.展开想象，寻找其他形式。

（a-b）×c=a×c-b×c

（a+b+n）×c=a×c+b×c+n×c

第三次实践：从数形结合到模型建构

一、复习旧知，铺垫乘法分配律原型

1.用两种方法列出综合算式，算出结果。每组分别完成一题，组内四人先分工后合作，确定汇报人。

（1）计算长方形周长。

（2）计算两幅“点子图”的花朵数量。

（3）计算两堵墙的面积。

（4）计算文具用品的总价。

2.交流汇报。

二、寻找原型，定义乘法分配律概念

1.寻找共同点。

2.总结旧经验。

3.发现一般性。

4.定义乘法分配律

三、算式联想，数形结合促进模型建构

1.把面积计算图用点子图画出来。

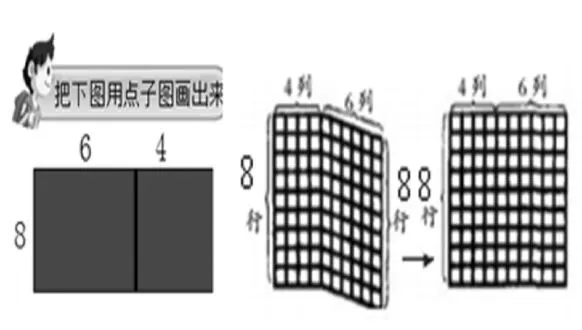
2.看算式编一道求面积的题目。

（34+66）×9=34×9+66×9

四、探究变式，拓展乘法分配律一般性

1.结合图形，用不同方法计算。

2.用字母表达这个算式。

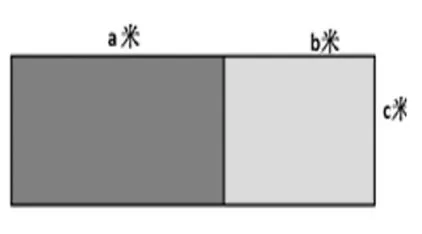
3.看算式说一说箭头表示意义。

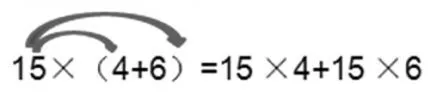
【三次实践后的思考分析】

一、系统把握教材，整体呈现学生的经验水平，铺垫定律模型

1.准备阶段铺垫好基础知识，在前期学习中累积经验。

在教学表内乘法、两位数乘一位数、周长、面积等时有意渗透。

2.定义阶段搭建好模型框架，在回忆辨识中理解定律。

在四年级教学乘法分配律时，再次借助周长、面积及点子图帮助理解算例，回忆中逐步建立数形模型。

3.内化阶段利用好字母表达，在思维回传中深化概念。

三个作用：一是方程思想的渗透，二是乘法分配律模型化的重要基础，三是符号化思想的重要渗透。

二、注重数形结合，提炼生活原型的具体方法，加深意义理解

1.提前“塑型”，在生活中寻找定律“痕迹”。二年级时渗透，既帮助理解口诀，又逐渐建立乘法分配律的初步模型，还促进思维展，累积数形结合思想。善用点子图，提前为后继知识“塑型”。完整“构型”，在数形中加深对意义的理解。完整教学时把原型再次呈现：口诀、笔算乘法、周长、面积教学等，然后转化到点子图和面积图，让学生在回忆时构建好“型”，从而进一步理解的算理。

2.转化“定型”，在转化中准确理解概念。如下图这样的模型转化器刚好是非常适合学生操作和理解。

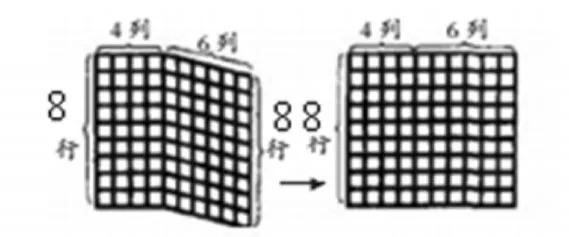
三、提前定律教学，为思维训练打下算理基础，促进思维发展

1.提前教学乘法定律，让学生早日找到简算依据。根据我们近几年对乘法分配律教学的研究，我们认为学生对于乘法分配律学得尚不扎实的最主要原因有以下几个：（1）教师教学中忽视了教材定律的“原型”挖掘和学生需要的“活动经验”渗透。（2）教材编排中定律教学序列安排存在一定的问题。笔者以为，我们要适当提前定律教学。

2.放大简算思维训练，让学生简算思维更加宽广。在教学乘法分配律之后，《两位数乘两位数》章节先进行乘法分配律笔算教学，后再放大简算思维训练。