探根求源顺势而导——《认识负数》教学设计与解读

苏陈林

（本文作者系朱乐平数学名师工作站“一课研究”组成员）

【教学内容】

人教版六年级下册第2～4页例 1、例2。

【教学目标】

1.在熟悉的生活情境中认识负数，能正确地读、写正数和负数。

2.通过多元表征理解负数的意义，体会正数和负数可以表示两种相反意义的量。

3.感受正、负数和生活的密切联系，初步学会用负数表示一些日常生活中的实际问题。

【教学过程】

一、激活旧知，引出负数

师：同学们，我们从小学一年级开始至今，已经认识了很多数，你能举例说说吗？（板书：数）

预设：整数、小数、分数、百分数、负数等。

师：今天这节课我们就来认识新的朋友“负数”。（板书课题“认识负数”）

【解读：课始便开门见山提出“负数”一词，从数的大背景切入，和学生一起回顾学过的数，激活学生已有的知识经验，以“类属”的方式直接揭题，引导学生初步感知数系的扩张。把“负数”的教学放在整个数的体系中进行，不仅仅是对“数的认识”的一种简单的框架式梳理，也是引导学生对认数系统进行重构的过程。】

二、联系生活，感知负数

师：生活中，你在哪里见过负数？

学生举例，根据举例相应地出示生活中的负数图。（图略）

在列举中认识负号，尝试读写负数。

【解读：从生活中引出负数，引导学生初步感知负数，为学生接下来进一步认识负数做好铺垫。】

师：结合自己的生活经验说说这些负数都表示什么意思？

（出示没有0刻度的温度计，尝试找零下5摄氏度）

【解读：对于学生来说，在温度计上找零下5摄氏度是困难的。为什么困难？因为没有相对应的量，没有可参照的刻度，找出来的必然没有统一的答案，由此引发学生认知上的矛盾，进一步体会负数与“相反意义的量”之间的关联。】

课件出示：有0刻度的温度计。“现在你能找到零下5摄氏度了吗？”“为什么还不行？”（因为没有出现单位刻度）出示单位刻度-1。那现在呢？一个单位一个单位地数下来，从“-1”数到“-5”。

【解读：在这个环节中，出示“0刻度”意味着“标准量”的出现。两次认知冲突，引导学生进一步体会作为标准量对于负数的重要性。数学概念的理解在两次追问中逐渐清晰。】

三、以练促思，理解相反意义

1.在刚才的温度计上找到零上5℃（课件直接跳到+5），用什么符号表示？（+5）怎么写怎么读呢？认识正数和正号。

追问：“你是怎么想的？”

2. 课 件 出 示 +1、+2、+3，+4。这些数又是什么数呢？（正数隐去正号）现在呢？还是正数吗？表示什么？

追问：“负号呢，能省略吗？为什么？”比对一下刚才的零下5℃（-5℃）和现在的零上5℃（+5℃），你有什么发现？

引导发现：正号可以省略不写，负号不能省略。+5和-5到0的距离相同、方向相反。

【解读：负数的产生是“数”的数学化的一个过程，也是用数学符号记录现实生活中特定数量的一个过程。带有负号的数是负数，描述的是负数的外部特征，并不是它的本质意义。负数的本质意义应该与正数结合起来理解，因为负数与正数是具有相反意义的两种量，它们之间其实是一种辨证的关系。】

3.反馈练习：在刚才的温度计上表示出三个城市的气温。

师：通过刚才的练习你发现了什么？（小结：零上温度都是正的，在0上面，零下温度都是负的，在0下面）

4.在数轴上感知0对于正负数的价值。

（1）0℃的认识。零上温度可以用正数来表示，零下温度可以用负数来表示，那0℃呢？（淡水开始结冰的温度，零上温度和零下温度的分界点）

（2）0在数轴上的对应。数形结合，将温度计转化为数轴（竖直变水平）。从0℃到数轴上的0刻度。找5℃和-5℃在数轴上的对应位置。

（3）扩大数轴上其他数的对应。继续找其他相对应的点（从整数到小数到分数，从正数到负数），结合生活情境再次说说各点分别表示什么意思。

归纳小结：0既不是正数也不是负数。如果过去我们所认识的数只分为正数和0的话，那么今天我们可以对“数”进行重新分类：

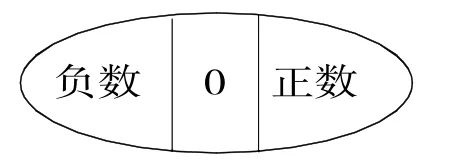
【解读：在正负数学习中，0是它们的分界点。通过呈现温度计上的0、数轴上的0等数学问题，引导学生理解正负数的分界点。在没有零刻度的温度计上找出某个温度，学生可以体会到：只有找到分界点（0），才能找出正负数，加深了对0的认识。将具体的负数和抽象的数轴上的数一一对应，对于学生来说是之前在数轴上表示分数、小数、整数这些直观模型的进一步延伸。由温度计到数轴，正负数的学习经历着生活到数学、具体到抽象的过程，学生在逐层抽象中实现了数学思维的飞跃。】

四、练思结合，促进建构

1.读出下列各数，并指出哪些是正数，哪些是负数。

-7，2.5，0，-5.2，+41。

2.在空白处填上合适的数。

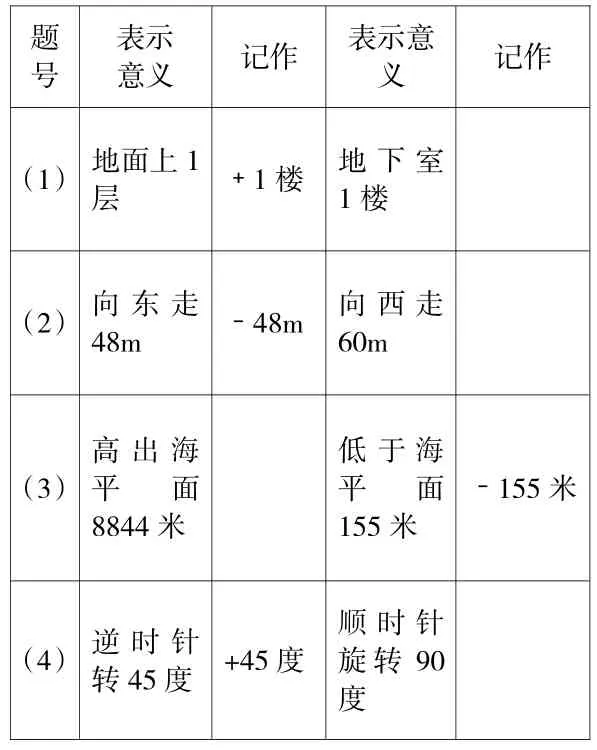
题号表示意义 记作 表示意义 记作（1） 地面上1层 ﹢1楼 地下室1楼（2） 向 东 走48m ﹣48m 向西走60m（3）高出海平 面8844米低于海平 面155米﹣155米（4） 逆 时 针转45度 +45度顺时针旋转90度

【解读：在练习中把生活中的素材整合到一张表格里，然后在分析的过程中突出相反意义的量，进一步加深了学生对负数本质的理解。】

3.运动中的正负数。

刘翔在第十届世界田径锦标赛半决赛中，110米栏的成绩是13.42秒，当时赛场风速为每秒-0.4米。小组讨论：风速怎么还有负的？

4.挑战题。

温度计从5（－5）摄氏度，上升6个单位、下降6个单位各是多少？

【解读：通过解决挑战性问题，学生加深了对负数意义的理解。同时，也丰富拓展学生对负数外延的认识，拓展了学生对正数与零的意义建构，尤其是随着基准线的变化(零刻度)，相应的数也在变化，让学生深刻体会到正数、负数基于零的相对性，进一步提升了学生思维的灵活性。】

五、总结全课，延伸拓展

师：这节课我们认识了负数，其实我国很早就有了负数的表示方法，请看。

课件出示：历史上负数的表示方法。

师：对于今天这节课，你有什么新的感受，你印象最深的是什么？还有什么问题？

小结：今天只是一个良好的开端，负数以后我们还会继续深入学习，生活中还有更广泛的应用；走进负数，还有更多的知识等待我们去探索，相信同学们在今后的生活和学习中会有更多的收获。

【解读：梳理本节课所学的知识，引导学生用数学的眼光观察生活、走进生活，去发现更多更有趣的数学知识。这样教学，起到了探根求源、顺势而导的有效作用，学生对数的认识形成了一个比较完整的认知结构，也为进一步学习数学知识打下了基础。】