端叠氮聚叠氮缩水甘油醚的热分解动力学
2016-05-08董军欧江阳
董军, 欧江阳, 朱 林, 李 彬
(泸州北方化学工业有限公司, 四川 泸州 646605)
1 引 言
叠氮聚醚类含能增塑剂(GAPA)是含有烷基叠氮基团的端叠氮脂肪族聚醚含能增塑剂,因其具有生成热高、密度大、燃气无腐蚀性、氮含量高、改善能量释放特性等优点[1],主要用于火箭推进剂、烟火剂和高聚物黏结炸药(PBX)中。为了更好地研究GAPA推进剂性能,需要对GAPA在温度升高时的热分解反应历程有一个较为清楚的认识,目前国内外应用多种方法进行了广泛的实验及理论计算研究[2-4]。王刚[5]等采用TG/DSC-IR-MS联用技术对GAPA及其增塑聚P(BAMO/AMMO)的热分解特性进行研究,GAPA、GAPA/ P(BAMO/AMMO)的热分解主要经历两个阶段,即叠氮基团的分解和聚醚主链的分解,GAPA可以降低P(BAMO/AMMO)的分解温度,并且能提高体系表观分解热。徐若千[6]等合成了三臂型叠氮含能增塑剂GAPA,并采用DSC和TG对GAPA进行了热分解研究,表明GAPA是一种性能优良的齐聚物含能增塑剂。但是有关GAPA的热分解动力学过程尚未见报道。为此,本研究采用TG-DSC联用技术对GAPA热分解规律进行了研究,并在此基础上研究了GAPA热分解特性、机理函数、动力学方程、热力学参数和热安定性参数,为深入研究GAPA推进剂热安定性和高温下燃烧性能奠定了基础。
2 实验部分
2.1 样品的制备
GAPA为实验室自制样品,其制备方法如图1所示。采用三步合成法,以乙二醇为起始剂,三氟化硼为催化剂,环氧氯丙烷为单体进行聚合反应,合成出高分子聚合物(PECH-OH),经磺酸酯化、叠氮化后合成出端叠氮聚叠氮缩水甘油醚(GAPA)[7]。GAPA为淡黄色粘性液体,数均分子量810(GPC),羟值2.95 mgKOH·g-1,纯度97.8%,密度1.27 g·cm-3,水分0.04%。元素分析(C23H39N24O2,%): 理论值(实测值)C 34.33(35.06),H 4.8(4.89),N 41.79(46.15)。

Scheme1Synthetic route of GAPA[7]
2.2 仪器和实验条件
差示扫描量热(DSC)分析: DSC 200 F3型差示扫描量热仪,德国耐驰公司。样品质量为0.5~1.0 mg,升温区间为-70~400 ℃,升温速率分别为2,5,10,20 ℃·min-1,动态氮气气氛,流速为30 mL·min-1, 试样皿为铝盘。
热重(TG)分析: TG 209 F3型热重分析仪,德国耐驰公司。样品质量为0.5~1.0 mg,升温区间为30~400 ℃,升温速率为2,5,10 ℃·min-1,动态氮气气氛,试样皿为铝盘。
3 结果与讨论
3.1 GAPA热分解特性
3.1.1 DSC分析结果
GAPA在不同升温速率下(2,5,10,20 ℃·min-1)的DSC曲线如图1所示。由图1获得GAPA热分解的特征参数见表1。

图1不同升温速率下GAPA的DSC曲线
Fig.1DSC curves of GAPA at different heating rates
表1不同升温速率下GAPA的DSC结果
Table1DSC results of GAPA at different heating rates

β/℃·min-1Ts/℃Tp/℃Te/℃Tg/℃ΔHd/J·g-12173.87229.90257.90-61.3485995184.73237.23269.72-60.06833610192.61245.10282.60-59.90822920211.78251.78286.78-40.725832
Note:βis heating rate;Tsis start decomposition temperature;Tpis exothermic peak temperature;Teis end decomposition temperature;Tgis glass trastion temperature; ΔHdis decomposition enthalpy.
从图1可以看出,GAPA的DSC曲线均为单峰,当升温速率为10℃·min-1时整个放热过程发生在207.6~276.8℃。随着升温速率的增加,DSC曲线的放热峰向高温方向移动,放热峰温和放热量逐渐增大,当升温速率为20℃·min-1时DSC曲线峰温最大,峰形最尖,放热速率最快,这可能是因为GAPA放热速率随着升温速率的增大而增大。
3.1.2 TG分析结果
GAPA在升温速率分别为2,5,10 ℃·min-1时的TG曲线见图2,升温速率为5 ℃·min-1时的TG-DTG曲线见图3。
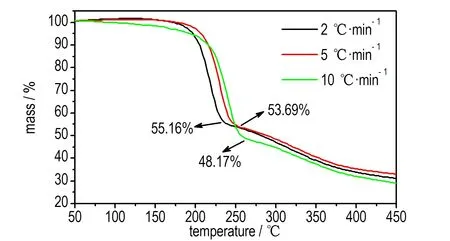
图2不同升温速率下GAPA的TG曲线
Fig.2TG curves of GAPA at different heating rates
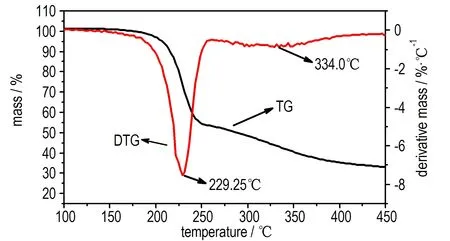
图35 ℃·min-1时GAPA的TG-DTG曲线
Fig.3TG-DTG curves of GAPA at 5 ℃·min-1
从图2和图3可知,不同升温速率下GAPA的TG曲线趋势相似,GAPA加热到约200 ℃才有较明显的质量损失,GAPA的热分解过程包括两个阶段。第一阶段为放热分解阶段,温度区间为188~248 ℃,质量损失为44.8%~51.8%,DTG峰温为229.25 ℃,该阶段为叠氮基团的热分解所致[7],这与GAPA的氮含量46.15%结果一致; 第二阶段为GAPA骨架裂解阶段,温度区间为248~400 ℃,质量损失为25%,DTG峰温为334.0 ℃,该阶段为碳、氢等的分解,没有明显的放热效应; 当温度加热到400℃时,失重百分数随温度的升高而不再变化,未再有质量损失。
3.2 动力学参数计算
3.2.1 Kissinger法
根据GAPA在升温速率2,5,10,20 ℃·min- 1时DSC曲线的峰温,用Kissinger法[8]通过线性回归求得热分解动力学参数。
(1)
式中,βi为试样升温速率,℃·min-1;Tpi为DSC曲线上的第一个峰温,K;EK为表观活化能,J·mol-1;AK为指前因子,s-1;R为理想气体常数,8.314 J·mol-1·K-1。由lnβi/Tpi2-1/Tpi的关系,经回归分析求得GAPA的表观活化能EK=218.47 kJ·mol-1,AK=1.06×1022s-1,其中线性回归相关性为0.99791,标准偏差为0.07491。
3.2.2 Ozawa法
通过不同升温速率下的TG曲线用非等温法进行热分解动力学研究时,常用的Ozawa公式[9]为:
(2)
式中,β为试样升温速率,℃·min- 1;A为指前因子,s-1;Ea为表观活化能,J·mol-1;R为理想气体常数,8.314 J·mol-1·K-1;T为温度,K;α为反应深度;F(α)为机理函数的积分形式。由lnβi-1/Tpi的关系,经回归分析求得GAPA的表观活化能EO=215.87 kJ·mol-1,其中线性回归相关性为0.99807,标准偏差为0.03246。
如果选择相同的α,lgβ与1/T呈线性关系,由直线的斜率计算活化能,并用来求解热分解的机理函数。
根据Doyle法[9],(2)式可变换为:
(3)
对任何热分解机理函数,lgF(α)与1/T呈线性关系。对某个假设的反应机理函数,若通过Doyle法求得的热分解活化能与Ozawa法求得的活化能接近,且线性相关系数好,则可由此获得最可几热分解反应机理函数。
本实验的升温速率为2,5,10 ℃·min-1,升温的温度区间为30~400 ℃。从TG曲线对应的失重台阶来看,GAPA热分解主要分为两个阶段,分别位于反应深度为0.10~0.45和0.45~0.75。对于热分解的第一阶段(0.10~0.45),根据GAPA的热重曲线求出反应深度分别为0.10,0.15,0.20,0.25,0.30,0.35,0.40,0.45时所对应的分解温度T。根据公式(2)和试验数据对lgβ与1/T进行线性拟合,由直线斜率获得表观活化能Ea,计算结果见表2,线性拟合结果见表3。
表2由Ozawa法得到的GAPA热分解反应活化能(α=0.10~0.45)
Table2Activation energy of the thermal decomposition reaction in the range of 0.10~0.45 of GAPA obtained by Ozawa′s method

αT/℃β=2℃·min-1β=5℃·min-1β=10℃·min-1Ea/kJ·mol-10.10205.59216.77215.63209.180.15209.63221.86224.81183.680.20213.61224.38229.98186.470.25217.76228.01233.0202.220.30219.56231.61237.81171.760.35223.49235.05241.39178.590.40227.44238.60244.72187.70.45239.47250.83248.02225.16average193.09
表3lgF(α)与1/T线性拟合结果(α=0.10~0.45)
Table3Liner fitting result of lgF(α)-1/T in the range of 0.10~0.45

β/K·min-1doylemethodinterceptsloper2Ea/kJ·mol-1A/s-1Ea/kJ·mol-1218.9775-10069.55390.9389183.311.78×1017519.4147-10521.36420.9374191.541.16×10181020.3164-11052.46200.9978201.201.77×1019average192.012.95×1019193.09
对30种热分解反应机理函数的相应lgF(α)与1/T进行线性回归分析,线性拟合结果表明: 对于GAPA的热分解,在反应深度为0.10~0.45阶段的热分解属于随机成核和随后生长,属于第2号函数,其积分形式为F(α)=α+(1-α)ln(1-α),反应机理的微分形式为f(α)=-[ln(1-α)]-1,表观活化能Ea为192.01 kJ·mol-1,指前因子A为2.95×1019s-1,热分解动力学方程为:

(4)
同理,采用Ozawa法对第二个阶段(α=0.50~0.65)进行表观活化能的计算,根据GAPA的热重分析曲线求出反应深度分别为0.50,0.55,0.60,0.65时所对应的分解温度,计算结果见表4,线性拟合结果见表5。
表4由Ozawa法得到的GAPA热分解反应活化能(α=0.50~0.65)
Table4Activation energy of the thermal decomposition reaction in the range of 0.50-0.65 of GAPA obtained by Ozawa′s method
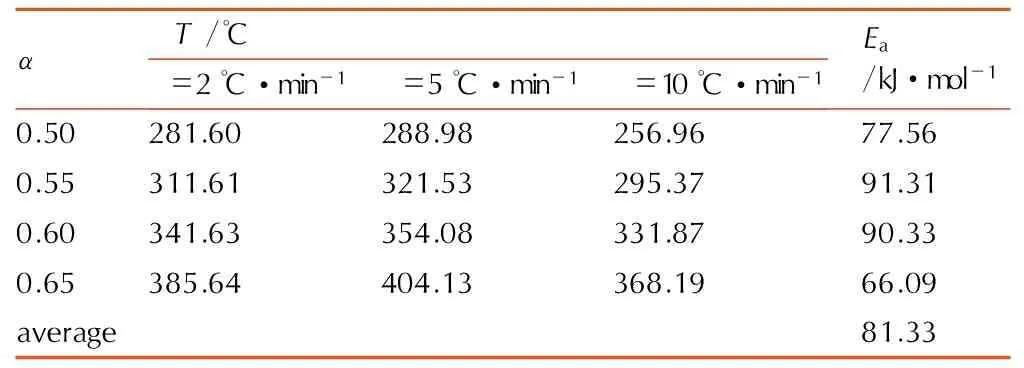
αT/℃β=2℃·min-1β=5℃·min-1β=10℃·min-1Ea/kJ·mol-10.50281.60288.98256.9677.560.55311.61321.53295.3791.310.60341.63354.08331.8790.330.65385.64404.13368.1966.09average81.33
线性拟合结果表明,在反应深度为0.50~0.65阶段的热分解属于随机成核和随后生长,n=4机理,属于第13号函数,其积分形式为F(α)=[-ln(1-α)]4,反应机理的微分形式为f(α)=(1/4)(1-α) [-ln(1-α)]-3,表观活化能Ea为43.44 kJ·mol-1,指前因子A为8.72×1012s-1,热分解动力学方程为:
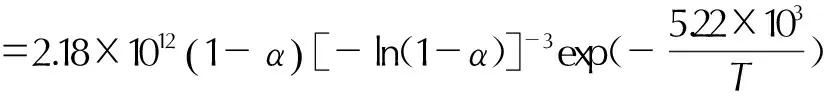
(5)
3.3 热力学参数计算
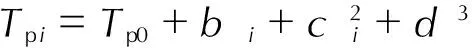
表5lgF(α)与1/T线性拟合结果(α=0.50~0.65)
Table5Liner fitting result of lgF(α)-1/Tin the range of 0.50~0.65

β/K·min-1doylemethodinterceptsloper2Ea/kJ·mol-1A/s-1Ea/kJ·mol-123.97792-2554.565470.9982846.503.85×101253.65407-2405.485250.9977443.796.22×1012103.49702-2199.482840.9981440.041.61×1013average43.448.72×101281.33
GAPA在Tp0时热力学参数反应的活化熵(ΔS≠)、活化焓(ΔH≠) 和活化自由能(ΔG≠)由式6、7、8求得[9]。
(6)
ΔH≠=EK-RTp0
(7)
ΔG≠=ΔH≠-Tp0ΔS≠
(8)
式中,kB为Boltzmann常数,1.381×10-23J·K-1;h为Planck常数,6.626×10-34J·s;R为气体常数,8.314 J·mol-1·K-1;Ak为指前因子,1.06×1022s-1;Ek为表观活化能,218.47 kJ·mol-1
计算GAPA可得分解反应的活化自由能ΔG≠=132.76 kJ·mol-1,活化焓ΔH≠=214.34 kJ·mol-1以及活化熵ΔS≠=164.21 J·mol-1·K-1。
3.4 热安全性参数计算
根据GJB772A-1997方法505.1中的Zhang-Hu-Xie-Li法[10],按下式计算自发火温度:
(9)
式中,EK为表观活化能,J·mol-1;R为气体常数,8.314 J·mol-1·K-1;Tp0为加热速率趋于零时的外推峰温,K;Tbpo为Zhang-Hu-Xie-Li法处理得到的自发火温度,K。将EK和Tbpo代入(10)式中,计算得到Tbpo=506.55 K。
根据文献[11],自加速分解温度可按下式计算:
(10)
式中,TSADT为自加速分解温度,K;Tbpo,EK如式(9)。将EK及Tbpo带入(10)式中,计算可得TSADT=496.78 K。
4 结 论
(1)GAPA热分解经历两个阶段,第一阶段为叠氮基团热分解阶段,温度区间为188~248 ℃,质量损失为44.8%~51.8%,DTG峰温为229.25 ℃; 第二阶段为骨架裂解阶段,温度区间为248~400 ℃,质量损失为25%,DTG峰温为334.0 ℃,没有明显的放热效应。


(3)由非等温DSC曲线通过Kissinger法计算得到动力学参数,其中活化能EK为218.47 kJ·mol-1,指前因子AK为1.06×1022s-1。
(4)由Zhang-Hu-Xie-Li法计算出GAPA热力学参数,其中自发火温度Tbpo为506.55 K,自加速分解温度TSADT为496.78 K,以及活化自由能(ΔG≠)、活化焓(ΔH≠)和活化熵(ΔS≠)分别为132.76 kJ·mol-1、214.34 kJ·mol-1和164.21 J·mol-1·K-1。
参考文献:
[1] 王平, 郁卫飞, 刘春. 支化聚叠氮缩水甘油醚硝酸酯的制备[J]. 含能材料, 2008, 16(6):395-397.
WANG Ping, YU Wei-fei, LIU Chun.Preparation of branched glycidyl azide polymer nitrate[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2008, 16(6): 395-397.
[2] Farber M , Harris S P, Srivastava R D. Mass spectrometric kinetic studies on several azido polymers[J].CombustionFlame, 1984, 55(84): 203-211.
[3] Haas Y, Ben Eliahu Y, W elner S. Welner infrared laser induced decomposition of GAP[J].CombustionFlame, 1994, 96(3) : 201-211.
[4] Tang C J, Lee Y J, L itzinger T A. Simultaneous temperature and species measurements of the glycidyl azide polymer (GAP) propellant during laser induced decomposition [J].CombustionFlame, 1999, 117: 244-256.
[5] 王刚, 葛震, 李霄羽, 等. GAPA及GAPA/P(BAMO/AMMO)含能热塑性弹性体的热性能[J]. 中国科学: 化学, 2015, 45(7): 719-724.
WANG Gang, GE Zhen, LI Xiao-yu, et al. The thermal property of GAPA and GAPA/P(BAMO/AMMO)[J].ScienceChinaChemistry, 2015, 45(7): 719-724.
[6] 徐若千, 姬月萍, 丁峰, 等. 三臂型叠氮含能增塑剂GAPA的合成与性能[J]. 含能材料, 2009, 17(6): 681-684.
XURuo-qian, JI Yue-ping, DING Feng, et al. Synthesis and Properties of Tri-arms glycidyl azide polymer azide[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2009, 17(6): 681-684.
[7] 王晓, 罗运军, 柴春鹏. 端叠氮基聚叠氮缩水甘油醚的合成与热性能[J]. 火炸药学报, 2010, 33(6): 57-60.
WANG Xiao, LUO Yun-jun, CHAI Chun-peng. Synthesis and thermal Property of azido-terminated glycidyl azide polymer[J].ChineseJournalofExplosives&Propellant, 2010, 33(6): 57-60.
[8] Kissinger H E. Reaction kinetics in differential thermal analysis [J].AnalyticalChemistry, 1957,29(11): 1702-1706.
[9] 何志伟, 高大元, 刘祖亮. 2,6-二氨基-3,5-二硝基吡啶-1-氧化物及其黏结炸药的热分解动力学[J]. 火炸药学报, 2009, 32(2): 32-35.
HE Zhi-wei, GAO Da-yuan, LIU Zu-liang. Thermal decomposition kinetics of 2, 6-diamino-3, 5-dinitropyridine-1-oxide and its formulation explosives[J].ChineseJournalofExplosives&Propellant, 2009, 32(2): 32-35.
[10] 胡荣祖,史启祯. 热分解动力学[M]. 北京: 科学出版社, 2001: 127-131.
HU Rong-zu, SHI Qi-zhen. Thermal analysis kinetics[M]. Beijing: Science Press, 2001: 127-131.
[11] 汤崭, 杨利, 乔小晶, 等. HMX热分解动力学与热安全性研究[J]. 含能材料, 2011, 19(4): 396-400.
TANG Zhan, YANG Li, QIAO Xiao-jing, et al. On thermal decomposition kinetics and thermal safety of HMX[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2011, 19(4): 396-400.
