3,4-二硝基呋咱基氧化呋咱冷却结晶动力学

侯 欢, 王建龙, 曹端林, 周彦水, 陈丽珍, 兰贯超

(1. 中北大学化工与环境学院, 山西 太原 030051; 2. 西安近代化学研究所, 陕西 西安 710065)

1 引 言

3,4-二硝基呋咱基氧化呋咱(DNTF)是一种新型高能量密度材料,具有爆速高、密度大、熔点低等优点,可作为炸药和推进剂的成分[1-4],具有广阔的应用前景。含能材料的晶体颗粒品质对其机械强度、感度和输出能量都有影响。结晶过程中,溶剂的选择、结晶温度、过饱和度、搅拌强度等外部因素都会影响晶体的生长。为了进一步提高DNTF的晶体品质,需要通过重结晶过程控制晶体形貌。然而自DNTF合成以来,研究工作主要是围绕其合成工艺和应用进行,对其结晶过程的研究刚刚起步,目前还没有形成成熟工艺,因此需要对DNTF的结晶动力学进行研究。

结晶动力学是工业结晶过程分析、设计、优化及操作的重要依据,也是决定晶体产品粒度分布以及产品质量的重要因素,为结晶操作和结晶器设计放大提供必不可少的数据[5],它与分子动力学、流体力学等一起共同形成了工业结晶过程模拟及产品晶形预测的基础[6]。结晶动力学研究包括成核动力学和生长动力学两部分,其中晶体生长模式的确定是结晶动力学方程研究的一大难题。目前对晶体生长与粒度的关系已进行了大量研究,如晶体生长与粒度无关的ΔL定律、ASL模型、晶体生长速率与粒度呈幂指数的函数关系[7-9]以及其他生长形式[10-11]。Tavare[12]等人研究了结晶动力学测定方法和动力学数据处理方法。

本研究采用间歇动态法,对DNTF在V(乙酸)∶V(水)=7∶3的混合溶液中进行冷却结晶动力学研究。目前国内外只有关于DNTF在不同溶剂中溶解度和结晶相关文献报道[13-15],因此本研究依据粒数衡算原理,通过测定DNTF结晶动力学数据,利用最小二乘法回归由实验所得的数据,确定DNTF冷却结晶的成核和生长速率方程,为DNTF的结晶工艺优化及工业放大提供基础数据。

2 理论基础

2.1 晶体成核与晶体生长

结晶过程中,成核是晶体生长过程必不可少的核心,其成核速率是决定产品粒度分布的首要因素,并且成核机理还是影响产品纯度、聚集情况和外观形状的主要因素之一。成核过程在理论上可分为两大类:初级成核和二次成核。在绝大多数工业结晶器中,二次成核过程不能忽略,晶体成核速率可用如下的经验方程来表示[16]:

(1)

式中,Bs为二次成核速率,m-3·s-1;kb为与温度有关的成核速率常数;MT为悬浮密度,g·mL-1;ωr为比功率输入,W·m-3,如果系统有搅拌则为搅拌强度;S为过饱和比;i,j,b为常数,受操作条件的影响。

晶体生长是扩散和结合的过程,根据晶体生长速率与粒度的关系可分为粒度无关生长和粒度相关生长。不考虑晶体破碎、聚集的情况下,采用粒度无关生长模型,其线性生长速率可以用如下经验方程来表示[16]:

(2)

式中,G为生长速率,μm·s-1;kg为生长速率常数;Ea为生长活化能,J·mol-1;R为摩尔气体常数,8.314 J·mol-1·K-1;T为结晶温度,℃;S为过饱和比。

2.2 粒数衡算方程

粒数衡算方程是结晶过程的基本衡算方程之一,最早由Randolph和Larson提出[17],也称粒数连续性方程。通用的粒数衡算方程为:

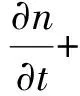
(3)

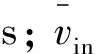
对于没有进出料且忽略聚集、破碎等二次过程的间歇结晶过程,如果结晶器中粒子混合均匀,则粒数衡算方程可写为:

(4)

间歇动态法确定动力学参数方法很多,其中应用较多的是分离变量法和分级法[18]。从分离变量法中可知,对于粒度无关生长模型,反映在粒数密度函数曲线上,lnn与L为线性关系。

3 实验部分

3.1 材料及仪器

DNTF,重结晶后纯度大于99.5%,西安近代化学研究所; 冰乙酸,分析纯,纯度大于99.5%,国药集团化学试剂有限公司; 蒸馏水,实验室自制。

电子天平,±0.0001 g,梅特勒-托利多仪器有限公司; 夹套结晶器,500 mL,太原迎新街玻璃仪器厂; 恒温水浴锅,±0.01 ℃,巩义市予华仪器有限责任公司; 电动搅拌器,上海申生有限公司; 激光粒度仪,丹东百特; 真空干燥箱,巩义英峪豫华,温度计,北京中西远大科技有限公司; 移液管,太原迎新街玻璃厂; He-Ne激光器,北京大学物理系; 取样器,太原迎新街玻璃厂; 微型过滤器,东莞市菲迪五金制品有限公司。

3.2 试验装置

DNTF间歇冷却结晶过程动力学研究的实验装置如图1所示,该装置主要由结晶器、搅拌系统、温控系统及取样系统组成。

图1 结晶动力学实验装置示意图

1—电热恒温水浴锅, 2—冷凝管, 3—结晶器, 4—取样口, 5—水银温度计, 6—电动搅拌器, 7—搅拌器控制器

Fig.1 Schematic diagram of the measurement setup of crystallization kinetics

1—electric heated water bath, 2—condenser pipe, 3—mold, 4—sampling port, 5—mercury thermometer, 6—electromagnetic stirrer, 7—stirrer controller

3.3 实验过程3.3.1 溶解度和介稳区测定

本研究采用激光动态法[19],测定DNTF在V(乙酸)∶V(水)=7∶3的混合溶液中的溶解度和超溶解度[15],介稳区测定过程中,结晶工艺条件为冷却速率0.1 K·min-1,搅拌速率300 r·min-1。

3.3.2 结晶动力学测定

在间歇结晶器中研究DNTF的冷却结晶动力学,具体实验步骤如下:

安装好实验装置,准确称取DNTF和量取溶剂,加入到结晶器中,本研究采用500 mL四口烧瓶作为结晶器,加料量300 mL,开启水浴装置温度控制系统,在预定起始温度下搅拌30 min,配制起始温度下的饱和溶液; 按预定降温速率开始降温,到一定温度时加入一定量的晶种(80～140目),晶种量为起始DNTF质量的1%～3%,并且养晶30 min; 继续按预定降温速率降温,直到结晶过程结束。

从养晶后开始降温起,每隔10 min用取样器抽取约3 mL晶浆样本,迅速抽滤,并将滤饼烘干并准确称量,记录晶浆样本体积和干燥的滤饼质量,计算悬浮密度。再将滤液蒸发得到溶质并干燥,准确称出干燥晶体的质量,计算溶液密度。将干燥晶体分散于去离子水中,测定晶体粒度分布(CSD)。

按预定的动力学实验方案(表1),改变DNTF质量、结晶起始温度、搅拌速率和降温速率,重复上述实验。

表1 冷却结晶动力学实验安排表

Table 1 Experiment scheme of cooling crystallization kinetics

No．m(DNTF)/gcrystallizationtemperature/Kseedjointemperature/Kstirringrate/r·min-1coolingrate/K·min-1121．0338．15333．153000．2221．0338．15333．155000．3321．0338．15333．154000．3416．5333．15328．153000．3516．5333．15328．154000．2616．5333．15328．155000．2712．6328．15323．153000．1812．6328．15323．155000．1912．6328．15323．154000．1

4 实验结果与讨论

4.1 DNTF在V(乙酸)∶V(水)=7∶3的混合溶液中的溶解度和介稳区

实验测定的DNTF在V(乙酸)∶V(水)=7∶3的混合溶液中的溶解度曲线和介稳区如图2所示。

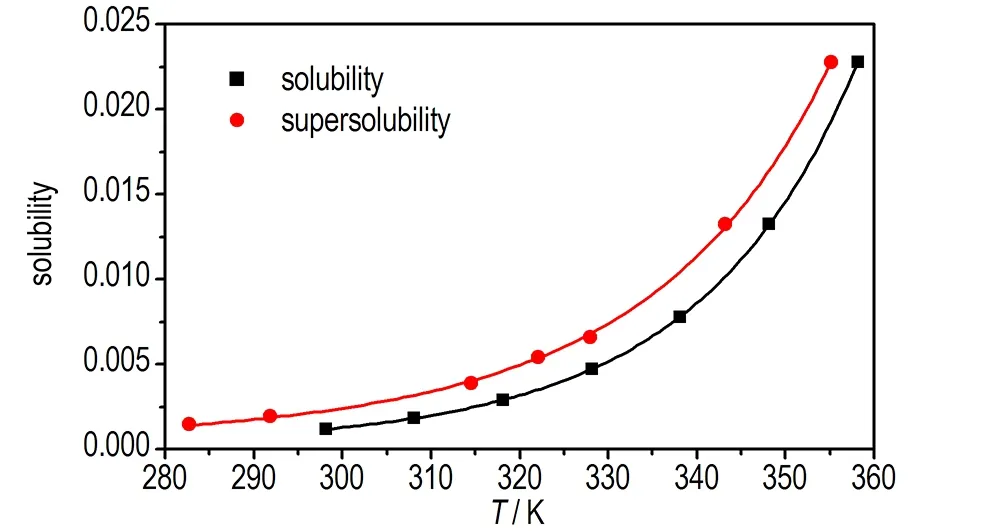
图2 DNTF在V(乙酸)∶V(水)=7∶3的混合溶液中的溶解度及介稳区

Fig.2 The solubility and metastable zone of DNTF inV(acetic acid)∶V(water)=7∶3 mixed solvent

从图2可以看出,在搅拌速率为300 r·min-1,降温速率为0.1 K·min-1条件下得到的超溶解度曲线是一条几乎和溶解度曲线相互平行的两条曲线,且温度越高介稳区越窄。

4.2 动力学数据分析

结晶动力学研究过程中,结晶温度、降温速率、搅拌转速等外部因素通过悬浮密度、过饱和度、粒数密度等来影响晶体生长以及晶体颗粒品质。从养晶后开始降温起,取样分析来计算溶液的浓度、过饱和度以及过饱和比,即:

(5)

(6)

(7)

式中,mc、mw、mi分别为DNTF、水及乙酸的质量,g;Mc、Mw、Mi分别为DNTF、水及乙酸的相对分子质量,g·mol-1;C为溶液中DNTF的浓度,mol·mol-1;σ为相对过饱和度;S为过饱和比,Ceq为相同条件下与溶剂平衡的DNTF浓度,mol·mol-1。

粒度分析结果为各通道粒子的体积分率,各通道对应的晶体粒数密度可用下式计算[20]:

(8)

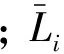
晶浆的悬浮密度采用重量法来确定,用取样器准确移取一定体积的晶浆,过滤后干燥,称取漏斗干燥前后质量m1、m2,即可得到悬浮密度:

MT=(m2-m1)/V

(9)

式中,m1,m2分别为漏斗质量和干燥后带有滤饼漏斗的质量,g;V为移取晶浆体积,mL。

4.3 动力学方程的回归

本研究忽略聚集、破碎对动力学数据的影响,实验中温度的变化范围为65～20 ℃,搅拌速度的范围为200～400 r·min-1。根据取样分析计算得到一系列不同实验条件的动力学数据,粒数密度分布图,即lnn与L的关系,如图3所示。溶液过饱和比S、悬浮密度MT以及由粒度分析结果按式(1)和(2)计算得到的成核速率BS和生长速率G值,结果列于表2。

从图3可以看出,粒数密度的对数值与粒度基本呈线性关系,说明晶体的生长呈线性无关规律。因此,按粒度无关模型研究来描述DNTF晶体的生长过程。

根据表2中DNTF的结晶动力学数据,即温度、溶液过饱和比S、悬浮密度MT、搅拌强度ωr以及成核速率BS和生长速率G,对照经验方程(1)和(2),通过多元线性最小二乘法回归动力学数据,得到结晶成核速率与生长速率方程中的各个动力学参数,即得到DNTF的结晶动力学方程如下:

(10)

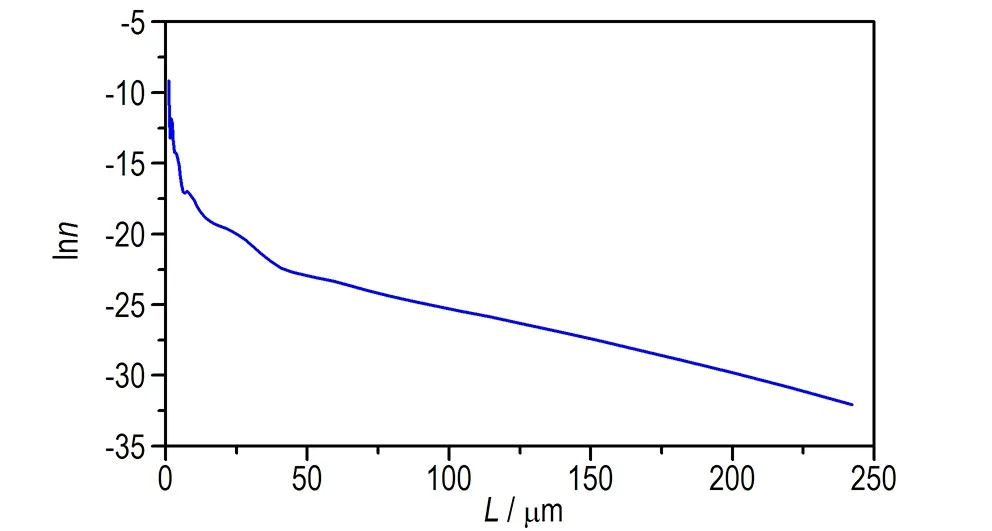
图3 DNTF的粒数密度与粒度关系

Fig.3 The relationship between population density and particle size of DNTF

表2 DNTF在V(乙酸)∶V(水)=7∶3的混合溶液中的结晶动力学数据计算结果

Table 2 Calculated results of the crystallization kinetics data of DNTF inV(acetic acid)∶V(water)=7∶3 mixed solvent

T/Ksupersatura⁃tionratiosuspensiondensity/g·mL-1stirringintensity/W·m-3growthrate/μm·s-1nucleationrate/mL-1·s-1327．151．240．02407．65 7．0750．000324．151．270．03412．94 11．6370．001318．151．320．04421．40 17．3920．003315．151．350．04424．24 1．9820．000306．151．440．05434．83 38．7230．007324．151．170．031904．84 10．2220．001318．151．200．041948．51 9．7670．001315．151．230．041974．62 5．1690．001309．151．210．052032．00 6．8560．002324．151．170．03977．64 19．8160．001321．151．190．04989．26 0．6670．001318．151．220．04998．34 0．2100．000315．151．250．041007．41 8．0050．003321．151．180．04417．21 10．8550．004312．151．250．05434．30 6．9920．003306．151．270．053444．57 2．0020．001327．151．140．03964．80 5．4840．001324．151．170．03977．47 1．2870．000321．151．190．04989．44 7．4140．002318．151．210．041002．23 1．5470．001312．151．260．051028．28 13．4050．004324．151．120．031898．63 9．2480．001321．151．130．041922．07 2．6370．000315．151．160．051967．94 7．0500．003312．151．170．051988．13 4．3650．002306．151．200．052028．27 15．8280．005

(11)

对结晶动力学方程分析可以发现,DNTF晶体的生长、成核速率相对于过饱和度的指数分别为3.83和1.3。这说明,增加系统的过饱和度能同时增加晶体的成核和生长速率,但生长速率增加更快。同时,晶体成核速率对于悬浮粒子密度的指数高达2.14,因此,随晶浆悬浮粒子密度的增大,晶体成核速率会显著上升而生长速率不变,这将不利于晶体的长大。

5 结 论

(1) 在间歇结晶器中,忽略聚集、破碎的影响,利用粒数衡算方程,对3,4-二硝基呋咱基氧化呋咱(DNTF)的冷却结晶动力学过程进行了研究,得到DNTF在V(乙酸)∶V(水)=7∶3的混合溶液中的冷却结晶动力学方程。

(2) 分析DNTF冷却结晶过程中晶体成核速率方程和生长速率方程,发现DNTF晶体的生长、成核速率相对于过饱和度的指数分别为3.83和1.3,说明增加系统的过饱和度能同时增加晶体的成核和生长速率,但生长速率增加更快; 晶体成核速率对于悬浮粒子密度的指数高达2.14,因此,随晶浆悬浮粒子密度的增大,晶体成核速率会显著上升而生长速率不变,这将不利于晶体的长大。该研究为DNTF冷却结晶特性的辨识、粒度分布的控制及工业放大提供了重要的理论指导。

参考文献:

[1] 周彦水, 李建康, 黄新萍, 等. 3,4-双(4′-氨基呋咱基-3′)氧化呋咱的合成及性能 [J]. 火炸药学报,2007, 30(1): 54-56.

ZHOU Yan-shui, LI Jian-kang, HUANG Xin-ping, et al. Synthesis, and properties of 3,4-bis (4′-furazanyl 3′) furoxan[J].ChineseJournalofExplosivesandPropellants, 2007, 30: 54-56.

[2] Sinditskii V P, Burzhava A V, Sheremetev A B, et al. Thermal and combustion properties of 3,4-bis(3-nitrofurazan-4-yl)furoxan (DNTF)[J].Propellants,Explosives,Pyrotechnics, 2012, 37(5): 575-580.

[3] 胡焕性, 张志忠, 赵凤起, 等. 高能量密度材料3,4-二硝基呋咱基氧化呋咱性能及应用研究 [J]. 兵工学报, 2004, 25(2): 155-158.

HU Huan-xing, ZHANG Zhi-zhong, ZHAO Feng-qi, et al. A study on the properties and application of high energy density material DNTF[J].ActaArmamentarii, 2004, 25(2): 155-158.

[4] 欧育湘, 刘进全. 高能量密度化合物[M]. 北京: 国防工业出版社, 2005: 14.

OU Yu-xiang, LIU Jin-quan. High Energy Density Compounds[M]. Beijing: National Defence Industry Press, 2005, 14.

[5] 陆杰, 王静康. 普鲁卡因青霉素结晶动力学[J]. 高校化学工程学报, 1999, 13(5): 403.

LU Jie, WANG Jing-kang. Crystallization kinetics of procaine benzylpenicillium[J].ChemicalEngineeringofChineseUnivisity, 1999, 13(5): 403.

[6] 王淑勤, 肖乐勤. 热重分析曲线影响因素的研究与探索 [J]. 河北化工, 2005, 28(4): 78-79.

Wang Shu-qin, XIAO Le-qin. Research and exploration on TGA curves influencing factors[J].HebeiChemicalEngineeringandIndustry, 2005, 28(4): 78-79.

[7] Jones A G, Mullin J W. Programmed cooling crystallization of potassium sulphate solutions[J].ChemicalEngineeringScience, 1974, 11(29): 105-118.

[8] Mersmann A, Angerhoefer M, Gutwald T, et al. General prediction of median crystal sizes[J].SeparationTechnology, 1992, 2(2): 85-97.

[9] Kazenin D A, Makeev A A, markov A V. Self-simulating growth of a spherical crystal in a binary solution[J].TheoreticalFoundationofChemicalEngineering, 1988, 21(6): 485-489.

[10] Simeone M, Palomba M, Volpicelli G. Size-dependent growth Rate of gypsum crystals by video-enhanced optical microscopy[C]∥Proceeding of 15th International Symposium on Industrial Crystallization, Italy, Separation, 15-18, 2002: 431-436.

[11] Tadayon A, Rohani S, Bennett M K. Nucleation and Growth Kinetics of (NH4)2SO4Using a Batch Cooling Crystallizer [C]∥Proceeding of 15th International Symposium on Industrial Crystallization. Italy, Separation, 15-18, 2002: 473-478.

[12] Tavare N S. Characterization of crystallization kinetics from batch experiment[J].SeparationandPurificationMethods, 1993, 22(2): 93-207.

[13] CUI Ke-jian, XU Zhi-bin, CHEN Li-ru, et al.Solubility of 3,4-bis(3-nitrofurazan-4-yl)furoxan in common solvents at temperatures between 293.15 K and 313.15 K[J].JChemEngData, 2013, 58(9): 2677-2680.

[14] LAN Guan-chao, WANG Jian-long, CHEB Li-zhen, et al. Measurement and correlation of the solubility of 3,4-bis(3-nitrofurazan-4-yl)furoxan (DNTF) in different solvents[J].JChemThermodyn, 2015, 89: 264-269.

[15] HOU Huan, WANG Jian-long, CHEN Li-zhen, et al. Experimental determination of solubility and metastable zone width of 3,4-bis(3-nitrofurazan-4-yl)furoxan (DNTF) in (acetic acid-water) systems from (298.15 K to 338.15 K)[J].FluidPhaseEquilibr,2016, 408(c): 123-131.

[16] Mullin J W. Crystallization[M]. London: Butterworths, 2000: 20-24.

[17] Randolph A D, LARSON M A. Theory of panic late process[M]. New York: Academic Press, 1971: 46.

[18] Myerson. Handbook of industrial crystallization[M]. London: Butter-heinemann, 2002: 130-131.

[19] Weijian Nong, Xiaopeng Chen, Linlin Wang, et al. Measurement and correlation of solubility of abietic acid in ethanol + water mixtures[J].JChemThermodyn, 2014, 68: 1990204.

[20] 王静康. 化学工程手册-结晶 [M]. 北京: 化学工业出版社, 2002: 9-13.

WANG Jing-kang. Handbook of chemical engineering-crystallization[M]. Beijing: Chemical Industry Press, 2002: 9-13.