基于橡胶弹簧非线性模型的重载车辆轮轨动力特征分析

张大伟，翟婉明，朱胜阳，王开云，刘鹏飞

(西南交通大学 牵引动力国家重点实验室，四川 成都 610031)

随着轨道交通技术和橡胶工业的快速发展，橡胶弹性元件在铁道车辆中的应用问题已得到较好解决，使得橡胶弹簧能够在有限的空间内实现良好的弹性，目前，橡胶弹簧在轨道交通车辆中得到了广泛应用。图1所示为几种典型的一系橡胶弹簧的结构形式，包括V形橡胶弹簧、锥形叠层橡胶弹簧以及承载鞍八字形橡胶垫等。其中，V形橡胶弹簧、锥形橡胶弹簧多用于地铁车辆一系悬挂系统中，我国研发的160 km/h快速货车转向架也采用了锥形叠层橡胶弹簧，该弹簧能提供垂向承载能力和较好的非线性刚度；而八字形轴箱橡胶弹簧主要应用于我国重载货车一系悬挂系统中，该弹簧可以有效减轻簧下质量，降低转向架与线路之间的不良动力。

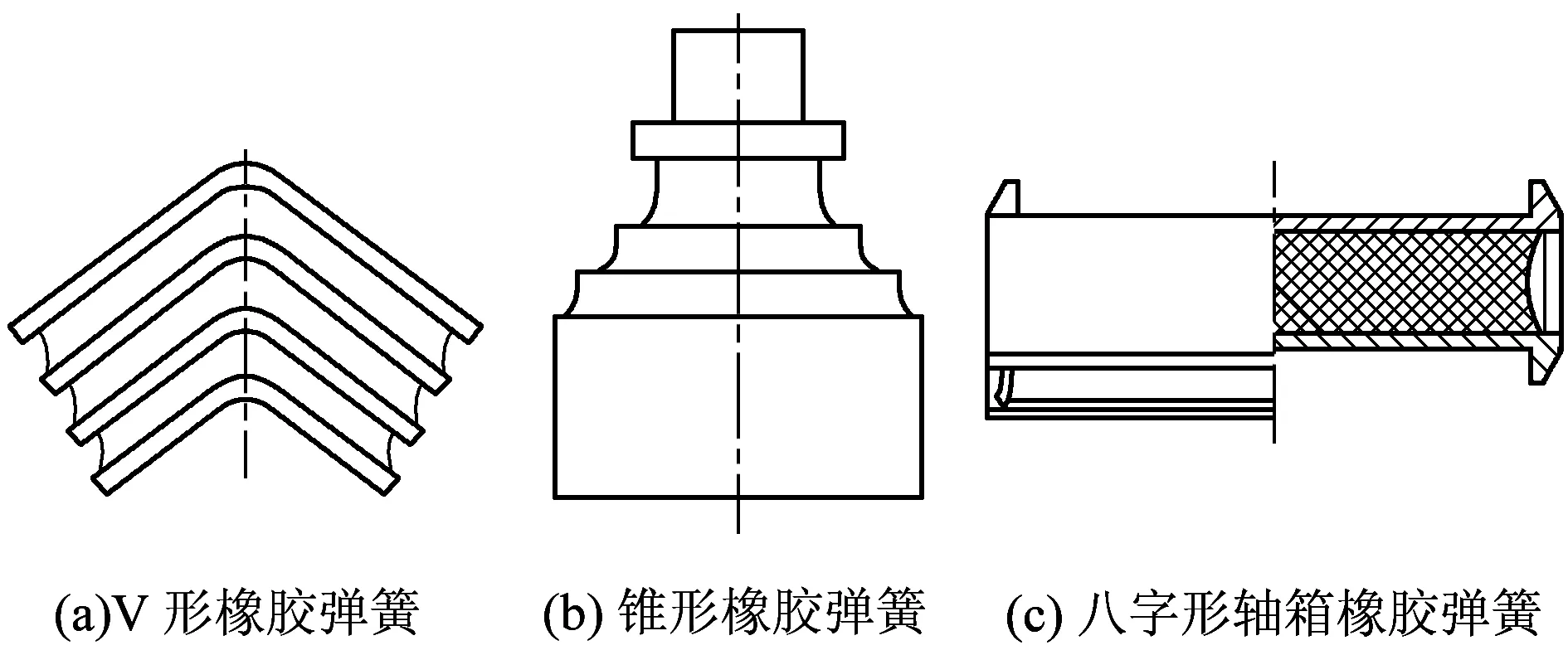
图1 铁道车辆中常用的橡胶弹簧

橡胶作为超弹性材料，其本构关系呈现出复杂的非线性。在地铁车辆[1]、高速列车[2]以及货车[3-4]悬挂系统橡胶元件的研究中，均发现橡胶弹性元件的弹性刚度有随激振频率不同而不断变化的现象，而传统的Kelvin-Voigt线性模型采用线性弹簧和阻尼并联的形式，文献[5]研究表明，该模型在反映激振频率与刚度特性的关系上存在一定的不足。铁道车辆在运行中往往会受到不同频率的激扰，尤其是对于重载铁路，由于轴重增加导致轮轨动力作用进一步加剧，准确描述橡胶元件刚度特性对研究重载车辆动态特性和重载车辆与轨道的耦合振动行为具有重要意义。因此，需要建立更为合理的橡胶弹性元件力学模型。

针对橡胶弹性元件的非线性物理模型，国内外众多学者展开了深入的研究。文献[6-7]对铁道车辆橡胶弹簧提出了一种与频率相关的非线性黏弹性力学模型，并与试验结果有良好的一致性。文献[5]将五参数的分数阶导数模型引入铁道车辆橡胶弹性元件的研究中，并且应用到单自由度振动系统中，分析指出分数阶导数模型在解决含橡胶元件振动系统的动力学问题中有更高的准确性。文献[8-9]将包含分数导数黏弹性单元、非线性摩擦单元的扣件胶垫非线性动力学模型引入到轮轨动力分析中，研究了高速铁路扣件胶垫的频率与幅值依赖性的非线性力学行为。文献[10]已证明介于0～2之间的任意阶导数均可表示阻尼，整数仅为分数的子集，分数阶可用于构建适用范围更广的阻尼模型。文献[11]提出了分数阶阻尼的三种形式，即分形导数、分数阶导数及正定分数阶导数，能准确描述黏弹性材料的记忆性和阻尼的分数次幂频率依赖。文献[12-14]利用分数阶导数模型表征汽车中橡胶弹性元件的力学特性，并应用到汽车振动问题的研究中，仿真结果和试验结果得到了较好的吻合。文献[15]详细介绍了铁道车辆结构中常用的橡胶弹性元件并进行了相关测试，指出橡胶元件普遍存在刚度非线性的力学特性。

橡胶弹性元件的力学行为研究已经取得了较多进展，而对于铁道车辆橡胶弹性元件的分数阶导数形式的黏弹性非线性模型的研究尚处于初始阶段。目前，橡胶弹簧的传统线性模型广泛应用于重载车辆-轨道耦合动力学系统中[16-17]。为了探讨橡胶元件力学非线性对轮轨动力作用的影响规律，本文针对重载车辆的一系悬挂橡胶弹簧，采用分数阶导数理论建立橡胶弹簧的非线性力学模型，将其嵌入重载车辆-轨道耦合动力系统中进行轮轨动力计算，并与采用传统线性模型的计算结果进行对比分析。

1 橡胶弹簧的非线性模型

橡胶弹性元件的传统线性模型如图2(a)所示，由线性弹簧和阻尼并联组成，而橡胶弹性元件的非线性模型则与之明显不同，其由线弹性恢复力、非线性摩擦力和采用分数阶导数形式的黏性力三部分组成，具体模型如图2(b)所示。因此，橡胶形变产生的作用力F即为弹性力Fe、橡胶材质内部摩擦产生的非线性摩擦力Ff、分数阶导数形式的黏性力Fa三者之和。

F=Fe+Ff+Fa

(1)

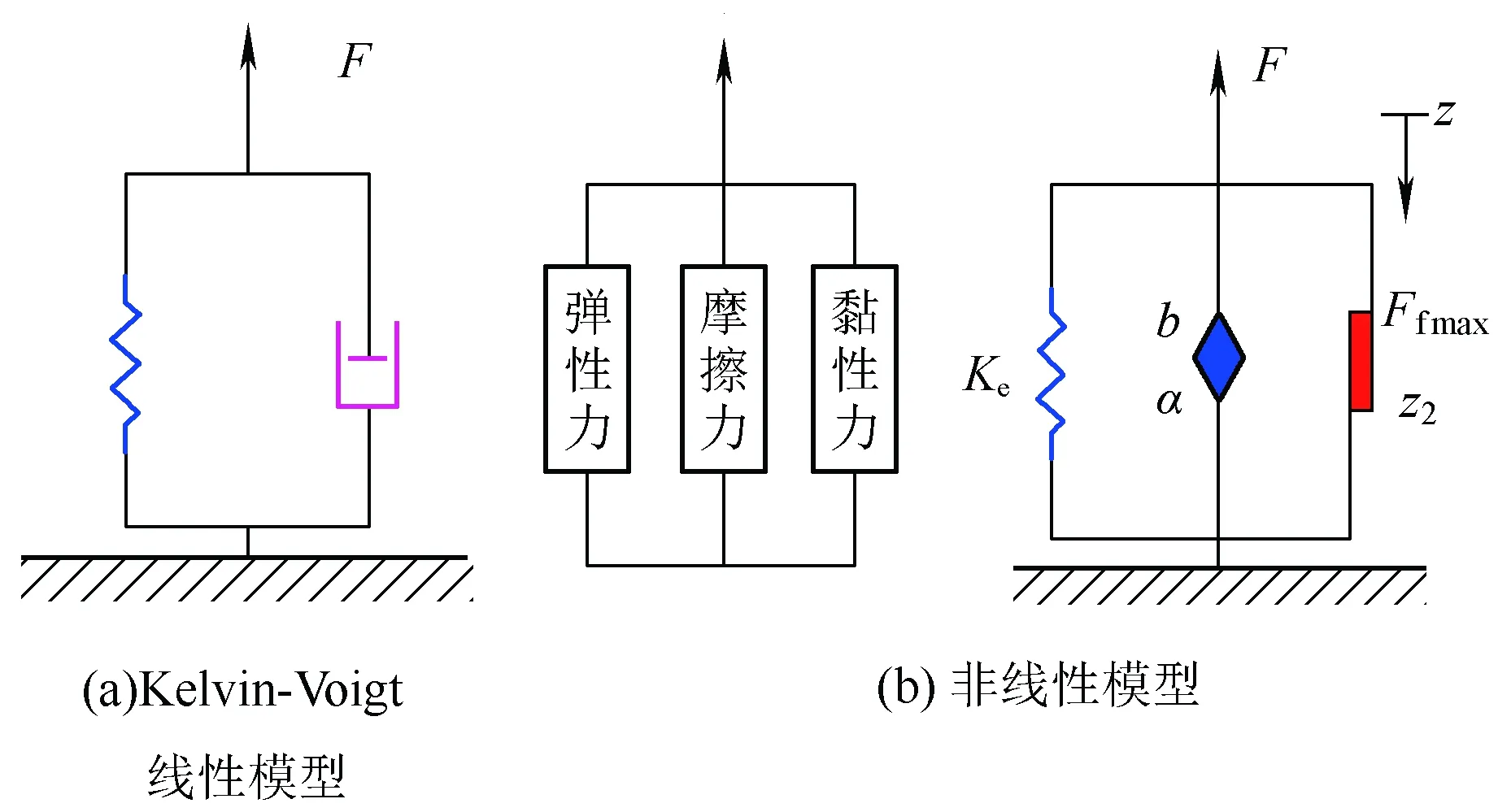
图2 橡胶弹性元件的线性和非线性模型

(1) 线弹性恢复力

弹性恢复力Fe为

Fe=Kez

(2)

式中：Ke为橡胶弹性元件弹性刚度；z为橡胶弹性元件的形变。

(2) 非线性摩擦力

摩擦力Ff可定义为[6-7]

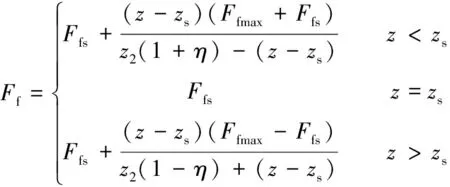
(3)

式中：Ffmax为最大摩擦力；z2为摩擦力方向变化产生的过渡位移，Ffmax、z2可由图3确定；η=Ffs/Ffmax，且η∈[-1,1]。(zs，Ffs)表示分支A、B的参考点，由该参考点利用式(3)可以计算当前时刻的摩擦力，计算过程中，由于摩擦力的方向不断发生变化，因此，需要实时更新参考点。

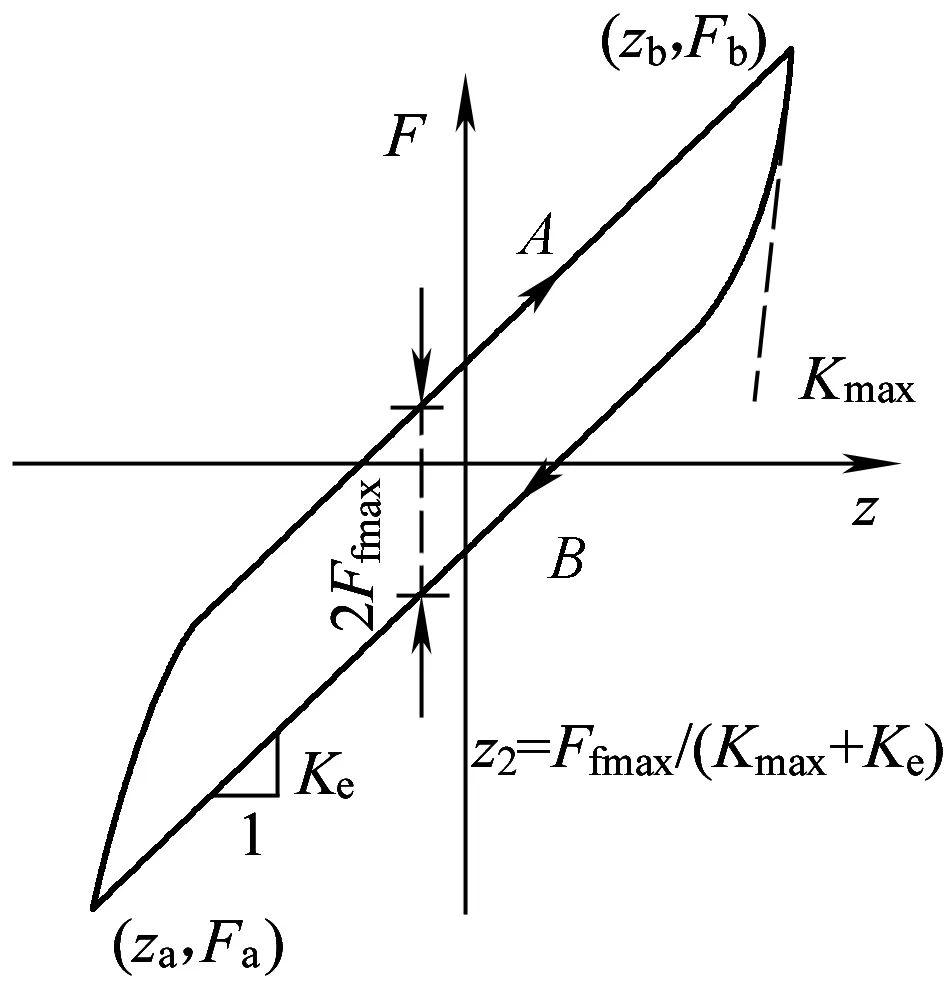
图3 橡胶元件典型的力-位移迟滞特性曲线

(3) 分数阶导数形式的黏性力

黏性力与位移的关系可以表示为[5]

Fa=bDαz

(4)

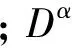
常见的Reimann-Liouville型分数阶微分[18]定义为

(5)

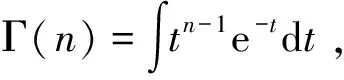
(6)

Grünwald-Letnikov进一步推广，得到数值计算的分数阶导数定义

(7)

对式(7)的离散表达式及截断误差进行分析，最终可得到

(8)

式中：Δt表示时间积分步长；下标n表示t=nΔt瞬时；zn表示tn瞬时弹性元件的形变；m∈[0,n-1]，表示第m个积分步长；z(n-m)表示t(n-mm)瞬时弹性元件的形变。式(8)即可应用到动力学问题的分析计算中，可以发现，tn时刻对应的作用力与之前所有时刻的位移均有一定关系，可体现出当前时刻作用力具有历史依赖性。

图3给出了由上述非线性模型得到的典型力-位移迟滞特性曲线。同时，由式(2)、式(3)和式(8)可知，在该非线性模型中，影响橡胶力-位移迟滞特性曲线的相关参数主要有Ke、Ffmax、z2、b、α等5个。为了得到该模型的参数，通常由两种情况下分别确定。首先，试验得到低频激励下的橡胶弹性元件的力-位移迟滞特性曲线，此时由于激振速度较低，相当于“静态”加载，黏性力较小，可忽略不计，由此可以确定Ke、Ffmax和z2三个参数(如图3所示)。然后，试验获得小位移中高频激励下的橡胶弹性元件的力-位移迟滞曲线，应用最小二乘法，确定b、α两个参数。表1为由某橡胶元件的力-位移迟滞特性曲线测试结果拟合得到的非线性模型参数的相关数值。

表1 某橡胶弹簧非线性模型参数

图4为橡胶弹性元件的非线性模型与测试结果的对比，由图4可知，在低频0.01 Hz和中频10 Hz正弦谐波激励下，两者力-位移迟滞特性曲线吻合较好，表明非线性模型能够较好地表征橡胶弹簧的力学特性。

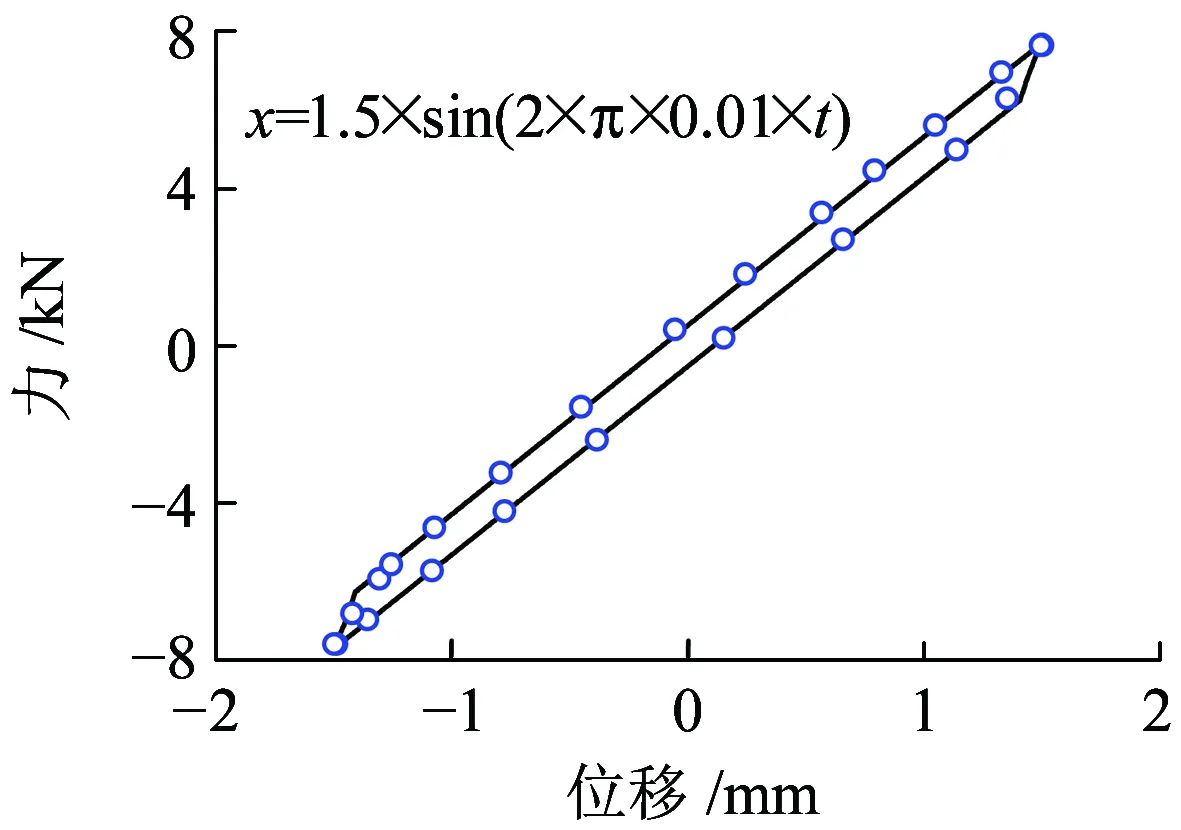
(a)0.01 Hz，激励位移1.5 mm

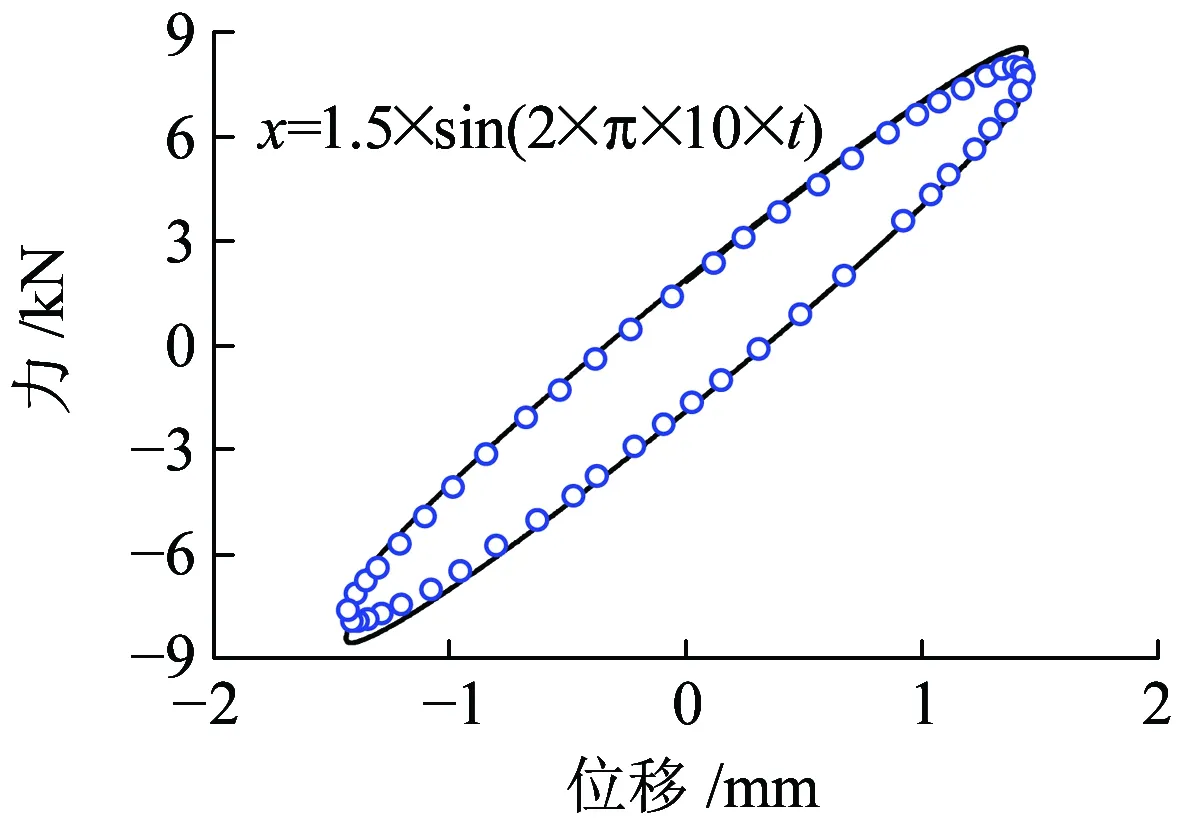
(b)10 Hz，激励幅值1.5 mm图4 橡胶弹簧的非线性模型与测试结果对比

2 考虑橡胶弹簧力学非线性的车辆-轨道垂向耦合模型

由前述可知，橡胶弹性元件已普遍应用于铁道车辆一系悬挂系统中，因此，有必要利用非线性模型对一系橡胶弹性元件建模以分析其动力学特性。现以国内安装有八字形轴箱橡胶弹簧的某型25 t轴重重载车辆为例，建立考虑橡胶力学非线性的重载车辆-轨道垂向耦合模型。

图5为本文采用的以轮轨接触关系为“纽带”的车辆-轨道耦合动力学模型[16-17]。其中，重载车辆采用传统的“三大件”式转向架，轮对和侧架之间的一系悬挂为八字形轴箱橡胶弹簧，车体(摇枕)和侧架之间的二系悬挂由圆弹簧和楔块组成。根据重载车辆的具体结构形式，车辆子系统可建立为包含有10个自由度的多刚体系统，具体地，车体和侧架考虑沉浮和点头运动，而轮对只考虑其沉浮运动。对于悬挂系统，一系悬挂采用上述橡胶元件非线性模型，而二系悬挂采用线性弹簧和摩擦副并联的物理模型。同时，考虑到重载轨道结构形式为75 kg/m钢轨、Ⅲ型混凝土轨枕和碎石道床，因此轨道子系统可采用三层点支承的梁模型，其中，钢轨可视为有限长的Bernoulli-Euler梁模型，混凝土轨枕和道床块视为刚体，只考虑其垂向振动。最后，车辆子系统和轨道子系统可利用Hertz非线性弹性接触模型耦合在一起。

图5 重载车辆-轨道耦合动力学模型

根据达朗贝尔原理，同时考虑橡胶弹性弹簧的非线性模型，轮对沉浮的运动方程为

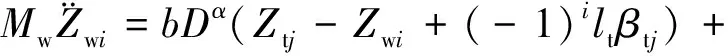
(9)

侧架的沉浮运动方程为

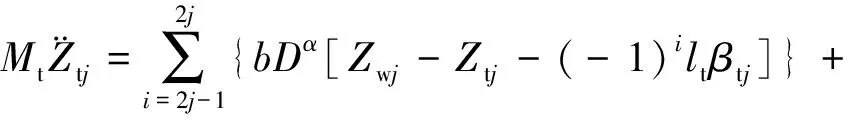
(10)

侧架的点头运动方程为

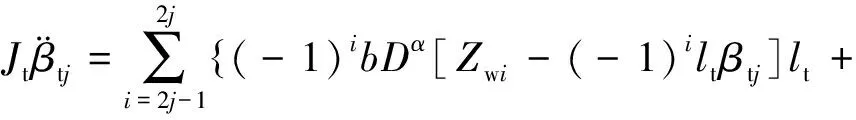
(11)

车体的沉浮运动方程为

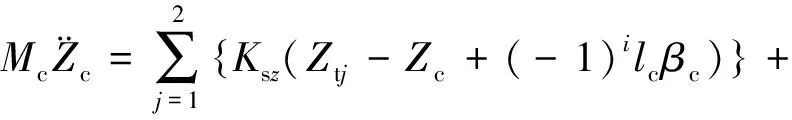
(12)

车体的点头运动方程为

(13)

式中：Zwi、Ztj、βtj、Zc、βc分别表示轮对沉浮、侧架沉浮和点头以及车体沉浮和点头运动；Mc、Mt和Mw分别表示车体(含摇枕)质量、侧架(两个)质量和轮对质量；Jc和Jt分别表示车体和侧架的点头惯量；Ksz和Fszj分别表示二系悬挂的刚度和摩擦力；Pi表示轮轨垂向力；lc为车辆定距之半；lt为转向架轴距之半；i为车辆轮对的顺序编号，i=1～4；j为侧架的顺序编号，当i=1，2时，j=1；当i=3，4时，j=2。

为了求解二系悬挂的摩擦力Fszj，分析货车二系悬挂摩擦减振器非线性作用模型[16]，如图6所示。其包括两部分，分别为弹簧支撑和楔块式摩擦减震器。由于与车辆重量相比，楔块质量非常小，因此，可以忽略楔块的惯性力。图6给出了减震器楔块受力情况，Nj为楔块弹簧的反力；Sj、Fj为楔块两摩擦面间的正压力;α1为斜楔摩擦角。若主副摩擦面的摩擦系数相同，均取为μs，其摩擦力可以取以下的简单形式进行计算。

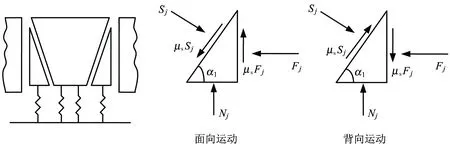
图6 二系悬挂摩擦减振器非线性作用模型

楔块弹簧的反力为

Nj=Ksz1[Zc+(-1)jlcβc-Ztj]

(14)

式中：Ksz1为支撑斜楔的弹簧刚度。

忽略楔块的惯性力后，由受力平衡可以得到

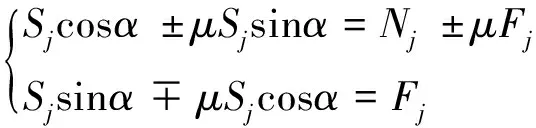
(15)

简化得到

(16)

因此，二系悬挂摩擦力为

Fszj=2Nj±2μFj

(17)

式(14)～式(17)中，j=1～2。当摇枕和侧架面向运动时，±和∓取上面的符号；当摇枕和侧架背向运动时，±和∓取下面的符号。

重载车辆的相关参数详见表2，表中，R表示滚动圆半径；v表示行车速度。轨道子系统的振动方程参见文献[16-17]，在此不再赘述，表3给出了轨道结构的具体参数。

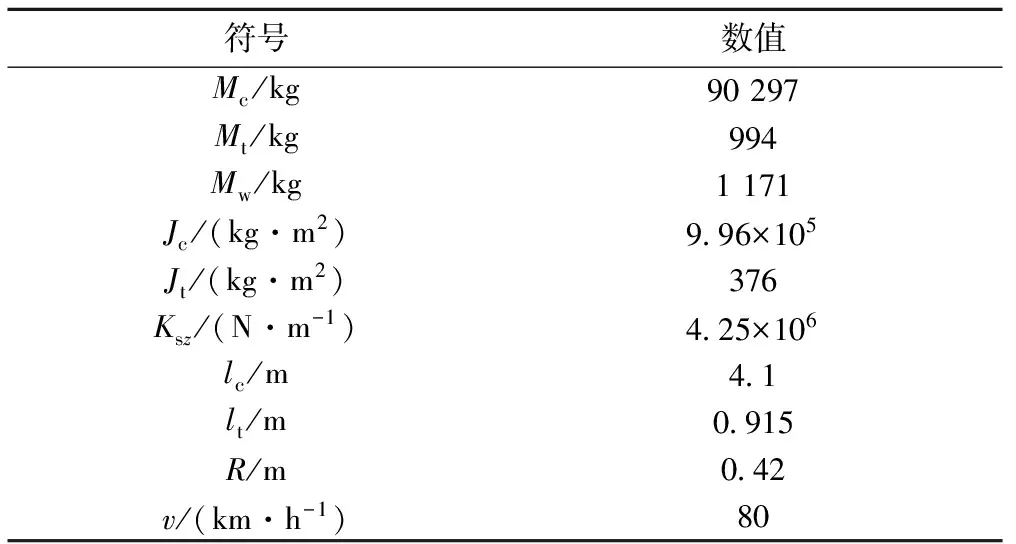
表2 重载车辆垂向模型参数

表3 重载轨道结构参数

为了探讨橡胶弹簧非线性对轮轨动力特性的影响，以表4给出的重载车辆轴箱橡胶弹簧非线性模型参数为例进行分析。需要指出的是，由于橡胶元件生产制造及使用状态等条件的差异，上述橡胶元件的非线性模型参数可能会有所不同。图7(a)为一系悬挂橡胶元件采用上述非线性模型参数构建时，在连续谐波激扰下重载车辆-轨道系统中橡胶元件动载荷-位移的变化特性。图中给出了相同谐波幅值条件下，频率分别为40 Hz、50 Hz和60 Hz时的动荷载-位移迟滞特性曲线，可见，三种激励频率对应的载荷-位移迟滞特性曲线明显不同。迟滞曲线包络的面积即一次循环加载卸载过程中损耗的能量，比较三种频率下的包络面积可知，40 Hz频率下的包络面积明显比50 Hz和60 Hz频率下的包络面积要小很多。由此可知，激振频率越高，橡胶弹簧能量消耗越大，阻尼效应也越明显。

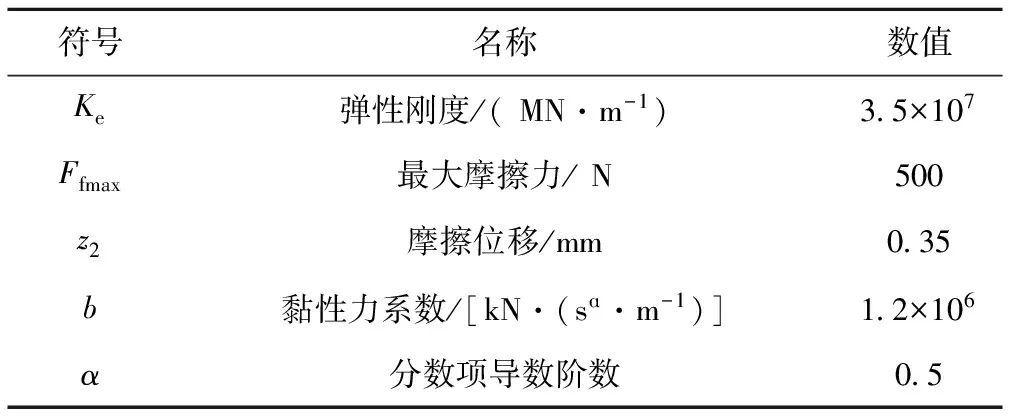
表4 轴箱橡胶弹簧非线性模型参数

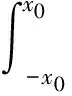
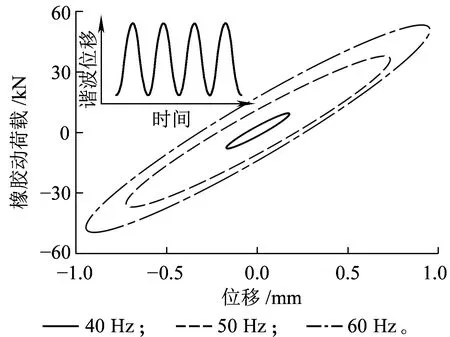
(a)典型迟滞曲线

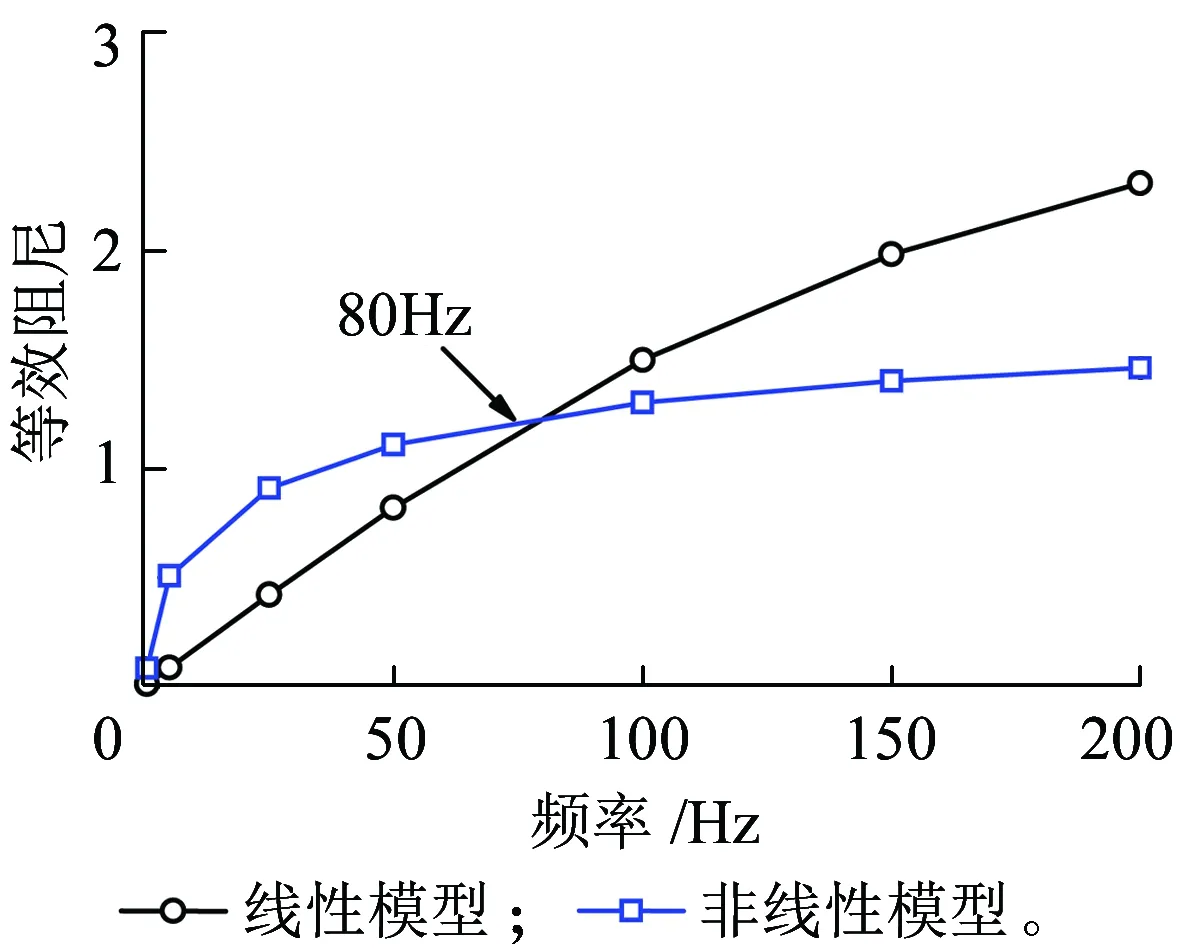
(b)不同频率下的刚度和阻尼特性图7 不同频率下的橡胶弹簧动态特性

3 橡胶弹簧非线性特性下的轮轨动力特征

为了研究考虑橡胶弹簧非线性特性条件下的轮轨动力特征，应用上述建立的重载车辆-轨道垂向耦合动力学模型，计算车轮扁疤冲击和轨道随机不平顺激扰下的车辆与轨道动态响应，并与考虑橡胶弹簧线性特性条件下的轮轨动态特征进行比较分析。

3.1 车轮扁疤冲击轮轨动力作用分析

冲击荷载选取为重载车辆中常见的车轮擦伤引起的扁疤冲击，如图8所示。同时，利用翟方法[19]对基于橡胶弹簧线性模型和非线性模型的车辆-轨道耦合动力系统分别进行求解，并比较两种模型条件下轮轨动态响应的不同。

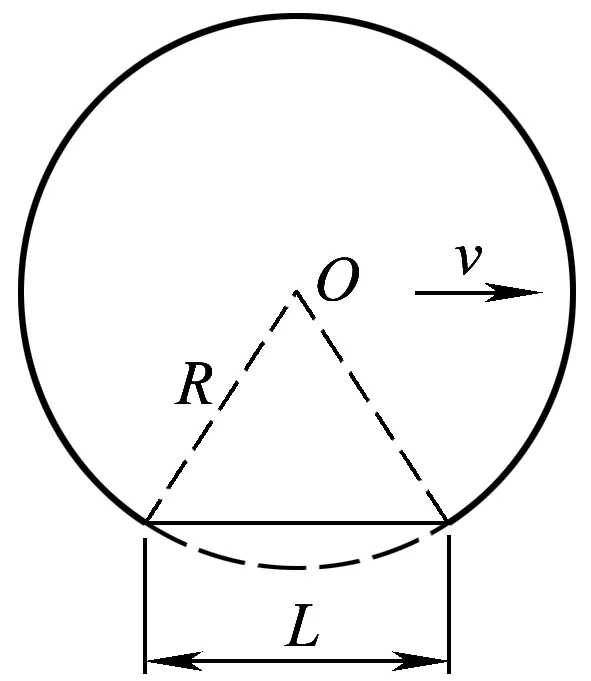
图8 车轮扁疤模型

翟积分算法可以表示为

(18)

(19)

由车轮扁疤引起的冲击速度[17]为

(20)

(21)

式中：L为车轮扁疤长度，L=50 mm；γ为车轮旋转惯量转换的往复惯量系数。

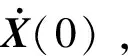
(2)由式(18)计算tn时刻的位移Xn。

(3)从Xn中取出Zwi、Ztj、βtj积分结果，由式(2)计算橡胶元件的弹性恢复力Fe，由式(8)计算橡胶元件的黏性力，由式(3)计算橡胶元件的摩擦力Ff；从Xn中取出Ztj、Zc，βtj积分结果，计算二系悬挂的线弹性力、阻尼力及摩擦力。

(4)由(3)可得到式(9)～式(13)等号右边外力的合力矩阵Fn。

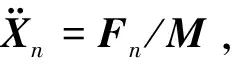
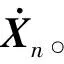
(7)由式(18)计算tn+1时刻的位移Xn+1。

(8)重复(3)～(7)，并判断当tn=t1时，令1位轮对的沉浮振动速度Zw1=v0，仿真t1时刻车轮扁疤冲击响应。

车轮扁疤激扰下轮轨垂向力计算结果如图9所示。由图9(a)可知，非线性模型和线性模型下的轮轨垂向力振动响应有所不同，但总体差异不大。两种模型下轮轨垂向力P1无明显差别，均为378.2 kN，而P2略有不同，非线性模型中轮轨力P2为202.6 kN，线性模型中轮轨力P2为209.8 kN，前者比后者略小，相差不大。文献[20]研究也表明，在冲击荷载条件下，一系悬挂(即橡胶弹簧)刚度和阻尼变化时，轮轨垂向力P1和P2变化并不明显，这也就是线性模型和非线性模型相差不大的原因所在。

图9(b)给出了频域内轮轨垂向力的变化情况。可以看到，两种模型中轮轨垂向力的不同之处主要表现在200 Hz以下的中低频区域。当频率在10～80 Hz范围内时，非线性模型的轮轨垂向力谱密度值比传统线性模型下的轮轨垂向力谱密度值略大，由图7(b)可知，其原因为在80 Hz以下频率范围内，线性模型的阻尼要比非线性模型要小，这表明传统模型会低估10～80 Hz频率范围内的轮轨垂向力，而在80～200 Hz频率范围内，非线性模型中的轮轨垂向力谱密度值比传统模型下的轮轨垂向力谱密度值要小，由图7(b)可知，其原因为在80Hz以上频率范围内，线性模型的阻尼要比非线性模型要大，表明传统模型可能高估了该频率范围内轮轨垂向力。

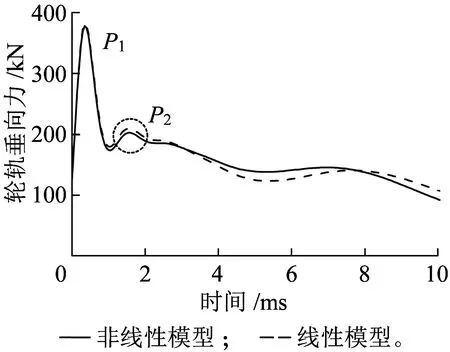
(a)轮轨垂向力振动响应

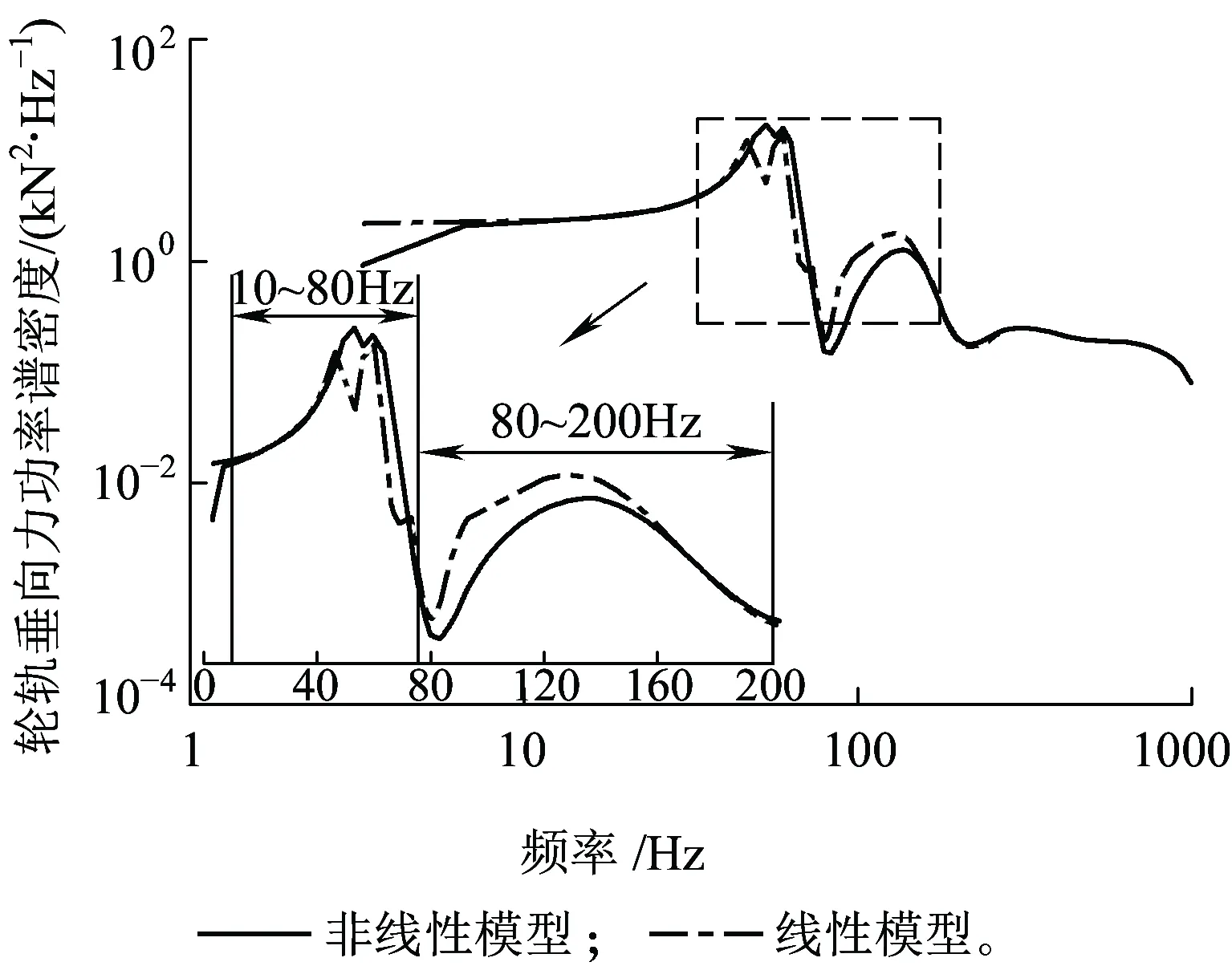
(b)功率谱密度曲线图9 轮轨垂向力振动响应时程图和功率谱密度曲线

3.2 轨道随机不平顺下的轮轨动力作用分析

为比较轨道随机不平顺作用下的轮轨动力响应，选取某重载铁路实测轨道不平顺(如图10所示)作为激扰输入车辆-轨道垂向耦合动态系统中，并对比橡胶弹簧的非线性模型和线性模型对轮轨垂向力以及车辆结构振动加速度等指标影响的差异。

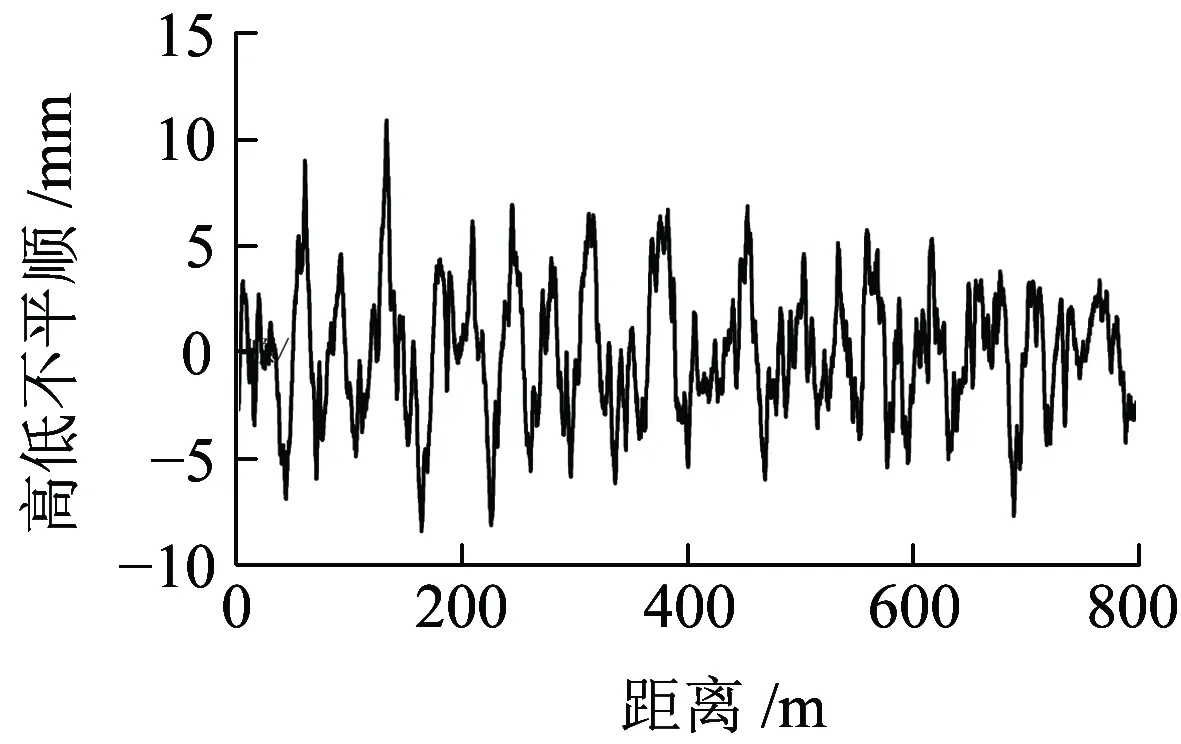
图10 实测轨道随机不平顺

图11为随机不平顺作用下轮轨垂向力的动态响应时程图，从图11(a)可知，橡胶元件的两种力学模型对应的轮轨垂向力有所不同。非线性模型中轮轨垂向力的最大值和最小值分别为184.5 kN和45.0 kN，而线性模型对应的轮轨垂向力的最大值和最小值则分别为173.2 kN和62.4 kN，最大值前者比后者有所增大，而最小值前者比后者略有减小，可见两种模型下的轮轨垂向力有明显的不同，尤其是最小轮轨垂向力。图11(b)为轮轨垂向力概率密度分布曲线，可见两种模型下轮轨垂向力的分布差异同样明显，非线性模型中轮轨垂向力在静轮重120 kN附近的概率密度要比传统线性模型对应的概率密度要低，而在轮轨垂向力较低区域和较高区域，前者要比后者概率密度要高。

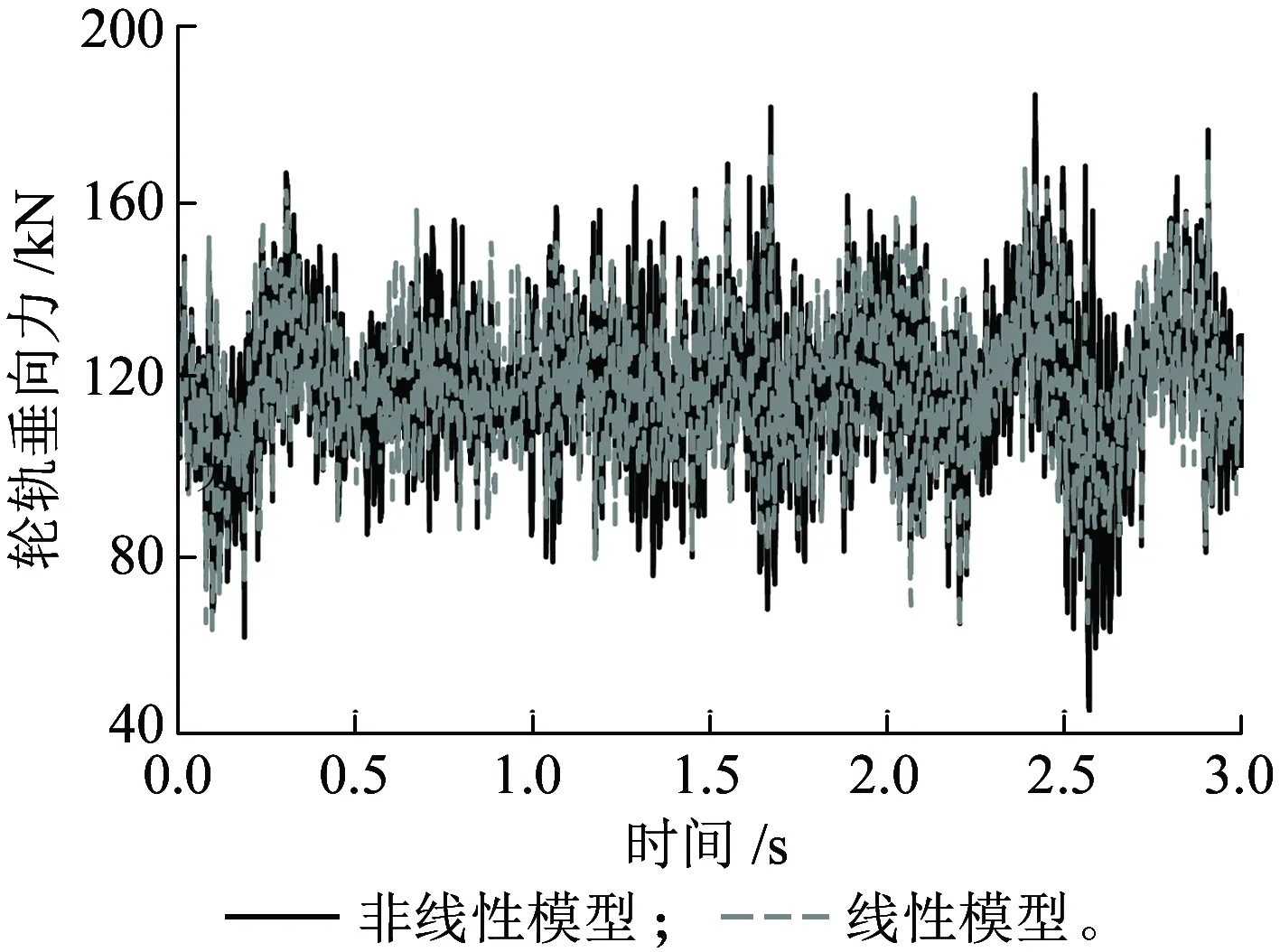
(a)轮轨垂向力振动响应

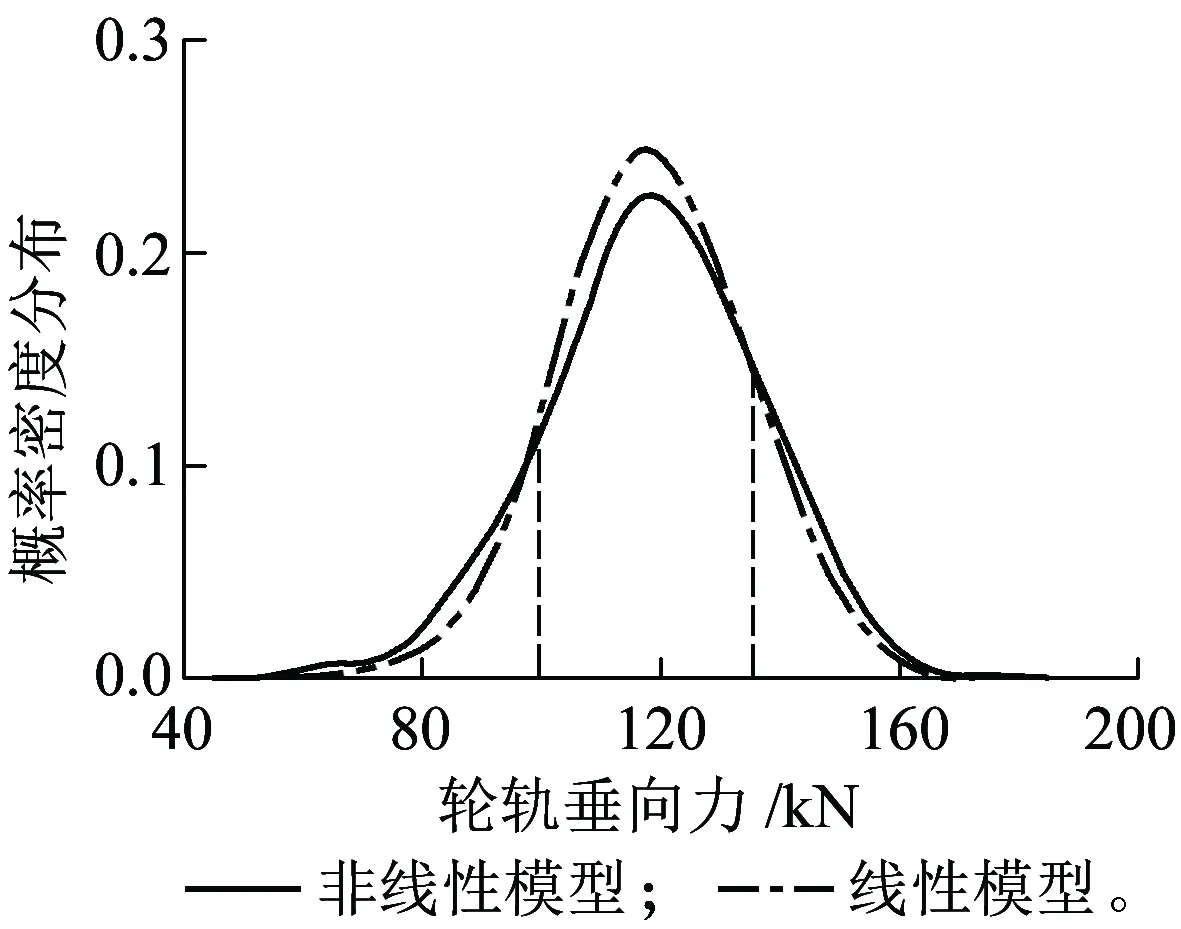
(b)概率密度分布曲线图11 轮轨垂向力振动响应时程图和概率密度分布曲线

图12为两种模型下轮轨垂向力的功率谱密度曲线对比，可以看出，图中存在两个主频区，第一个为2 Hz左右的低频，主要为车体振动引起的，第二个为50 Hz左右的中频，反应了车轮与轨道共同变形的耦合振动。从这两个主频区可以发现，非线性模型对应的谱密度值均比传统线性模型稍大，与冲击荷载作用下的结论一致，也解释了非线性模型中轮轨垂向力最大值要比线性模型稍大的原因。

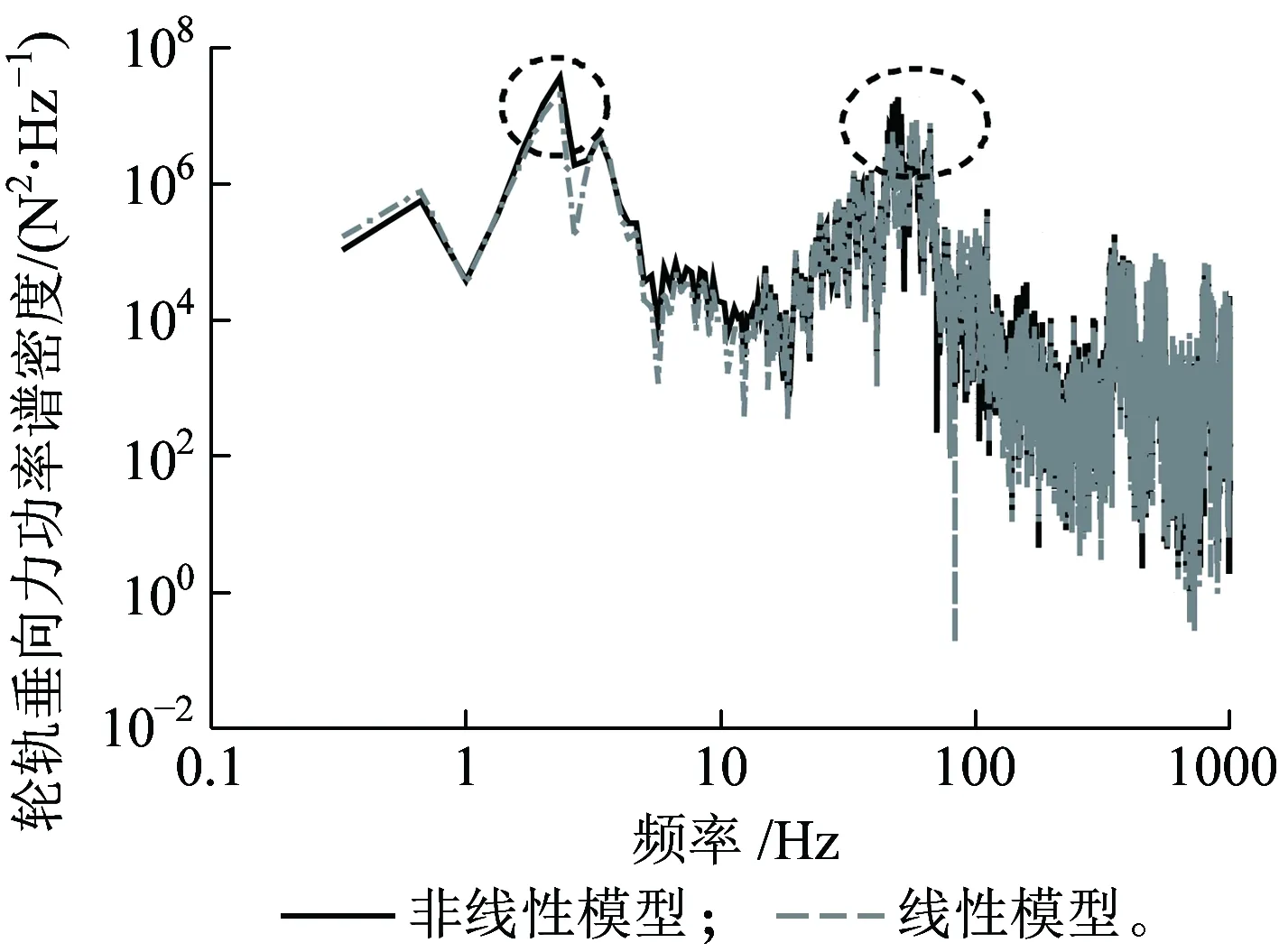
图12 轮轨垂向力功率谱密度

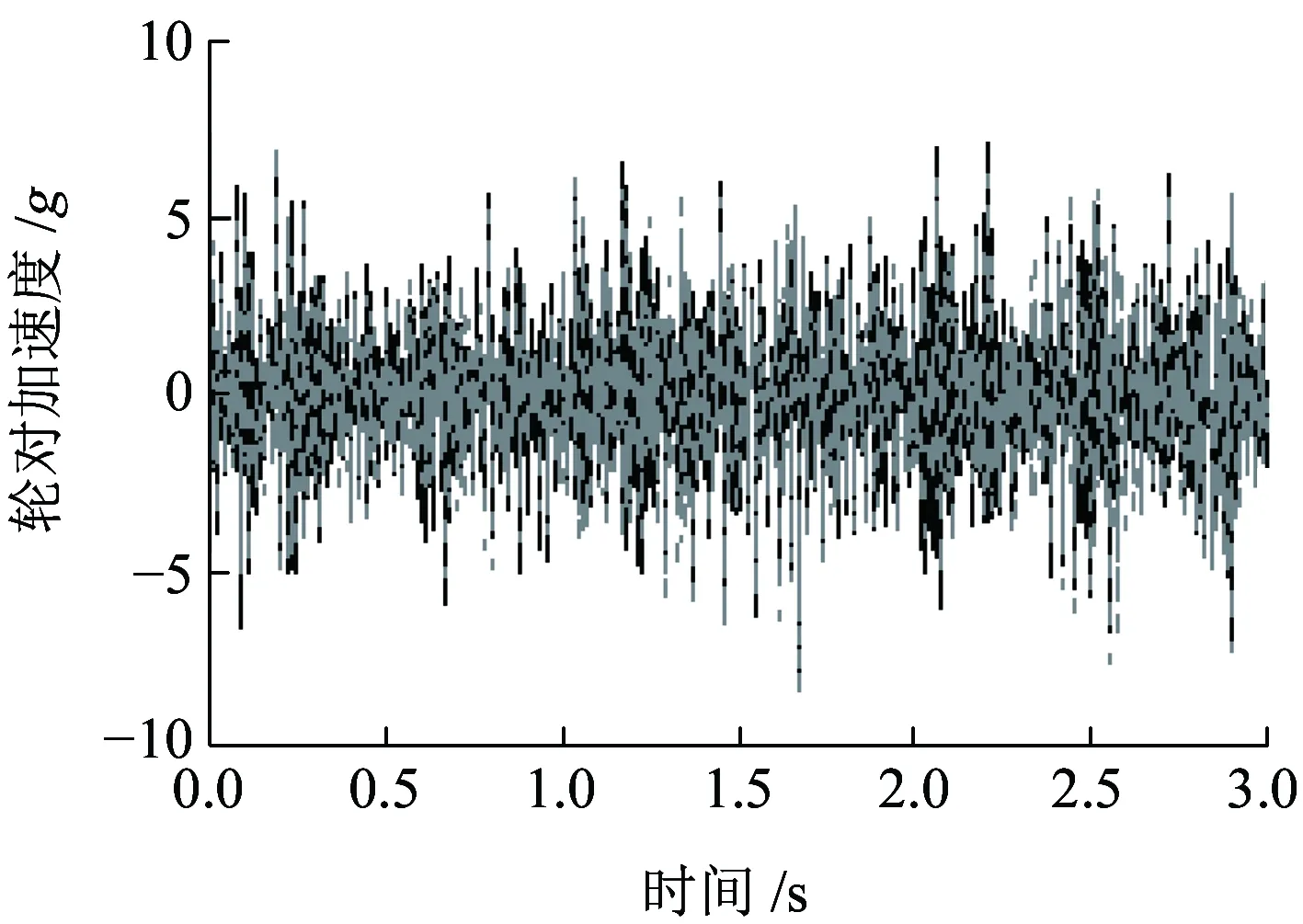
(a)轮对

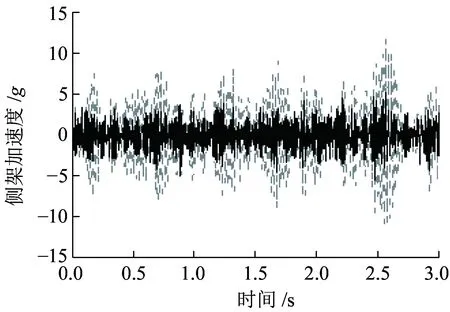
(b)侧架

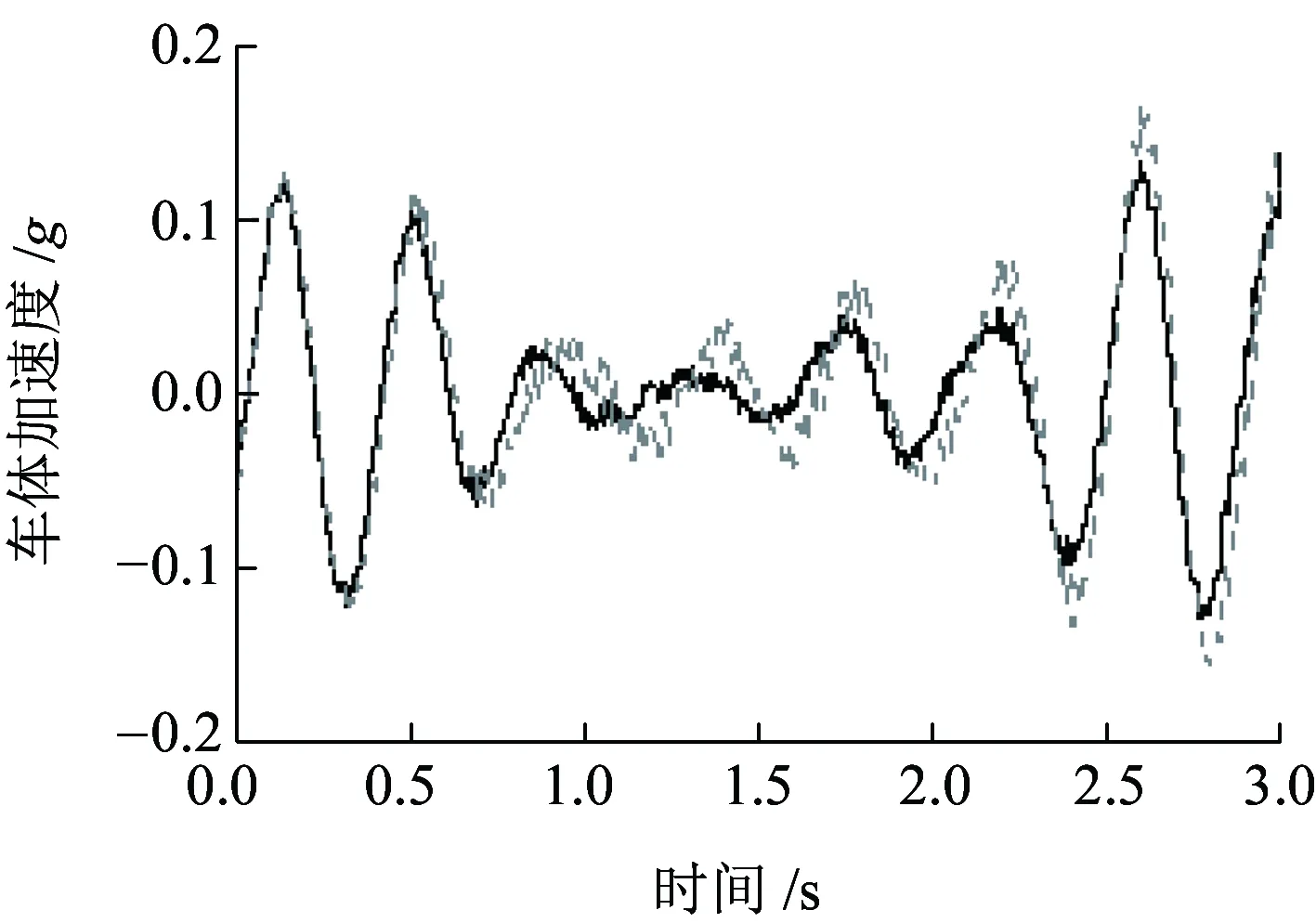
(c)车体

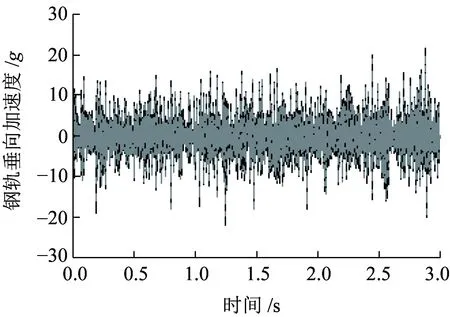
(d)钢轨图13 车辆结构和钢轨加速度时程图

图13为车辆结构与钢轨振动加速度时程曲线。图13(a)和图13(d)分别为轮对加速度和钢轨加速度振动响应时程图，可见两种模型对应的轮对垂向加速度均在7.2g左右，钢轨垂向加速度均在20g左右，即该两种指标未发生明显的变化。然而侧架垂向加速度和车体垂向加速度却有明显的不同，如图13(b)和图13(c)所示。对于侧架垂向加速度，非线性模型和线性模型对应的最大值分别为5.8g和12.0g，前者比后者降低了约一半，变化比较明显；对于车体垂向加速度，非线性模型和线性模型对应的最大值分别为0.13g和0.17g，前者比后者降低了0.04g，变化较小。可见，非线性模型下，轮对加速度同传统模型差异不大，而侧架加速度和车体加速度却比传统模型小很多。

由图12的轮轨垂向力功率谱密度曲线可知，轮轨垂向力主要频率集中在80 Hz以下，从图7(b)可知，此时对应的非线性模型的阻尼效应大于线性模型。因此从系统振动指标来看，线性模型对应的轮轨垂向力较非线性模型对应的轮轨垂向力略小。而对于侧架和车体的振动，由于两者位于一系橡胶悬挂的上部，振动向上传递到两者时，已经经过橡胶弹簧的隔振作用，由上述分析可知非线性模型对应的等效阻尼比线性模型的阻尼要大，也就是说能量吸收效果更明显，振动衰减作用更明显，因此橡胶弹簧非线性模型下仿真得到的侧架和车体振动加速度要比线性模型小。

4 结论

本文针对轨道交通常见的橡胶弹性弹簧建立了采用分数阶导数理论的非线性模型，探讨了该非线性模型在重载车辆-轨道耦合动态系统中的应用，并比较了非线性模型同传统线性模型在轮轨动力响应计算中的差异。得到如下结论：

(1)由线弹性恢复力、非线性摩擦力和采用分数阶导数形式的黏性力三部分组成的橡胶弹簧非线性模型可以较好地表征橡胶弹簧的力学特性。

(2)在重载车辆-轨道耦合系统模型中，一系悬挂橡胶弹簧分别用线性模型和非线性模型构建时，采用前者会低估10～80 Hz频率范围内的轮轨垂向力，且高估了80～200 Hz频率范围内的轮轨垂向力。

(3)在轨道随机不平顺条件下，橡胶弹簧非线性模型和线性模型中轮轨垂向力的概率密度分布差异明显，非线性模型中轮轨垂向力最大值略有增加，而最小值略有下降。同时，非线性模型计算得到的轮对垂向加速度和钢轨垂向加速度幅值与线性模型差异不大，而侧架垂向加速度和车体垂向加速度比线性模型均有所降低。

综上所述，橡胶弹性元件的历史依赖特性对车辆-轨道耦合动态系统有明显的影响，利用分数阶导数理论构建橡胶元件非线性力学模型在车辆与轨道动态相互作用分析中可以得到有效地应用。

参考文献：

[1]孟政. 橡胶弹簧频变刚度特性及其对地铁车辆动力学性能的影响研究[D]. 成都：西南交通大学, 2011.

[2]何灼馀. 高速动车组转向架一系橡胶节点频率-刚度特性及其影响研究[D]. 成都：西南交通大学, 2012.

[3]张丽霞. 快速货车橡胶减振元件静、动态特性分析[D]. 成都：西南交通大学, 2013.

[4]张春良. 转K7型铁路货车转向架橡胶弹性元件研制[D]. 成都：西南交通大学, 2012.

[5]SJÖBERG M M, KARI L. Non-linear Behavior of a Rubber Isolator System Using Fractional Derivatives[J]. Vehicle System Dynamics, 2002, 37(3): 217-236.

[6]BERG M. A Model for Rubber Springs in the Dynamic Analysis of Rail Vehicles[J]. Proceedings of the Institution of Mechanical Engineers, Part F: Journal of Rail and Rapid Transit, 1997, 211(2): 95-108.

[7]BERG M. A Non-linear Rubber Spring Model for Rail Vehicle Dynamics Analysis[J]. Vehicle System Dynamics, 1998, 30(3-4): 197-212.

[8]ZHU S Y, CAI C B, SPANOSPOL D. A Nonlinear and Fractional Derivative Viscoelastic Model for Rail Pads in the Dynamic Analysis of Coupled Vehicle-slab Track Systems[J]. Journal of Sound and Vibration, 2015,335: 304-320.

[9]ZHU S Y, CAI C B, LUO Z, et al. A Frequency and Amplitude Dependent Model of Rail Pads for the Dynamic Analysis of Train-track Interaction[J]. Science China Technological Sciences, 2015, 58(2): 191-201.

[10]王在华, 胡海岩. 含分数阶导数阻尼的线性振动系统的稳定性[J]. 中国科学: G 辑, 2009(10): 1 495-1 502.

WANG Zaihua, HU Haiyan. Stability of A Linear Oscillator with Damping Force of Fractional-order Derivative[J]. Science in China:Series G, 2009, 39(10): 1 495-1 502.

[11]张晓棣, 陈文. 三种分形和分数阶导数阻尼振动模型的比较研究[J]. 固体力学学报, 2009, 30(5): 496-503.

ZHANG Xiaodi, CHEN Wen. Comparison of Three Fractal and Fractional Derivative Damped Oscillation Models[J]. Chinese Journal of Solid Mechanics, 2009, 30(5): 496-503.

[12]吴杰, 上官文斌. 采用黏弹性分数导数模型的橡胶隔振器动态特性的建模及应用[J]. 工程力学, 2008, 25(1): 161-166.

WU Jie, SHANGGUAN Wenbin. Modeling and Applications of Dynamic Characteristics for Rubber Isolators Using Viscoelastic Fractional Derivative Model[J]. Engineering Mechanics, 2008, 25(1): 161-166.

[13]潘孝勇, 上官文斌, 柴国钟, 等. 基于超弹性、分数导数和摩擦模型的碳黑填充橡胶隔振器动态建模[J]. 振动与冲击, 2007, 26(10): 6-10.

PAN Xiaoyong, SHANGGUAN Wenbin, CHAI Guo-zhong, et al.Dynamic Modeling for Carbon-Filled Rubber Isolators Based on Hyper-Elasticity, Fractional Derivative and a Generalized Frictional Model[J]. Journal of Vibration and Shock, 2007, 26(10): 6-10.

[14]潘孝勇, 柴国钟, 上官文斌. 含有橡胶隔振器振动系统时域响应的测试与计算分析[J]. 振动与冲击, 2007, 26(12): 32-35.

PAN Xiaoyong, CHAI Guozhong, SHANGGUAN Wenbin. Experiment and Calculation on the Time Response of a System Including Rubber Isolator[J]. Journal of Vibration and Shock, 2007, 26(12): 32-35.

[15]刘建勋, 卜继玲. 轨道车辆转向架橡胶弹性元件应用技术[M]. 北京：中国铁道出版社, 2012.

[16]翟婉明. 车辆-轨道耦合动力学[M]. 4版. 北京：科学出版社, 2015.

[17]ZHAI W M, WANG K Y, CAI C B. Fundamentals of Vehicle-track Coupled Dynamics[J]. Vehicle System Dynamics, 2009, 47(11): 1 349-1 376.

[18]陈文,孙洪广, 李西成, 等. 力学与工程问题的分数阶导数建模[M]. 北京：科学出版社, 2010.

[19]ZHAI W M. Two Simple Fast Integration Methods for Large-scale Dynamic Problems in Engineering[J]. International Journal for Numerical Methods in Engineering, 1996, 39(24): 4 199-4 214.

[20]杨春雷, 李芾, 黄运华. 一系垂向悬挂对重载货车轮轨动力作用的影响[J]. 西南交通大学学报, 2011, 46(5): 820-825.

YANG Chunlei, LI Fu, HUANG Yunhua. Optimization of Primary Vertical Suspension of Heavy Haul Freight Car[J]. Journal of Southwest Jiaotong University, 2011, 46(5): 820-825.