基于传播图理论的隧道场景无线信道模型构建与验证

张嘉驰，陶 成，孙溶辰，谈振辉，刘 留

(北京交通大学 宽带无线移动通信研究所，北京 100044)

我国城市地下轨道交通蓬勃发展，且具有快速、便捷、大运量的特点。北上广深和几乎所有的省会城市都已经建设了轨道交通或者正在进行轨道交通建设规划。广州计划2020年轨道交通里程达到500 km[1]。随着城市轨道交通信息化的发展，系统要求的车地之间的通信数据越来越多。一方面，列车运行、安全监控、维护等实时信息需要传送至地面，以满足铁路路网对移动体实时动态跟踪和信息传输的需要；另一方面，以旅客为主体的移动数据信息也需要在车地之间实时传送[2]。因此，为了保证地下轨道交通的顺畅运营，对其无线信道的特性研究尤为重要，否则将会制约地下轨道交通的全面发展。

隧道环境是地下轨道交通的主体。目前，已经有多种理论方法研究电磁波在隧道中的传播特性，如射线理论[3]和模态理论[4]。在此理论基础上，建立了一些电磁波在隧道环境下的传播模型，如单模波导模型、多模波导模型、光学射线模型、双斜率模型、随机数值模型、全波模型等，这些模型各有优缺点[5]。

文献[6]最先提出传播图信道模型；文献[7]采用传播图理论研究了非视距条件下角度域衰落相关性；文献[8]利用图论的信道建模方法，研究室内环境中射线的传播特征；文献[9]利用传播图理论信道建模方法研究了室内无线信道的空时动态特性。

传播图信道建模理论将无线电波在传播过程中所遇到的反射体、散射体以及传播等物理现象建模为计算机科学中的顶点与边的关系[10]，结合频域传递函数的级联特性，得到整个过程的频域信道传递函数。与其他信道建模方法相比，传播图信道建模具有计算量小、结果准确、适用性广的特点。

隧道场景一般分为直射环境与非直射环境。本文针对北京交通大学隧道中心的隧道进行信道测量和仿真，该场景即为非视距环境。经典传播图信道理论通常适用于室内环境等视距场景，但对于该非视距场景不能完全适用，需要针对非视距场景的特殊性作适当修正。

本文针对所研究隧道非视距场景的特点，将隧道散射面划分为多个点集合，在最大反射次数下，计算传播路线中涉及到的点集合间传递函数，并用点集合间转移概率之积调整该路线传递函数，提高建模的准确性。

1 基于传播图的信道建模方法

在传统信道传播环境中，发射机发射的电磁波传播时不可避免地要与障碍物发生反射、折射、衍射等现象。接收机通常放置于远离发射机的位置。信号到达接收机往往要历经多个甚至大量的散射点。这里，用图论把信道传播环境抽象化，点分别代表收发机和散射体，边表示某一点到另一点的传播路径。

每一条从发射机到接收机的路径，都要通过图中的有向边传播，在接收端接收到的信号是所有信号路径之和。在某一条多次反射的传播路径中，信号从发射机发出先到达散射点，并在散射点之间经过若干次反射，最后传到接收机。整个过程中，信号会经历时间色散。为了简化问题，假设信号与散射体之间的作用机制都是线性的，因此信号的时间散射可表示为与一个脉冲响应的卷积，在频域上是与传递函数的乘积。

一般情况下，信号有4种传播方式：视距情况下由发射机到接收机，传递函数用D(f)表示；从发射机到散射点，传递函数用T(f)表示；散射点间反射，传递函数用B(f)表示；散射点到接收机，传递函数用R(f)表示。首先介绍传播图信道建模机制[11]。

传播图是一种特殊的直接图，定义传播图G包含两个集合与两个映射。两个集合(ν，ε)为点集合ν与边集合ε。两个映射为点到边映射init：ν→ε和边到点映射term：ε→ν，边e由起点init(e)和终点term(e)构成。这种情况下，边可表示为e=(init(e)，term(e))。边e∈ε满足init(e)=term(e)，称为环路。图G中一个包含点和边的非空序列〈ν1，e1，ν2，e2，…，eK，νK+1〉称为长度为K的路线。

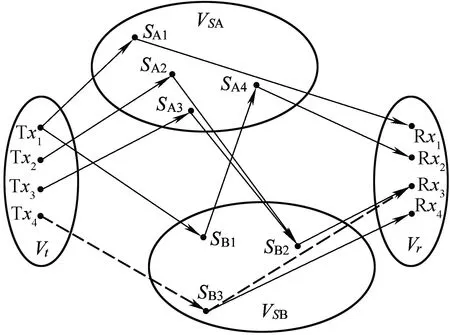
图1 传播图示意图

图1中点分别代表：

发射机Vt={Tx1，…，Tx4}

接收机Vr={Rx1，…，Rx4}

散射点VS=VSA∪VSB={SA1，…，SA4}∪{SB1，SB2，SB3}

图1中虚线表示电磁波传播时某条长度K=2的路线〈Tx4，(Tx4，SB3)，SB3，(SB3，Rx3)，Rx3〉。

在上述场景中，对于某条边e=(ν，ν′)，将其与欧氏距离de=‖rν-rν′‖、增益ge、相位φe、信号沿边e=(ν，ν′)和传播时延τe=de/c联系起来，其中c约为3×108m/s，那么边的传播函数可定义为

(1)

其中相位{φe：e∈ε}在[0，2π)上均匀分布。

不同情况下，边复增益的表达式也不同，一般而言，边的复增益有以下4种情况。

(2)

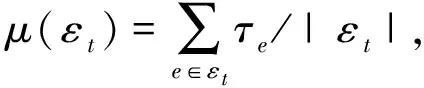
g2/odi(e)是散射点到散射点的功率增益，odi(e)表示从一个散射体到另外一些散射体的边数。这里是能量守恒定理的简化，假定散射体内部功率增益与传播方式无关，仅与周边的反射边数有关[12]。

因此，若已知信道周围散射物的位置尺寸形状信息，即可根据上述方法得到系统传递函数，经过傅里叶逆变换，即可得到CIR。

定义一个经验模型，包含集合{rν}、{ε}和{φe}以及计算传递函数和冲激响应的步骤。顶点坐标在有限区域内R⊂R3，假定发射点和接收点位置均固定，NS个散射点坐标均匀分布在有限区域R上。在传播图理论中，各边之间并非是不相关的，每条边发生的概率也不同。边集合中每条边对应概率Pe，Pe定义为

(3)

第一种情况表示直射环境下的概率；第二、三种情况表示排除从接收端发出的边以及从发射点接收到的边；第四种情况排除了环向路径。

2 传播图信道建模改进

传播图概念的引入可广泛应用于信道建模中，假定散射点间的相互作用在时延上是非色散的，将该理论应用到隧道信道建模中。

经典传播图信道建模理论中，将所有散射点作为一个集合，用统计概率Pvis来描述散射点集合内所有边发生的概率。显而易见，对于不同形状的散射物，统计概率Pvis是不同的。因此，该方法只能粗略描述散射点集合内部的反射情况。

假定电磁波在散射点集合内部不发生散射，在不同散射点集合间可以发生多次反射。根据上述假设，构建隧道几何模型，在隧道壁上均匀分布散射点，然后对隧道中所有散射点划分集合。由于散射点均匀分布在隧道壁上，对散射点集合的划分等效为对隧道散射面的划分。划分散射面的数目越多，涉及到的反射次数越多，仿真结果越精确，相应的计算量也随之增加。

为了研究非视距场景隧道中的无线信道特性，选取弯道隧道进行研究。将隧道散射面划分成10个面，如图2所示，以直道和弯道为分界，在直道和弯道处分别有弧顶、两侧和地面各4个面，包括隧道两端的墙面共10个散射面。其中一部分散射面是平面，一部分散射面是曲面。

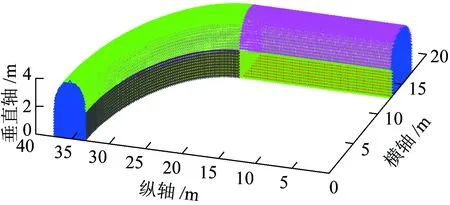
图2 隧道几何模型

电磁波在封闭环境中传播时，往往会经历多次反射。当电磁波在U个散射面之间发生V次反射时，考虑存在电磁波回路情况下，共有UV条可能的传播路线，每条传播路线的传递函数由不同点集合之间的传递函数级联得到。因而总的信道传递函数即为各条传播路线传递函数之和，其表达式为

(4)

(5)

式中：U为考虑V次反射时涉及到面的集合；Hi为第i条传播路线传递函数；Pvis，i为第i条路线发生概率，该路径发生的概率实际上为相邻两点集合之间转移概率之积；Htx，S(1)为发射点集合到第一散射点集合的传递函数；HS(j)，S(j+1)为第j散射点集合到第(j+1)散射点集合的传递函数；HS(V)，rx为第V散射点集合到接收端的传递函数。Pvis，i的计算公式为

(6)

式中：Ptx，S(1)为发射点集合到第一散射集合的转移概率；PS(j)，S(j+1)为第j散射集合到第(j+1)散射集合间的转移概率；PS(V)，rx为第V散射集合到接收端的转移概率。电磁波沿某条路径的发生概率由不同点集合之间的转移概率之积决定。定义点集合之间转移概率的计算公式为

(7)

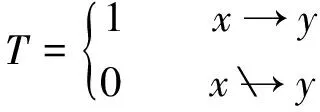
(8)

式中：x，y分别为两个点集合中的元素；X，Y分别为两个点集合中所有元素的个数；T用于判别两个点集合中两点是否相互可见。判断方法如下：连接两点的线段，与所有已知隧道面比较，判断是否有交点，若有交点则视为两点不可见，此时T=0，反之则认为两点可见，此时T=1。判断线段与面是否相交的步骤如下：

步骤1连接两点做一线段，并均匀地在线段上取点。

步骤2判断线段上的点(端点除外)是否位于内部空间内。

步骤3若所有点均位于内部空间，则视为两点可见；反之，若至少有一点不在内部空间中，则认为两点不可见。

通过上述方法，可求得任意两个点集合间的转移概率PS(j)，S(j+1)，即电磁波由一个散射点集合反射到另一个散射点集合的转移概率。相应地可得电磁波沿某条传播路线的发生概率Pvis，i，结合点集合之间的传递函数HS(j)，S(j+1)，便可得该传播路线的传递函数Hi。在设定最大反射次数条件下，将所有路线的传递函数求和，对求和结果做傅里叶逆变换得到CIR。上述方法用点集合间转移概率准确描述信道传播环境，通过细化每条传播路径的发生概率，提高信道建模的准确性。

3 隧道场景下基于图论信道建模

隧道场景在铁路运输、地铁客运等中是一种常见的环境，并且在某一固定场景下周围散射特征相对固定。因此，可以用传播图理论研究隧道中无线信道的传播模型。

3.1 隧道场景描述

本文研究的场景位于北京交通大学隧道中心，平面图与剖面图如图3所示。

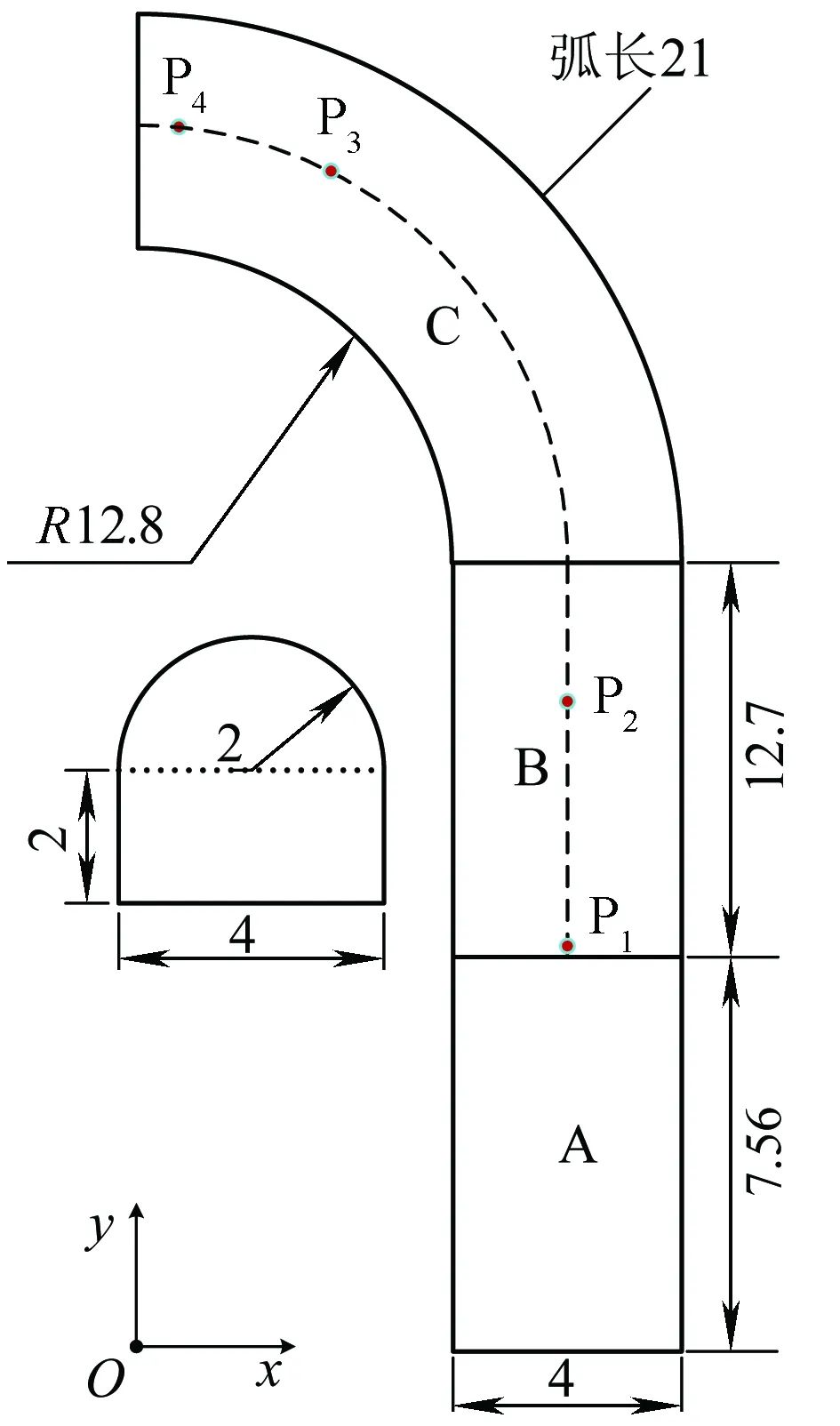
图3 北京交通大学隧道中心平面图和剖面图(单位:m)

该隧道总长度42 m可分为A、B、C 3部分。A部分为长为7.56 m的直道部分，是轨道平台，限于环境原因，该部分不能用于测试。B部分是长度为12.7 m的直道隧道部分。C部分为弯道部分，其内半径为12.8 m，外半径为16.8 m。隧道横截面如图3所示，由半径为2 m的半圆和长4 m、宽2 m的矩形构成。隧道首尾是密封水泥墙面，是一个封闭受限空间。为了下文叙述方便，如图3所示建立直角坐标系，原点位于隧道两端墙面所在平面的交线与地面交点处，图3中虚线表示隧道地面中线。

3.2 验证方案

为了检验本文所提改进方法的正确性，需要将改进方法仿真结果与实际测量结果进行对比。对北京交通大学隧道中心进行宽带信道测量，整个测量系统由信号发射机SMBV100A、双锥全向天线、宽带信道数据采集仪器FSW和全球定位系统GPS(Global Positioning System)同步时钟设备组成，如图4所示。测量频段分为1.4 GHz、1.8 GHz、2.4 GHz和3.5 GHz 4个不同的频点，测量带宽为150 MHz。

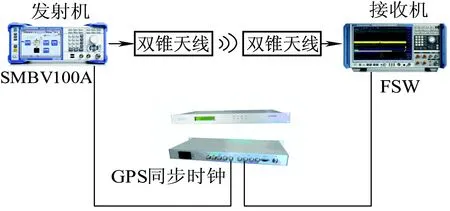
图4 信道测量系统示意图

激励信号源连续产生长度为2 047的ZC(Zadoff-Chu)序列，接收机采集并且存储信号，GPS时钟同步单元保证收发端时钟严格同步。

将接收信号与本地ZC序列做滑动相关得到CIR[13，14]。

(9)

式中：Tb为ZC序列的周期；r(t)为接收信号；c(t)为本地ZC序列；τ为多径时延。

在对实际数据分析过程中，为了得到平均功率时延谱PDP(Power Delay Profile)，取100个CIR快照做平均，表达如下[15]

(10)

式中：h(t，τ)为时变冲激响应；tav为平均时间间隔精度；Δτ为时延精度；n为快照编号；l为平均后的CIR编号；k为时延编号；trep为h(t，τ)采样周期；Lt为对h(t，τ)进行平均的长度。

测试场景如图3所示，信道测量在B区和C区进行。测试过程中收发天线中心均沿着隧道中线。测试在4个位置P1(14.8 m，7.56 m)、P2(14.8 m，15.56 m)、P3(9.22 m，31.84 m)、P4(1.7 m，35 m)进行。

3.3 信道建模仿真

对上述环境利用传播图信道建模理论仿真，步骤如下：

步骤1根据隧道形状与尺寸构建隧道几何模型。

步骤2将隧道散射面划分为10个散射面，计算点集合之间的转移概率。

步骤3对电磁波传播路线进行细化，结合转移概率，得到该路线的传递函数，并用集合间转移概率之积调整传播路线的传递函数。

步骤4将所有路线传递函数求和，做傅里叶逆变换，得到收发天线在某特定频点特定位置处的CIR。

仿真过程中部分参数设置见表1。

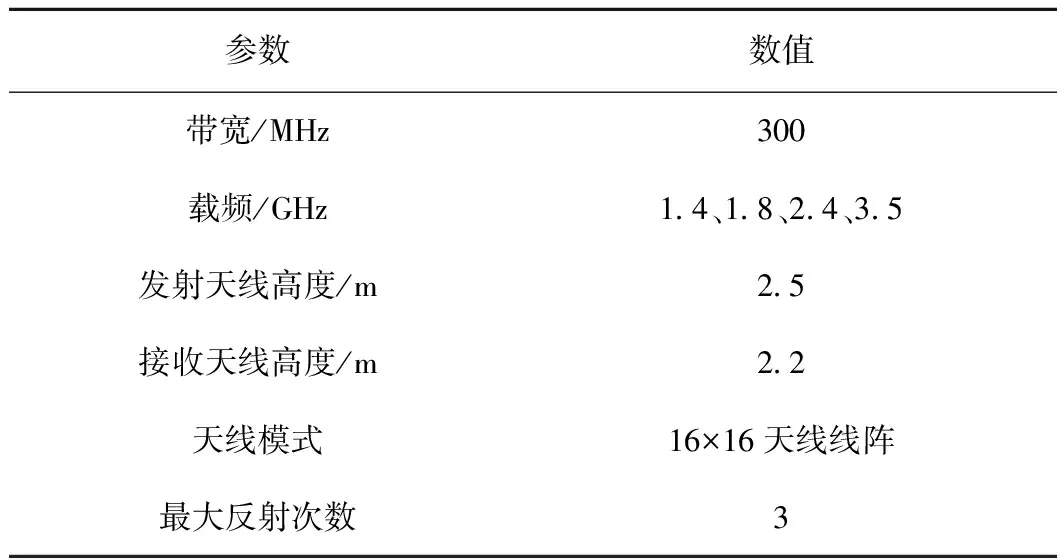
表1 仿真参数设置

图5表示发射机位于P1，接收机位于P3，为非视距环境。图中序号1～12分别表示直道底部散射点集合、弯道底部散射点集合、直线左侧散射点集合、弯道左侧散射点集合、直线右侧散射点集合、弯道右侧散射点集合、直线顶部散射点集合、弯道顶部散射点集合、后墙散射点集合、前墙散射点集合、发射天线点集合、接收天线点集合。

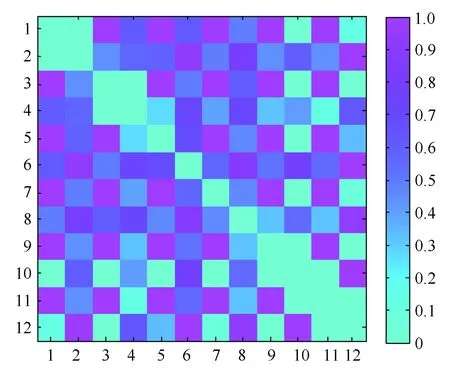
图5 非视距转移概率矩阵

从图5可以看出：

(1)矩阵对角线元素为0，环向路径的转移概率为0，即在一次反射前提下，电磁波由一个点集合传播到自身的概率为0。

(2)直道部分视距场景内散射点集合间转移概率较高，弯道部分非视距场景内散射点集合间转移概率较低。

(3)电磁波沿某条路线传播时经历的反射次数越多，涉及到的散射点集合越多，相应的该路线发生概率越低。

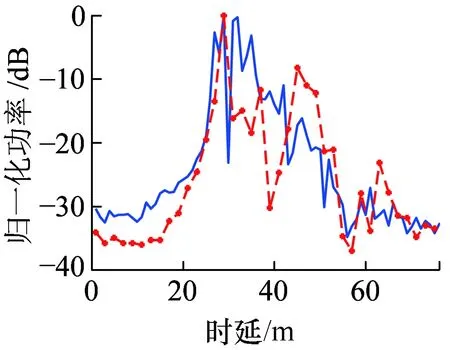
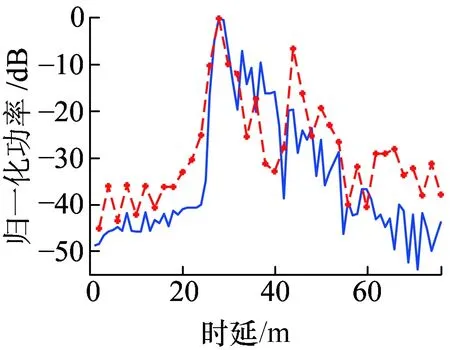
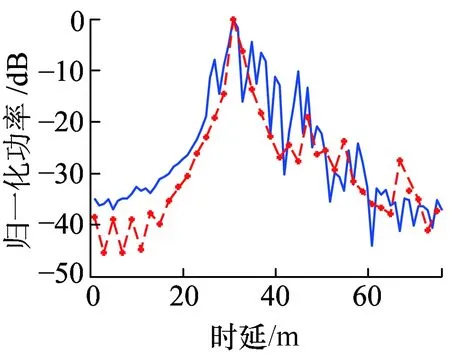
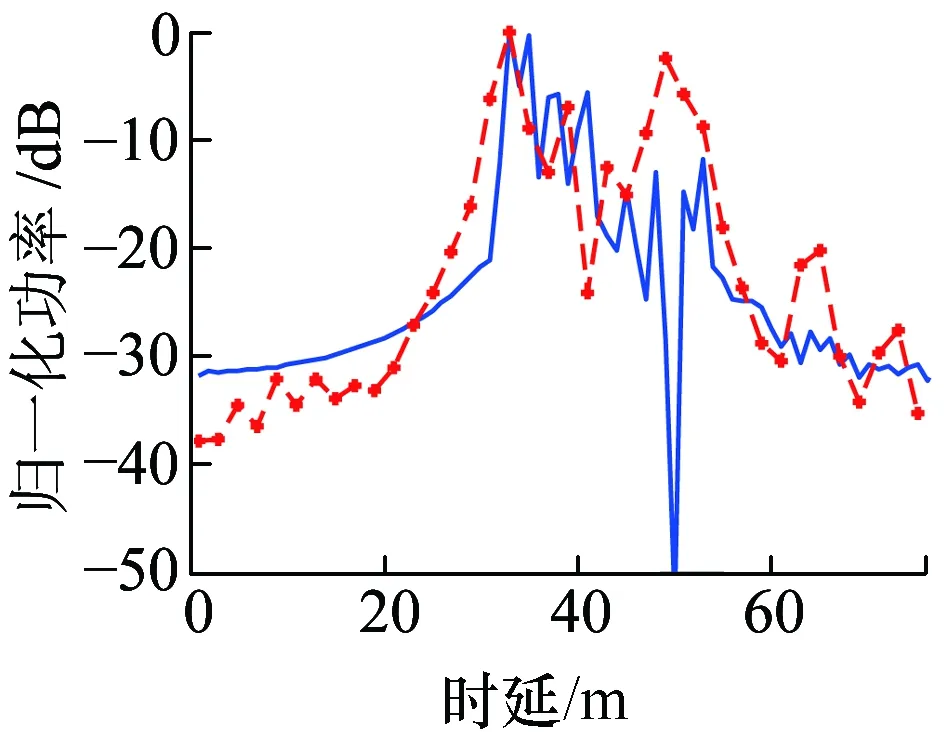
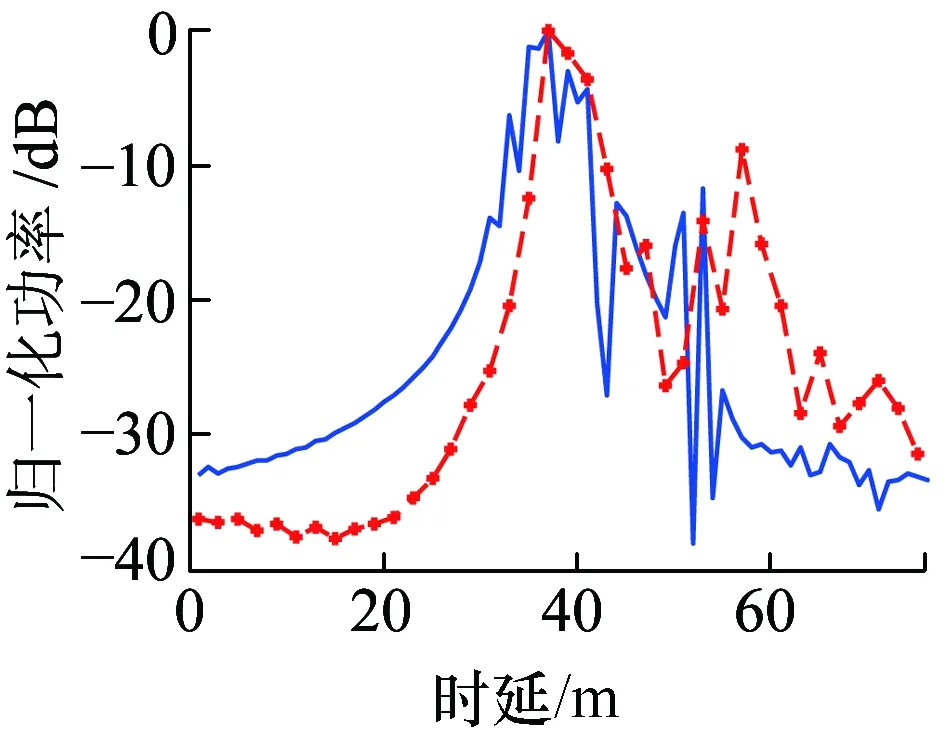
实际信道测量过程中，发射机位于P1，接收机分别位于P3、P4。在距离发射机不同位置处，g=0.7时得到的PDP如图6、图7所示。

(a)频点1.4 GHz

(b)频点1.8 GHz

(d)频点3.5 GHz图6 接收机位于P3时归一化PDP仿真结果与实测结果

(a)频点1.4 GHz

(b)频点1.8 GHz

(c)频点2.4 GHz

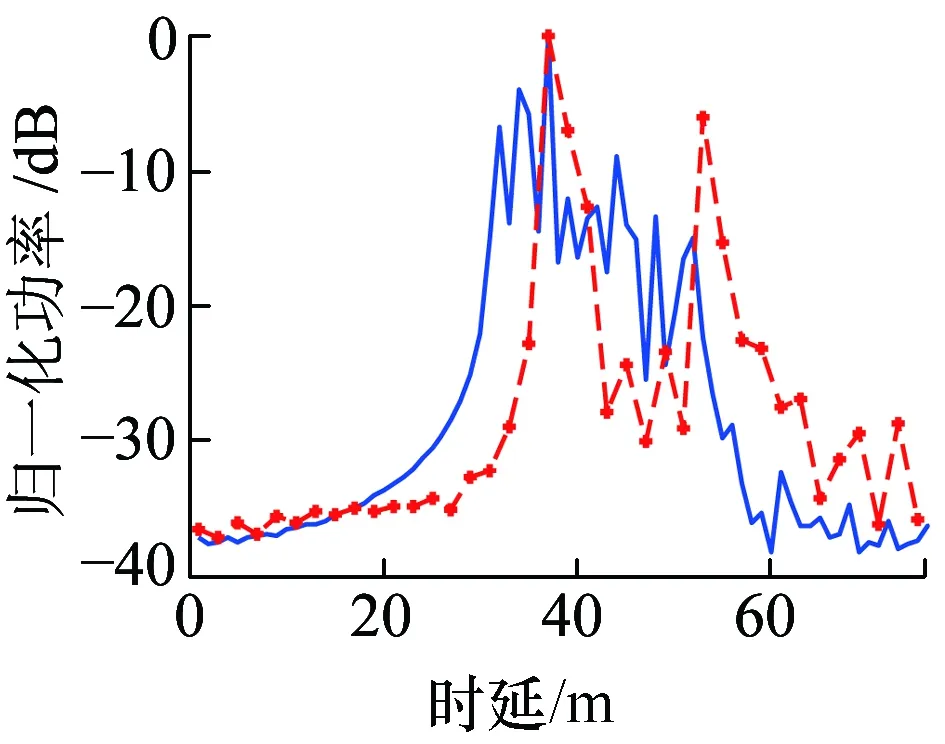
(d)频点3.5 GHz图7 接收机位于P4时归一化PDP仿真结果与实测结果

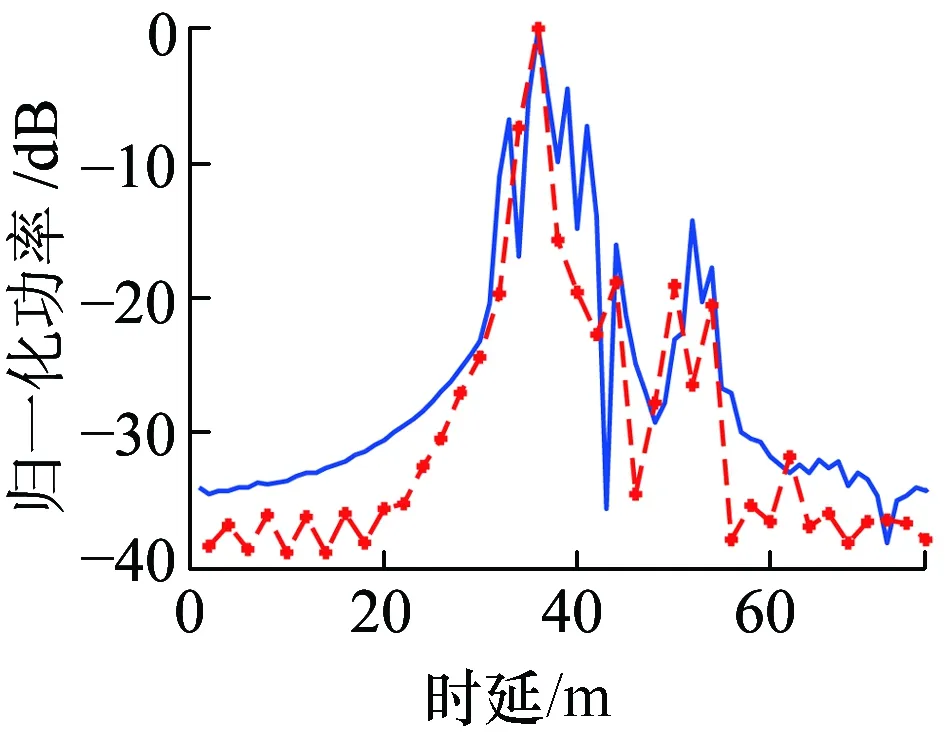
在图8中，发射机位于P1，接收机位于P3，仿真频点2.4 GHz，带宽300 MHz，可知横轴上每个单位时延的等效距离为1 m。结合隧道平面图可知，此环境为非视距情况，A处峰值处位于29 m处，表示最先到达信号，功率最高。B处距离A处峰值信号约15 m，是A区长度的两倍，表示信号经过后墙反射后到达接收端。从图8可以看出，A与B部分测量结果与仿真结果比较吻合，两者差距在10 dB范围内。但是随着时延增加，差距逐渐增大到20 dB乃至30 dB，吻合欠佳，这是因为实际测量中环境复杂，除去人员干扰因素，测量环境中摆放着一些散射物体，仿真过程中无法全部表示出来。

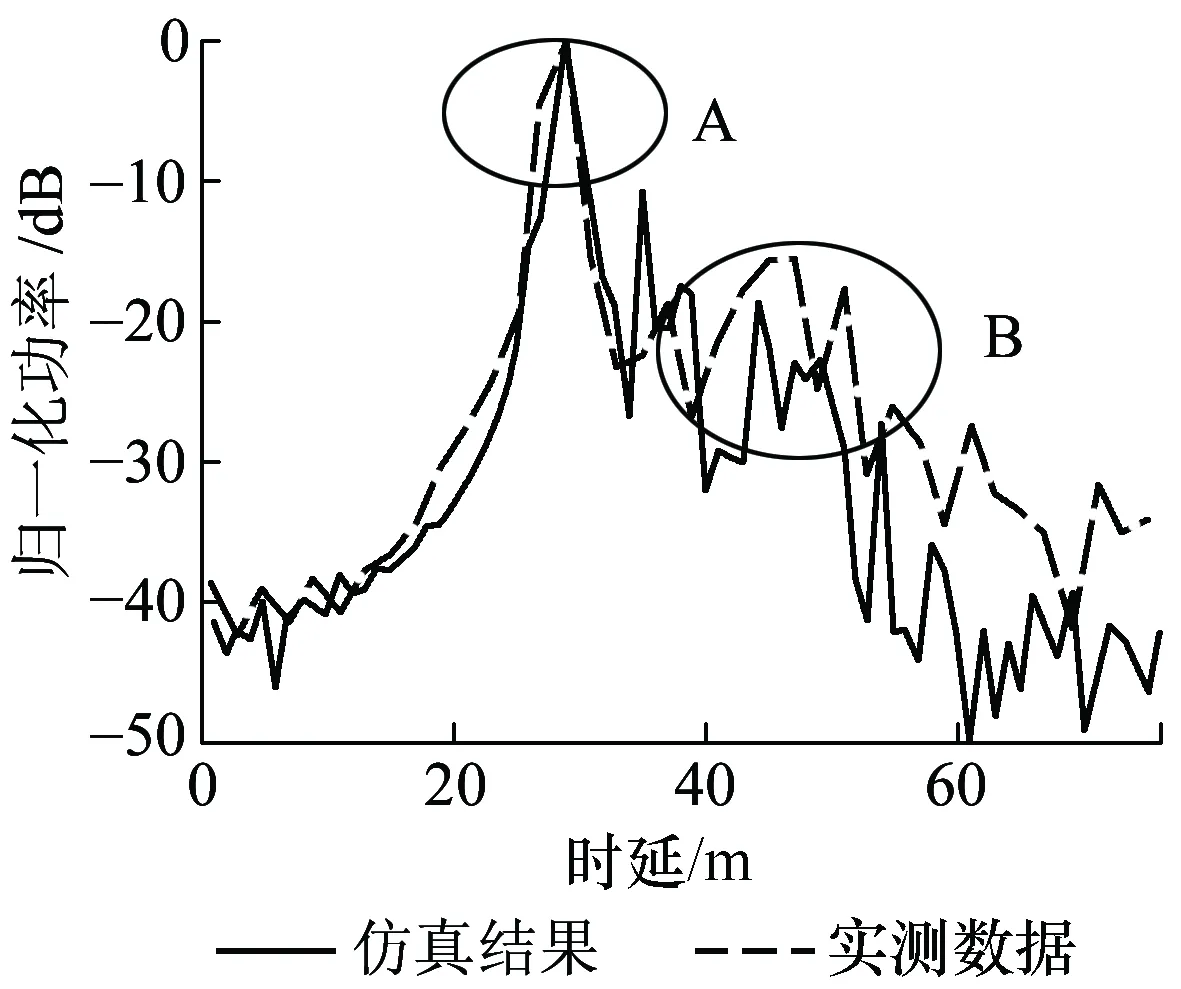
图8 归一化PDP

统计图6、图7中归一化PDP仿真结果与实测结果之间的差值，可得两者功率误差分布图如图9所示。

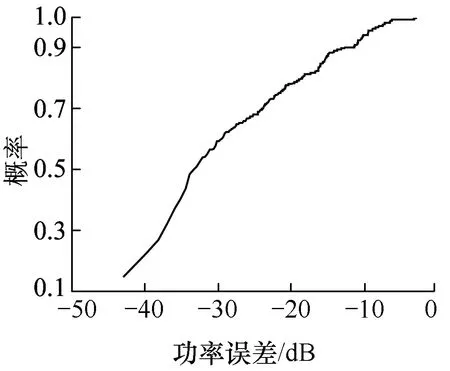
图9 功率误差分布图

由图9可知，误差-10 dB以内的抽头占据了约90%，因此可认为改进的传播图建模方法在不同频点不同位置的仿真结果与实测结果基本一致。说明所提方法是合理的，这里用改进方法进一步研究隧道无线信道。

3.4 MIMO信道仿真

在N个发射端天线，M个接收端天线的两个均匀线性天线阵列情况下，描述发射端到接收端的宽带多输入多输出MMO(Multiple Input Multiple Output)无线信道矩阵，可以表示为

(11)

(12)

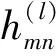
(13)

由于天线空间相关系数的计算，可求得任意两条链路间的相关系数。对于N×M天线MIMO系统，天线ni和nj间的空间相关系数为

(14)

因此，信道相关矩阵为

(15)

从图10可以看出，发射端天线间的相关性整体在0.4～0.9范围内，下降趋势平滑，根据文献[16、17]可知，角度扩展较小，相关性下降趋势越平滑。接收端天线间的相关性整体在0.1～0.6，有一定的波动性，角度扩展较大。波动周期为一个波长，随着天线间距的增加而逐渐递减。

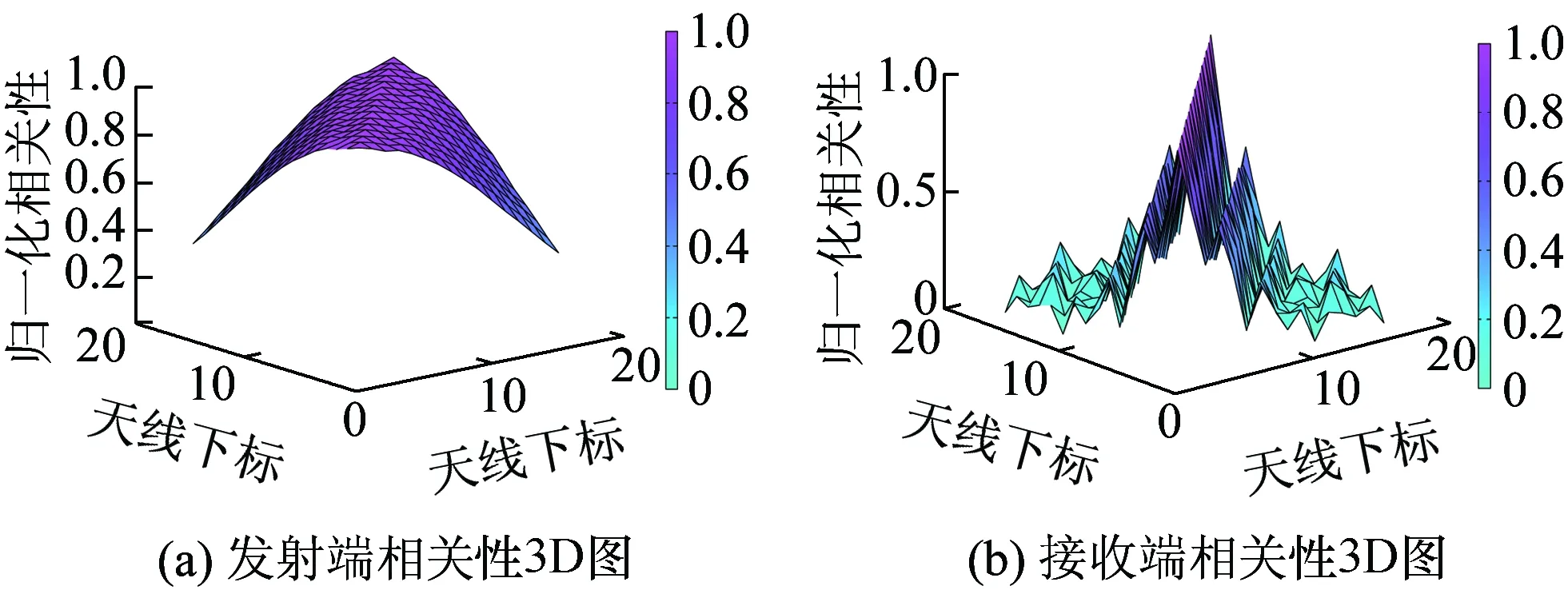
图10 收发天线相关性3D图

3.5 合理性验证

采用空间交替广义期望最大化SAGE(Space-Alternating Generalized Expectation-maximization)算法[18]从CIR中提取信道参数：幅度、离开角AOD(Angle of Departure)、到达角AOA(Angle of Arrival)、时延和多普勒频移。利用这些信道参数重构CIR，可得收发天线间相关性3D图如图11所示。对比图8可以看出，两者趋势相同，相关性大小也基本一致，间接说明提取参数的合理性与正确性。

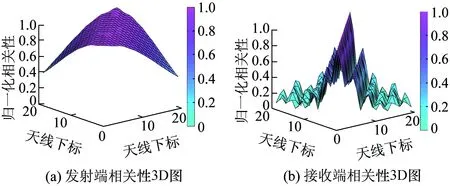
图11 重构CIR的相关性3D图

通过传播图信道建模理论仿真得到CIR，采用SAGE算法进行处理，得到幅度、AOD、AOA、时延等信道参数，相应的角度功率谱PAS(the Power Angle Spectrum)如图12所示。

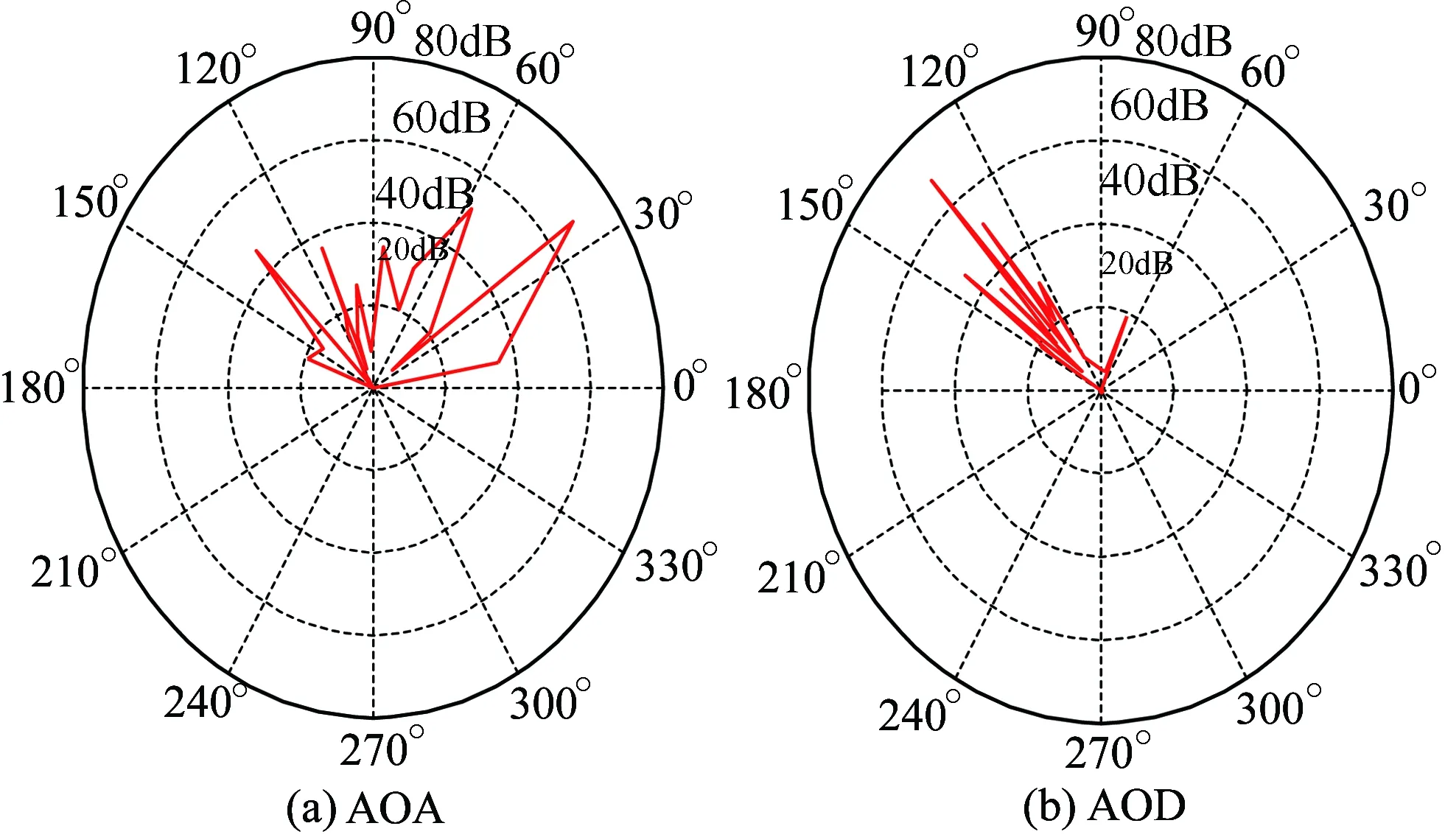
图12 AOA与AOD的PAS

角度扩展计算结果如下：AOD角度扩展ΔSAGE_aod=6.6°，AOA角度扩展ΔSAGE_aoa=31.9°。从AOD的PAS图中可以看出AOD集中分布在125°～145°，AOA分布在10°～160°。由于电磁波在到达接受天线时在隧道内经历了丰富的反射，来波到达接收天线的方向并不唯一，而是呈发散状，导致AOA的角度扩展较大。如图13所示，电磁波从发射阵列天线P4发射，历经C区散射点、B区散射点后，以多种不同的角度到达接收天线，致使AOA的角度扩展较大。

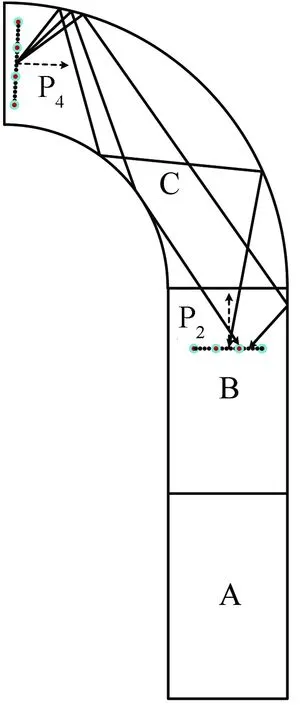
图13 反射示意图

3.6 多天线信道容量

根据香农理论，在高斯白噪声下无记忆MIMO系统信道最大容量计算公式为[19]

C=lg[det(IM+σHHH)]

(16)

式中：σ为每个接收天线上的平均信噪比SNR(Signal Noise Ratio)；I表示单位矩阵；上标H表示矩阵的共轭转置；C的单位为bit/(s·Hz)。

在上述环境下，设定SNR为10 dB，采用蒙特卡罗方法对1×1、2×2、4×4、8×8以及16×16天线阵列信道容量仿真。对比瑞利信道容量，结果如图14所示，实线表示瑞利信道容量累计概率分布曲线，虚线表示仿真结果。

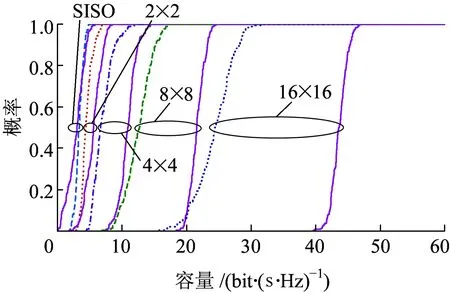
图14 信道容量累计概率分布

从图14可以看出，随着天线数目的增加，隧道环境下遍历容量与瑞利信道遍历容量的差距越来越大。这种现象一方面是由于隧道环境内丰富的反射使得接收天线信号间的相关性较高；另一方面，从图15可以看出，随着天线数目增加，假定以-16 dB(0.025)为基准，归一化奇异值小于基准线的数目越来越多，H矩阵发生退化，相应的信道容量也有所下降。

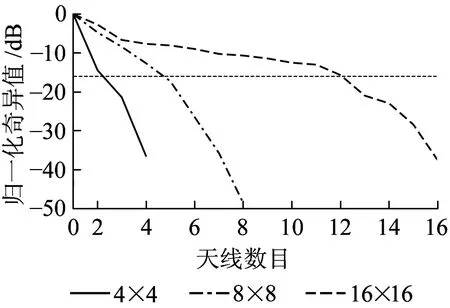
图15 多天线归一化奇异值分布

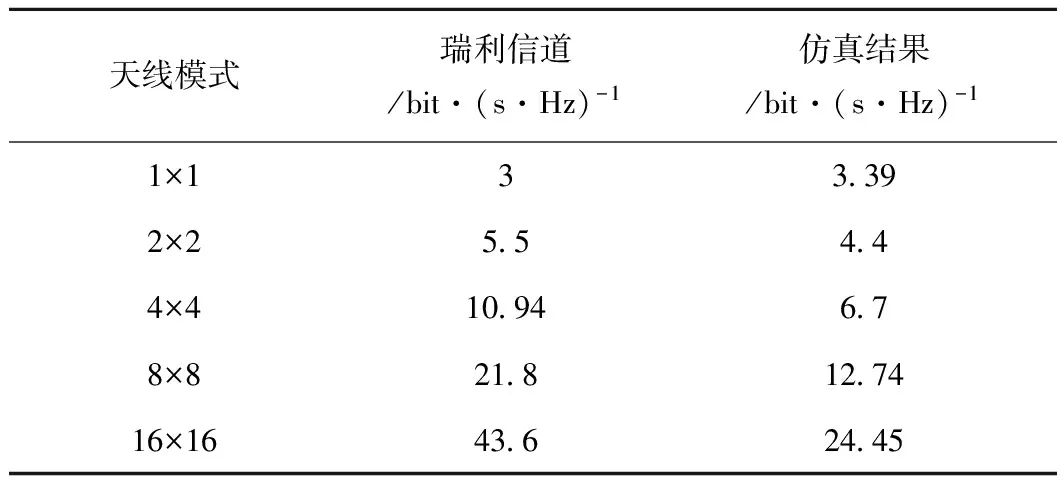
表2 不同参数下信道遍历容量

4 结束语

本文在传播图信道建模理论基础上，对隧道环境下无线信道建模进行研究。通过从细化散射点到散射点传递函数的角度提高信道建模精度，利用划分的散射面的排列表示传播路线，将路线上相邻两点集合间的子传递函数级联，并利用相邻两集合间的转移概率之积调整该路线的传递函数。对比实际环境下的信道测量结果，两者基本一致。并进一步分析了隧道环境下多天线相关性、AOA与AOD分布、容量等信道特征参数。因此可以把该方法应用于非视距隧道环境下无线信道的建模与仿真。

参考文献：

[1]洪开荣.我国隧道及地下工程发展与展望[J].隧道建设,2015,35(2):95-107.

HONG Kairong.State-of-art and Prospect of Tunnels and Underground Works in China[J].Tunnel Construction,2015,35(2):95-107.

[2]刘留,陶成,陈后金,等.高速铁路无线传播信道测量与建模综述[J].通信学报,2014,35(1):115-127.

LIU Liu,TAO Cheng,CHEN Houjin,et al.Survey of Wireless Channel Measurement and Characterization for High-speed Railway Scenarios[J].Journal on Communications,2014,35(1):115-127.

[3]DUDLEY D G.Mathematical Foundations for Electromagnetic Theory[M].New York:IEEE Press,1994.

[4]MAHMOUD S F.Electromagnetic Waveguides:Theory and Applications[M].Lodon:IET Digital Library,1991.

[5]FOROOSHANI A E,BASHIR S,MICHELSON D G,et al.A Survey of Wireless Communications and Propagation Modeling in Underground Mines[J].IEEE Communications Surveys & Tutorials,2013,15(4):1 524-1 545.

[6]PEDERSEN T,FLEURY B H.A Realistic Radio Channel Model Based in Stochastic Propagation Graphs[C]//5th Conference on Mathematical Modelling(MATHMOD 2006).Forlag Uden Navn,2006:324-331.

[7]YIN X,LIANG J,FU Y,et al.Preliminary Study on Angular Small-scale Cross-correlation of Channels in NLOS Scenarios Using Propagation Graphs[C]//International Workshop Broadband MIMO Channel Measurement Modeling(IWonCMM),2011.

[8]UGUEN B,AMIOT N,LAARAIEDH M.Exploiting the Graph Description of Indoor Layout for Ray Persistency Modeling in Moving Channel[C]//2012 6th European Conference on Antennas and Propagation(EUCAP).New York:IEEE Press,2012:30-34.

[9]ZHANG R,LU X,ZHONG Z,et al.A Study on Spatial-temporal Dynamics Properties of Indoor Wireless Channels[C]//Wireless Algorithms,Systems,and Applications.Berlin:Springer Berlin Heidelberg,2011:410-421.

[10]CHENG W,TAO C,LIU L,et al.Geometrical Channel Characterization for High Speed Railway Environments Using Propagation Graphs Methods[C]//2014 16th International Conference on Advanced Communication Technology(ICACT).New York:IEEE Press,2014:239-243.

[11]PEDERSEN T,FLEURY B H.Radio Channel Modelling Using Stochastic Propagation Graphs[C]//2007 IEEE International Conference on Communications. New York: IEE Press,2007:2 733-2 738.

[12]和雨佳，陶成.基于LTE高速环境下无线信道测量和建模关键技术的研究[D].北京：北京交通大学，2013.

[13]周涛,陶成,刘留,等.基于测量的高铁宽带无线信道莱斯K因子研究[J].铁道学报,2013,35(9):72-78.

ZHOU Tao,TAO Cheng,LIU Liu,et al.Measurement-based Research on Ricean K-factor of Broad-band Wireless Channel in High-speed Railway Scenarios[J].Journal of the China Railway Society,2013,35(9):72-78.

[14]刘留,陶成,邱佳慧,等.高速铁路宽带无线信道测量方法研究[J].铁道学报,2011,33(5):48-53.

LIU Liu,TAO Cheng,QIU Jiahui,et al.Research on Broadband Wireless Channel Sounding Methods for High-speed Railway[J].Journal of the China Railway Society,2011,33(5):48-53.

[15]邱佳慧,陶成,刘留,等.U型槽无线信道多径传播特性测量与建模方法的研究[J].铁道学报,2014,36(1):40-48.

QIU Jiahui,TAO Cheng,LIU Liu,et al.Research on Measurement and Modeling of Wireless Channel Multipath Propagation Properties for U-Shape Cutting[J].Journal of the China Railway Society,2014,36(1):40-48.

[16]杨大成.移动传播环境:理论基础·分析方法和建模技术[M].北京:机械工业出版社,2003.

[17]PEDERSEN K I,ANDERSEN J B,KERMOAL J P,et al.A Stochastic Multiple-input-multiple-output Radio Channel Model for Evaluation of Space-time Coding Algorithms[C]//Vehicular Technology Conference,2000.IEEE-VTS Fall VTC 2000.New York:IEEE Press,2000,2:893-897.

[18]FLEURY B H,JOURDAN P,STUCKI A.High-resolution Channel Parameter Estimation for MIMO Applications Using the SAGE Algorithm[C]//International Zurich Seminar on Broadband Communications,Access,Transmission,Networking.New York:IEEE Press,2002.

[19]LIENARD M,DEGAUQUE P,BAUDET J,et al.Investigation on MIMO Channels in Subway Tunnels[J].IEEE Journal on Selected Areas in Communications,2003,21(3):332-339.