基于SPN的铁路时间同步网建模与性能分析

张友鹏，李天娇，王 锋，张 珊，兰 丽

(兰州交通大学 自动化与电气工程学院，甘肃 兰州 730070)

随着铁路列车运行速度的提高以及短时间内的跨线跨区行驶，涉及行车安全的铁路内部系统时间的准确性和统一性变得十分重要。尤其是在铁路系统引入综合网管之后，将系统告警全部纳入监管范围，这就对系统内部的时间同步提出了更加严格的要求。如果时间不同步，那么在故障发生时，就不能对故障进行快速准确的定位，影响综合网管对故障的判断处理，进而影响列车的运行效率[1，2]。根据调查统计显示，铁路内部系统中存在的偏差较大，检测发现有的偏差大于17 min，严重影响铁路运营调度指挥、故障定位分析处理等[3]。针对上述情况，铁路系统内部建立了时间同步网，为铁路运输各系统提供统一、准确的时间信息。但是，目前针对铁路时间同步网的研究较少，文献[4]对铁路时间同步进行概述，介绍了铁路时间同步网的现状、结构及发展规划；文献[5]通过对铁路时间同步网的介绍，提出了该网络的性能指标，同时搭建了模拟仿真平台，进行测试研究；文献[6]介绍了京津铁路客运专线工程时间同步系统和各级母钟的功能要求。上述文献仅对铁路时间同步系统进行概述，提出其指标要求，并未对该在建网络的性能进行分析。

铁路时间同步网的主要性能指标有绝对守时准确度和同步周期，对绝对守时准确度影响较大的是延时、故障随机性和同步周期设置。针对上述问题选取适合的建模分析方法，其中随机Petri网SPN(Stochastic Petri Nets)具有较好的描述能力，易于描述系统中并发、异步、分布式和随机性等特征，而且便于描述时间的随机性[7-9]。本文采用随机Petri网对铁路时间同步网进行性能分析，分析在各故障因素的影响下，客户端能正确同步时间源的概率以及同步周期对绝对守时准确度的影响。通过明确各性能指标的关系，进而选取合适的参数，使网络性能达到使用要求。

1 铁路时间同步网及时间同步协议

1.1 铁路时间同步网结构

铁路时间同步网分为两个部分，地面时间同步和列车时间同步。地面时间同步网分为三级，一、二、三级时间同步设备分别设置在中国铁路总公司调度中心、铁路局调度所和车站。该网络的设备主要有卫星接收设备、母钟设备、时间显示设备、网管系统和传输链路[10]，系统构成示意图如图1所示。

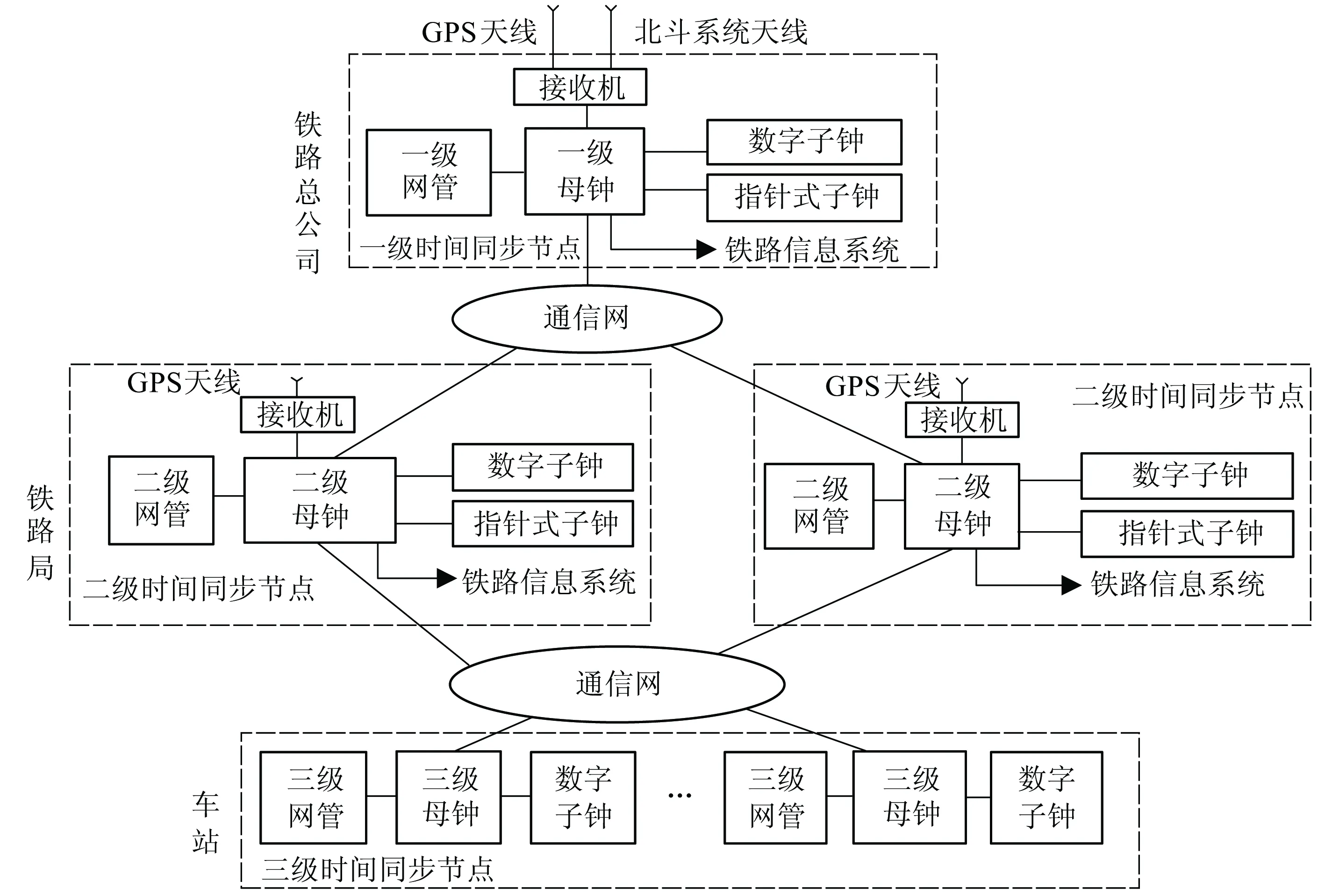
图1 铁路时间同步网系统构成示意图

铁路时间同步网采用三级主从同步式结构，在同步过程中位于铁路总公司一级时间同步节点的接收机接收GPS/北斗信号，进行对比，输出较为精确的时间信号给一级母钟，一级母钟周期性地将时间信号传送给位于各铁路局的二级母钟。二级母钟接收时间信号，计算时延和时间偏差后更新本机时间，并周期性地将时间信息传送给位于各站段的三级母钟。三级母钟接收时间信息，计算时延和时间偏差后更新本机时间。一、二、三级母钟同时还为需要时间信息的其他节点提供时间信息，这样就实现了系统内时间同步，完成了同步过程。铁路时间同步网各级之间采用网络时间协议NTP(Netwrok Time Protocol)进行时间同步，并且时间同步只允许从高级节点接收信息，不允许同级之间相互传送时间信息。

1.2 NTP时间同步协议

由于NTP协议具有应用方便、不需要硬件支持等特点，被广泛应用于系统时间同步中，但NTP协议的守时精度也受到各种因素的影响，最关键的影响因素是网络延时的随机性，这种随机性导致了时钟延时和偏差计算的不准确。铁路时间同步网各级之间采用NTP协议中的Client/Server模式同步时间信息，其对时原理如图2所示。用θ表示客户端和服务器之间的时间偏差；用δ表示对时过程中两端的链路延时，从客户端到服务器的链路延时为δ1，从服务器到客户端的延时为δ2。

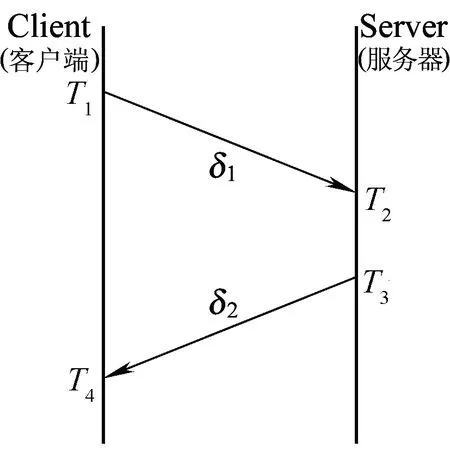
图2 NTP协议对时原理

如图2所示，客户端每隔固定的时间向服务器发送时间同步请求报文，该请求报文中包括了客户端发送报文的时间T1；服务器接收到请求报文，向客户端发送响应报文，该响应报文包括T1、服务器接收到请求报文的时间T2、服务器发出响应报文的时间T3；客户端接收到响应报文后再打上本机接收时间T4[11]，根据这4个时间戳可以得出

(1)

则时间偏差为

(2)

而NTP协议计算时间偏差是假设服务器与客户端的往返路径相同，即δ2=δ1，但是网络传输的往返路径很多时候是不对称的，这样的假设造成了时间偏差计算不准确，所以实际的时间偏差与协议近似计算的时间偏差相差(δ2-δ1)/2，由此可知绝对守时准确度可近似为(δ2-δ1)/2。

2 随机Petri网

2.1 随机Petri网的定义

根据随机Petri网建立铁路时间同步网模型进行分析，应首先明确其定义和分析方法。

定义：一个随机Petri网定义为七元组

∑=(P，T，F，V，K，M0，λ)

(3)

式中：P={p1，p2，…，pn}为库所集合；T={t1，t2，…，tn}为变迁集合；P∩T=Ø，P∪T≠Ø；F=(P×T)∪(T×P)，为流关系(关系弧),W∶F→Z+为流关系的权函数，Z+={1，2，3…}为关系弧的权重；K∶P→Z+∪{ω}是库所中的容量函数，ω为无穷大数；M0为初始标记向量；λ={λ1，λ2，…，λm}是变迁实施速率的集合，λi表示在变迁允许实施情况下的变迁实施速率，和指数分布概率密度函数f(x)=λe-λx中的λ是等价的。

τi是变迁的平均实施延时或者平均服务时间，其值为平均实施速率的倒数，即τi=1/λi。每个λi的值都具有实际的物理意义，一般是在所描述系统的实际测量中获得或者为根据某种要求的预测值[12]。

库所和变迁由有向弧进行连接，库所代表系统运行过程中的某个局部状态，变迁则代表时间。当库所包含标记时表示满足某种条件或者到达某种状态。将所有含有标记的状态组成集合，就代表了系统运行的全局状态。当所有的前提条件满足，即库所中含有标记时，则变迁可以实施。

2.2 随机Petri网模型的性能分析方法

根据所建模型，通过以下步骤可以计算得出网络的平均延时时间δ，进而计算出在不同同步周期下的绝对守时准确度。

(1)标记概率密度

标记概率密度表示在稳定状态下，每个库所中含有标记数的概率。对∀s∈S，∀i∈N，令P[M(s)=i]表示库所s中含有i个标记的概率，则可求得位置s的标记概率密度函数为

(4)

式中：Mj∈[M0>且Mj(s)=i[13]。

(2)在位置中的平均标记数

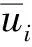
(5)

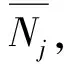
(6)

(3)变迁的标记流速

∀t∈T的标记流速是指单位时间内流入t的后置库所s的平均标记数R(t，s)，则

R(t，s)=W(t，s)×U(t)×λ

(7)

式中：λ为t的平均实施速率。

(4)平均延时时间

根据Little规则和平衡原理可以得到

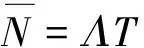
(8)

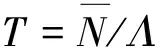
(9)

3 铁路时间同步网的SPN模型

根据铁路时间同步网结构与所用时间同步协议，建立铁路时间同步网一二级节点之间的信息传输和故障处理模型，如图3所示，模型中库所和变迁的含义见表1、表2。

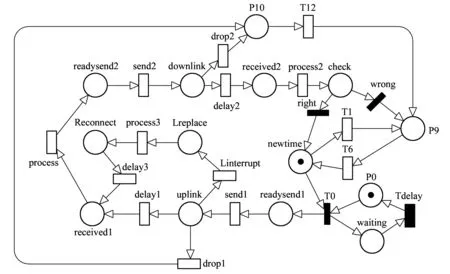
图3 铁路时间同步网模型

表1 模型中库所的含义

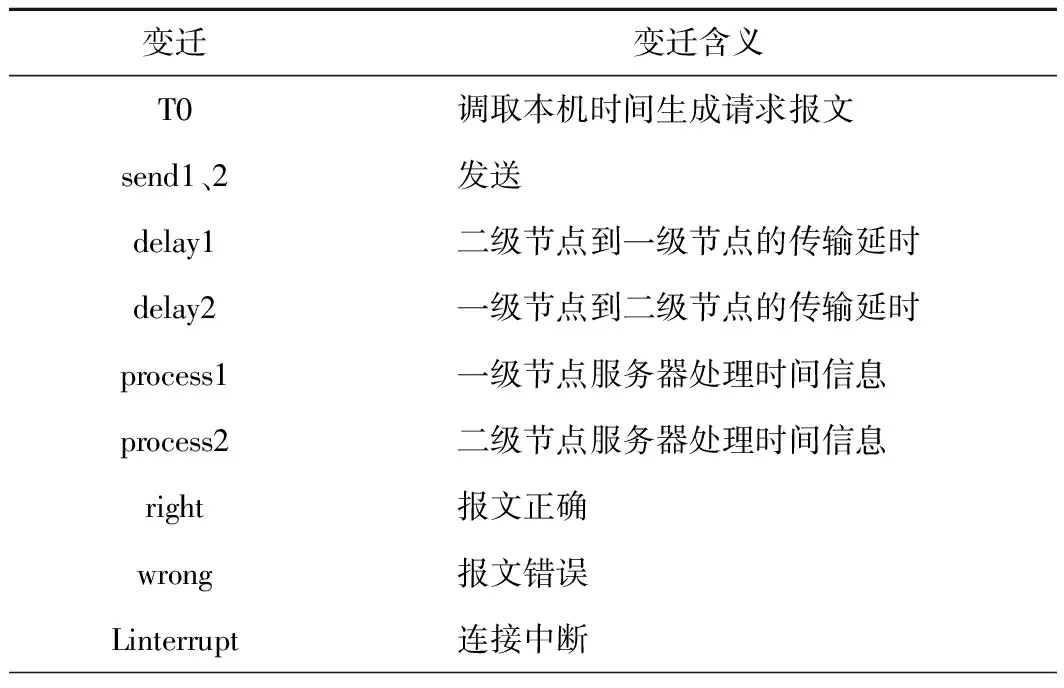
表2 模型中变迁的含义

续上表

在模型中，位于铁路局的二级时间服务器每隔规定的同步周期Tdelay调取本机时间，产生时间请求报文，并向一级节点发送，请求报文进入上行链路uplink，经过网络延时delay1到达位于铁路总公司的一级节点；一级节点接收received1二级节点的请求报文，进行处理process1，打上接收时间和发送时间，向客户端发送时间响应报文，时间响应报文进入下行链路downlink，经过网络延时到达二级节点；二级节点接收响应报文后，经过处理判断其信息的正确合法性，如果正确通过计算得到延时偏差，更新本机时间，如果错误将报文丢弃进入守时状态，等待下一周期的对时请求。在通信传输中有可能发生连接中断的情况，针对这种情况铁路采用双冗余环形网络，在发生连接中断Linterrupt后，进行链路倒换Lreplace处理，通过Reconnect重新连接，经过新的链路延时到达一级节点。两条链路同时发生链路倒换的概率较小，并对守时准确度的影响较小，所以该模型假设只有上行链路可能发生连接中断。在通信过程中还可能发生丢包故障，当发生这种故障时客户端直接进入守时状态，等待下一周期对时请求。

铁路时间同步的时间信息传递由铁路通信传输网承载，结合故障因素和通信机制建立模型，其中传输参数参考铁路通信传输网。

模型中的变迁delay1表示由发送端到接收端的网络延时，根据《IP网络技术要求——网络性能参数与指标》规定[14]，网络端到端的平均传输时延应小于150 ms，传输时延变化在50 ms左右，根据铁路数据业务的要求，平均传输延时应小于80 ms，延时变化在50 ms左右，所以其上行链路延时参数设为0.08，下行链路延时参数设为0.13。

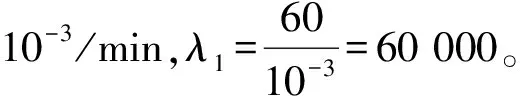
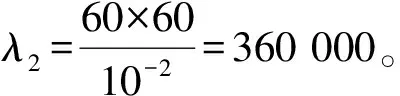
Tdelay为同步周期，即当客户端向服务器发出请求报文后，到下一次发送请求报文的时间。本文将其定为1 s、2 s、3 s、5 s、10 s、20 s、24 s、60 s、80 s、100 s、120 s、140 s、160 s、180 s、200 s、220 s、240 s、260 s、280 s、300 s、360 s，进而计算发报周期与绝对守时准确度的关系。

4 铁路时间同步网性能分析

对该网络性能进行分析，其性能指标包括网络平均延时、同步周期、资源利用率、绝对守时准确度以及各指标之间的关系。绝对守时准确度是指当有时间信号传送到时间同步系统中时，时间同步设备输出接口的时间相对UTC的偏差。该指标用于衡量被测时间同步设备与其时钟源设备的相对时间偏差是否符合要求，如果守时准确度超过要求的标准，要通过缩短同步周期来提高精度[5]。

根据铁路时间同步网所用时间同步协议NTP的工作原理，绝对守时准确度可近似为(δ2-δ1)/2，根据铁路时间同步网的模型，利用2.2节所述随机Petri网的性能分析计算方法，分别在上述同步周期中计算出上行和下行链路的延时δ1与δ2，而后计算出绝对守时准确度，得到同步周期与绝对守时准确度的关系如图4所示。

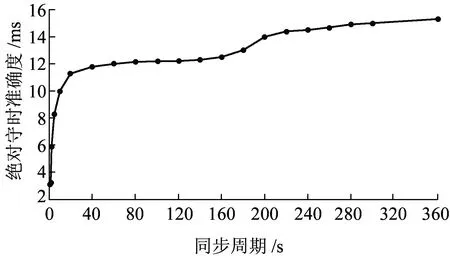
图4 同步周期与绝对守时准确度关系图

从图4可以看出，随着同步周期的增大绝对守时准确度增大，同步周期在1～20 s时，绝对守时准确度急剧增加，20 s后增加趋于平缓。上述所求同步周期与绝对守时准确度关系符合文献[5]的测试结果，验证了模型的正确性，并且可以看出，同步间隔设置的越小，同步的精度越高，但同步周期设置过小会引起网络延时增加，拥塞程度加重，造成同步困难[16]。所以综合考虑同步周期与绝对守时准确度，建议二级节点同步周期设置为180 s。

由此设置二级节点同步周期为180 s，在TimeNET中定义仿真执行措施如下：

R1：P{#newtime=1}为客户端正确同步于服务器的概率；R2：P{#uplink=1}为上行链路的链路资源利用率；R3：P{#downlink=1}为下行链路的链路资源利用率；R4：P{#drop=1}为发生丢包的概率；R5：P{#Lreplace=1}为发生链路中断的概率[17]。

对模型进行性能分析，利用软件中的Transient仿真方法，设定结束时间为1 000 s，进行仿真，得出R1的概率为99.82%，客户端能正确同步服务器的概率如图5所示。图中上下两条线表示概率的波动范围，中间线表示计算出的实际概率曲线。可以看出，R1在100%附近波动，表示客户端时间正确地同步于服务器的概率接近于100%。

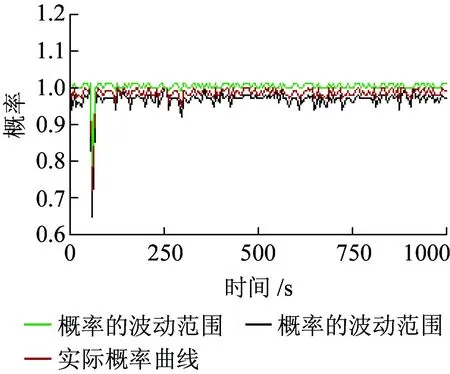
图5 客户端与服务器正确同步概率

由于发生故障的概率较小，并且时间信息占用资源较小，当同步周期设置为180 s时，即每隔180 s才执行同步请求，这样很难看出发生故障的概率和占用的资源，所以将同步周期缩小18倍，结束时间设为1 000 s，R2、R3是衡量uplink、downlink状态的执行措施，即仿真得出链路的资源利用率，R2的概率为0.79%，R3的概率为1.29%。仿真结果如图6所示。

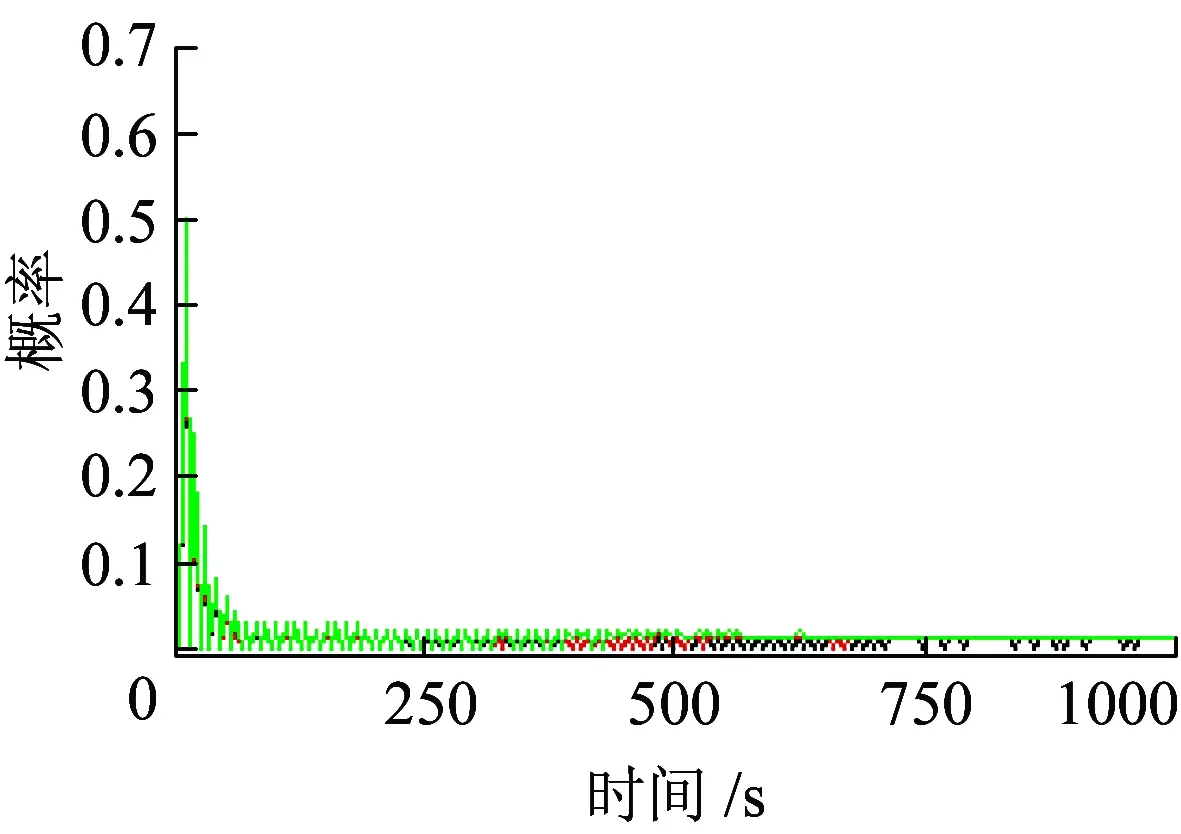
(a)上行链路

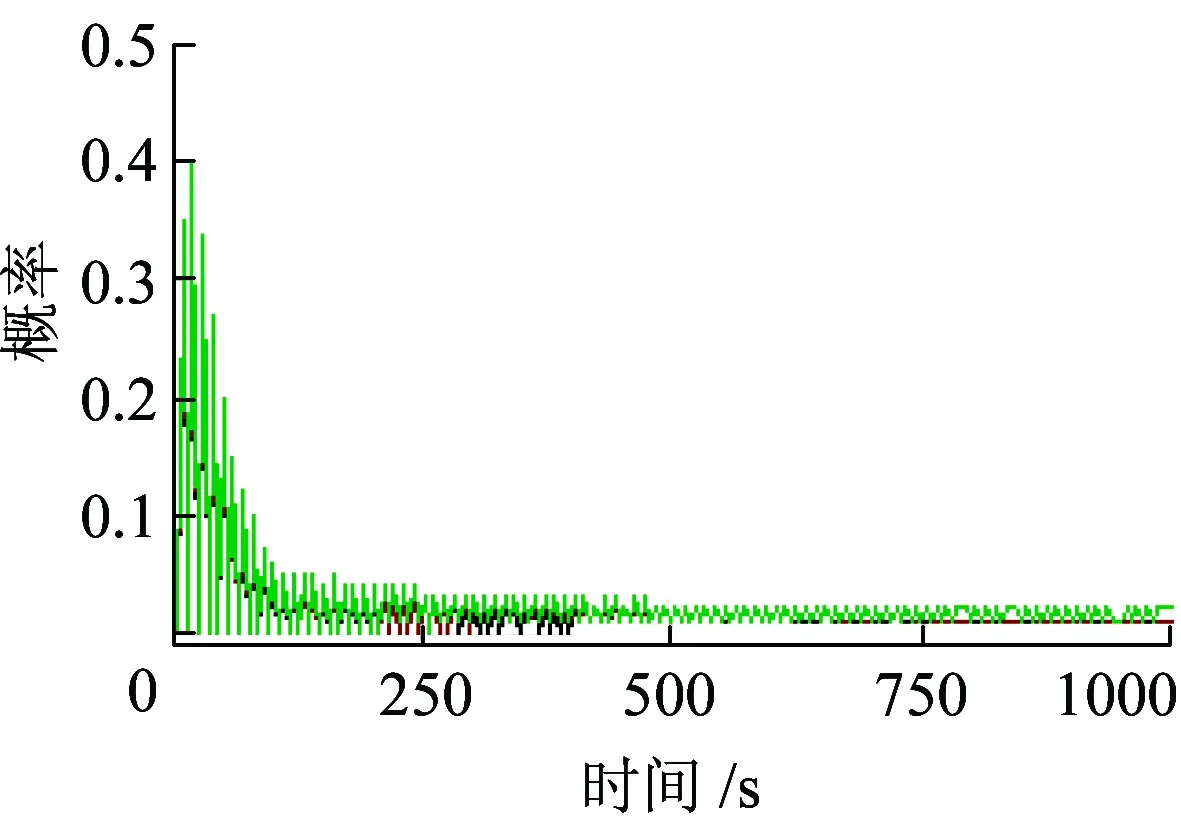
(b)下行链路图6 资源利用率

由于Transient仿真方法不计算可达图，所以像本模型中的上行链路连接丢失故障的小概率事件，采用该方法无法得到仿真结果[18，19]，因此采用Stationary Analysis的方法进行分析，通过仿真计算得出链接中断的概率R5为1×10-8/s，即0.36×10-4/h；丢包概率R4为1.651×10-5/s，即0.990 6×10-3/h，符合规范要求，并且验证了铁路时间同步网采用SPN建模的可行性。

5 结束语

本文利用随机Petri网建立铁路时间同步网模型，并对其进行形式化描述和性能计算仿真，根据随机Petri网的性能评价方法，计算出铁路时间同步网在不同同步周期下的绝对时间准确度，将计算结果与文献[5]的结果进行对比，二者结论相符，验证了模型的正确性。综合考虑建议二级节点同步周期设置为180 s，对模型客户端与服务器的正确同步概率和链路性能进行模拟仿真，结果表明铁路时间同步网客户端与服务器有较高的正确同步率，信息占用资源少，链路性能指标符合规范要求，验证了采用SPN建立铁路时间同步网模型进行分析的可行性，为铁路时间同步网制定相应性能指标规范提供依据。

参考文献：

[1]曲博.铁路时间同步网概述[J].铁路通信信号工程技术,2010,7(4):43-45.

QU Bo.Summarize of the Railway Time Synchronization Network[J].Railway Signalling & Communication Engineering,2010,7(4):43-45.

[2]王治强.铁路时间同步网的优化方案[J].铁道通信信号,2013,49(3):72-75.

WANG Zhiqiang.The Optimization Scheme of Railway Time Synchronization Network[J].Railway Signalling & Communication Engineering,2013,49(3):72-75.

[3]于佳亮,程华.基于北斗卫星同步授时的应用研究与试验[J].中国铁路,2013(4):18-21.

YU Jialiang,CHENG Hua.The Application and Experiment of the Time Synchronization Based on Beidou Satellite[J].Chinese Railways,2013(4):18-21.

[4]陆红群.关于铁路通信同步网发展的探讨[J].铁道通信信号,2012,44(8):54-58.

LU Hongqun.The Research for Development of Railway Time Synchronization Network[J].Railway Signalling & Communication Engineering,2012,48(8):54-58.

[5]施怿栋.铁路时间同步系统的测试研究[J].铁路通信信号工程技术,2012,9(1):38-40.

SHI Yidong.The Research and Test of Railway Time Synchronization System[J].Railway Signalling & Communication Engineering,2012,9(1):38-40.

[6]梦娜.京津铁路客运专线工程时间同步系统概述[J].铁路通信信号工程技术,2008,5(3):1-3.

MENG Na.An Overview of Time Synchronization System of Beijing-Tianjin Passenger Dedicated Railway Engineering[J].Railway Signalling & Communication Engineering.2008,5(3):1-3.

[7]张建东,吴勇,高晓光.基于DSPN的综合航电总线系统的性能评价[J].西北工业大学学报,2005,23(2):244-248.

ZHANG Jiandong,WU Yong,GAO Xiaoguang.Two Performance Indices Based on DSPN for Evaluating MIL-STD-1553B Bus[J].Journal of Northwestern Polytechnical University,2005,23(2):244-248.

[8]郑伟,徐洪泽.基于随机Petri网的磁悬浮列车超速防护建模及安全性分析[J].铁道学报,2009,31(4):59-64.

ZHENG Wei,XU Hongze.Modeling and Safety Analysis of Maglev Train Over-speed Protection Based on Stochastic Petri Nets[J].Journal of the China Railway Society,2009,31(4):59-64.

[9]梁楠,王海峰.基于SPN的CTCS-3级列控系统RBC实时性能分析[J].铁道学报,2011,33(2):67-71.

LIANG Nan,WANG Haifeng.Real-time Performance Analysis of RBC System for CTCS Lever 3 Using Stochastic Petri Networks[J].Journal of the China Railway Society,2011,33(2):67-71.

[10]北京全路通信信号研究设计院.铁路时间同步网技术条件[R].2012.

[11]王礼.综合调度系统的时钟同步技术研究[D].成都:西南交通大学,2008:10-45.

[12]林闯.随机Petri网和系统性能评价[M].北京:清华大学出版社,2005:19-28.

[13]王小梅,李新民.基于Petri网的网络传输协议建模与性能分析[J].计算机工程与应用,2010,46(9S):70-72.

WANG Xiaomei,LI Xinmin.Modeling and Analyzing for Network Transport Protocol Based on Petri Nets[J].Computer Engineering and Applications,2010,46 (9S):70-72.

[14]中华人民共和国信息产业部.YD/T 1171—2001 IP网络技术要求——网络性能参数与指标[S].北京：人民邮电出版社,2001.

[15]中华人民共和国铁道部.TG/DW 107—2010 铁路有线通信维护暂行规则[S].北京：中国铁道出版社,2010.

[16]赵英.基于NTP的网络时间服务测量[J].计算机工程与应用,2006 (S1):99-101.

ZAHO Ying.The Measurement of Network Time Service Based on NTP[J].Computer Engineering and Applications,2006 (S1):99-101.

[17] ZIMMERMANN A.Modeling and Evaluation of Stochastic Petri Nets with TimeNET4.1[C]//International ICST Conference on Performance Evaluation Methodologies and Tools.New York：IEEE Press,2012:54-63.

[18] ZIMMERMANN A,HOMMEL G.A Train Control System Case Sudy in Model-based Real Time System Design[J].Journal of Systems and Software,2003,7(1):41-47.

[19]陈永,王晓明,党建武.基于SPN的CTCS无线通信形式化建模与分析[J].铁道学报,2011,33(8):63-68.

CHEN Yong,WANG Xiaoming,DANG Jianwu.Formal Modeling and Analyzing of CTCS Radio Communication Based on Stochastic Petri Nets[J].Journal of the China Railway Society,2011,33(8):63-68.

[19]王锋. 铁路时间同步网可靠性分析[D]. 兰州：兰州交通大学，2015：11-30.