高速铁路区间能力部分失效情况下列车运行实时调整研究

占曙光，赵 军，彭其渊

(西南交通大学 交通运输与物流学院，四川 成都 610031)

在正常情况下，高速列车都能够按照原定的列车运行计划自动运行，不需要调度员对列车的运行进行干预。然而，由于高速铁路系统不可避免地会受到系统内部以及外部各种干扰因素的影响，从而导致列车的运行偏离原来的运行计划，需要调度员及时地对列车运行进行调整。目前我国高速铁路在非正常情况下的列车运行调整主要是以调度员的人为调整为主，系统调整为辅，在有限的时间内对高速度、高密度运行的列车进行调整对调度员而言是一项艰巨的任务。因此，为了缓解调度员的工作压力，并确保列车运行安全，研究非正常情况下的列车运行实时调整具有重要的现实意义。

近年来，干扰情况下的列车运行调整是铁路运输组织研究的热点问题之一[1]，吸引了许多国内外学者的研究兴趣。国外方面，学者们主要集中在轻微干扰情况下的列车运行调整研究，而对严重干扰情况下的列车运行调整研究尚比较缺乏。文献[2-6]对轻微干扰情况下的列车运行调整从微观层面上进行了一系列的研究，采用替代图的方法构建了列车运行调整模型，基于这一系列的研究，他们开发了ROMA系统，该系统目前主要用于实验研究，尚没有用于解决大规模的实际问题。文献[7-10]从宏观层面上对列车运行晚点管理问题进行了一系列的研究，主要是对在换乘站前行列车晚点的情况下，后行接续列车是否等待前行晚点列车问题进行研究。关于严重干扰情况下的列车运行调整，文献[11，12]从宏观层面上，基于事件-活动网络对线路区间能力全部以及部分失效情况下的列车运行调整问题分别进行了研究。

与国外相比，国内针对干扰情况下的列车运行实时调整的研究相对比较少。文献[13]对列车运行冲突进行了预测和判定，提出了基于冲突消解代价最小的列车运行调整模型。文献[14-16]对列车由于干扰偏离原运行计划情况下的列车运行调整问题进行了研究，在列车运行调整过程中主要考虑调整列车到发顺序和时刻，没有考虑是否取消列车运行。文献[17]对单线铁路在线路区间能力失效条件下的列车运行调整模型进行了研究，针对线路失效持续时间的不确定性，提出了两阶段带补偿随机期望模型，并进一步在多阶段递归决策概念模型的基础上提出了不完全连续多阶段决策模型，采用分支定界法对模型进行了求解。文献[18，19]基于事件-活动网络从宏观层面上对区间能力全部失效情况下的列车运行实时调整问题进行了研究，建立了该问题的混合整数线性规划模型，并且用中国高速铁路实际线路作为算例对模型进行了测试。

从国内外既有研究可知，高速铁路区间能力部分失效情况下的列车运行调整问题还未被广泛探讨过。国外方法探讨的高速铁路往往采用以1 h或者0.5 h为周期的运行图，且列车种类较为单一，但我国高速铁路采用非周期运行图(或者大体上可视为以天为周期的运行图)，并且一般开行多种类别的列车，因此，国外方法不适用于我国高速铁路运营的实际情况。国内未见文献针对我国高速铁路运营的特点，提出区间能力部分失效情况下的列车运行调整方法。高速铁路由于列车运行速度高，行车密度大，在双线铁路某区间一条线路出现故障导致线路通行能力失效的情况下，列车的运行调整工作比较复杂，通常需要组织双向列车在故障区间共线运行。本文在文献[11，12]的基础上，考虑到我国高速铁路调度指挥的实际需要，对区间能力部分失效情况下的列车运行调整进行研究。通过引入事件-活动网络的概念，将整个问题构建为混合整数线性规划模型，详细介绍问题目标函数和各关键约束的建模方法；设计切实案例测试所提出模型的求解能力，并与现场采用的调度策略进行比较。

1 问题描述

高速铁路在干扰情况下的列车运行调整属于复杂的组合优化问题，随着线路长度以及列车数量的增加，该问题的求解难度呈指数级增加，即该问题属于NP-Complete问题，不存在多项式算法。随着问题规模的扩大，时间或空间上无法穷举所有的可行解，需要现代优化算法探寻最优解或较优解。因此，通常都是将列车运行调整的三个阶段：运行图调整、动车组调整以及乘务调整分别进行优化，从而降低问题的求解难度。本文主要是对列车运行图进行调整，同时也通过考虑列车的均衡性兼顾考虑动车组周转。

1.1 问题定义

高速铁路一般为双线单向铁路，在正常情况下，上下行列车分别在各自的线路上按照既定的运行图运行，互不干扰，同时也不需要调度员对列车的运行进行人为调整。但是在高速铁路线路某区间能力部分失效的情况下，列车将不能按照既定的运行图运行，列车运行秩序发生紊乱。结合高速铁路的调度实际，在线路能力部分失效的情况下，调度员将组织双向列车在故障区间共线运行。在这种情况下，调度员需要充分考虑列车运行安全约束以及设备能力约束，合理安排从故障开始时刻至运营时段末双向列车通过每个区间的顺序和时刻，特别是合理安排在故障时段双向列车通过故障区间的顺序，并确定是否有列车由于线路能力下降而需要取消运行，从而减小干扰对整体列车运行的影响，提高高速铁路的服务质量。

为了更清楚地描述本文所要研究的问题，以图1所示为例进行说明。一条铁路线上有6个车站，按照下行方向分别为S1～S6，上下行各有4列车在该线路上运行，下行列车分别为G1、G3、D5和G7，上行列车分别为G2、G4、G6和D8，其中“G”表示速度相对较高的高速列车，在图1中用粗线表示；“D”表示速度相对较低的高速列车，在图1中用细线表示。假设在h1时刻，车站S3和S4之间的区间发生故障，导致该区间一条线路(如上行线路)通行能力失效，初步估计故障将持续到h2。设定在故障时段内故障区间运行的双向列车均可以追踪运行，铁路现场的列车具体组织模式将在后文进行说明。列车G1、G2、G3和G44列车从其始发站的出发时刻早于故障发生时刻h1，因此，根据规定这4列车不能取消运行，我们用实线表示这4列车的运行线；列车D5、G6、G7和D8在h1之后始发，因此，这些列车可以考虑取消运行，在图中用虚线表示它们的运行线。

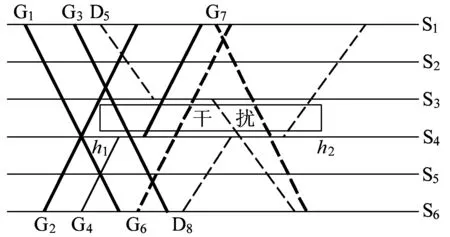
图1 区间能力部分失效情况下列车运行调整图

在车站S3和S4之间的区间发生故障的情况下，调度员首先需要合理安排故障持续时间内上下行列车通过区间(尤其是故障区间)的顺序和时刻，并确定是否有上下行列车由于线路通行能力下降而需要在靠近故障区间的车站停车等待，注意，在安排列车停站等待故障时要满足车站的能力约束。列车G1和G2由于在故障发生之前已经通过了故障区间，因此可以按计划运行图运行；G4到达故障区间时故障已经发生，且列车G3已经进入了故障区间，因此G4需要在S4站等待G3通过故障区间后才能出发；D5到达故障区间时，G4已经进入故障区间，因此D5需要在车站S3等待G4，此外，由于G6是速度相对较高的高速列车，D5可能要等到G6通过S3站后才能从S3站出发；列车D8也需要在S4站等待D5，由于G7的等级更高，D8可能还要等G7先通过故障区间。除了需决策列车的运行顺序和时刻以外，列车D5、G6、G7和D8在故障发生时还没有始发，调度员还可以根据现场列车运行情况，结合故障信息确定是否有列车需要取消运行。此外，故障时段内可能有大量的下行列车停在S3站，上行列车停在S4站，因此，故障结束后，调度员还需决策列车在其所停车站的出发顺序和时刻以及其前方途经各车站的到发顺序和时刻。本文将结合我国高速铁路的实际情况，通过建立优化模型对以上这些问题进行优化，从而为调度员的实时调度决策提供依据。

1.2 问题假设

在区间能力部分失效条件下，对列车运行进行调整是一项复杂的工作，调度员需要结合当前的列车运行状况以及故障信息在很短的时间内做出决策，同时需要考虑各种设备能力约束以及列车运行安全约束，此外，还需要遵守现场的各种调度规则。本文为了研究的方便，结合高速铁路的调度实际，对该问题所做的假设如下：

(1)为了便于调度员操作以及保证行车安全，本文假设高速铁路各车站的到发线分上下行分别使用，而且每条到发线都配有供旅客上下的站台。此外，上下行的正线与车站所有的到发线都相连。

(2)双线高速铁路每一条线路都满足组织双向行车的条件，但是在正常情况下，上下行列车分线运行，互不干扰。

(3)对于区间故障发生时已经进入故障区间的列车，需要结合现场的具体情况(故障具体的位置及故障类型等)从微观层面上进行处理，本文对该类列车的处理不做详细研究。假设进入故障区间的列车已经通过了故障地点，可以继续向前运行。

(4)由于在正常情况下高速列车基本上均能按图运行，所以本文假设所有列车在区间故障发生之前都按照运行图运行。

2 模型构建

2.1 问题抽象

为有效地解决区间能力部分失效情况下的列车运行调整这一大规模问题，本文从宏观层面上将高速铁路网络抽象为由事件和活动构成的网络N=(E，A)，其中E表示事件集合，A表示活动集合。事件e∈E表示列车在车站的到达或出发事件，因此可以将事件集合进一步划分为：到达事件集合Earr⊂E和出发事件集合Edep⊂E；活动a∈A可以进一步分为列车活动a∈Atrain和间隔活动a∈Ahead。

(1)列车活动a∈Atrain：既可以为列车运行活动a∈Arun，表示列车从一个车站出发事件到该列车在下一个车站到达事件之间的一个运行；也可以是停站活动a∈Adwell，表示列车在一个车站到达事件和在同一个车站出发事件之间的停站活动。

(2)间隔活动a∈Ahead：表示相邻的两列同向或者反向列车在区间的运行间隔或者相邻的两列同向列车在车站同一条到发线上的发到间隔。

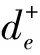
(1)

2.2 基本模型

对高速铁路在干扰情况下列车运行进行调整的主要目标为列车尽可能少地偏离原来的运行计划，体现为两个方面：一方面，尽量最小化列车在车站到发的偏离时间(晚点时间和早点时间)，相比于列车早点而言，旅客更多地关注列车的晚点，所以，可给列车晚点时间更大的惩罚系数；另一方面，尽可能最小化取消列车的数量，取消列车运行虽然能够消除晚点，但是它会对旅客的出行造成极大的影响，进而严重降低铁路的服务质量，因此，取消列车时需慎重。综合两方面考虑，本文目标为最小化加权求和列车取消和偏离计划惩罚值。基于前面定义的符号，得到不考虑能力约束的基本模型如下：

(2)

s.t.

2M1yte-M1≤xe-qe≤M1

∀e∈Ete∈T

(3)

xe≥qe∀e∈Edep

(4)

∀e∈Ete∈T

(5)

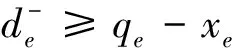
(6)

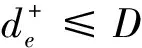
(7)

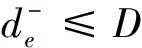
(8)

yt∈{0，1} ∀t∈T

(9)

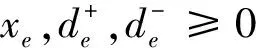
(10)

目标函数式(2)表示最小化加权求和列车取消和偏离计划惩罚值。约束条件式(3)中：te表示事件e所对应的列车，此外，约束条件式(3)实现了把取消的列车移到研究范围之后，这里表示把取消的列车移到一天之后，即取消列车的事件的实际发生时刻xe=qe+M1。将取消的列车移到研究范围之后能很好地避免被取消的列车相互间以及被取消的列车与其他列车之间的干扰。约束条件式(4)表示列车的出发时刻不能早于图定的出发时刻。约束条件式(5)表示事件e的晚点时间。约束条件式(6)表示到达事件e的早点时间，注意，结合铁路的实际情况，本文允许列车提前到达车站，但是不允许列车在车站提前发车。约束条件式(7)和式(8)分别表示列车晚点时间和到达早点时间不能超过的最大允许值。约束式(9)和式(10)限定变量的取值范围。

2.3 其他约束

列车在高速铁路线路上运行需要占用设备资源，因此，必须要满足设备的能力约束，此外，在干扰情况下列车的运行还需要遵守各种运营规则及安全约束。本文将这些约束大体上分为：单列列车运行及停站约束、相邻列车运行间隔约束、车站能力约束、列车取消约束及列车运行均衡性约束等几个方面。

(1)单列列车运行及停站约束

在线路能力部分失效情况下，虽然列车的运行受到区间故障的影响，但是对单列列车而言，其从始发站运行到终到站所经过的所有事件e和活动a的顺序都是固定的。每列车在运行过程中必须要满足其在各区间的最小运行时间约束以及在各车站的停站时间约束。具体约束条件如下：

xf-xe≥La∀a=(e，f)∈Atrain

(11)

式中：e，f分别表示同一列车先后占用同一资源的两个相邻事件；a=(e，f)表示1个列车活动，既可以是列车在区间的运行活动，也可以是列车在车站的停站活动。当a表示区间运行活动时，La表示列车在区间的最小运行时间；当a表示车站停站活动时，La表示列车在车站的最小停站时间。

(2)相邻列车运行间隔约束

为了保证行车安全，避免列车之间的冲突，相邻列车之间必须要满足运行间隔约束，主要有列车在区间的运行间隔约束和在车站同一条到发线的发到间隔约束。这里只对前者进行建模，后者将在车站能力约束部分进行分析。正常情况下，高速铁路区间运行间隔只包括相邻同向列车之间的出发间隔和到达间隔两种，但当区间能力部分失效时，故障时段内故障区间将组织双向行车，因此，不仅相邻同向列车之间需要满足出发间隔和到达间隔约束，而且相邻对向列车之间也需要满足到发间隔约束。考虑到区间能力部分失效情况下，不同等级列车间甚至同等级列车之间都可能存在越行，两列车在车站的到发顺序与原计划相比可能发生变化，本文定义一个表示事件发生先后顺序的0-1变量λef。

(12)

为了确保列车的运行安全，在任意区间任意时段内同向相邻列车之间以及故障区间故障时段内反向相邻列车之间必须要满足最小区间运行间隔约束，如式(13)、式(14)所示。

xf-xe+M2(1-λef)≥La∀a=(e，f)∈Ahead

(13)

λef+λfe=1 ∀(e，f)∈Ahead∧(f，e)∈Ahead

(14)

式中：e、f为需要占用同一列车运行资源的两个相邻事件；M2是一个足够大的正数，M2大于M1；a=(e，f)表示列车在区间的运行间隔活动，既可能是同向列车在同一站的出发间隔或者到达间隔，也可能是反向列车在同一站的到发间隔；La表示两列车在同一区间的最小运行间隔时间。式(13)中M2必须大于M1，因为基本模型将取消的列车移到了一天的最后面，只有M2大于M1才能保证取消列车与其他列车的区间运行间隔也得到满足。式(14)表示同向两列车在同一站的出发或到达以及反向两列车在同一站的到发必须满足先后顺序。式(13)和式(14)表示相邻的两列车te和tf在区间的最小运行间隔时间必须满足。

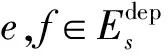
te=te′tf=tf′(s，s′)∈Seg

(15)

式(15)表示对于任意两个相邻车站之间的区间(s，s′)，若同向运行的列车te先于tf在车站s出发，则列车te也先于tf在车站s′到达，由此，不会产生一列车在区间越行另一列车的情况。

(3)车站能力约束

每一列车在每个车站的到达停车或者通过(如果按照运行图不需要停车)都需要占用车站的线路，由于资源的独占性，一条车站线路在某一段时间内只允许1列车占用，因此同一时间在每个站的列车的数量不能超过车站到发线数量。鉴于高速铁路的始发站s1和终到站sn(线路的端点站)都是大站，本文假设其到发线能力充足，只考虑中间站的能力约束，定义Sm表示线路中间站集合，s∈Sm⊂S，s≠s1，s≠sn。基于本文假设(1)，可以分别考虑车站上下行的到发线能力约束。

在车站到发线能力约束下，必须要为每一列下行(上行)到达列车分配一条下行(上行)车站线路，即需要保证每列下行列车(上行列车)到达车站时最少有一条空闲的下行(上行)线路可供使用。在每列下行列车到达每个中间站时可先统计出在该列车之前到达该车站的下行列车总数和在该列车到达之前从该车站发出的下行列车总数，进而，便可得到在该下行列车到达车站时停在车站的下行列车总数，然后把该车站下行线路数量减去停在车站的下行列车的数量就得到了车站下行方向的剩余能力，用相似的方式可以得到每个中间站在每列上行列车到达时该站的上行方向的剩余能力。

定义车站活动a=(e，f)∈Astation表示在某车站的某出发列车与后续同方向某到达列车之间的活动，Astation表示车站活动的集合，La表示从车站同一条到发线上出发的列车与后续同方向到达列车之间的最小间隔时间。对车站活动a定义0-1变量φa如下

(16)

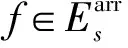
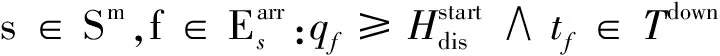
(17)

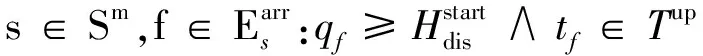
(18)

xf-xe+M2(1-φa)≥La

∀a=(e，f)∈Astation

(19)

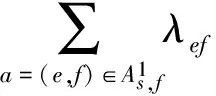
(4)列车取消约束

根据我国高速铁路运营的特点，在故障发生时已经在线路上运行的列车一般不能被取消，因为取消这样的列车将会导致大量的旅客滞留在中间车站而不能到达其目的地。但是，对于在故障发生时还没有从始发站出发的列车，调度员可以结合列车实时运行状况和现场故障信息来决定是否需要在这部分列车中选择几列列车取消运行，从而在设备能力允许的情况下，最小化故障对列车运行的影响。结合现场实际，增加列车取消约束如下

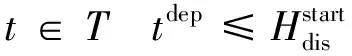
(20)

式中：tdep表示列车t在其始发站的发车时刻。

(5)列车运行均衡性约束

当故障导致线路能力部分失效时，可能有一部分列车由于线路通行能力下降而需要取消运行。在考虑取消列车运行时，与同时取消两个方向的列车相比，只取消一个方向的列车更有利于提高线路的通过能力，从而减少取消列车的数量。但是，在实际的调度指挥过程中，铁路运输部门并不偏向于采用这种只考虑取消单方向列车的方式，因为这样会造成双向运输的极大不均衡性，不仅会导致一个方向的运输质量大为降低，而且还会导致动车组不能接续的问题。考虑到动车组的周转要求，铁路运输部门更倾向于均衡地取消双方向的列车，基于此，添加列车运行均衡性约束。定义上下行列车集(p，p′)，其中p和p′分别表示上下行两个方向的同类型列车的集合，这里列车类型主要包括1类列车和2类列车，则列车运行均衡性约束可表示为

∀t∈T

(21)

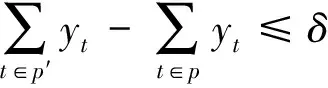
(22)

式中：δ为常量，表示上下行方向取消的同类型列车数量的允许差值，该值与始发终到站备用动车组的类型和数量有关。式(21)和式(22)表示双向同类型列车取消的数量之差不能超过允许值δ。

此外，我国高速铁路普遍配备CTCS-2或CTCS-3列控系统，采用自动闭塞，实行列车追踪运行，此种列控模式显著地提高了线路的通过能力。在高速铁路某区间能力部分失效的情况下，线路的通行能力下降，双向列车在故障区间可共线运行，此时，若组织同向列车以多列追踪的方式通过故障区间能提高故障区间线路的通过能力，从而提高整条线路的通行能力。然而，同向列车多列追踪运行的方式也可能会带来一定的问题，比如说列车到发均衡性降低，可否组织多列车在故障区间追踪运行以及组织多少列列车追踪都值得探讨。

需要说明的是，本文不直接建模列车到发的均衡性约束，但本文指出通过适当地控制事件最大允许偏离时间D的取值能够间接地确保列车到发的均衡性，原因在于计划列车运行图在铺画时已经考虑了列车到发的均衡性，通过控制参数D可限制列车运行偏离原计划的程度，从而可以间接控制列车到发的间隔，以大体上维持列车在计划运行图中的到发均衡。

(6)故障前列车运行约束

根据本文假设(4)，由于在故障发生之前难以预测故障的发生，因此，假设所有列车在故障发生之前按计划运行图运行。该假设可以用式(23)表示

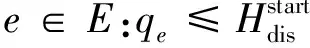
(23)

(7)有效不等式约束

显然，若1列车在某个车站的出发在另一同向列车在该车站的到达之前，则该列车在该站的到达也一定在另一列车在该站的到达之前。虽然前面的约束已隐含了这一事实，但是，加上这个有效不等式有利于加快模型的求解速度。该有效不等式可以表示为

λef≥φa′∀a=(e，f)∈Ahead

te，tf∈Tdown∨te，tf∈Tup

(24)

不等式(24)中：e，f分别表示同向列车te和tf在车站s的到达事件；e′表示列车te在车站s的出发事件。式(24)表示如果同向列车te在tf到达车站s之前从车站s出发，那么列车te也一定在列车tf之前在车站s到达。

2.4 现场调度策略建模

如前文所述，从理论上讲，在高速铁路区间由于故障导致部分能力失效的情况下，在故障区间对两个方向的列车都实行追踪运行最有利于提高线路的通过能力，从而最大程度地减小干扰对整个列车运行的影响。但是，根据我国高速铁路调度指挥的实际情况，调度员并非同等程度地对待两个方向的列车，而是给在正常线路上运行的列车更高的优先权。具体地，假如某区间的上行线路在某时刻出现故障不能行车，由我国高速铁路现场的调度策略，调度员允许下行列车(正向列车)在故障区间仍然追踪运行，而上行列车(反向列车)不能继续追踪，只能按半自动闭塞非追踪运行。显然，现场调度策略不仅会导致上下行动车组不能很好地接续，还会降低整个线路的通过能力，具体将在后文的算例分析部分得到体现。

假设故障区间为(s，s′)， 其中，s′是s的沿列车运行方向的前方车站。为了满足现场调度策略的要求，保证故障持续时间内反向列车不能继续在故障区间追踪运行，在故障区间(s，s′)内，两列相邻的反向列车t1和t2之间的最小发车间隔时间h1-2应大于等于前行列车t1在区间的运行时间h1，即后行列车t2在后方车站s的出发时刻应该不小于前行列车t1在前方车站s′的到达时刻，如图2所示，其中，左右两个子图分别表示上行和下行线路故障下故障区间两列相邻的上行和下行反向列车的运行图。

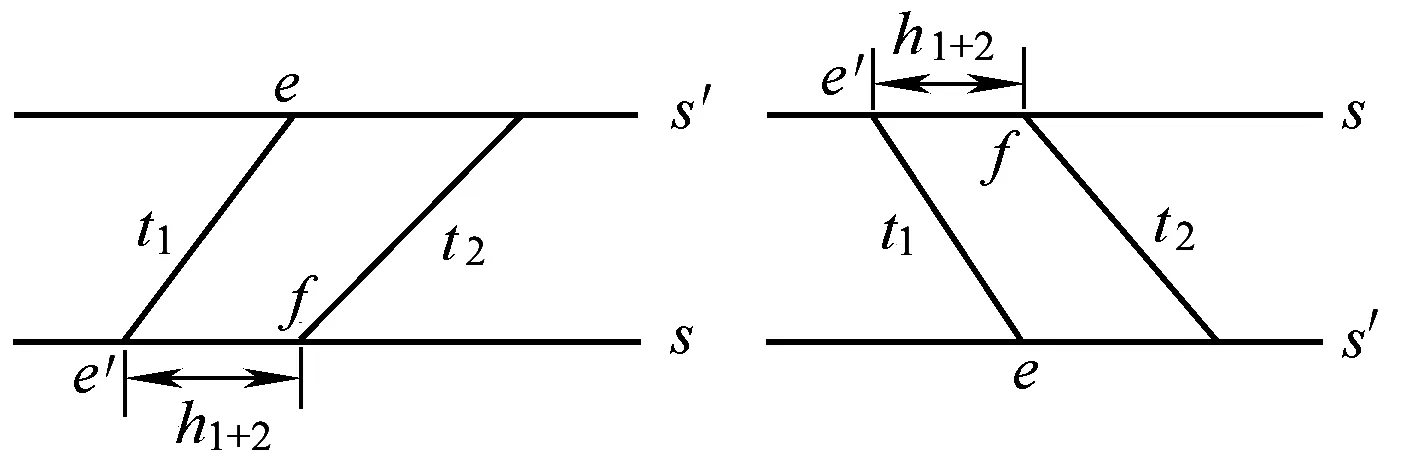
图2 现场调度策略下相邻同向列车之间的最小发车间隔时间

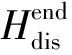
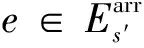
te=te′te≠tf(s，s′)∈Seg

(25)

需要说明的是，在现场调度策略下，故障区间的通过能力下降，同时也会导致原本在故障线路上运行的列车由于不能追踪运行而使晚点量增加，所以，为了保证将现场调度策略约束式(25)加入标准模型后仍能找到可行解，需适当增大事件最大允许偏离时间参数D的值，具体分析如图3所示。

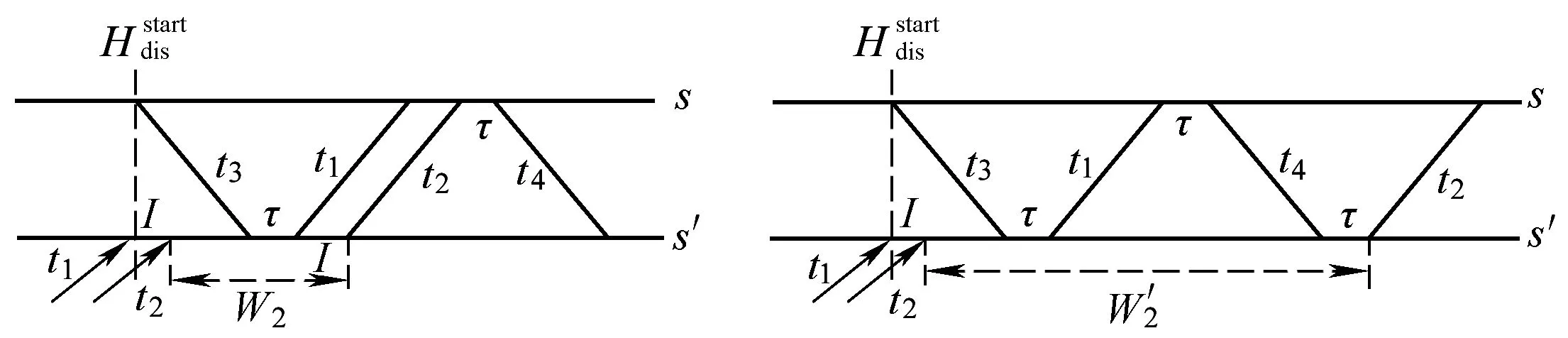
图3 不同调度策略下事件最大可能晚点时间

图3表示了区间(s，s′)下行线路能力失效情况下，基于不同的调度策略，在两列追踪运行的上行列车t1和t2中，列车t2需要在车站s′的最大可能等待时间，左子图为基于本文均衡调度策略的结果，右子图为基于现场非均衡调度策略的结果，其中，t3和t4为两列下行列车，I表示两相邻同向列车在故障区间(s，s′)的追踪间隔，τ表示两相邻反向列车在故障区间端点车站s或车站s′的到发间隔。

令hi表示列车ti在故障区间(s，s′)的最小运行时间，在本文的均衡调度策略下，列车t2需要在车站s′的等待时间W2如式(26)所示。

W2=h3+τ

(26)

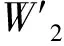
(27)

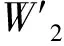
2.5 模型求解

从数学性质来看，本文构建的高速铁路区间能力部分失效情况下的列车运行调整模型属于混合整数线性规划模型(MILP)的范畴。近年来，随着数学理论和计算机技术的发展，一些商业化的优化软件功能越来越强大，能够求解数百万计变量和约束的整数线性规划问题。本文针对模型的特点，采用商业优化软件CPLEX来对模型进行求解，该软件内置的分支切割算法能够很好地用于求解本文的混合整数线性规划问题。

3 算例分析

3.1 算例描述

以京沪高速铁路为例，根据2013年调整后的列车运行图及相关数据进行算例分析。京沪高速铁路从北京南站到上海虹桥站，沿线经过23个车站(不包括天津西站)，这些车站将全线划分为22个区间。京沪高速铁路是我国的繁忙干线之一，列车开行密度大，日行车量超过100对。选择上海虹桥站和北京南站之间的42对上下行长途列车(包括从杭州等地经过上海虹桥到北京南的跨线列车)对本文提出的模型进行验证，其中，速度250 km/h的2类列车4列，速度300 km/h的1类列车80列。需要说明的是，虽然考虑的84列列车中只有4列为2类列车，大部分列车都为1类列车，但是由于同等级列车也有不同的停站模式，导致同等级列车之间也存在一定的差异，也会有列车相互越行的情况。

算例参数按以下规则进行设置。目标函数中，考虑到列车取消对旅客服务产生的影响很大，列车取消惩罚值相对比较大，同时，相比于列车出发晚点而言，旅客更在意到达晚点，因此，给到达晚点更大的惩罚值。具体地，1类列车和2类列车取消运行的惩罚值按照其票价比率分别取为5 000和3 000，同时，两类列车在车站到达晚点1 min的惩罚值分别取为5和3，出发晚点1 min的惩罚值分别取为3和2，到达早点1 min的惩罚值分别取为2和1。注意，惩罚系数的具体取值可以根据现场的经验灵活调整，本文不作重点研究，如果有需要可以对多组取值进行计算，有兴趣的读者可以参看文献[19]。事件最大允许偏离时间D取为40 min，在3.4节将针对不同的D值进行讨论。中间站可使用的到发线数量参照“京沪高速铁路动车组停车站到发线安排”取值，见表1。注意，算例只考虑42对长途列车，该部分列车的数量大概占所有列车的一半，因此，中间站的能力大概设置为其实际能力的一半。另外，在减小车站能力时，充分保证计划运行图的可行性，即如果根据计划运行图在某站某方向存在列车越行，那么该站该方向必须要保证最少有两条线路可以使用。表1中股道数所在列的第一个值表示下行方向列车可使用的股道数量，第二个值表示上行列车可以使用的车站股道数量。列车区间运行时间和车站停站时间由计划列车运行图给出，列车在区间运行时间取“京沪高铁区间运行时间标准”相应数值，见表2，列车在车站的最小停站时间取为计划运行图上的停站时间。参考文献[20]以及京沪高速铁路的实际资料，同向列车的最小出发间隔和最小到达间隔分别取为2 min和3 min，同向列车在同一到发线的最小发到间隔取为3 min，反向列车在共用故障区间线路上的最小到发间隔取为3 min。上下行同类型列车取消数量的允许差值δ取为1，M1取为1 440，M2取为2 880。计划列车运行图如图4所示。

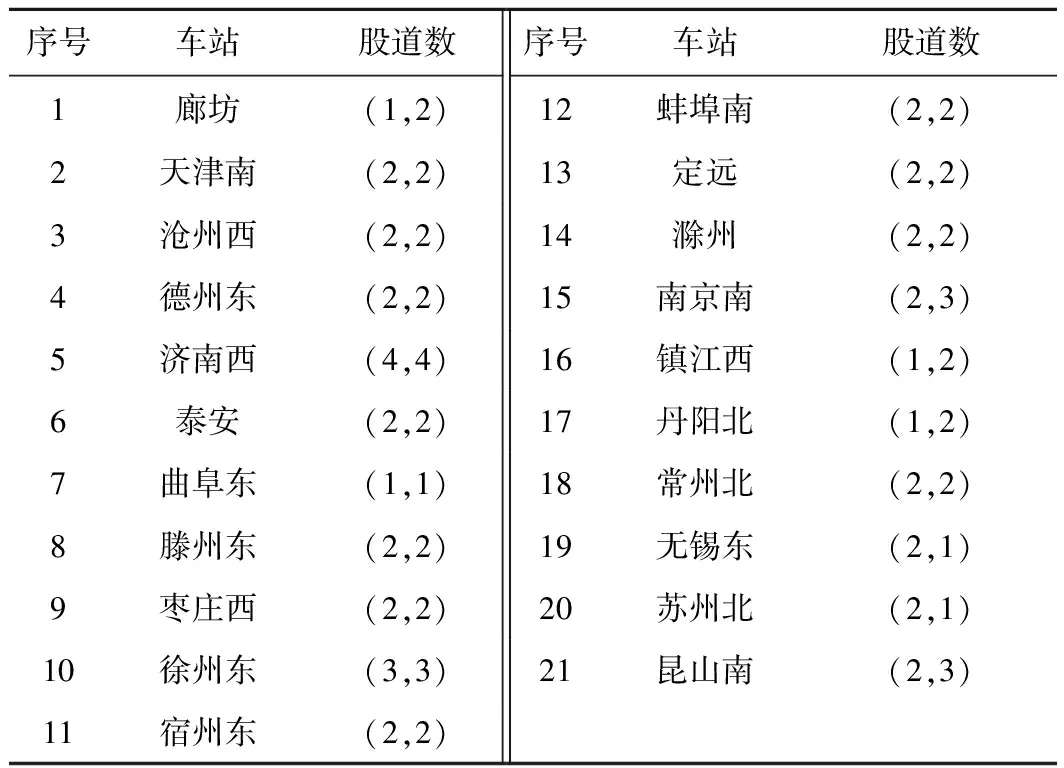
表1 京沪高铁中间站股道数量

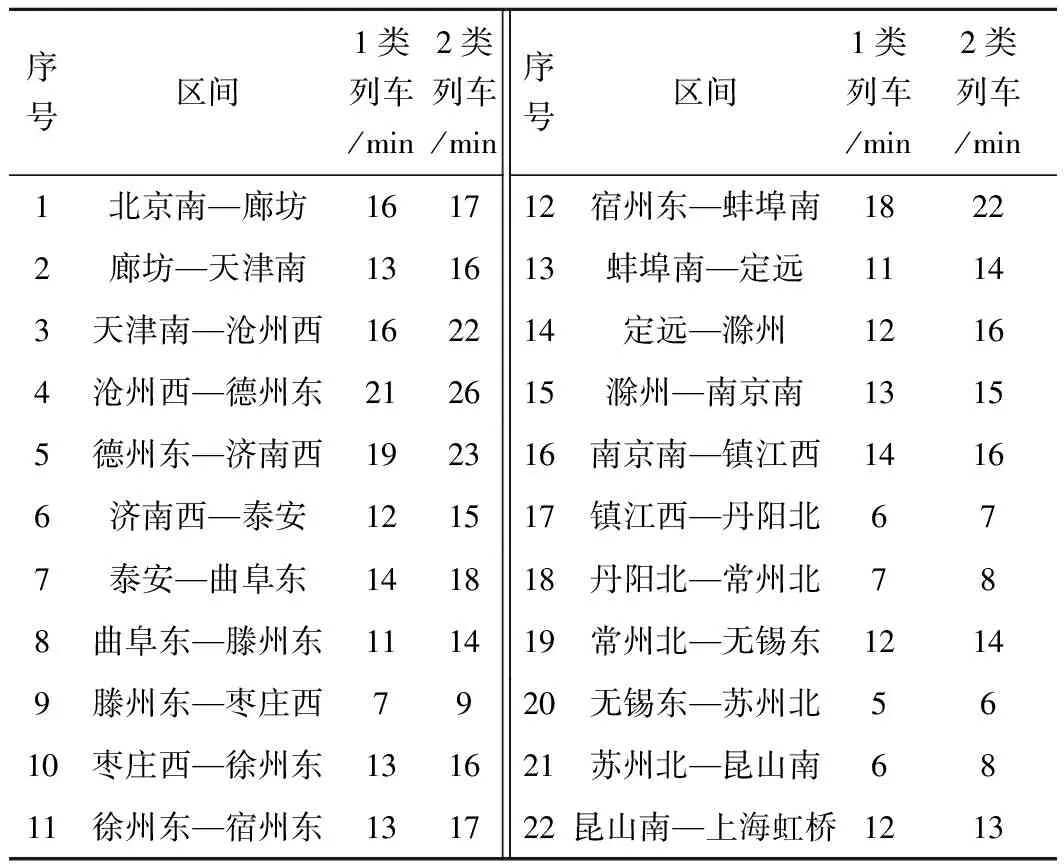
表2 区间最小运行时间

注：同类列车在同一区间上下行最小运行时间相同。

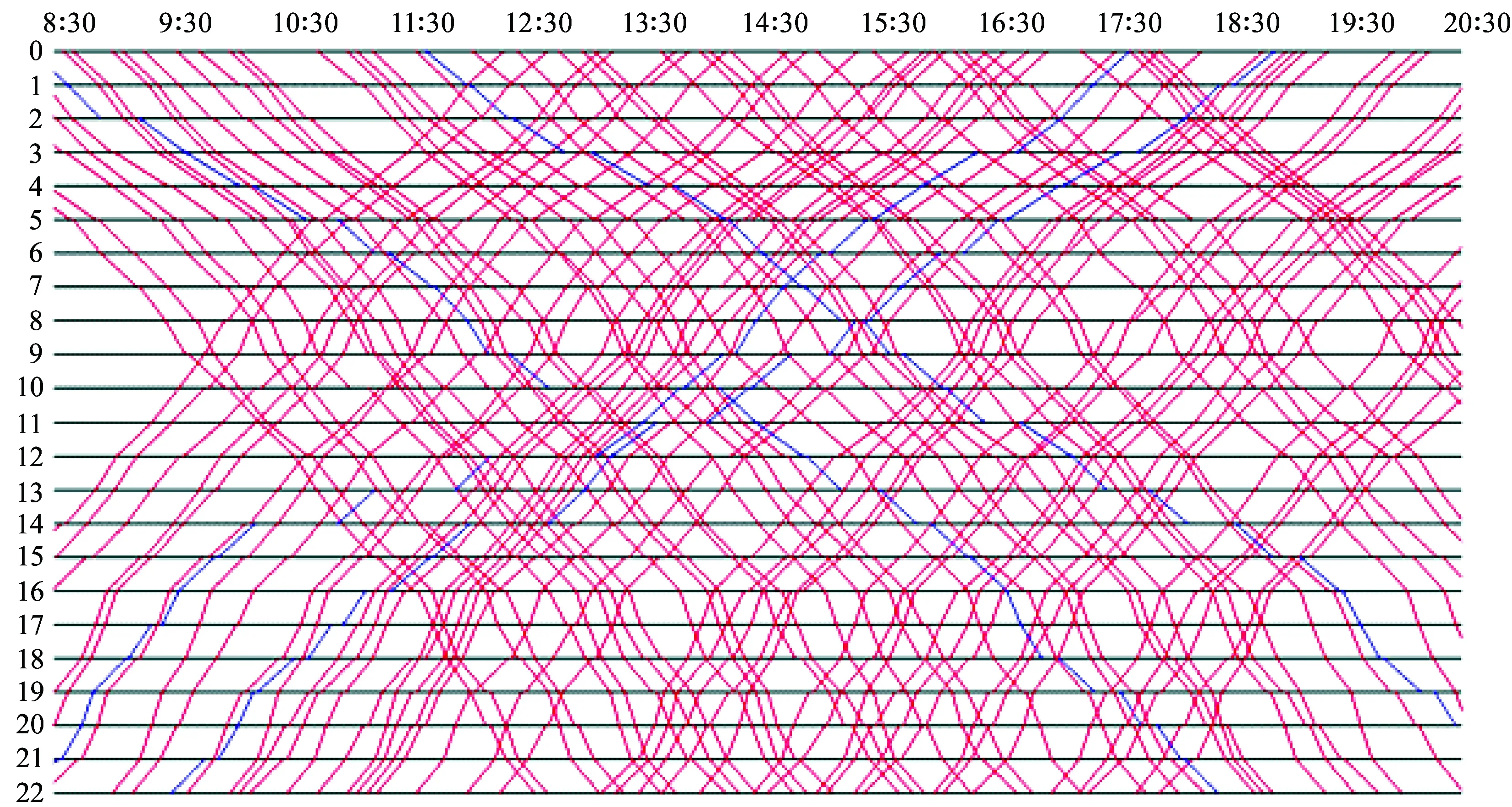
注：红色线表示1类列车，蓝色线表示2类列车；车站沿下行方向从0开始依次编号。图4 北京南和上海虹桥之间42对长途列车计划运行图

结合京沪高速铁路的基本情况，通过调整故障发生的时间和地点设计3种故障场景，每种故障场景下再通过调整故障持续时间分别设置3种干扰情景。3种故障场景及其各自对应的3种干扰情景具体设置如下：

故障场景1：在10：30，由于某种原因导致京沪高铁德州东站—济南西站之间的上行线路出现故障，区间上行通行能力丧失，调整故障持续时间设置3种干扰情景，其故障持续时间分别为60 min、90 min和120 min。

故障场景2：在13：30，徐州东站—宿州东站之间的线路区间下行线路出现故障，导致该区间下行线路通行能力失效60 min、90 min和120 min。

故障场景3：在17：30，南京南站—镇江西站之间的线路区间由于故障导致该区间上行线路能力失效60 min、90 min和120 min。

为了便于描述不同故障场景下的干扰情景，定义1个三元组(a，b，c)，其中，a表示故障发生时刻，b表示故障所在区间，c表示故障持续时间。3种故障场景下的9种干扰情景用所对应的三元组进行表示的结果见表3。

3.2 计算结果

在CPU为Inter(R)Core(TM)i7-4600U 2.1 GHZ，内存为8 GB，操作系统为Windows8.1的64位电脑上采用IBM ILOG OPL(Optimization Programming Language)编程，并调用CPLEX 12.6对所提出的模型进行求解。在CPLEX中，相关参数设置为其默认值，求解算法选择内置的将分支定界法和割平面法相结合的分支切割算法。鉴于列车运行调整的实时性要求，限制程序的最长运行时间为5 min。3.1节中3种故障场景下9种干扰情景的列车运行调整计算结果见表4。需要说明的是，通过初步计算测试发现，在故障结束较长时间之后列车基本上能够恢复计划图运行，因此，为了减小干扰对列车正常运行的影响范围，测试算例中假定故障结束5 h后列车恢复正常运行。

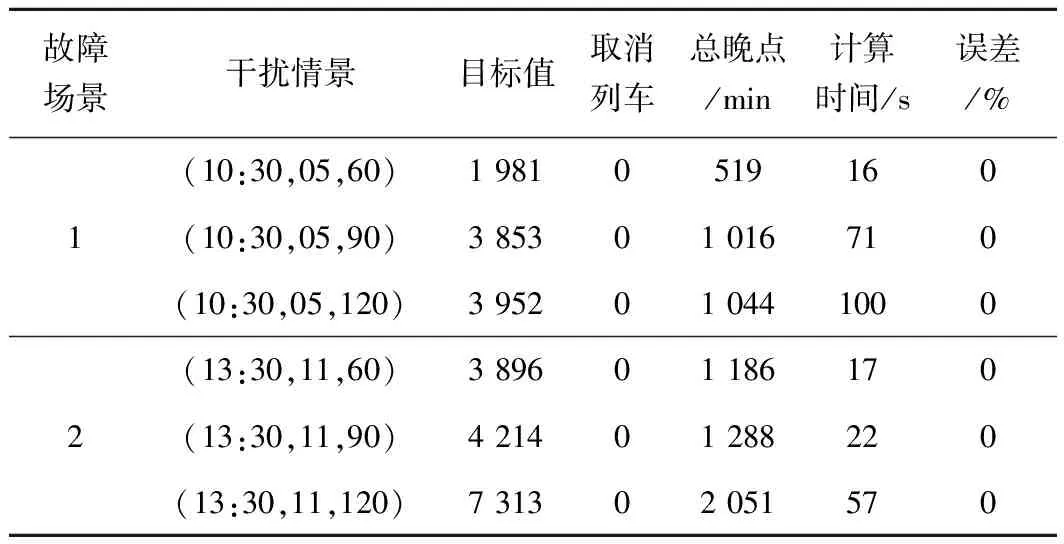
表4 不同干扰情境下的列车运行调整结果

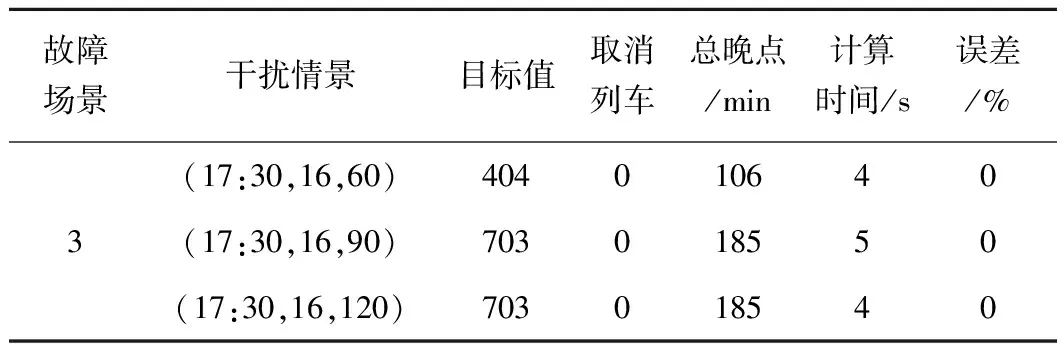
表4续

从表4可以看出，不同的故障场景和干扰情景对列车运行的影响各不相同。接近中午时刻(13：30)发生在线路中部的干扰对列车运行的影响最为严重，如故障场景2中的干扰对列车运行的影响大于故障场景1、3。同一故障场景下，通常干扰持续时间越长，对列车运行的影响越大。但是，需指出的是，故障场景3中故障持续90 min和120 min产生的影响是一样的，原因在于故障发生的比较晚，此时大多数列车都已经通过了故障区间，受影响的列车很少。关于计算时间，本文模型对所有的干扰情景都可在100 s的时间内快速获得最优的列车运行调整方案，可见该模型能较好地满足现场调度员实时决策的需要。

接下来分析基于本文模型均衡调度策略的质量，限于篇幅，只以干扰情景(13：30，11，120)为例，其基于本文模型的列车运行调整图如图5所示。如前文所述，理论研究成果已表明，相比于非追踪运行，单线铁路采用追踪运行能力更大，所以对于区间能力部分失效情况，最佳的调度策略应是对故障区间在故障时段内实行列车追踪运行，以最小化列车运行受干扰的影响。图5显示了对于干扰情景(13：30，11，120)，本文模型首先调度1列上行列车运行，然后是3列下行列车追踪，接着是2列上行列车追踪，最后是3列下行列车追踪，也就是说，间隔调度两个方向的列车追踪运行，体现了本文模型可获得最佳的调度策略。

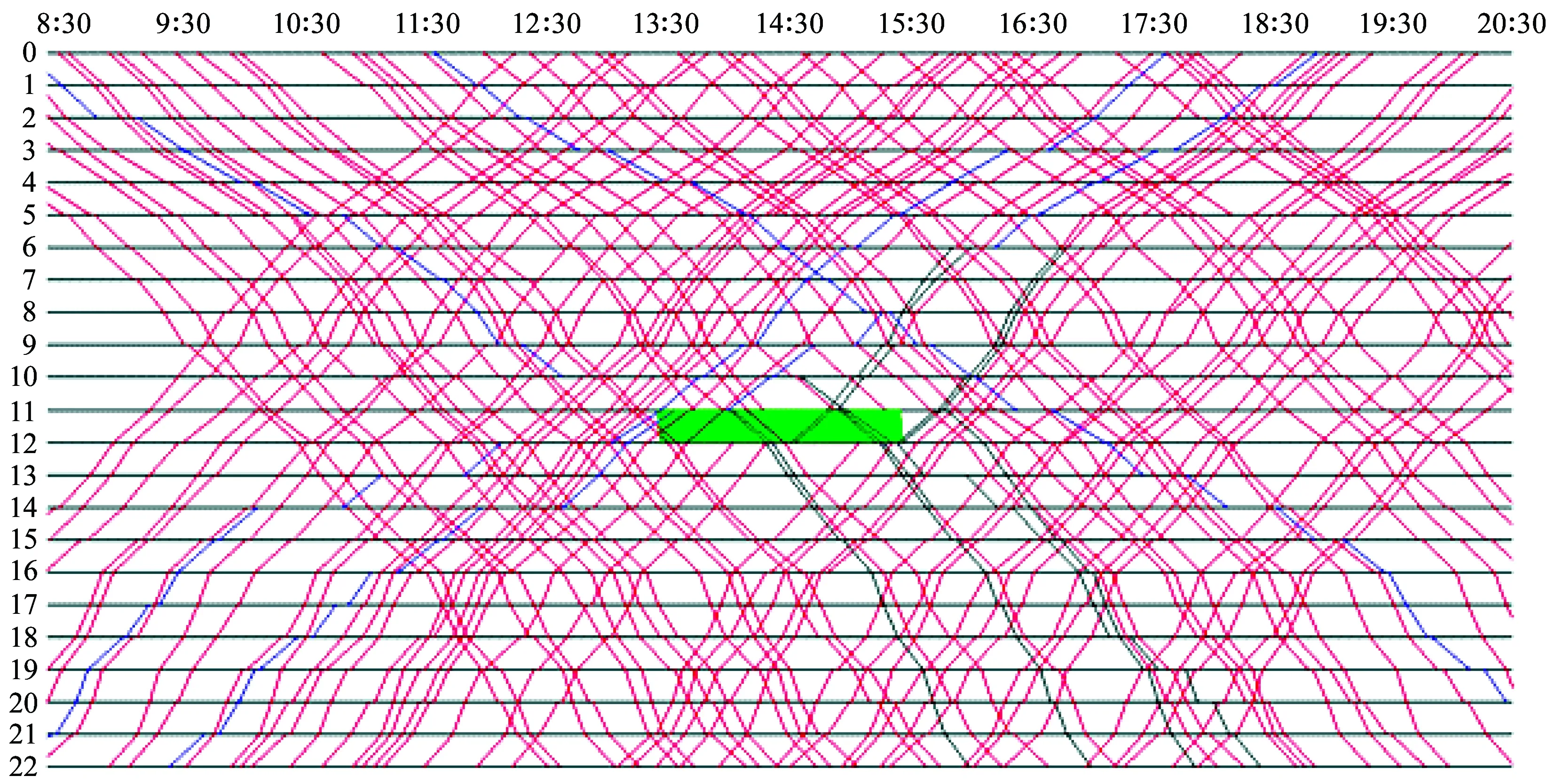
注：绿色块表示故障，红色和蓝色线分别表示1和2类列车的运行线，黑色线表示列车运行线偏离了原始运行计划。

图5 干扰情景(13：30，11，120)的列车运行调整图

3.3 与现场调度策略的比较

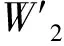
比较表4和表5可发现，在相同的故障场景下，相比于目前我国高速铁路普遍采用的只允许故障区间故障时段内单向追踪的非均衡调度策略，本文提出的允许故障区间故障时段内双向追踪的均衡调度策略可获得更好的列车运行调整结果。当故障发生在接近中午并处于线路中部时，与现场的非均衡调度策略相比，本文的均衡调度策略能使列车由于干扰而偏离原计划的惩罚值减小超过一半，更为直观地比较如图6所示。由此可见，当高速铁路区间线路部分失效时，调度员应该在条件允许的情况下采用均衡调度策略，以在尽可能保证列车运行均衡性的前提下最大程度地减小故障对列车运行的影响。需要说明的是，高速铁路的信号设备具备组织单条正线双向追踪运行的条件是实施均衡调度策略的前提。

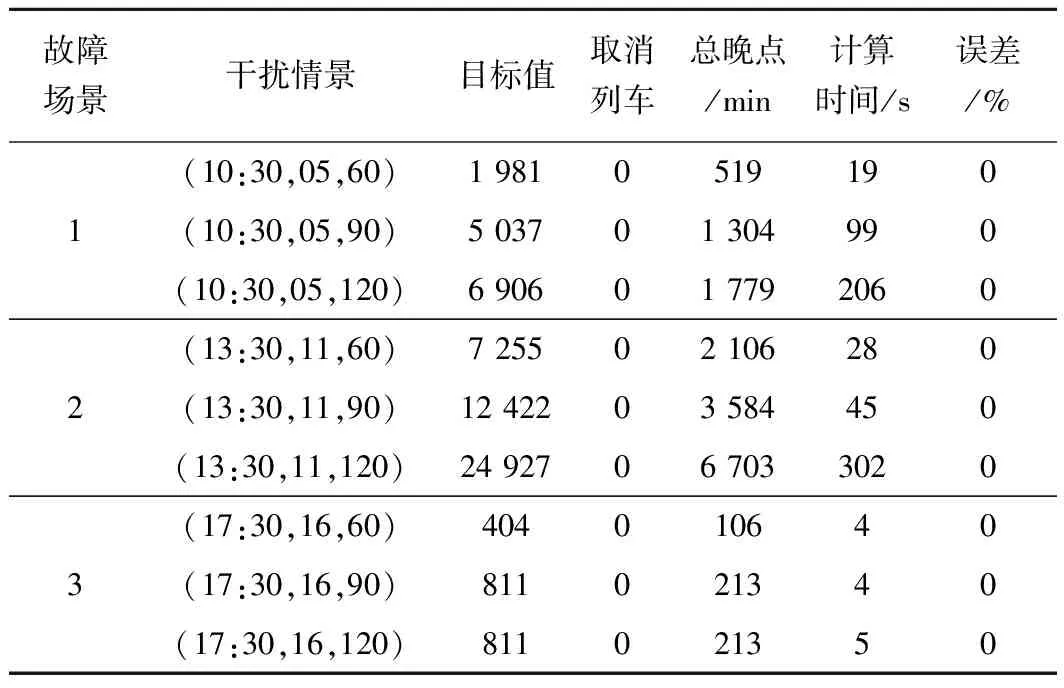
表5 基于现场调度策略的列车运行调整结果

为了更为形象地显示本文均衡调度策略与现场非均衡调度策略的区别， 干扰情景(13：30，11，120)基于现场非均衡调度策略的列车运行调整图如图7所示。从图7可以看出，由于区间11下行线路故障，在现场调度策略下，只有上行列车可以追踪，而下行列车由于线路故障不能追踪，最终故障区间故障时段内在正常的上行线路只放行了7列列车(上行3列，下行4列)。对于同样的干扰情景，本文调度策略可放行9列列车。注意，这里只统计故障发生之后才进入故障区间的列车，因为由本文假设(4)，在故障发生时已经进入故障区间的列车无论在哪种调度策略下都将按计划运行图运行。显然，在信号设备允许的情况下，本文的均衡调度策略明显优于现场的非均衡调度策略。根据现场调研了解到，大部分高铁的沿线技术设备都满足组织双向列车追踪运行的条件，但是，由于目前的调度系统连锁设备不满足组织反向列车追踪运行的条件，因此，高速铁路非正常情况下行车组织中规定：在区间一条线路封锁的情况下，只允许正向列车追踪运行，反向列车只能按站间控制的方式来组织列车运行。

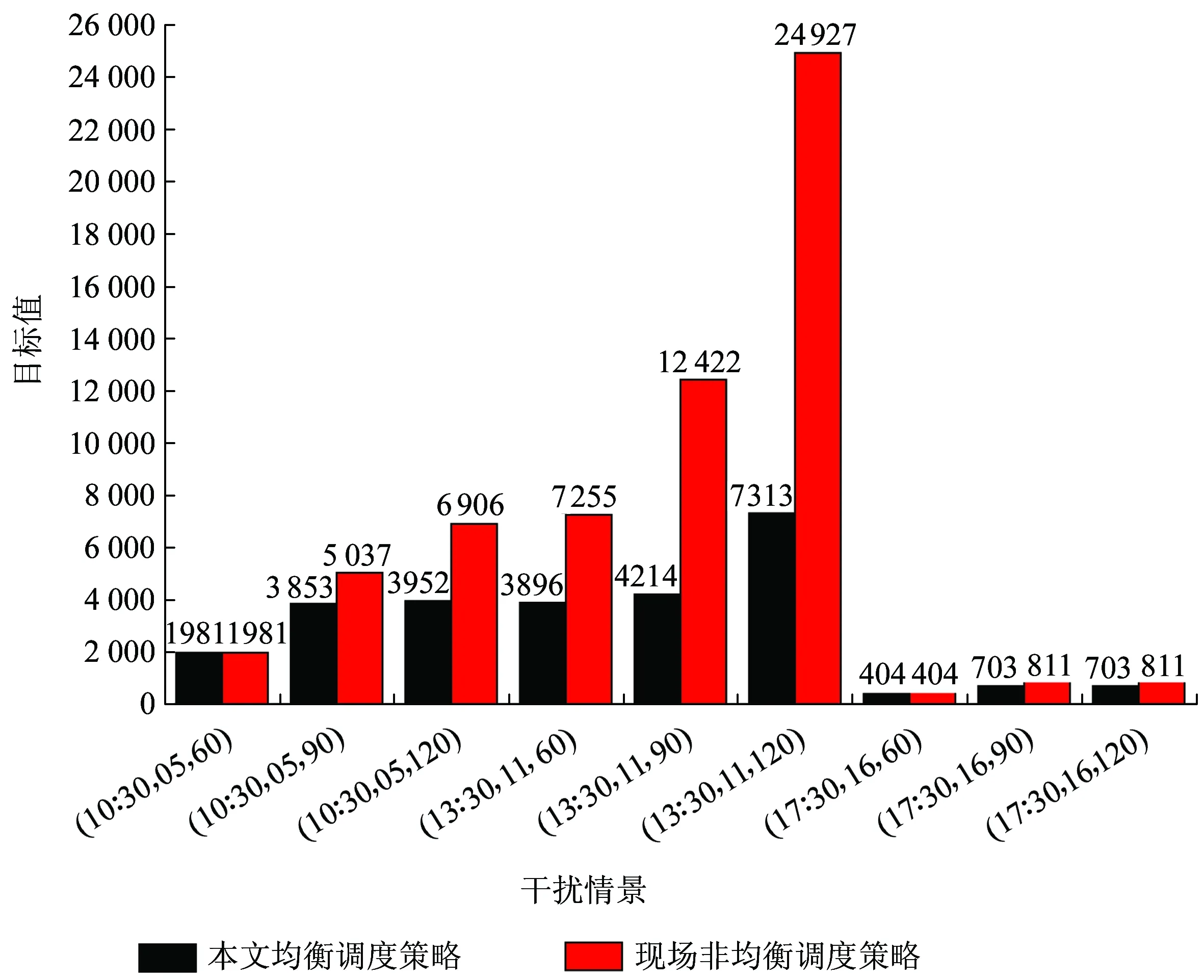
图6 两种调度策略下的目标函数值

3.4 事件最大允许偏离时间灵敏度分析

前文已述，在所提出的模型中，事件最大允许偏离时间D是很重要的参数，其值需合理设置。若参数D设置的相对比较小，则在故障区间故障时段内，同向追踪运行的列车数量将减少，以至于降低故障区间的通过能力，并恶化整个问题的目标函数。更为严重的是，若参数D设置的太小，因为本文假设在故障发生前已经出发的列车不能取消运行，则有可能会导致整个问题无可行解。当然，小的参数D可以获得列车到发相对均衡的列车运行调整方案。反之，若参数D设置的相对比较大，则在故障区间的故障时段内，同向列车将尽可能多地追踪运行，以提高故障区间的通过能力，并最小化整个问题的目标函数。但是，过大的参数D也有可能影响计划运行图中列车到发的均衡性，导致调整图中列车运行极为不均衡，这同样是需要避免的。

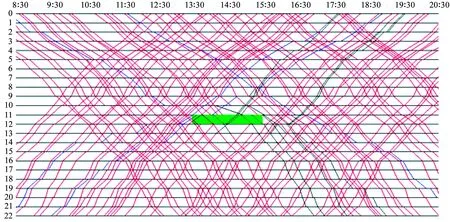
图7 干扰情景(13：30，11，120)基于现场调度策略的列车运行调整图

本节分别以故障场景1和2中的3个干扰情景为例，采用灵敏度分析方法评估参数D对整个问题目标函数的影响。对于故障场景1，通过计算测试发现，当D值小于24 min时，会导致原问题无解，所以D值最小取为24 min，逐步增加到30 min，步长为1 min，灵敏度分析结果如图8所示。同理，针对故障场景2，从使原模型有解的最小D值37 min依次增加到41 min，所得的灵敏度分析结果如图9所示。值得说明的是，由于故障场景3下，列车受故障影响很小，所以D值对最终结果的影响不大，不对其作灵敏度分析。

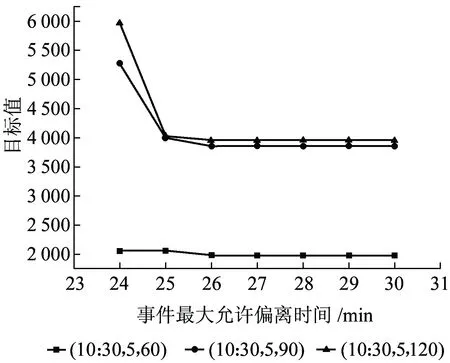
图8 故障场景1下事件最大允许偏离时间灵敏度分析

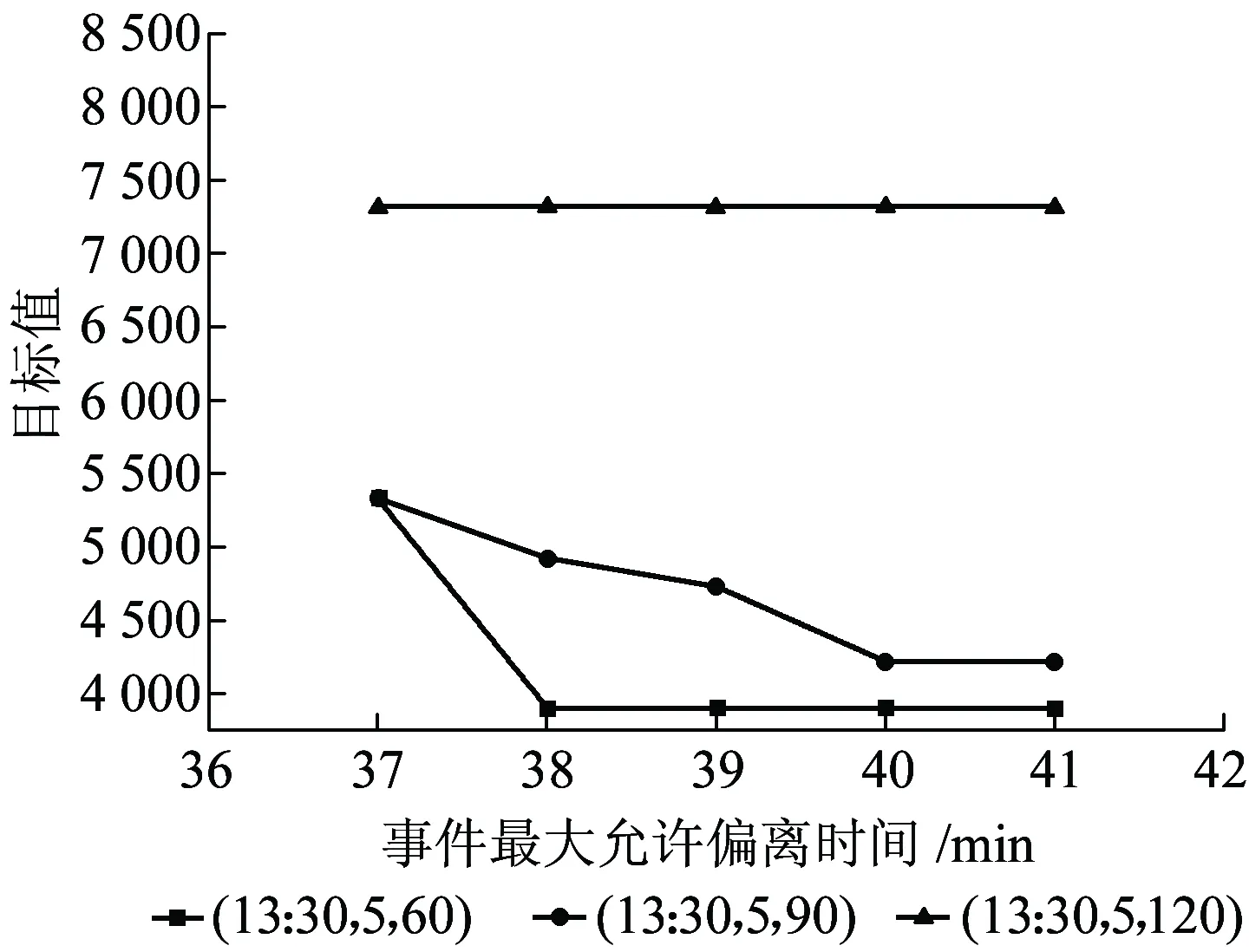
图9 故障场景2下事件最大允许偏离时间灵敏度分析

从图8和图9可以看出，当D值增加时，目标函数值下降，体现了D值与目标函数值的反相关关系。但是，当D值增加到一定数值之后，其对计算结果的影响已不明显。对于故障场景1，当D值大于等于26 min时，其对目标函数值的影响基本保持不变，意味着场景1中3种干扰情景的D值都可设置为26 min，以最大程度地维持列车到发的均衡性。类似地，对于故障场景2，为尽量避免影响列车在计划运行图中的均衡性，其3种干扰情景的D值都可取为40 min。基于灵敏度分析结果，调度员可更为清楚地认识参数D的作用，从而更为有效地权衡列车运行调整的质量与列车到发的均衡性。

4 结束语

本文引入事件和活动的概念将我国高速铁路网络从宏观层面上抽象为由事件和活动构成的网络，基于此对高速铁路区间能力部分失效情况下列车运行实时调整问题进行了阐述。在考虑列车运行安全约束以及设备能力约束的基础上，建立了基于列车均衡运行的高速铁路区间能力部分失效情况下列车运行实时调整的MILP模型。结合我国高速铁路列车运行调整的实际情况，模拟了在现场调度员普遍采用的非均衡调度策略。

以京沪高速铁路全天上下行42对长途列车的实际数据为依据，考虑到高速铁路线路故障的随机性和不确定性，假设了三种不同故障场景，并又各自分别设置了三种不同干扰情景。采用本文模型对各种干扰情景下的列车运行实时调整方案进行了计算。同时，通过与目前我国高铁调度员通常采用的只允许单向列车追踪运行的非均衡调度策略进行了对比，突出了本文的均衡调度策略在减小故障对整个列车运行影响方面的优越性。

区间能力部分失效情况下的列车运行调整是大规模组合优化问题，整个问题的求解非常困难。为了满足实时的需要，本文只针对列车运行图调整从宏观层面上进行了研究，通过建模列车运行的均衡性，间接地考虑了动车组的周转。算例中也仅考虑了长途列车，还需要对所有列车包括短途和跨线列车进行研究。此外，本文是基于假设故障持续时间已知的情况下，对列车运行调整问题进行了研究，考虑到故障的不确定性，将本文模型扩展到处理故障持续时间不确定情况下的列车运行调整问题也是下一步研究的重点。

参考文献：

[1]CACCHIANI V,HUISMAN D,KIDD M P,et al.Anoverview of Recovery Models and Algorithms for Real-time Railway Rescheduling[J].Transportation Research Part B:Methodological,2014,63(5):15-37.

[2]D’Ariano A,PRANZO M,HANSEN I A.Conflict Resolution and Train Speed Coordination for Solving Real-time Timetable Perturbations[J].IEEE Transactions on Intelligent Transportation Systems,2007,8(2):208-222.

[3]CORMAN F,D’Ariano A,PACCIARELLI D,et al.Bi-objective Conflict Detection and Resolution in Railway Traffic Management[J].Transportation Research Part C:Emerging Technologies,2012,20(1):79-94.

[4]CORMAN F,D’Ariano A,PACCIARELLI D,et al.Centralized Versus Distributed Systems to Reschedule Trains in Two Dispatching Areas[J].Public Transport,2010,2(3):219-247.

[5]CORMAN F,D’Ariano A,PACCIARELLI D,et al.A Tabu Search Algorithm for Rerouting Trains During Rail Operations[J].Transportation Research Part B:Methodological,2010,44(1):175-192.

[6]CORMAN F,D’Ariano A,HANSEN I A,et al.Optimal Multi-class Rescheduling of Railway Traffic[J].Journal of Rail Transport Planning & Management,2011,1(1):14-24.

[7]GINKEL A,SCHÖBELA.To Wait or Not to Wait?The Bicriteria Delay Management Problem in Public Transportation[J].Transportation Science,2007,41(4):527-538.

[8]SCHACHTEBECK M,SCHÖBELA.To Wait or Not to Wait-And Who Goes First?Delay Management with Priority Decisions[J].Transportation Science,2010,44(3):307-321.

[9]DOLLEVOET T,HUISMAN D,SCHMIDT M,et al.Delay Management with Rerouting of Passengers[J].Transportation Science,2012,46(1):74-89.

[10]DOLLEVOET T,HUISMAN D,KROON L G,et al.Delay Management Including Capacities of Stations[J].Transportation Science,2014,46(1):74-89.

[11]LOUWERSE I,HUISMAN D.Adjusting a Railway Timetable in Case of Partial or Complete Blockades[J].European Journal of Operational Research,2013,235(3):583-593.

[12]VEELENTURF L P,KIDD M P,CACCHIANI V,et al.A Railway Timetable Rescheduling Approachfor Handling Large Scale Disruptions[J].Transportation Science, 2016,50(3):841-862.

[13]文超.高速铁路列车运行冲突管理研究[D].成都：西南交通大学,2011:12-16.

[14]MENG L Y，ZHOU X S.Robust Single-track Train Dispatching Model Under a Dynamic and Stochastic Environment:A scenario-based Rolling Horizon Solution Approach[J].Transportation Research Part B:Methodological,2011,45(7):1 080-1 102.

[15]YANG L X,ZHOU X S,GAO Z Y.Rescheduling Trains with Scenario-based Fuzzy Recovery Time Resentation on Two-way Double-track Railways[J].Soft Computing,2013,17(4):605-616.

[16]YANG L X,ZHOU X S,GAO Z Y.Credibility-based Rescheduling Model in a Double-track Railway Network:a Fuzzy Reliable Optimization Approach[J].Omega,2014,48(10):75-93.

[17]孟令云，杨肇夏，李海鹰.单线铁路区间能力失效条件下列车运行调整模型[J].系统工程理论与实践，2012，32(4)：885-894.

MENG Lingyun,YANG Zhaoxia,LI Haiying.Train Dispatching Models Under Field Capacity Breakdowns on Single-track Railway Lines[J].Systems Engineering-Theory&Practice,202,32(4)：885-894.

[18]占曙光，赵军，彭其渊，等.高速铁路区间能力全失效条件下列车运行实时调整研究[J].铁道学报，2015，37(11):1-9.

ZHAN Shuguang,ZHAO Jun,PENG Qiyuan,et al.Real-time Train Rescheduling on High-speed Railway under Complete Segment Blockages[J].Journal of the China Railway Society,2015，37(11):1-9.

[19]ZHAN S G,KROON L G,VEELENTURF LP,et al.Real-time High-speed Train Rescheduling in Case of a Complete Blockage[J].Transportation Research Part B:Methodological,2015,78(8):182-201.

[20]史峰，魏堂建，周文梁，等.考虑动车组周转和到发线运用的高速铁路列车运行图优化方法[J].中国铁道科学，2012,33(2):107-114.

SHI Feng,WEI Tangjian,ZHOU Wenliang,et al.Optimization Method for Train Diagram of High-speed Railway consider the turnover of Multiple Units and the Utilization of Arrival-Departure Tracks[J].China Railway Science,2012,33(2):107-114.