钢筋混凝土梁爆损后生存能力计算与分析

彭　芸　富　裕

(西南科技大学土木工程与建筑学院　四川绵阳　621010)



钢筋混凝土梁爆损后生存能力计算与分析

彭芸富裕

(西南科技大学土木工程与建筑学院四川绵阳621010)

摘要：为了评估钢筋混凝土梁在爆炸受损后的生存能力，以确定其继续服役的可能性，控制修复加固的工程量和造价，利用有限元软件ANSYS/LS-DYNA数值模拟分析了在不同炸药量、炸点高度和炸点位置条件下钢筋混凝土梁在爆炸荷载作用下的破坏模式和损毁形态，计算了其爆后剩余承载力和损伤度，并据此评估了其生存能力。结果表明，以受弯承载力的损失程度作为损伤指标来进行钢筋混凝土梁爆后生存能力的评估是可行的，同时可为地面建筑结构抗爆防护研究与结构设计提供参考。

关键词：钢筋混凝土梁爆后剩余承载力爆后生存能力数值模拟

恐怖爆炸袭击以及生产生活中意外爆炸事故的频繁发生，造成了大量的人员伤亡和财产损失，地面建筑结构在这些突发灾难中损伤程度不一，其灾后处理措施也会不同。钢筋混凝土框架结构是最普遍的建筑结构形式，应用于各种建筑工程或防护工事结构中。对于经受爆炸荷载作用的地面建筑结构，根据钢筋混凝土关键构件或结构的损伤程度，评估其剩余承载力、生存能力及其继续服役的可能性，为建筑结构灾后修复工程提供理论支持，是工程实践中亟待解决的重要问题，也可为建筑结构抗爆防护研究与结构设计提供参考。目前，国内外研究者[1-11]主要着眼于爆炸荷载作用下钢筋混凝土关键构件(梁、柱、楼板)和结构的动态响应、破坏形态和连续倒塌的研究，而对于爆后损伤构件或结构的损伤评估和生存能力的研究却关注不多[12-14]。本文借助ANSYS/LS-DYNA有限元分析软件，在不同炸药量、炸点高度和炸点位置条件下，对钢筋混凝土梁在爆炸荷载作用下的破坏模式和损毁形态进行了研究，并依据规范对钢筋混凝土梁的爆后剩余承载力进行了分析，根据其损伤度D值对其生存能力进行了评估，以期利用D值来确定该构件的生存能力以及后续的处理措施，从而控制灾后修复加固的工程量和造价。

1爆后生存能力评估方法

爆后生存能力是指构件或结构在经受爆炸荷载作用后还能维持安全且可再用状态的能力。文献[13-14]指出，目前常用跨中最大挠度作为钢筋混凝土关键构件(梁、柱、楼板)的损伤指标，但对于爆炸荷载作用下可能出现的剪切破坏、弯剪破坏以及冲剪破坏，跨中最大挠度并不适用。受弯承载力是受弯构件的基本设计参数，因此受弯承载力的损失程度直接和钢筋混凝土梁的整体性能相关，作为损伤指标，能适用于各种破坏模式，包括弯曲破坏、剪切破坏、弯剪破坏以及冲剪破坏或局部震塌破坏。

本文定义梁的损伤度D来描述构件的爆后生存能力，表达式为：

(1)

其中，Rf为梁爆后剩余承载力，S为梁爆前设计承载力。综合文献[13-14]和行业标准文献[15-16]，各个损伤等级的准则为：D=0～0.05为无损伤，不必处理，可以继续使用；D=0.05～0.2为轻度损伤，可经修复后继续使用；D=0.2～0.5为中度损伤，应采取加固措施后再使用；D=0.5～1为严重损伤或失效，需要拆除重建。

钢筋混凝土梁的受弯承载力借用《金属材料弯曲试验方法》[17]中抗弯强度的测定方法来获得。建立钢筋混凝土梁三点弯曲试验计算模型，根据《混凝土结构设计规范》[18]第3.5.3条中规定受弯构件的挠度限值为L/300(L为梁净跨)，若超过该规定限值，则认为该梁破坏。由此，当跨中挠度达到L/300时，对应的跨中竖向荷载即作为梁的受弯承载力。其中梁爆后计算模型仅保留梁在爆炸荷载作用下产生的变形和位移。

2计算模型

2.1构件尺寸

本文钢筋混凝土梁截面尺寸为250mm×550mm，梁净跨为6.65m。梁上部有2根直径20mm通长钢筋，左右端支座各配筋8根直径20mm的钢筋(分两排布置)，梁下部直径20mm和25mm的钢筋各两根。梁腰部配有4根直径12mm抗扭钢筋。箍筋为两肢箍，直径10mm，间距100mm。

2.2几何模型

本文爆炸计算模型由炸药、混凝土、钢筋和空气4部分组成。其中混凝土和钢筋采用拉格朗日网格建模，炸药和空气采用欧拉网格建模，单元使用多物质ALE算法。假设炸药是条形装药，中心点起爆。本文计算分别考虑3种炸药量W(1.63 ,5.5,13kg)，5种炸点高度H(0m/接触，0.5,1,2，4m)，3种炸点位置X(L/2,L/5,L/15，L为梁净跨)。计算时间20ms，采用mm-g-ms单位制。钢筋混凝土梁采用分离式建模，如图1所示。

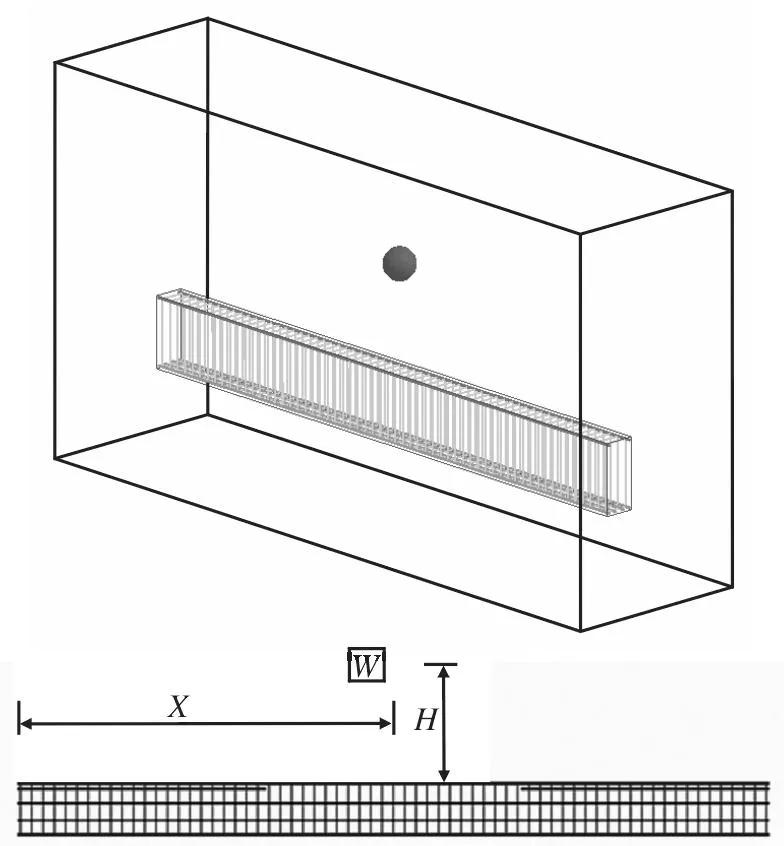
图1　钢筋混凝土梁的计算模型

2.3材料模型

梁钢筋采用*MAT_PLASTIC_KINEMATIC模型，参数[6,19]见表1。混凝土采用*MAT_CONCRETE_DAMAGE_REL3模型(简称K&C)，该模型是美国Karagozian & Case公司研发的混凝土材料模型，能够较真实地模拟混凝土在高速撞击、爆炸等极限荷载作用下的动力反应，且模型参数简单。本文混凝土C40，材料参数[18]见表2，并添加失效判据*MAT_ADD_EROSION，当拉应力达到4 MPa或最大主应变为0.003 3时，则材料失效，退出计算并删除单元。炸药采用*MAT_HIGH_EXPLOSIVE_BURN模型和*EOS_JWL状态方程，参数[11]见表3。空气层采用*MAT_NULL模型和*EOS_LINEAR_POLYNOMIAL状态方程，参数[11]见表4。

表1　梁钢筋模型材料参数

表2　混凝土模型材料参数

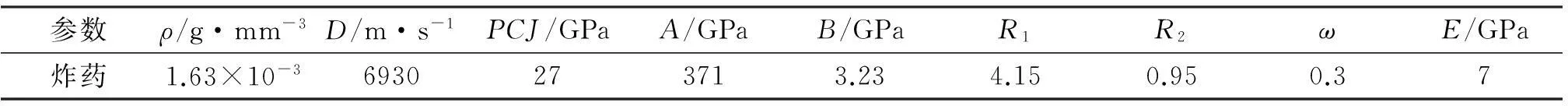
表3　炸药模型材料参数

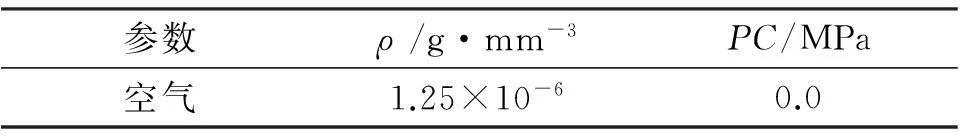
表4　空气模型材料参数

3结果分析

3.1破坏模式和损毁形态

爆炸荷载作用下，钢筋混凝土梁可能发生弯曲破坏、剪切破坏、弯剪破坏或冲剪破坏[10]。弯曲破坏通常表现为受拉区混凝土出现横向裂缝，钢筋屈服或拉断，受压区混凝土有压碎；剪切破坏通常表现为支座处或剪跨区出现较多明显的45°斜裂缝；弯剪破坏则有弯曲破坏和剪切破坏的共同特点；冲剪破坏通常表现为梁整体变形不明显，梁上混凝土成段剥落，钢筋裸露。炸药位于梁跨中(X=L/2)，不同炸药量W、不同炸高H条件下的计算结果如表5所示。从表5可以看出，当3种炸药量接触爆炸和13 kg炸药炸高为0.5 m时，该梁发生冲剪破坏，跨中混凝土大量剥离，钢筋全部裸露；当5.5 kg炸药炸高为0.5 m和13 kg炸药炸高为1 m时，该梁发生弯剪破坏，梁跨中受压区混凝土有压碎，受拉区出现裂缝，支座附近出现较多斜裂缝；当1.63 kg炸药炸高为0.5 m，5.5 kg炸药炸高为1 m和2 m，13 kg炸药炸高为2 m和4 m时，该梁发生弯曲破坏，梁跨中仅受拉区出现裂缝，支座附近有少量斜裂缝；在其余情况下，该梁均未发生破坏。

表5　梁的破坏模式和损毁形态(X=L/2)

3.2梁最大挠度

不同炸药量W、不同炸高H、不同炸点位置X条件下，梁最大挠度的计算结果如图2所示。从图2(a)可以看出当炸药位于梁跨中(X=L/2)时，在H不变的条件下，随着W的增加，即爆炸荷载作用增大，梁的最大挠度亦增大；在W不变的条件下，随着H的增加，即爆炸荷载作用减小，最大挠度也减小，且减小趋势随着炸药量的增加越发明显。规范[18]规定受弯构件的挠度限值为L/300，若超过该规范限值，认为该梁破坏，即本文计算模型中，W=1.63 kg的所有工况和W=13 kg时，H为2,4 m时，爆后跨中挠度均满足要求，未破坏。从图2(b)、图2(c)和图2(d)中可以看出，在W和H均相同的条件下，随着炸点位置X的增加(逐渐靠近跨中)，即爆炸荷载作用向跨中移动，最大挠度逐渐增大，这是因为荷载向跨中移动，梁上最大弯矩增大，变形和挠度亦增大；而随着H的增加，挠度增大的趋势逐渐减弱，即此时炸点位置X的影响可以忽略。

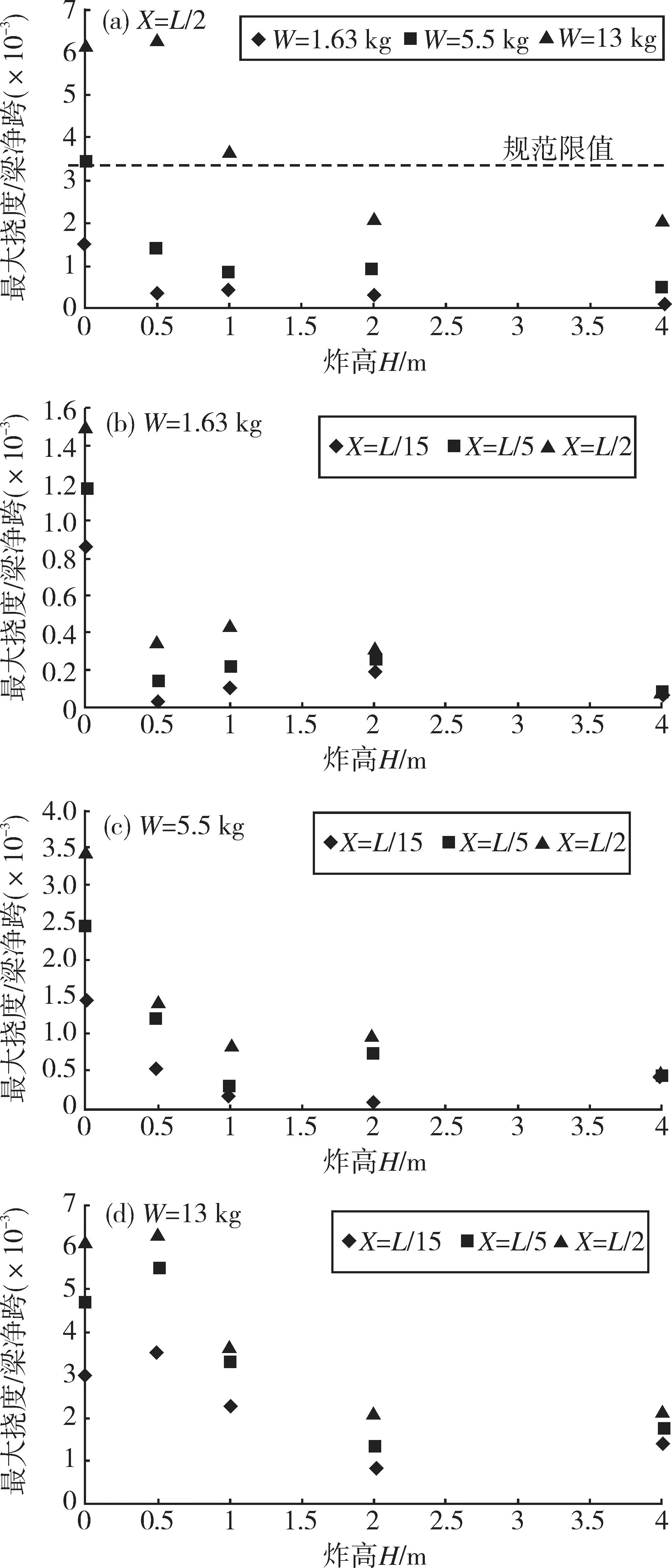
图2　梁的最大挠度

3.3爆后剩余承载力及生存能力

在爆炸计算结束后，仅保留梁在爆炸荷载作用下产生的变形和位移，建立梁的三点弯曲试验计算模型(如图3所示)。本文计算模型的挠度限值为22 mm(L/300)，其所对应的跨中竖向荷载值即为该梁的爆后剩余承载力Rf。当炸药量W为13 kg，炸高H为0.5，1，2，4 m时(考虑到接触爆炸时梁上混凝土剥落和露筋情况严重，认为梁已失效，此处不考虑H=0 m)，受损后梁的跨中竖向荷载Rf-跨中挠度曲线w如图4所示。经计算梁爆前设计承载力S=627 kN。由式(1)确定损伤度D值，根据D的临界值判定该梁的生存能力，是否可继续使用，是否需要修复加固。从表6可以看出，在W=1.63 kg的条件下，只有H=0.5 m时受损梁不可继续使用；而在W=13 kg的条件下，只有H=4 m时受损梁还可继续使用。此结果对照图2(a)可知，在爆炸荷载作用下，选取爆后剩余承载力作为损伤指标来评估其生存能力比选取跨中最大挠度更为合理。

图3　梁的爆后剩余承载力计算模型

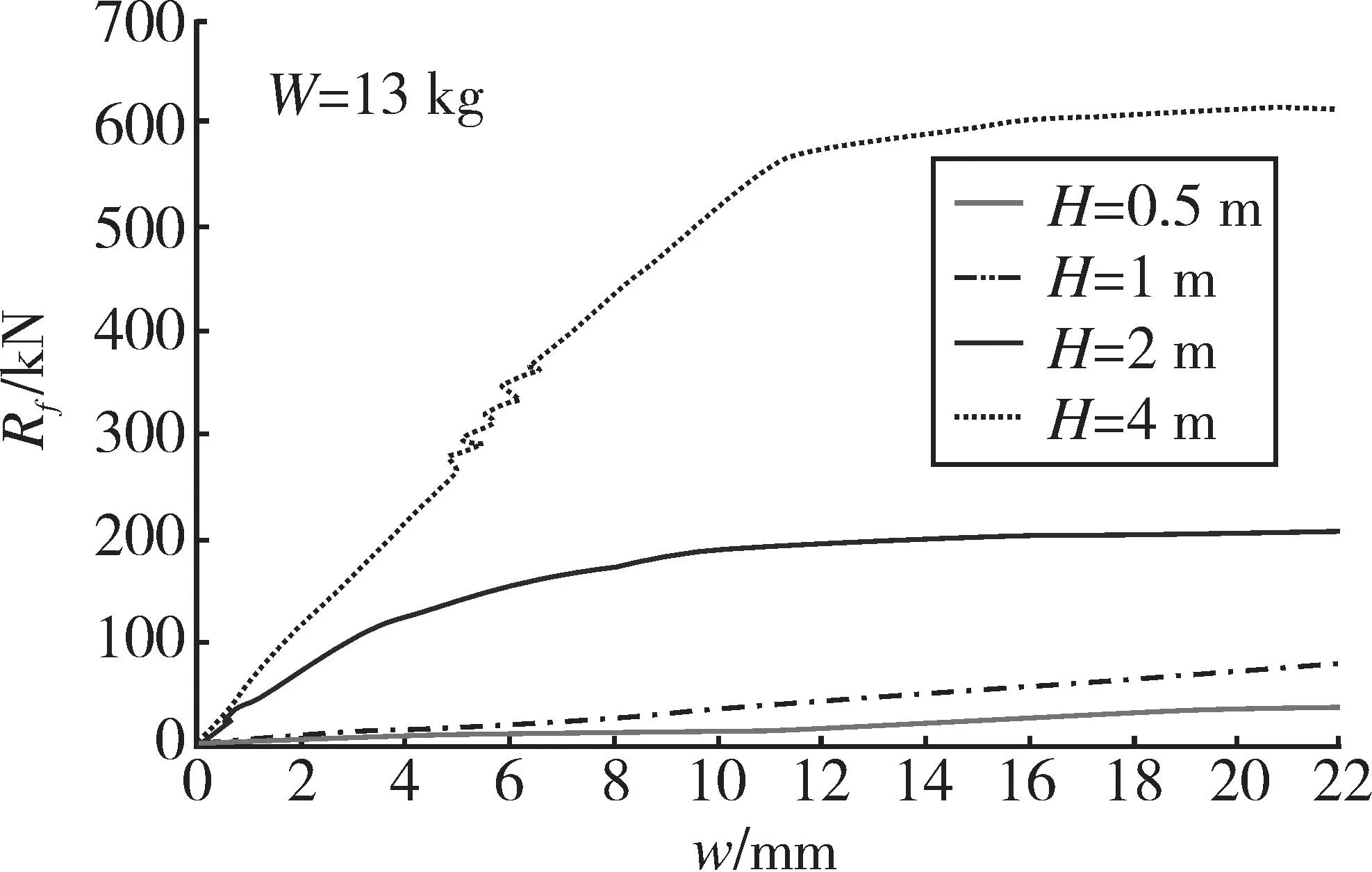
图4　Rf-w曲线

炸药量W/kg 1.63 13 炸高H/m0.51240.5124剩余承载力Rf/kN2546156276273979225610损伤度D0.590.02000.940.870.640.03生存能力需要拆除重建不必处理,继续使用不必处理,继续使用不必处理,继续使用需要拆除重建需要拆除重建需要拆除重建不必处理,继续使用

4小结

本文利用有限元软件ANSYS/LS-DYNA数值模拟分析了钢筋混凝土梁在爆炸荷载作用下的破坏模式和损毁形态，考虑炸药量、炸点高度和炸点位置的影响，得到其爆后剩余承载力和损伤度D值，并评估其生存能力。结果表明，以承载力的损失程度作为损伤指标来进行生存能力评估，以及确定钢筋混凝土梁爆后的处理方式(继续使用、修复加固后使用、拆除重建)是可行的，同时可为地面建筑结构抗爆防护研究与结构设计提供参考。

参考文献

[1]WU Ke-Chiang, LI Bing, TSAI Keh-Chyuan. The effects of explosive mass ratio on residual compressive capacity of contact last damaged composite columns[J]. Journal of Constructional Steel Research, 2011, (5):602-612.

[2]JAYASOORIYA Ruwan, THAMBIRATNAM D P, PERERA N J, et al. Blast and residual capacity analysis of reinforced concrete framed buildings[J]. Engineering Structures, 2011, 23: 3483-3495.

[3]匡志平，杨秋华，胡坚尉. 爆炸荷载作用下钢筋混凝土框架结构的动力响应研究[J]. 力学季刊, 2010，31(3)：443-447.

[4]师燕超. 爆炸荷载作用下钢筋混凝土结构的动态响应行为与损伤破坏机理[D]. 天津：天津大学博士学位论文, 2009.

[5]魏雪英，白国良. 爆炸荷载下钢筋混凝土柱的动力响应及破坏形态分析[J]. 解放军理工大学学报:自然科学版, 2007，8(5)：525-529.

[6]侯延利. 爆炸冲击荷载作用下钢筋混凝土柱的动态响应分析 [D]. 陕西西安：长安大学硕士学位论文， 2008.

[7]LUCCIONI B M, AMBROSINI R D, DANESI R F. Analysis of building collapse under blast loads[J]. Engineering Structures, 2004, (2): 63-71.

[8]柳锦春，方秦，龚自明，等. 爆炸荷载作用下钢筋混凝土梁的动力响应及破坏形态分析[J]. 爆炸与冲击, 2003，25(1)：25-30.

[9]焦延平，郭东，张虹，等. 爆炸荷载作用下钢筋混凝土梁非线性有限元分析[J]. 振动与冲击， 2003，22(3)：65-67.

[10] 师燕超，李忠献. 爆炸荷载作用下钢筋混凝土柱的动力响应与破坏模式[J]. 建筑结构学报， 2008，29(4)：112-117.

[11] 龚顺风，金伟良，何勇. 内部爆炸荷载作用下钢筋混凝土板的动力响应研究[J]. 振动工程学报， 2008，21(5):516-520.

[12] 李天华. 爆炸荷载下钢筋混凝土板的动态响应及损伤评估[D]. 陕西西安：长安大学博士学位论文, 2012.

[13] 李忠献，师燕超，史祥生. 爆炸荷载作用下钢筋混凝土板破坏评定方法[J]. 建筑结构学报, 2009，30(6):60-66.

[14] 汪明，爆炸荷载作用下钢结构损伤机理及砌体墙破碎过程研究[D]. 天津：天津大学博士学位论文， 2010.

[15] GB 50292-1999，民用建筑可靠性鉴定标准[S].

[16] JGJ_125-1999，危险房屋鉴定标准[S].

[17] GB/T 232-2010，金属材料弯曲试验方法[S].

[18] GB 50010-2010，混凝土结构设计规范[S].

[19] 过镇海，时旭东. 钢筋混凝土原理和分析[M]. 北京：清华大学出版社， 2003.

Viability Analysis and Numerical Calculation of Damaged Reinforced Concrete Beam

PENG Yun, FU Yu

(SchoolofCivilEngineeringandArchitecture,SouthwestUniversityofScienceandTechnology,Mianyang621010,Sichuan,China)

Abstract:In order to estimate the viability of reinforced concrete beams after blasting, determine the possibility of continued service, and control the quantities and cost of rehabilitation work, it was numerical simulated using finite element analysis software ANSYS/LS-DYNA. The failure mode and damage morphology of reinforced concrete beam were analyzed under different explosive charges, explosive heights and explosive positions. The residual capacity after blasting and the damage degree were calculated, and its viability was estimated. The results show the feasibility of estimating the viability of reinforced concrete beam after blasting by the damage degree of its flexure capacity. It also can provide the reference for anti-explosion protection analysis and structure design of building structures.

Key words:Reinforced concrete beam; Residual capacity after blasting; Viability after blasting; Numerical simulation

中图分类号：O383+.2

文献标志码：A

文章编号：1671-8755(2016)01-0030-05

作者简介:彭芸(1981—)，女，硕士，讲师，研究方向为结构分析与设计。E-mail:435671968@qq.com

基金项目:国防基础科研项目(B3120110004)；四川省教育厅资助项目(12ZA187)。

收稿日期：2015-04-16