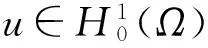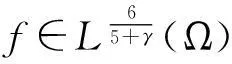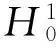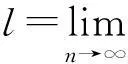一类奇异Kirchhoff型问题正解的存在性
2016-05-06廖家锋
廖家锋, 陈 明, 张 鹏
(遵义师范学院 数学与计算科学学院, 贵州 遵义 563002)
一类奇异Kirchhoff型问题正解的存在性
廖家锋,陈明,张鹏
(遵义师范学院 数学与计算科学学院, 贵州 遵义 563002)
摘要:Kirchhoff型问题通常被看作非局部问题,起源于非线性振动理论.研究一类奇异Kirchhoff型问题,利用变分方法,获得该问题正解的存在性.该结果丰富奇异Kirchhoff型问题正解的存在性理论.
关键词:Kirchhoff型问题; 奇异; 正解; 变分方法
考虑如下奇异Kirchhoff型问题
(1)

当a=1,b=0时,问题(1)退化到经典的奇异椭圆方程.这类问题正解的存在性以及多重性已有许多结果(如文献[1-9]).而关于奇异Kirchhoff型问题正解的存在性的结果相对就较少了(如文献[10-13]).文献[12]中研究了当λ=0,γ>1时问题(1)的正解存在性的充要条件.当3 定义Iλ为问题(1)对应的能量泛函,即 (2) 1主要结果 注记 1当a=0,b>0,问题(1)被称为退化的奇异Kirchhoff型方程.而当a=1,b=0时问题(1)退化到奇异椭圆方程,当0 定理1的证明分以下2步来证明定理1. 由Hölder不等式和Sobolev不等式,有如下不等式成立 (3) (4) 这里C1,C2>0为常数.从而根据(3)和(4)式有 (5) (7) 从而可得 (8) 这里o(1)是n→∞时的无穷小量.再结合(5)~(8)式可得 第2步证明u*是问题(1)的正解.事实上,根据第1步中Iλ(u*)=m<0,有u*≢0. 由中值定理可得 其中当θ→0+,η→0+时,对几乎所有的x∈Ω有 对所有的x∈Ω有(u*+θtφ)-γφ≥0,从而由Fatou引理可得 (10) 根据Lebesgue控制收敛定理可得 (11) (12) 因此,有∫Ω(u*,φ)dx≥0,从而根据强极大值原理可得u*>0在Ω几乎处处成立. (13) 参考文献 [1] GUI C F, LIN F H. Regularity of an elliptic problem with a singular nonlinearity[J]. Proc R Soc Edinb,1993,A123:1021-1029. [2] SUN Y J, WU S P, LONG Y M. Combined effects of singular and superlinear non-linearities in some singular boundary value problems[J]. J Diff Eqns,2001,176:511-531. [3] SUN Y J, WU S P. An exact estimate result for a class of singular equations with critical exponents[J]. J Funct Anal,2011,260:1257-1284. [4] BOCCARDO L. A Dirichlet problem with singular and supercritical nonlinearities[J]. Nonlinear Anal,2012,75:4436-4440. [5] DAVID A, BOCCARDO L. Multiplicity of solutions for a Dirichlet problem with a singular and a supercritical nonlinearities[J]. Diff Integ Eqns,2013,26:119-128. [6] DAVID A, LOURDES M M. Multiplicity of solutions for a Dirichlet problem with a strongly singular nonlinearity[J]. Nonlinear Anal,2014,95:281-291. [7] 廖家锋,马淑云. 一类奇异半线性椭圆问题的注记[J]. 四川师范大学学报(自然科学版),2012,35(3):335-339. [8] 廖家锋,张鹏. 一类奇异次线性椭圆问题基态解的存在性[J]. 四川师范大学学报(自然科学版),2015,38(6):867-870. [9] 廖家锋,张鹏. 一类奇异椭圆方程的共振问题[J]. 数学杂志(已接受). [10] LIU X, SUN Y J. Multiple positive solutions for Kirchhoff type problems with singularity[J]. Commun Pure Appl Anal,2013,12(2):721-733. [11] LEI C Y, LIAO J F, TANG C L. Multiple positive solutions for Kirchhoff type of problems with singularity and critical exponents[J]. J Math Anal Appl,2015,421:521-538. [12] 曹小强,孙义静. 一类奇异非线性Kirchhoff型问题的正解[J]. 中国科学院大学学报,2014,31(1):5-9. [13] LIAO J F, ZHANG P, LIU J, et al. Existence and multiplicity of positive solutions for a class of Kirchhoff type problems with singularity[J]. J Math Anal Appl,2015,430:1124-1148. [14] RUDIN W. Real and Complex Analysis[M]. New York:McGraw-Hill,1966. [15] WILLEM M. Minimax Theorems[M]. Boston:Birkhauser,1996. 2010 MSC:35B09 (编辑周俊) Existence of Positive Solutions for a Class of Singular Kirchhoff Type Problem LIAO Jiafeng,CHEN Ming,ZHANG Peng (SchoolofMathematicsandComputationalScience,ZunyiNormalCollege,Zunyi563002,Guizhou) Abstract:Kirchhoff type problems are often considered to as nonlocal and originate in the theory of nonlinear vibrations. A class of singular Kirchhoff type problems is discussed. By the variational methods, the existence of positive solutions is obtained. This result enriches the theory of positive solutions for Kirchhoff type problems. Key words:Kirchhoff type problem; singularity; positive solution; variational method doi:10.3969/j.issn.1001-8395.2016.01.018 中图分类号:O177.91 文献标志码:A 文章编号:1001-8395(2016)01-0103-04 作者简介:廖家锋(1983—),男,副教授,主要从事非线性分析方面的研究,E-mail:liaojiafeng@163.com 基金项目:贵州省科学技术科学基金(LKZS[2012]11、LKZS[2012]12和LKZS[2014]22) 收稿日期:2015-02-17