海流条件下中性缆缆形及张力的理论研究

邢 丹，马利斌

（中国船舶科学研究中心，江苏 无锡 214082）

海流条件下中性缆缆形及张力的理论研究

邢 丹，马利斌

（中国船舶科学研究中心，江苏 无锡 214082）

文章考虑缆绳经受的法向与切向流体阻力，在自然坐标系下推导了任意海流中缆绳的动力学方程。建立了中性缆在均匀、线性及组合海流作用下缆形与张力的参数表达式。参数表达式给出了对应海流作用下缆形及张力的物理规律，从而为参数迭代求解时迅速收敛指明了数学途径。自行编制程序，算例的定量结果进一步验证了其物理规律，也表明在长缆绳下，忽略切向阻力在工程上是不合适的。

中性缆；缆形；线性海流；参数表达

0 引 言

水下拖曳系统在水下资源勘探开发、地质考察、沉船打捞等活动中得到了广泛的应用。拖揽用于实现母船和设备之间的拖带与光电信号传输。对于拖揽，其缆长、缆形及张力分布的精确确定，在工程设计及应用上有着重要的意义。拖曳系统实验室试验研究受各种条件限制，很难全尺度进行，目前只有少量的海上试验数据公布可见[1]。近些年来数值仿真得到了广泛的应用，发展了集中质量法、有限元法、有限差分法和直接积分法等拖揽水动力模型。上世纪开始，就有学者开始了飞机拖揽、水下拖曳等系统中缆索二维缆形的解析分析。解析解需要进行一系列的假设与简化，但其结果却可给出规律性的结论并对数值仿真结果予以验证。1976年，Simpson和Tabarrok[2]推导了漂浮在水平面内的中性缆在均匀海流作用下的平衡方程，证明了在不计切向流体阻力的情况下，平衡缆形为悬链线，张力为恒值。切向流体阻力引起的悬链线的偏移由一阶扰动理论近似给出，切向流体阻力采用了正比于切向速度分量的形式。1994年，Dennis[3]对Simpson和Tabarrok的工作做了补充。1995年，Leech和Tabarrok[4]忽略了拖揽的切向阻力，推导了均匀海流作用下二维稳态控制方程，得到了缆形和张力的半解析表达，研究了拖揽的稳态空间形状和张力分布。2013年，章浩燕[5]对Leech和Tabarrok的二维解予以了补充。

对于速度与拖揽之间夹角较小的系统，忽略切向阻力或者将其取为定值并不适合。本文考虑切向与法向阻力，推导了海流中缆绳的二维动力学方程。建立了中性缆在均匀海流、线性变化海流与组合海流作用下的空间位形与张力分布的参数表达式。得到了在不同海流作用下缆形及张力的物理规律并自行编制程序，计算了经典算例。

1 受力分析与控制方程

忽略缆索刚度，缆索和拖体在同一平面。如图1建立大地坐标系为三个方向上的单位坐标矢量，x向与海流方向相同，y向为海水深度增加方向，z向满足右手定则，整个缆绳便在xoy平面内。在缆绳上建立自然坐标为缆绳切向量，指向缆长增加方向，法向量

记θ为缆绳与y轴的夹角。则

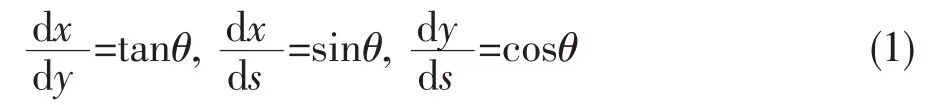
将缆索看作圆柱体，海流法向阻力系数Cn和切向阻力系数Ct由拖揽特性根据经验或试验数据取为定值。经ds，张力由T变为T+dT，倾角θ变为θ+dθ，则力平衡方程为：

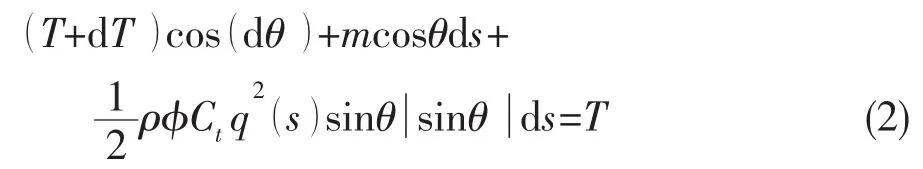
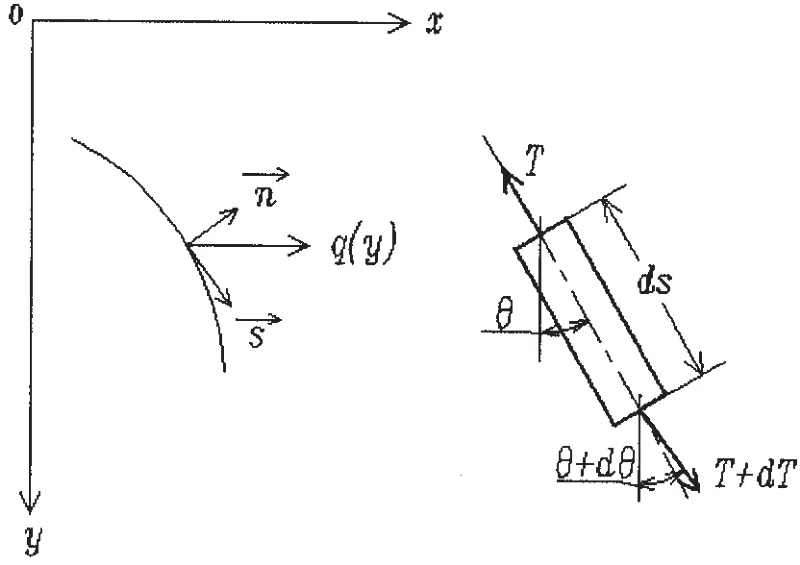
图1 坐标系及受力分析Fig.1 Coordinate system and force analysis

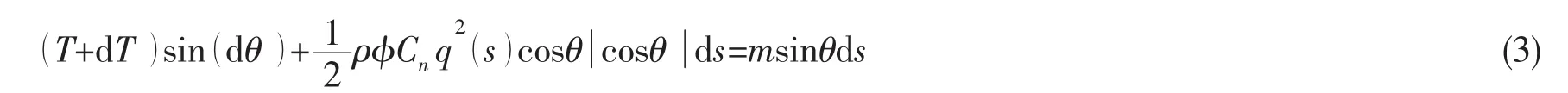
其中：m为单位长度拖揽在水中扣去浮力后的重量，ρ为海水密度，φ为缆绳直径，q为海流大小。略去二阶小量，可得

1.1 中性缆、均匀流

（6）、（7）两式相除

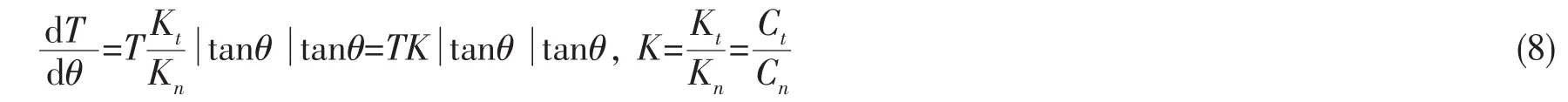
积分可得

由（1）、（7）和（9）式可得：

1.2 中性缆，线性变化海流

此时，（4）、（5）式退化成：

（16）、（17）两式相除并积分，可得与均匀流相同的张力表达式（9）。

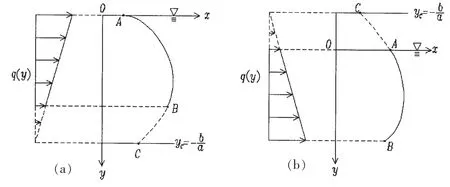
图2 线性变化海流Fig.2 Linear changing current flow

为数学求解方便，将海流场及缆绳拓展到全平面xoy，如图2所示。在xoy全平面，（16）和（17）式依然成立，其物理解在y≥0。记并有dq=ady，注意到广义缆绳与直线交于C点式变为整理可得：

对（18）式积分并代入C点边值，可得：

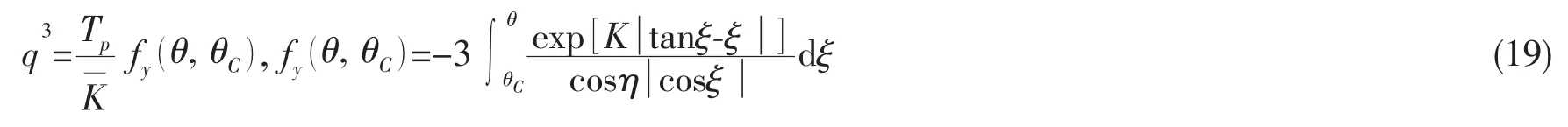
至此推导出了线性变化海流下缆形及张力表达式，通过C点的引入，得到了与均匀流（9）、（13）、（14）和（15）式形式相似的参数表达。

1.3 恒流、线性流的组合分布

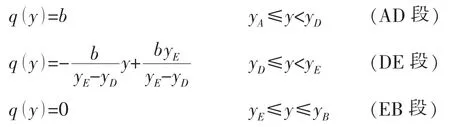
在AD段：T，y，x，s即为均匀海流中（9），（13），（14），（15）式，其中Tp，fx，fy，fs均加下标AD即可。

在DE段：T，y，x，s即为线性变化海流中（9），（20），（21），（22）式，其中Tp，fx，fy，fs均加下标DE即可。

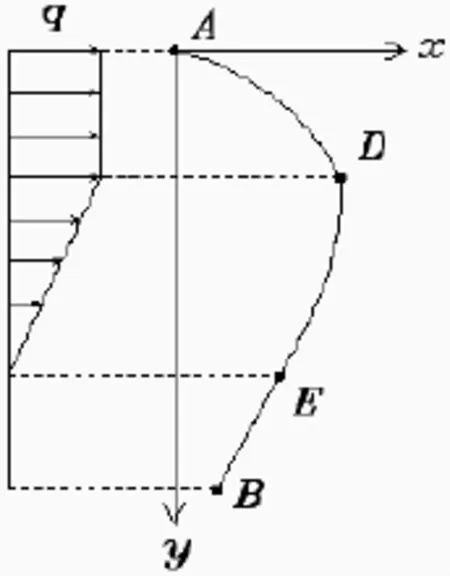
图3 组合海流Fig.3 Combined current

2 拖缆动力学规律分析

2.1 中性缆，x向均匀流

2.1.1 缆形变化规律

由（9）、（13）、（14）和（15）式可以看出，对于任意中性缆及均匀流，若K相同，则fT，fx，fy，fs完全相同。那么其对应的无量纲张力无量纲型值及无量纲缆长均相等，即缆形在无量纲平面内为同一条曲线。

（b）缆形是向海流正向突出的，且是关于y=yp的对称曲线

由（13）、（15）式，当s-sp→∞，对于定值y-yp有仅当时才有

2.1.2 张力变化规律

（a）型线极值点对应的张力为全缆最小值，向端点靠拢，张力增加；若Ct=0，则张力为常数Tp。此由（9）式可得。

（b）当缆绳长度增加时，相应的张力Tp减小

由2.1.1（d），当s-sp→∞时根据（13）式此时而是定值，故唯有L1→0，即Tp→0。

（c）当缆绳收紧时，相应张力增加

（d）Tp与流速的平方成正比

由2.1.1（e），不同流速时缆形不变。那么x-xp、y-yp、s-sp均不变，则亦不变，即

2.2 中性缆，线性流

2.2.1 缆形变化规律（a）缆形总体上是海流正方向突出的，且不对称

由 （20）、（22）式当s-sC→∞，对于定值y-yC有仅当时才有

2.2.2 张力变化规律

（a）同2.1.2（a），型线极值点对应的张力为全缆最小值，向端点靠拢，张力增加；若Ct=0，则张力为常数Tp。

（b）当缆绳长度增加时，相应的张力Tp减小

由2.2.1（c）当s-sC→∞时由（13）式知此时而是定值，故唯有L2→0，即Tp→0。

（c）当缆绳收紧时，相应的张力增加

2.3 恒流、线性流的组合分布

3 编程求解逻辑

传统的微分方程求解，以完整的边界条件为求解起点。缆绳动力学微分方程求解起始点应该有四个边值已知。但实际问题往往只有其中两个已知，另外两个已知边值在其解的末端点。这给求解过程带来不小的困难，即使是本文的参数表达式，也无法避开此难处。但第2章中缆的特性及规律使我们以数值积分办法对θ,T全域搜索时变得极有方向性，从而可以快速求解。

分段海流时，只需将均匀海流与线性变化海流的缆求解结合，在连接点处张力相等，θ相同，采用类似的逼近逻辑便可方便求解。本文在个人电脑上采用Fortran语言编程，即使积分步长取得很小，如Δθ=0.000 1 rad，均匀海流和线性变化海流均可在数秒内得到结果，分段海流大概需要十几秒即可收敛。

4 计算结果与讨论

4.1 缆长的影响

计算了缆长为250、300、350、400m时的缆形及张力分布，计算参数如表1（a）所示。由图4（a）可知不同缆长时拖揽空间形状相似。张力分布如图4（b）所示，张力在θ=0时最小，系缆点处最大。张力随缆长的增加而减小，但趋势减缓。缆长300 m、350 m、400 m时的最大张力分别是缆长250 m时最大张力的75%、65%、60%，见表2。

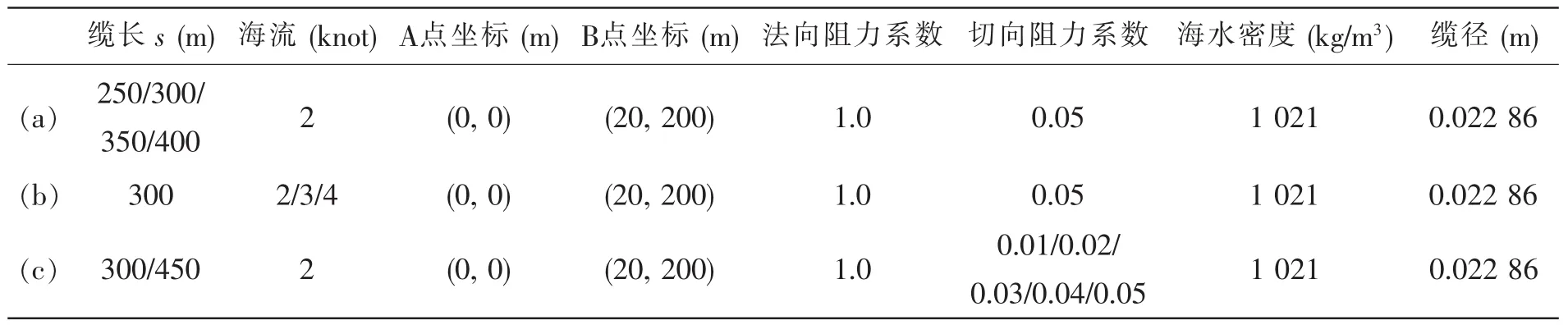
表1 计算参数Tab.1 Calculation parameters

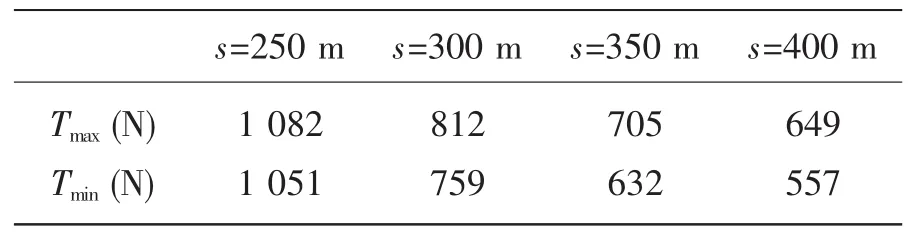
表2 不同缆长时最大及最小张力Tab.2 Maximum&minimum tension of different cable length

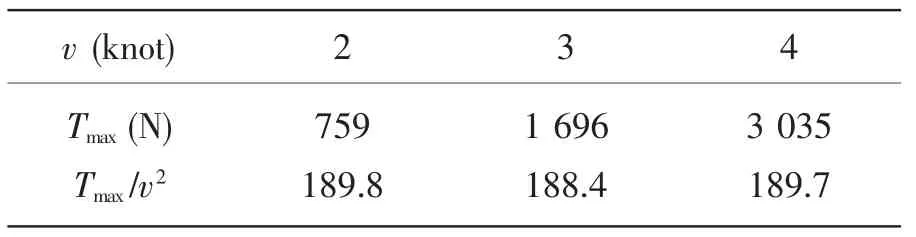
表3 最大张力与海流大小关系Tab.3 Relationship between maximum tension and current velocity

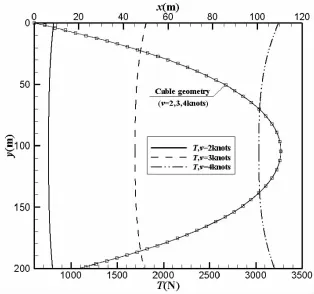
图5 不同海流大小时缆形及张力分布Fig.5 Cable geometry and tension distribution in different current velocity

4.2 海流大小的影响

图5给出了表1（b）所示参数下，不同海流大小时的缆形与张力。可知缆形与海流大小无关，但张力随海流增大而迅速增大。由表3可知最大张力与海流大小的平方成正比关系。

4.3 切向阻力系数的影响

文献[4-5]忽略了切向阻力的影响，本文分别计算了缆长为300 m、450 m两种情况下不同切向阻力系数时的缆形及张力分布。具体计算参数如表1（c）所示。由图6所示结果可以看出，切向阻力系数变化时缆形几乎不变，但对拖揽内部张力大小及分布有所影响。在缆长s=300 m情况下，不考虑切向阻力即Ct=0.0时，缆绳张力为恒值766 N；Ct=0.02时，最大张力增大到102.5%；Ct增大到0.06时，最大张力增大到107.4%。缆长s=450 m情况下，不考虑切向阻力时，缆绳张力为恒值521 N；Ct=0.02时，最大张力增大到107.3%；Ct增大到0.06时，最大张力增大到122%。缆长增大时切向阻力的影响变大。在计算时应该根据缆绳形状选择合适的阻力系数，或进行试验测定，以便得到更好的预报结果。

4.4 不同海流形式的影响

计算了三组不同海流作用下的缆形及张力分布。

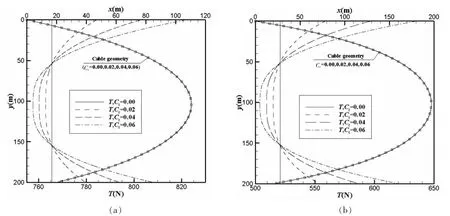
图6 不同切向阻力时缆形及张力分布 （a）s=300 m；（b）s=450 mFig.6 Cable geometry and tension distribution in different tangential resistance(a)s=300 m;(b)s=450 m

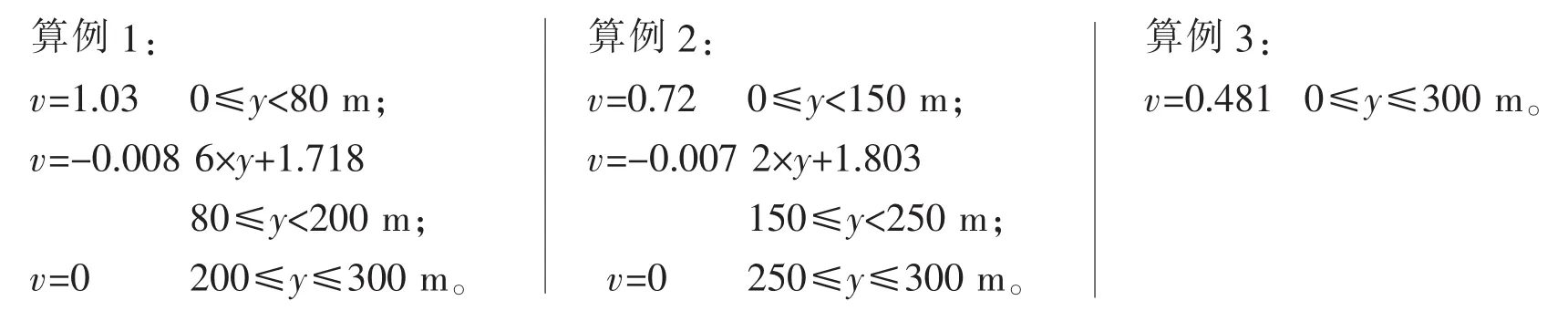
其余参数均相同，A（0，0），B（50，300），缆长s=350 m，法向阻力系数Cn=1.0，切向阻力系数Ct= 0.05，海水密度ρ=1 021 kg/m3，缆径φ=0.022 86 m。

在这三个算例中，平均速度相同，均为0.481 m/s。图7给出了不同海流形式下的缆形及张力分布。可见即使平均速度相同，在不同的海流模型作用下，拖揽的空间位形，张力分布均有明显的变化，算例1的最大张力为算例3的两倍。故计入不同海流形式的影响可更准确地预报实际情况。

图7 （a）不同海流形式时缆形；（b）不同海流形式时张力分布Fig.7(a)Cable geometry;(b)Tension distribution in different current types

5 结 论

本文在自然坐标系下，推导了任意海流中缆绳的动力学方程，并针对均匀流及线性流建立了缆形及张力分布的参数表达式。常规的真实海流可视为两者的组合。对这些参数表达式的分析，一方面得到了均匀流、线性流及二者组合的流剖面下缆形及张力的物理规律；另一方面也指出了参数表达式积分求解时，在θ,T全域迅速迭代收敛的数学途径。自行编制的数值程序在个人电脑上耗费几秒至十几秒完成了均匀流、线性流及组合流的典型算例，给出了定量结果，进一步验证了其物理规律。计算结果还表明切向阻力系数对拖揽张力的影响随着拖揽长度的增加而增大，在工程上应予以考虑。

[1]Rispin P.Data package No.1 for cable and array maneuvering[R]．Bethesda,Maryland,USA:David W.Taylor Naval Ship Research and Development Center,1980.

[2]Simpson A,Tabarrok B．On the equilibrium configuration of a chain subjected to uniform fluid flow in a horizontal plane[J]. International Journal of Mechanical Sciences,1976,18(2):91-94.

[3]Dennis N.On the formation of funicular curves[J].International Journal of Mechanical Sciences,1994,36(3):183-188.

[4]Leech C M,Tabarrok B．The cable geometry for a towed submersible[J]．International Journal of Mechanical Sciences,1995, 37(10):1079-1087.

[5]章浩燕,朱克强,张 洋,等.水下拖曳缆索二维几何形态的研究[J].舰船科学技术,2013,35(4):35-39. Zhang Haoyan,Zhu Keqiang,Zhang Yang,et al.Research on the two-dimensional cable geometries of a towed submersible [J].Ship Science and Technology,2013,35(4):35-39.

Theoretical study on the cable geometry and tension of neutral cable in current

XING Dan,MA Li-bin
(China Ship Scientific Research Center,Wuxi 214082,China)

The dynamic equations of the cable in different ocean currents are developed in the natural coordinate,the effects of normal and tangential components of the fluid drag are both considered.The parameter expressions for the cable geometry and tension of the neutral cable under the action of uniform,linear and combined current flow are established.The physical laws of the cable geometry and tension distribution in different currents are obtained.Also,the mathematical approach to the fast convergence of the numerical integration is pointed out.Some typical examples are calculated by the self-compiled program.The quantitative results further verify the physical laws,and show that ignoring tangential resistance is not appropriate for long cable.

neutral cable;cable geometry;linear current;parameter expression

U661.1

A

10.3969/j.issn.1007-7294.2016.08.007

1007-7294（2016）08-0983-09

2016-06-26

海洋调查专项（TRQDC201401）

邢 丹（1987-），女，硕士，工程师，E-mail:xingdan0420@163.com。